Вступление
В этой небольшой статье я расскажу о теории категорий в контексте системы типов языка Haskell. Никакой зауми, никаких уловок – постараюсь объяснять всё наглядно. Я хочу показать тесную связь языка программирования с математикой, чтобы спровоцировать у читателя осознание одного, через другое и наоборот.
Не хотелось бы повторять перевод на эту тему, который уже был на хабре: Монады с точки зрения теории категорий, но для целостности статьи, я всё же буду давать основные определения. При этом, в отличие от той статьи, я не хочу делать основной упор на математику.
Эта статья во многом повторяет (в том числе заимствует иллюстрации) раздел из английской Haskell Wikibook, но тем не менее не является непосредственным переводом.
Что такое категория?
Примеры
Для наглядности рассмотрим сначала пару картинок изображающих простые категории. На них есть красные кружочки и стрелки:
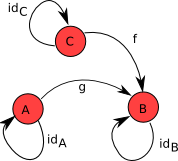

Красные кружочки изображают «объекты», а стрелки – «морфизмы».
Я хочу привести один наглядный пример из реальной жизни, который даст какое-то интуитивное представление о природе объектов и морфизмов:
Можно считать города «объектами», а перемещения между городами – «морфизмами». Например, можно представить себе карту авиарейсов (как-то не нашёл я удачную картинку) или карту железных дорог – они будут похожи на картинки выше, только сложнее. Следует обратить внимание на два момента, которые кажутся в реальности само собой разумеющимися, но для дальнейшего имеют важное значение:
- Бывает, что из одного города в другой никак не попасть поездом или самолётом – между этими городами нет морфизмов.
- Если мы перемещаемся в пределах одного и того же города, то это тоже морфизм – мы как бы путешествуем из города в него же.
- Если из Санкт-Петербурга есть поезд до Москвы, а из Москвы есть авиарейс в Амстердам, то мы можем купить билет на поезд и билет на самолёт, “скомбинировать” их и таким образом попасть из Санкт-Петербурга в Амстердам – то есть можно на нашей карте нарисовать стрелку от Санкт-Петербурга до Амстердама изображающую этот скомбинированный морфизм.
Определение
Итак, мы уже знаем, что категория состоит из объектов и морфизмов:
- Имеется класс (совокупность) объектов. Объектами могут быть любые сущности.
- Для любых двух объектов
AиBопределён класс морфизмовHom(A,B). Для морфизмаfиз этого класса объектAназывается областью, аB– кообластью. Это записывают так:
f ∈ Hom(A,B)илиf : A → B. - Для любых двух морфизмов
f : A → Bиg : B → Cопределена их композиция – морфизмh = g ∘ f,
h : A → C. Важно, что областьgи кообластьfсовпадают. - Композиция ассоциативна, то есть для любых морфизмов
f : A → B,g : B → Cиh : C → Dвыполнено равенство
(h ∘ g) ∘ f = h ∘ (g ∘ f) - Для любого объекта
Aимеется «единичный» морфизм, который обозначаетсяidA: A → Aи он нейтрален относительно композиции, то есть для любого морфизмаf : A → Bвыполнено:
idB∘ f = f = f ∘ idA.
id, поскольку его область/кообласть восстанавливаются из контекста.Можно проверить, что для приведённых выше примеров все свойства выполнены: композиция когда нужно определена, ассоциативна и соответствующие единичные морфизмы нейтральны относительно неё. Единственная неувязка возникает с ассоциативностью в примере про перемещения между городами – тут нужно думать о композиции, как “комбинировании билетов”, а не просто последовательных перемещениях конкретного человека.
Упражнение для самопроверки: проверить, изображает ли следующая картинка категорию

Категория Hask
А теперь главный пример, основная тема статьи. Категория Hask состоит из типов языка Haskell и функций между ними. Более строго:
- Объекты Hask: типы данных с кайндом1
*. Например, примитивные типы:Integer,Bool,Charи т.п. “Тип”Maybeимеет кайнд* → *, но типMaybe Boolимеет кайнд*и поэтому является объектом в Hask. То же самое с любыми параметризованными типами, но о них позже. Обозначение:a ∷ *≡ “типaимеет кайнд*” ≡ “aявляется объектом в Hask”. - Морфизмы Hask: любые Haskell’евские функции из одного объекта (типа) в другой. Если
a, b ∷ *, то функцияf ∷ a → b– морфизм с областьюaи кообластьюb. Таким образом класс морфизмов между объектамиaиb– обозначается типомa → b. Для полноты аналогии с математической нотацией можно ввести такой синоним:
Но я не буду им дальше пользоваться, так как стрелка, на мой взгляд, нагляднее.type Hom(a,b) = a → b - Композиция: стандартная функция
(.) ∷ (b → c) → (a → b) → (a → c). Для любых двух функцийf ∷ a → bиg ∷ b → cкомпозицияg . f ∷ a → cопределяется естественным образом:
g . f = λx → g (f x) - Из этого определения очевидна ассоциативность композиции: Для любых трёх функций
f ∷ a → b,g ∷ b → cиh ∷ c → dвыполнено
Непосредственная проверка:(h . g) . f ≡ h . (g . f) ≡ λx → h (g (f x))(h . g) . f ≡ λx → (h . g) (f x) ≡ λx → (λy → h (g y)) (f x) ≡ λx → h (g (f x)) h . (g . f) ≡ λx → h ((g . f) x) ≡ λx → h ((λy → g (f y)) x) ≡ λx → h (g (f x)) - Для любого типа
a ∷ *функцияid ∷ a → aопределена тоже естественным образом:
Из этого определения очевидно выполнение требуемых свойств. Пустьid = λx → xf ∷ a → b
f . id ≡ λx → f (id x) ≡ λx → f x ≡ f id . f ≡ λx → id (f x) ≡ λx → f x ≡ f
Char это будет мономорфная функция id ∷ Char → Char. Поэтому я и говорил до этого про индекс – в Haskell’е можно не писать каждый раз какой именно id нам нужен, потому что его тип автоматически выводится из контекста.Итак, как мы видим, все требуемые сущности присутствуют, их взаимосвязи предъявлены и требуемые свойства выполняются, так что Hask – это полноценная категория. Обратите внимание на то, как все понятия и конструкции переносятся из математической нотации в Haskell с минимальными синтаксическими изменениями.
Дальше я расскажу о том, что такое функторы и как они воплощаются в категории Hask.
Функторы
Функторы – это преобразования из одной категории в другую. Поскольку каждая категория состоит из объектов и морфизмов, то и функтор должен состоять из пары отображений: одно будет сопоставлять объектам из первой категории объекты во второй, а другое будет сопоставлять морфизмам из первой категории – морфизмы во второй.
Сначала я дам математическое определение, а потом продемонстрирую, насколько простым оно становится в случае Haskell’а.
Математическое определение
Рассмотри две категории
C и D и функтор F из C в D. Обозначения используются такие же как для морфизмов, только функтор обозначается большой буквой: F : C → D. Это F выполняет две роли:- Каждому объекту
Aиз категорииCставится в соответствие объект из категорииDи обозначаетсяF(A). - Каждому морфизму
g : A → Bиз категорииCставится в соответствие морфизм из категорииDи обозначаетсяF(g) : F(A) → F(B).
A ↦ F(A)
g : A → B ↦ F(g) : F(A) → F(B)
На картинке первое отображение изображено жёлтыми пунктирными стрелками, а второе – синими:
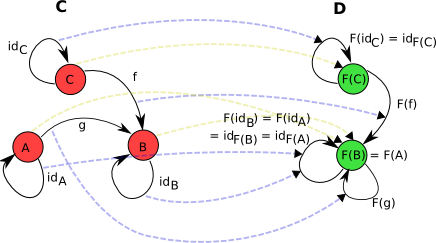
От функтора требуется выполнение двух вполне естественных требований:
- Он должен переводить каждый единичный морфизм данного объекта в единичный морфизм его образа:
F(idA) = idF(A) - Он должен переводить композицию морфизмов в композицию их образов:
F(h ∘ g) = F(h) ∘ F(g)
Функторы в Hask
Теперь мы рассмотрим функторы из категории Hask в Hask. К слову, такие функторы, которые переводят категорию в неё же саму, называются эндофункторами.
Так вот, значит нам нужно переводить типы в типы, а функции в функции – два отображения. И какая же конструкция языка Haskell воплощает первое? Правильно, типы с кайндом
* → *.Например, упомянутый уже тип
Maybe ∷ * → *. Это отображение, которое сопоставляет любому объекту a ∷ * объект из той же категории (Maybe a) ∷ *. Здесь Maybe a следует воспринимать не как конструктор параметризованного типа с данным параметром a, а как единый символ, аналогично F(A) из математического определения.Итак, первое отображение достаётся нам даром – это любой конструктор типа с параметром.
data Maybe a = Nothing
| Just a
Но как получить второе отображение? Для этого в Haskell определён специальный класс:
class Functor f where
fmap ∷ (a → b) → (f a → f b)
f ∷ * → *. То есть fmap – это полиморфная функция, которая принимает морфизм a → b, а возвращает морфизм f a → f b. Исходя из этого сделаем Maybe настоящим функтором, определив для него такую функцию: instance Functor Maybe where
fmap g = fg
where fg Nothing = Nothing
fg (Just x) = Just (g x)
Итак, мы получили два отображения:
a ∷ * ↦ Maybe a ∷ *
g ∷ a → b ↦ fmap g ∷ Maybe a → Maybe b
Ничего, что в отличие от математической нотации, они имеют разные имена, просто такова специфика языка, на смысл же это никак не влияет.
Хорошо, а что с выполнением требований?
fmap должен сохранять id и переводить композицию в композицию: fmap id ≡ id
fmap (h . g) ≡ (fmap h) . (fmap g)
Несложно проверить, это в случае приведённого выше определения
fmap для Maybe.Обратите внимание на то, что первое отображение мы получаем, просто объявив конструктор типа с параметром. И для него, как для отображения между объектами не важно, как устроен тип
Maybe: он просто сопоставляет объекту a объект Maybe a, что бы за этим ни стояло.В случае же с отображением морфизмов всё не так просто: нам приходится вручную определять
fmap, учитывая структуру типа Maybe. С одной стороны это даёт нам определённую гибкость – мы сами решаем, как какая-либо функция будет преобразовывать конкретную структуру данных. Но с другой стороны, было бы удобно получать это определение даром, если мы хотим, чтобы оно было устроенно естественным образом. Например, для типа data Foo a = Bar a Int [a]
| Buz Char Bool
| Qux (Maybe a)
g ∷ a → b должна рекурсивно обойти все конструкторы данных и везде, где у них есть параметр типа a преобразовать его с помощью g. Причём если встречается [a] или Maybe a, то для них должен сработать свой fmap g, который снова обойдёт их структуру и преобразует её.И о чудо, это возможно! В GHC есть соответствующее расширение. Пишем в коде:
{-# LANGUAGE DeriveFunctor #-}
…
data Foo a = …
deriving Functor
И получаем сразу полноценный эндофунктор категории Hask –
Foo, с соответствующим fmap.Кстати, стоит сказать, что эти функторы на самом деле отображают категорию Hask в её подкатегорию, то есть в категорию, с меньшим классом объектов и морфизмов. Например, отображением
a ↦ Maybe a мы никак не сможем получить простой тип Int – какое бы a мы ни взяли. Тем не менее получающийся подкласс объектов и класс функций на них в качестве морфизмов тоже образуют категорию.В документации класса Functor можно посмотреть ещё список типов, для которых исходно определено воплощение. Но они в основном делаются для того, чтобы потом сказать, что этот тип является монадой.
Заключение
Итак, я рассказал о категории Hask и о функторах в ней, и надеюсь, это помогло осознать систему типов Haskell в новом ракурсе. Возможно это кажется бесполезным с практической точки зрения, поскольку смысл
fmap все наверное понимают по-своему и без знания того, что такое функтор. Но дальше я собираюсь написать о естественных преобразованиях, монадах и других категорных конструкциях в ключе категории Hask и тогда уже, думаю, математические аналогии окажутся более полезными, позволяя лучше понять внутреннюю природу этих конструкций языка и применять их в дальнейшем более осознанно.- Если кто не встречался раньше с кайндами (kinds), я в двух словах поясню. Кайнды – это что-то вроде системы типов над обычными типами. Кайнды бывают двух видов:
*– это кайнд простого, не параметризованного типа. НапримерBool,Charи т.п. Пользовательский типdata Foo = Bar | Buz (Maybe Foo) | Quux [Int]тоже будет простым:Foo ∷ *, потому что конструктор типа не имеет параметров (хотя его конструкторы данных имеют)… → …– это более сложный кайнд, у него на местах троеточий могут стоять любые другие кайнды составленные из*и→. Например:[] ∷ * → *, или(,) ∷ * → (* → *)или что угодно ещё более сложное:((* → *) → *) → (* → *).
Смысл всё это имеет простой: конструкторы типов – это своего рода функции над типами и кайнды описывают, как эти функции правильно взаимодействуют. Например мы не можем написать[Maybe], потому что[] ∷ * → *, то есть аргумент скобочек должен иметь кайнд*, а уMaybeон* → *, то естьMaybeтоже функция и если мы дадим ей аргументInt ∷ *, то получимMaybe Int ∷ *и уже можем передать это скобочкам:[Maybe Int] ∷ *. Для такого рода контроля кайнды и существуют.