И снова здравствуйте! Сегодня я поведаю о фильтре Блума — структуре данных гениальной в своей простоте. По сути, этот фильтр реализует вероятностное множество всего с двумя операциями: добавление элемента к множеству и проверка принадлежности элемента множеству. Множество вероятностное потому, что последняя операция на вопрос «принадлежит ли этот элемент множеству?» даёт ответ не в форме «да/нет», а в форме «возможно/нет».
Как я уже говорил, идея до гениальности проста. Заводится массив битов фиксированного размера
Для проверки принадлежности, как вы уже догадались, достаточно посчитать значения хеш-функций для потенциального члена и убедиться, что все соответствующие биты установлены в единицу — это и будет ответом «возможно». Если же хотя бы один бит не равен единице, значит множество этого элемента не содержит — ответ «нет», элемент отфильтрован.
Код на JavaScript, просто потому что на Хабре он понятен многим. Прежде всего, нам нужно как-то представить битовый массив:
Так же, нам понадобится параметризированное семейство хеш-функций, чтобы было проще создавать
Ну и собственно, сам фильтр Блума:
Пример использования:
После игр с параметрами, становится понятно, что для них должны быть какие-то оптимальные значения.
Конечно, теоритические оптимальные значения я сам не выводил, просто сходил на Википедию, но и без неё, включив логику, можно прикинуть и уловить некоторые закономерности. Например, нет смысла использовать большой битовый массив, если вы собираетесь хранить там два значения, обратное тоже верно, иначе массив будет перенаселён, что приведёт к росту ошибочных ответов «возможно». Оптимальный размер массива в битах:
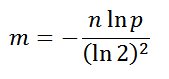
, где
Количество хеш-функций должно быть не большим, но и не маленьким. Оптимальное количество:

Применим полученные знания:
Например, Гуголь использует фильтры Блума в своей BigTable для уменьшения обращений к диску. Оно и не удивительно, ведь по сути, BigTable — это большая очень разреженная многомерная таблица, поэтому большая часть ключей указывает в пустоту. К тому же, данные распиливаются на относительно небольшие блоки-файлы, каждый из которых опрашивается при запросах, хотя может не содержать требуемых данных.
В данном случае, выгодно потратить немного оперативной памяти и сильно уменьшить использование диска. Скажем, чтобы уменьшить нагрузку в 10 раз, необходимо хранить примерно 5 бит информации на каждый ключ. Чтобы уменьшить в 100 раз, нужно порядка 10 бит на ключ. Выводы делайте сами.
Судя по тестам, оптимальные значения параметров для практики несколько завышены, можно смело понижать порог ложного срабатывания на порядок-два. Только обязательно протестируйте, если будете использовать — возможно, в моих тестах подобралась какая-то уникальная комбинация данных и хеш-функций или я банально где-то ошибся.
Очевидно, что удалять элементы из фильтра невозможно, но это просто решается — достаточно заменить битовый массив на массив счётчиков — инкрементировать при добавлении, декрементировать при удалении. Расход памяти, естественно, возрастает.
Так же очевидно, что невозможно динамически изменять параметры фильтра. Проблема элегантно решается введением иерархии фильтров, каждый последующий более точен, при необходимости иерархия растёт вглубь.
Пожалуй, на этом всё. Пока.
Как фильтр это делает?
Как я уже говорил, идея до гениальности проста. Заводится массив битов фиксированного размера
m и набор из k различных хеш-функций, выдающих значения от 0 до m - 1. При необходимости добавить элемент к множеству, для элемента считается значение каждой хеш-функции и в массиве устанавливаются биты с соответствующими индексами.Для проверки принадлежности, как вы уже догадались, достаточно посчитать значения хеш-функций для потенциального члена и убедиться, что все соответствующие биты установлены в единицу — это и будет ответом «возможно». Если же хотя бы один бит не равен единице, значит множество этого элемента не содержит — ответ «нет», элемент отфильтрован.
Реализация
Код на JavaScript, просто потому что на Хабре он понятен многим. Прежде всего, нам нужно как-то представить битовый массив:
function Bits()
{
var bits = [];
function test(index)
{
return (bits[Math.floor(index / 32)] >>> (index % 32)) & 1;
}
function set(index)
{
bits[Math.floor(index / 32)] |= 1 << (index % 32);
}
return {test: test, set: set};
}Так же, нам понадобится параметризированное семейство хеш-функций, чтобы было проще создавать
k различных. Реализация простая, но работает на удивление хорошо:function Hash()
{
var seed = Math.floor(Math.random() * 32) + 32;
return function (string)
{
var result = 1;
for (var i = 0; i < string.length; ++i)
result = (seed * result + string.charCodeAt(i)) & 0xFFFFFFFF;
return result;
};
}Ну и собственно, сам фильтр Блума:
function Bloom(size, functions)
{
var bits = Bits();
function add(string)
{
for (var i = 0; i < functions.length; ++i)
bits.set(functions[i](string) % size);
}
function test(string)
{
for (var i = 0; i < functions.length; ++i)
if (!bits.test(functions[i](string) % size)) return false;
return true;
}
return {add: add, test: test};
}Пример использования:
var fruits = Bloom(64, [Hash(), Hash()]);
fruits.add('apple');
fruits.add('orange');
alert(fruits.test('cabbage') ? 'Возможно фрукт.' : 'Не фрукт, инфа 100%.');После игр с параметрами, становится понятно, что для них должны быть какие-то оптимальные значения.
Оптимальные значения параметров
Конечно, теоритические оптимальные значения я сам не выводил, просто сходил на Википедию, но и без неё, включив логику, можно прикинуть и уловить некоторые закономерности. Например, нет смысла использовать большой битовый массив, если вы собираетесь хранить там два значения, обратное тоже верно, иначе массив будет перенаселён, что приведёт к росту ошибочных ответов «возможно». Оптимальный размер массива в битах:
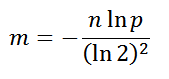
, где
n — предполагаемое количество элементов хранящихся в фильтре-множестве, p — желаемая вероятность ложного срабатывания.Количество хеш-функций должно быть не большим, но и не маленьким. Оптимальное количество:
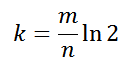
Применим полученные знания:
function OptimalBloom(max_members, error_probability)
{
var size = -(max_members * Math.log(error_probability)) / (Math.LN2 * Math.LN2);
var count = (size / max_members) * Math.LN2;
size = Math.round(size);
count = Math.round(count);
var functions = [];
for (var i = 0; i < count; ++i) functions[i] = Hash();
return Bloom(size, functions);
}Где использовать?
Например, Гуголь использует фильтры Блума в своей BigTable для уменьшения обращений к диску. Оно и не удивительно, ведь по сути, BigTable — это большая очень разреженная многомерная таблица, поэтому большая часть ключей указывает в пустоту. К тому же, данные распиливаются на относительно небольшие блоки-файлы, каждый из которых опрашивается при запросах, хотя может не содержать требуемых данных.
В данном случае, выгодно потратить немного оперативной памяти и сильно уменьшить использование диска. Скажем, чтобы уменьшить нагрузку в 10 раз, необходимо хранить примерно 5 бит информации на каждый ключ. Чтобы уменьшить в 100 раз, нужно порядка 10 бит на ключ. Выводы делайте сами.
Разные мысли
Судя по тестам, оптимальные значения параметров для практики несколько завышены, можно смело понижать порог ложного срабатывания на порядок-два. Только обязательно протестируйте, если будете использовать — возможно, в моих тестах подобралась какая-то уникальная комбинация данных и хеш-функций или я банально где-то ошибся.
Очевидно, что удалять элементы из фильтра невозможно, но это просто решается — достаточно заменить битовый массив на массив счётчиков — инкрементировать при добавлении, декрементировать при удалении. Расход памяти, естественно, возрастает.
Так же очевидно, что невозможно динамически изменять параметры фильтра. Проблема элегантно решается введением иерархии фильтров, каждый последующий более точен, при необходимости иерархия растёт вглубь.
Пожалуй, на этом всё. Пока.