Категорически приветствую! В прошлый раз я писал о вероятностном алгоритме определения принадлежности элемента множеству, в этот раз будет про вероятностную оценку похожести. Не надо большого ума, чтобы додуматься до следующего показателя схожести двух множеств А и Б:
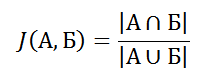
То есть, количество элементов в пересечении делённое на количество элементов в объединении. Эта оценка называется коэффициентом Жаккара (Jaccard, поэтому «J»), коэффициент равен нулю, когда множества не имеют общих элементов, и единице, когда множества равны, в остальных случаях значение где-то посередине.
Давайте прикинем, как посчитать этот коэффициент для пары строковых множеств, скажем, мы задумали выяснить насколько один фрагмент текста похож на другой. Для начала, нам необходимо разбить текст на отдельные слова — это будут элементы наших множеств, затем надо как-то посчитать размеры пересечения и объединения.
Обычно, для эффективного выполнения двух последних операций, множества представляют как хэш-таблицы без ассоциированных с ключами значений, работает такая структура очень быстро. Построение таблицы — O(n), их нужно две, вычисление пересечения — O(n) и вычисление объединения тоже O(n), где n — количество слов в тексте. Вроде всё отлично, но давайте усложним задачу.
Предположим, что у нас есть набор текстовых данных (посты, комментарии, т.д.), хранящийся в базе данных, и при добавлении новых записей, нам необходимо отсеивать слишком похожие на уже существующие. В этом случае, придётся загружать все документы и строить для них хэш-таблицы. Хотя делается это довольно быстро, количество операций напрямую зависит от размеров документов и их количества.
Последняя проблема может быть решена индексированием, скажем, тем же Сфинксом, тогда для сравнения можно загружать только документы, имеющие некоторое подмножество общих слов. Работает это хорошо, но только для маленьких документов, для больших, тестируемые подмножества становятся слишком большими. Решением первой и этой производной проблемы мы с вами и займёмся.
Предположим, у нас есть: два множества А, Б и хэш-функция h, которая умеет считать хэши для элементов этих множеств. Далее, определим функцию hmin(S), которая вычисляет функцию h для всех членов какого-либо множества S и возвращает наименьшее её значение. Теперь, начнём вычислять hmin(А) и hmin(Б) для различных пар множеств, вопрос: чему равна вероятность того, что hmin(А) = hmin(Б)?
Если задуматься, эта вероятность должна быть пропорциональна размеру пересечения множеств — при отсутствии общих членов, она стремится к нулю, и к единице, когда множества равны, в промежуточных случаях она где-то посередине. Ничего не напоминает? Ага, всё верно, это и есть J(А, Б) — коэффициент Жаккара!
Беда в том, что если мы просто посчитаем hmin(А) и hmin(Б) для наших двух фрагментов текста, а затем сравним значения, это нам ничего не даст, т.к. варианта всего два — равно или не равно. Нам надо каким-то образом добыть достаточный объём статистики по нашим множествам, чтобы вычислить близкий к истине J(А, Б). Делается это просто, вместо одной функции h, вводим несколько независимых хэш-функций, а точнее k функций:
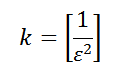
, где ε — желаемая наибольшая величина ошибки. Так, для вычисления J(А, Б) с ошибкой не более чем 0.1, необходимо 100 хэш-функций — не мало. В чём же плюсы?
Во-первых, можно посчитать, так называемую, сигнатуру Hmin(S), т.е. минимумы всех хэш-функций для множества S. Трудоёмкость её вычисления больше, чем при построении хэш-таблицы, но, тем не менее, она линейна, и сделать это для каждого документа нужно всего один раз, например при добавлении в базу, потом достаточно оперировать только сигнатурами.
Во-вторых, как вы могли заметить, сигнатура имеет фиксированный размер при заданной максимальной величине ошибки. Для того чтобы сравнить любые два множества любого размера, необходимо выполнить фиксированное количество операций. Кроме того, в теории, сигнатуры гораздо удобней индексировать. «В теории» потому, что их индексирование не очень хорошо ложится на реляционные базы данных, на полнотекстовые движки тоже не особо. По крайней мере, я не смог придумать, как сделать это красиво.
Как обычно, нам необходимо семейство хэш-функций:
Сам MinHash:
Пример использования:
В реальности, точность будет немного ниже, так как реальные хэш-функции не идеальны. Можно с этим смириться или ввести пару-другую дополнительных функций, хотя пара-другая не сильно поможет.
Почему-то нигде не упоминается, каким же должно быть количество битов выдаваемых функциями. По идее, это количество должно быть таким, чтобы представить все возможные варианты входных значений. Например, в английском языке порядка 250 000 слов, следовательно, достаточно порядка 18 бит. Но лучше, опять же, подстраховаться и добавить пару лишних битов.
Индексировать сигнатуры выгодно не по всем составляющим их значениям, а по небольшому подмножеству. Это уменьшает размер индексов и ускоряет выборку, но таит в себе опасность — может попасться хэш-функция, которая будет иметь минимум на каком-то часто употребляемом слове (предлоги, артикли, т.д.), соответственно селективность индекса будет не самой лучшей. К тому же, это увеличивает вероятность ошибки. Всё-таки это плохая идея.
Посравнивать тексты можно тут. Спасибо за внимание, до новых встреч.
P.S. ХабраСторадж у всех выдаёт ошибку при загрузке картинок или только у меня?
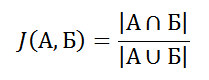
То есть, количество элементов в пересечении делённое на количество элементов в объединении. Эта оценка называется коэффициентом Жаккара (Jaccard, поэтому «J»), коэффициент равен нулю, когда множества не имеют общих элементов, и единице, когда множества равны, в остальных случаях значение где-то посередине.
Как его посчитать?
Давайте прикинем, как посчитать этот коэффициент для пары строковых множеств, скажем, мы задумали выяснить насколько один фрагмент текста похож на другой. Для начала, нам необходимо разбить текст на отдельные слова — это будут элементы наших множеств, затем надо как-то посчитать размеры пересечения и объединения.
Обычно, для эффективного выполнения двух последних операций, множества представляют как хэш-таблицы без ассоциированных с ключами значений, работает такая структура очень быстро. Построение таблицы — O(n), их нужно две, вычисление пересечения — O(n) и вычисление объединения тоже O(n), где n — количество слов в тексте. Вроде всё отлично, но давайте усложним задачу.
Предположим, что у нас есть набор текстовых данных (посты, комментарии, т.д.), хранящийся в базе данных, и при добавлении новых записей, нам необходимо отсеивать слишком похожие на уже существующие. В этом случае, придётся загружать все документы и строить для них хэш-таблицы. Хотя делается это довольно быстро, количество операций напрямую зависит от размеров документов и их количества.
Последняя проблема может быть решена индексированием, скажем, тем же Сфинксом, тогда для сравнения можно загружать только документы, имеющие некоторое подмножество общих слов. Работает это хорошо, но только для маленьких документов, для больших, тестируемые подмножества становятся слишком большими. Решением первой и этой производной проблемы мы с вами и займёмся.
Ключевая идея MinHash
Предположим, у нас есть: два множества А, Б и хэш-функция h, которая умеет считать хэши для элементов этих множеств. Далее, определим функцию hmin(S), которая вычисляет функцию h для всех членов какого-либо множества S и возвращает наименьшее её значение. Теперь, начнём вычислять hmin(А) и hmin(Б) для различных пар множеств, вопрос: чему равна вероятность того, что hmin(А) = hmin(Б)?
Если задуматься, эта вероятность должна быть пропорциональна размеру пересечения множеств — при отсутствии общих членов, она стремится к нулю, и к единице, когда множества равны, в промежуточных случаях она где-то посередине. Ничего не напоминает? Ага, всё верно, это и есть J(А, Б) — коэффициент Жаккара!
Беда в том, что если мы просто посчитаем hmin(А) и hmin(Б) для наших двух фрагментов текста, а затем сравним значения, это нам ничего не даст, т.к. варианта всего два — равно или не равно. Нам надо каким-то образом добыть достаточный объём статистики по нашим множествам, чтобы вычислить близкий к истине J(А, Б). Делается это просто, вместо одной функции h, вводим несколько независимых хэш-функций, а точнее k функций:

, где ε — желаемая наибольшая величина ошибки. Так, для вычисления J(А, Б) с ошибкой не более чем 0.1, необходимо 100 хэш-функций — не мало. В чём же плюсы?
Во-первых, можно посчитать, так называемую, сигнатуру Hmin(S), т.е. минимумы всех хэш-функций для множества S. Трудоёмкость её вычисления больше, чем при построении хэш-таблицы, но, тем не менее, она линейна, и сделать это для каждого документа нужно всего один раз, например при добавлении в базу, потом достаточно оперировать только сигнатурами.
Во-вторых, как вы могли заметить, сигнатура имеет фиксированный размер при заданной максимальной величине ошибки. Для того чтобы сравнить любые два множества любого размера, необходимо выполнить фиксированное количество операций. Кроме того, в теории, сигнатуры гораздо удобней индексировать. «В теории» потому, что их индексирование не очень хорошо ложится на реляционные базы данных, на полнотекстовые движки тоже не особо. По крайней мере, я не смог придумать, как сделать это красиво.
Игрушечная реализация
Как обычно, нам необходимо семейство хэш-функций:
function Hash(size)
{
var seed = Math.floor(Math.random() * size) + 32;
return function (string)
{
var result = 1;
for (var i = 0; i < string.length; ++i)
result = (seed * result + string.charCodeAt(i)) & 0xFFFFFFFF;
return result;
};
}Сам MinHash:
function MinHash(max_error)
{
var function_count = Math.round(1 / (max_error * max_error));
var functions = [];
for (var i = 0; i < function_count; ++i)
functions[i] = Hash(function_count);
function find_min(set, function_)
{
var min = 0xFFFFFFFF;
for (var i = 0; i < set.length; ++i)
{
var hash = function_(set[i]);
if (hash < min) min = hash;
}
return min;
}
function signature(set)
{
var result = [];
for (var i = 0; i < function_count; ++i)
result[i] = find_min(set, functions[i]);
return result;
}
function similarity(sig_a, sig_b)
{
var equal_count = 0;
for (var i = 0; i < function_count; ++i)
if (sig_a[i] == sig_b[i]) ++equal_count;
return equal_count / function_count;
}
return {signature: signature, similarity: similarity};
}Пример использования:
var set_a = ['apple', 'orange'];
var set_b = ['apple', 'peach'];
var min_hash = MinHash(0.05);
var sig_a = min_hash.signature(set_a);
var sig_b = min_hash.signature(set_b);
alert(min_hash.similarity(sig_a, sig_b));Тонкие моменты
В реальности, точность будет немного ниже, так как реальные хэш-функции не идеальны. Можно с этим смириться или ввести пару-другую дополнительных функций, хотя пара-другая не сильно поможет.
Почему-то нигде не упоминается, каким же должно быть количество битов выдаваемых функциями. По идее, это количество должно быть таким, чтобы представить все возможные варианты входных значений. Например, в английском языке порядка 250 000 слов, следовательно, достаточно порядка 18 бит. Но лучше, опять же, подстраховаться и добавить пару лишних битов.
Посравнивать тексты можно тут. Спасибо за внимание, до новых встреч.
P.S. ХабраСторадж у всех выдаёт ошибку при загрузке картинок или только у меня?