Аннотация
 Эта статья написана в продолжении первой части статьи про работу с бинарными изображениями, в которой рассказывается как подсчитывать объекты. Однако от одного подсчета толку мало, часто хочется узнать некоторые геометрические параметры распознаваемых объектов. Кажется, что тут считать — узнал количество восьмерок — площадь равна 19, посчитал количество семерок — площадь равна 7 (см. картинку в Аннотации).
Эта статья написана в продолжении первой части статьи про работу с бинарными изображениями, в которой рассказывается как подсчитывать объекты. Однако от одного подсчета толку мало, часто хочется узнать некоторые геометрические параметры распознаваемых объектов. Кажется, что тут считать — узнал количество восьмерок — площадь равна 19, посчитал количество семерок — площадь равна 7 (см. картинку в Аннотации). Делая так, мы будем вынуждены использовать дополнительный проход по изображению, желательно этого избегать — в пользу повышения эффективности реализации. Как и было запланировано, в этом топике рассказывается о подсчете геометрических характеристик объектов без дополнительного прохода.
А так же: фактор формы и розы Гвидо-Гранди и чем отличается квадрат от прямоугольника, а он от звезды.
Предыдущие части статьи:
Часть 1
Подсчет объектов и вычисление геометрических признаков
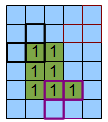 В самом начале разберемся с площадью. В предыдущей статье рассматривалось 5 позиций ABC-маски, пятая позиция включала в себя объединение двух размеченных связных областей, которые оказались под разными, но эквивалентными номерами.
В самом начале разберемся с площадью. В предыдущей статье рассматривалось 5 позиций ABC-маски, пятая позиция включала в себя объединение двух размеченных связных областей, которые оказались под разными, но эквивалентными номерами. Добавим в исходный код — в каждую из условных позиций следующую логику:
- Для позиций с 1-ой по 5-ую: в них следует увеличить площадь объекта с текущей меткой на единицу.
- Для 5-ой позиции дополнительно, при объединении областей под эквивалентными номерами B и C выполняем S(B) = S(B) + S©.
Для краткости, приведу код исходного скрипта только с новыми строками в каждой из позиций.
if A == 0 then
elseif B == 0 & C == 0 then
/.../
Squares(cur) = Squares(cur) + 1;
elseif B ~=0 & C == 0 then
/.../
Squares(B) = Squares(B) + 1;
elseif B == 0 & C ~= 0 then
/.../
Squares© = Squares© + 1;
elseif B ~= 0 & C ~= 0 then
Squares(B) = Squares(B) + 1;
if B == C then
Im(i,j) = B;
else
/.../
Squares(B) = Squares(B) + Squares©;
Squares© = 0;
end
/.../
end
* This source code was highlighted with Source Code Highlighter.
Листинг 1 — Изменения в коде скрипта для подсчета площади размечаемых объектов.
С подсчетом периметра объекта чуть сложнее. Как и в ситуации площадью если B == 0 или C == 0
мы так же должны увеличить периметр. Однако этого будет недостаточно. Введем в рассмотрение еще одну ABC-маску — такой же уголок (черная маска на рисунке), но перевернутый на 180 градусов (пурпурная маска на рисунке). Это добавит нам еще три возможных ситуации, но рассматривать их следует только в рамках позиции номер 5.
elseif B ~= 0 & C ~= 0 then
Squares(B) = Squares(B) + 1;
if B == C then
Im(i,j) = B;
else
Im(i,j) = B;
Im(Im == C) = B;
Squares(B) = Squares(B) + Squares©;
Squares© = 0;
Perimetrs(B) = Perimetrs(B) + Perimetrs©;
Perimetrs© = 0;
end
A = Im(i,j);
kn = j + 1;
if kn > n then
kn = n;
B = 0;
else
B = Im(i,kn);
end
km = i + 1;
if km > m then
km = m;
C = 0;
else
C = Im(km,j);
end
if B == 0 & C == 0 then
Perimetrs(A) = Perimetrs(A) + 1;
elseif B ~= 0 & C == 0 then
Perimetrs(A) = Perimetrs(A) + 1;
elseif B == 0 & C ~= 0 then
Perimetrs(A) = Perimetrs(A) + 1;
end
end
* This source code was highlighted with Source Code Highlighter.
Листинг 2 — Изменения в коде скрипта для подсчета периметра объекта.
Обобщая этот принцип, можно утверждать, что с использованием ABC маски и алгоритма разметки объектов можно подсчитать любые геометрические признаки, которые обладают свойством линейности при слиянии областей, то есть пусть объект 3 состоит из двух частей: Obj3 = Obj1 + Obj2, тогда его признак F(Obj3) = F(Obj1) + F(Obj2). Примером подобного может стать центр тяжести объекта.
Фактор формы
Со школьной скамьи всем известно, что для любой геометрической фигуры можно рассчитать площадь и периметр. Например, для окружности формулы выглядят так

Рассмотрим интересное соотношение соотношение (3), которое связывает в себе и площадь и периметр — это и есть один из видов факторов формы. Подставляя в него соответствующие формулы для площади и периметра окружности, легко понять, что для окружностей любых радиусов фактор формы равен 0.
Однако для окружности все достаточно просто, а что будет с более сложными фигурами? В статье мы рассмотрим так называемые розы Гвидо-Гранди (Рисунок 1).

Рисунок 1 — Множество роз Гвидо-Гранди.
Для простоты реализации, что бы не связываться с полярной системой координат, я переделал исходные формулы для декартовых координат (4), однако они не эквивалентны исходным правилам построения, но результат получается похожий и пригодный для наших целей (Рисунок 1).

Как же ведет себя фактор формы (3) в зависимости от изменяемого параметра розы? Это продемонстрировано на графике на рисунке 2.
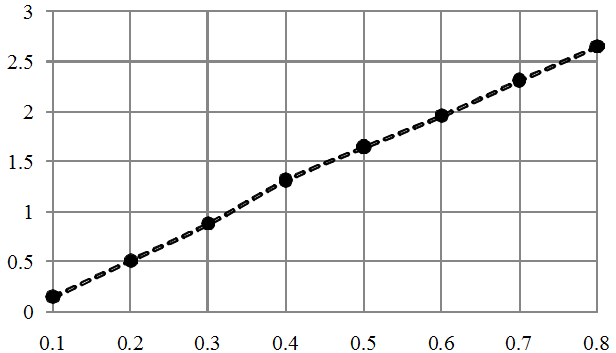
Рисунок 2 — Фактор формы (3) розы Гвидо-Гранди по горизонтальной оси в зависимости от изменяемого параметра по вертикальной оси.
Становится очевидной линейная зависимость, уверен, что она имеет аналитическую запись и формулу для этого можно вывести достаточно легко. но пусть это будет маленькая головоломка для читателей.
В итоге, используя простое соотношение между площадью и периметром мы получили признак, по которому можно идентифицировать фигуру — распознать. На практике, этот признак лишь один из многих в векторе признаков. Так как он хотя и обладает устойчивость к искажениям гомотетии (подобия, масштаба), но из за ошибок в контуре фигуры, порождаемых бинаризацией и квантованием, вычисляется с точностью +(-)0.15, при варьировании радиуса розы.
Теперь посмотрим, как с помощью данного признака отличать квадраты и прямоугольники. Для краткости, приводится только иллюстрация — рисунок 3.
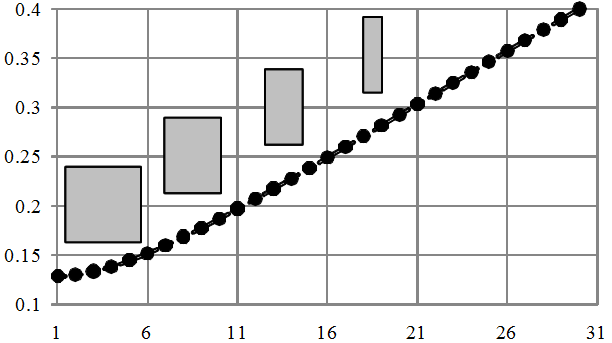
Рисунок 3 — Изменение фактора формы при вытягивании квадрата в прямоугольник.
Здесь зависимость уже нелинейная, это очевидно и из аналитической формулы.
Существует множество подобных эвристических факторов форм, к которым можно отнести и компактность фигуры.
Заключение
Вот здесь можно скачать скрипт SciLab для своих экспериментов, который включает:
- Построение контура звезд.
- Заливка с использованием алгоритма из этой статьи.
- Разметка и подсчет площади и периметра.
- Расчет фактора формы.
Архив зашифрован с паролем, который указан в первом комментарии, прошу прощения за такие неудобства, но это с целью защиты от копипастеров, которые комментарии, как правило, не копируют.
Спасибо всем прочитавшим, жду ваших комментариев. Если кто-то знаком с литературой где описываются факторы форм — прошу дать ссылки, не смог ничего найти до публикации, чтобы иметь самокритику.
UPD: 06.06.11, 15:28