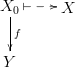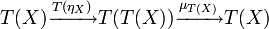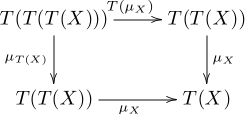Введение
Кажется, монады в программировании стали загадкой века. И для этого есть две причины:- недостаточное знание теории категорий;
- многие авторы стараюстся не упоминать категории вообще.
Мы начнём с простого введения в категории и функторы, затем дадим определение монады, приведём простые примеры монад в категориях и в конце приведём монадическую терминологию используемую в языках программирования.
Я уверен, что монады с точки зрения категорий почти элементарны.
Содержание
- Категория
- Функтор
- Естественное преобразование
- Монада
- Монады исключения и состояния
- Монады в программировании
- Ссылки
Категория
Категория состоит из объектов и морфизмов между ними. Термин «морфизм» не совсем корректен (он не обязан превращать что-то), по этому, часто, морфизм называют «стрелкой» для того, чтобы показать его абстрактную сущность.Мы будем использовать термин «стрелка» во всех случаях, кроме того, когда стрелка обозначает некоторую функцию, тогда мы будем называть её «морфизм», но для меня он всё равно останется стрелкой.
Неважно, чем является объект или стрелка, важно только выполнение следующих свойств:
Стрелка рисуется между объектами (при этом объект может быть одним тем же); это обозначается следующим образом: f: a → b, где f это стрелка, а a и b — объекты.
- Для стрелок f: a → b и g: b → c существует такая стрелка h: a → c называемая композицией: h = g ° f.

- Для каждого объекта a существует единичная стрелка, ida: a → a, такая, что для любого f: a → b следующее верно:
f ° ida = f и для любого g: c → a мы имеем ida ° g = g. - Композиция ассоциативна: f ° (g ° h) = (f ° g) ° h.
Замечание. В виду чрезвычайно абстрактной природы этой записи, мы не можем ожидать, что «все объекты» или «все стрелки из a к b» образуют множество. Категории, где они являются множествами называются «малые» или «локально малые».
Примеры категорий
Примеры «классических» категорий:- Set — категория всех множеств. Её объекты это все множества, а морфизмы — функции над множествами.
- Setf — категория всех конечных множеств и функций между ними.
- Rel — категория, где объекты это все множества, а бинарные отношения играют роль морфизмов. Композиция объедена через внутеннее объединение.
- Part — категория всех множеств и частичных функций как морфизмов. Частичная функция из X к Y это функция из подмножества Xo ⊂ X к Y:
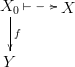
- Top — категория всех топологических пространств и непрерывных функций между ними.
- Любая группа может быть рассмотрена как категория: группа элементов это морфизмы над единственным объектом.
Тождественная функция это нейтральный элемент группы. А композицией является умножение. - Частично упорядоченное множество может быть представленно как категория. Элементы множества это объекты. Добавим одну стрелку a → b для каждой пары a, b так, что a < b и единичную стрелку a → a для каждого a.
Для каждой пары объектов существует не более, чем одна стрелка и, так как частичный порядок транзитивен, мы имеем композицию (a < b, b < c => a < c), то есть можно не переживать о его ассоциативности. - Как особый случай прошлого примера — множество целых чисел [N… M] можно считать категорией.
- Любой ориентированный граф может быть преобразован в категорию, если считать его пути стрелками. Пустой путь является единичным морфизмом, а конкатенация путей будет композицией.
- Натуральные числа как объекты, матрицы как стрелки. Любая матрица NxM будет стрелкой N → M. Перемножение матриц будет играть роль композиции, а единичная матрица NxN будет единичной стрелкой N → N.
Дополнительный материал
Просто определить изоморфизм в категории — им является тот, что имеет инверсию. То есть, в том случае, если мы имеем f: a → b и g: b → a, и выполняется f ° g = idb и g ° f = id a. Это определение потребуется нам позже. Также возможно определить мономорфизм и эпиморфизм, это несколько сложнее и выходит за рамки данной статьи.Помните объекты [0… N] из прошлой главы? Существуют особые категории: 1 = [0] и 2 = [0… 1]. Первая является одним объектом с единственным морфизмом, вторая — двумя объектами и тремя морфизмами.
Образуют ли сами категории категорию? Да, но тогда нам следует дать определение стрелок между ними. Они являются стрелками второго порядка и называются функторами.
Функтор
Функтор отображает одну категорию в другую. Для того, чтобы сделать это, нам нужно отобразить объекты из первой категории во вторую и стрелки (морфизмы) из первой категории в стрелки второй категории непротиворечивым образом.Какую непротиворечивость мы ожидаем? Пусть X и Y будут двумя категориями; определим функтор F: X → Y. Теперь нам нужно отобразить объекты из X в Y, имея для каждого a в X объект F(a) в Y и для каждой стрелки f в X мы должны иметь стрелку F(f) в Y.
Для непротиворечивости должны выполняться следующие правила:
- для f: a → b имеем F(f): F(a) → F(b) — сохраняются домен и кодомен;
- для ida: a → a имеем F(ida) = idF(a): F(a) → F(a) — сохраняется единица;
- для f: a → b и g: b → c F(g ° f) = F(g) ° F(f) — сохраняется композиция.
Примеры функторов
- Тождественный функтор для категории X. Хотя тождественность X → X сохраняет объекты и стрелки неизмененными это всё еще функтор.
- Setf Set — функтор, который включает Setf в Set, отображая конечные множества в самих себя, то же самое с функциями. Обратите внимание, что это не тождественный функтор.
- Set → Top аналогично предыдущему примеру, этот функтор делает Set частью Top. Каждое множество отображается в дискретное топологическое пространство.
- Для любого множества A мы можем определить следующий функтор:
(- xA): Set → Set — он отобразит любое множество X в декартово произведение X × A.
- Для любого множества A можно определить функтор PA: Set → Set, который отобразит любое множество X в XA — множество функций из A в X.
- Set Part вводит множеста в множества с частичными функциями — отображает множества и функции в них самих.
- Обратным к п.6 является функтор +Null: Part → Set — этот функтор добавляет «расширение» Null к каждому множеству X ↦ (X + Null) так, что частичная функция X → Y отображается в функцию (X + Null) → (Y + Null).
Упражнение. Определите такое же расширение для частичных функций.
Посмотрим на малые категории и их функторы.
- Если мы примем группы за категории, то чем же будут их функторы? Функтор должен сохранять единичный морфизм и композицию. Следовательно, функтор это гомоморфизм группы.
- Любая функция сохраняющая порядок (т.н. монотонная) между двумя частично упорядоченным множествами является функтором.
- Возьмем пару ориентированных графов и отображение, которое сохраняет ребра. Мы можем расширить это отображение до функции, что отображает путь из одного графа в пути на другом графе. Эта функция, по определению, сохраняет связи и пустые пути, таким образом это функтор из одной созданной по графу категории в другую.
- Помните категорию 1? И так, как будет выглядеть функтор из 1 в категорию C? 1 имеет всего лишь один объект и тождественный морфизм. Таким образом определение этого функтора равносильно выбору объекта из C и наоборот — для любого объекта X в категории C мы можем определить функтор PointX: 1 → C.
Естественное преобразование
Должно быть, это самая сложная часть. Предположим, что мы имеем два функтора F, G: X → Y. Естественное преобразование η: F → G определено, когда для каждого объекта x ∈ X существует стрелка η(x): F(x) → G(x) в Y и мы имеем следующее свойство:- для всех f: a → b верно равенство: G(f) ° η(a) = η(b) ° F(f).
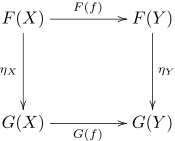
По этому оно называется «естественным» — оно действует непротиворечиво с действиями функторов на стрелки.
Примеры естественных преобразований
- Помните функтор точки? И так, если в категории C мы имеем стрелку f: a → b, эта стрелка определяет естественное преобразование из Pointa в Pointb. Это отношение один-к-одному между преобразованием функтора точки и стрелками категории.
- Возьмем два множества A и B и функцию f: A → B. Эта функция определяет естественное преобразование между функторами (- xA),(- xB): Set → Set. (- xf): (- xA) → (- xB) по следующей формуле: (x, a) ↦ (x, f(a)).
Можно записать это определение в следующем виде:
Так как для каждого множества A существует функция A → (.), где (.) синглетон, мы имеем естественное преобразование (- xA) → 1, что является для каждого объекта X проекцией: X ⨯ A → X.(define (cartesian f) (lambda (x a) (list x (f a))))
Опять же, это определение можно записать следующим образом:
(define (return x) (lambda (a) (x)))
Монада
Монада в категории C это эндофунктор T: C → C с двумя естественными преобразованиями: η: 1 → T и μ: T ° T → T.Обозначим за T(η): T → T ° T преобразование, результатом которого является применение T к η и T(μ): (T ° T) ° T → T ° T.Пользуясь этими определениями запишем две аксиомы монад:
- T(η) ° μ это тождество T → T
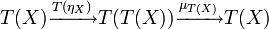
- T(μ) ° μ равносильно μ ° μ:

Примеры монад
- Для любой категории C может быть определена тождественная монада, состоящая из тождественного функтора и тождественного морфизма.
- Предположим, что у нас есть группа G. Определим монаду MG в Set. Функтор монады будет следующим:
X ↦ X × G.
u(X): X → X × G отображает элемент x в пару (x, e), где e это единица группы.
MG(MG(X)) = (idX, mG), где mG это умножение групп. - Списки в Set. Результатом применения функтора, назовем его List, для множества X является множество всех списков (x1, x2, x3...) элементов из X, включая пустое. Этот функтор станет популярной монадой, если мы добавим u и m. Пусть uX: X → List(X) создает список из единственного элемента для каждого x ∊ X и mX: List(List(X)) → List(X) отображает список списков в плоский список.
Операция замыкания. Не уверен, много ли она имеет общего с той же операцией из «computer science».
Помните, что мы можем считать частично-упорядоченные множества и их функции, сохраняющие порядок, как категории и функторы?
Монотонная (сохраняющая порядок) функция C: X → X называется замыканием, если ∀ x ∊ X x <= C(x) и C(C(x)) = C(x).
Эти два условия являются ни чем иным, как аксиомами монад, применёнными к частично-упорядоченным множествам, считая, что монады в частично-упорядоченных множествах и есть замыкания. Также можно попытаться применить это к частично-упорядоченным множествам путей графа.
Монады исключения и состояния
Монада исключения
Мы в категории Part. Возьмём множество A и определим следующий функтор:PlusNull: X ↦ (X+Null)
Мы уже рассматривали этот функтор, в прошлый раз он был из Part в Set. На этот раз мы создадим его с включением Set в Part, то есть получим эндофунктор.
Почему он является монадой? Нам потребуется ещё uX: X → (X+Null) и mX: ((X+Null)+Null) → (X+Null).
В первом случае это простое включение, а во втором мы отображаем оба Null синглтона в Null. На Lisp это выглядит следующим образом:
(define (ux x) x)
(define (mx x) x)
Монада состояния
Мы в категории Set. Возьмём множество A и определим следующий функтор:X ↦ (X × A)A
Об A можно думать, как о множестве состояний некоторого автомата, тогда (X × A)A включает в себя все состояния автомата на X с выводом в X, то есть всех функций A → (A × X), первый компонент является преобразованием, а второй выводом в X.
Почему это монада? uX: X → (A × X)A отображает любой элемент x ∊ X в функцию, являющуюся тождественной на A и константой x на X.
Опишем это на Lisp:
(define (ux x)
(lambda (a) (list a x)))
А что на счёт mX: (A × (A × X)A)A → (A × X)A?
Имея коллекцию автоматов mX: (A × (A × X)A)A, которая имеет A как множество состояний, которое выводится в другую коллекцию автоматов (эти тоже имеют A как множество состояний, но X как множество выводов). Каким образом, для такого составного автомата, можно найти соответствие в множестве A?
Опишем это на Lisp:
(define (mx f)
(let (tr1 out1)
((car f) (cadr f))) ;два компонента f: A → (A × (A × X))^A
(lambda (a)
(let a1 (tr1 a)) ;состояния после первого преобразования
(let f2 (out1 a)) ;отображение состояния в другой автомат
(let (tr2 out2) ((car f2) (cadr f2))) ;составные части второго автомата
(list (tr2 a1) (out2 a1))))
Скучное упражнение. Докажите, что это действительно монада.
Монады в программировании
С точки зрения категорий, функциональное программирование состоит из представления программ как морфизмов в категории f: X → Y, где X это «ввод», а Y это «вывод».Преимущество такой модели состоит в том, что мы можем погрузить все наши высказывания относительно программ в очень стабильную теорию категорий; возможно менять сущность объектов и категорий, изменять логику лежащего в основе топоса и быть на 100% уверенными в том, о чем мы говорим. Например, вместо «нечёткой логики» можно использовать интуиционистскую логику или семнтику Крипке.
Кажется, что некоторые техники программирования не подходят для такой модели, например исключения или побочные эффекты.
Одно из решений проблемы исключений это введение NullObject или числового значения NaN.
Например, если наша функция не определена на всей области X, мы можем расширить её используя значения из (Y+Null), также как и в монаде исключения.
А для функций имеющих состояние подойдёт, соответственно, монада состояния.
Монада IO в Haskell
В Haskell ввели монаду IO, чтобы избежать сложности с описанием того, каким образом функции могут иметь побочные эффекты.Они использовали следующий трюк. Возьмите монаду состояния, как мы делали до этого. Вообразите, что A это множество состояний, представляющее внешний мир, а X это множество результатов функции.
В этой модели каждое состояние автомата становится функцией. Далее A представляется как декартово произведение двух множеств String, где первый компонент это «ввод», а второй «вывод».
Для этого введение специальные функции преобразования, первая, getc, забирает символ из ввода, а другая, putc, добавляет символ к выводу.
Интересно, чего же конкретно они пытались этим добиться.
Ссылки и примечания
- Википедия как основной источник ссылок.
- Эта статья как сложное, скучное, но исчерпывающее объяснения монадической терминологии используемой в программировании.
- “Comprehending Monads” от Frederik Eaton — трехстраничный словарик терминов и обозначений.
- В Haskell u называют return, а m называют комбинатором или join
- Многие книги по Haskell упоминают List как пример монады имея в то же время особую реализацию монады состояния.
- Еще один пример монады это map/reduce от Google.