Вступление.
Прежде всего стоит сказать, что такое Код Хэмминга и для чего он, собственно, нужен. На Википедии даётся следующее определение:
Коды Хэмминга — наиболее известные и, вероятно, первые из самоконтролирующихся и самокорректирующихся кодов. Построены они применительно к двоичной системе счисления.
Другими словами, это алгоритм, который позволяет закодировать какое-либо информационное сообщение определённым образом и после передачи (например по сети) определить появилась ли какая-то ошибка в этом сообщении (к примеру из-за помех) и, при возможности, восстановить это сообщение. Сегодня, я опишу самый простой алгоритм Хемминга, который может исправлять лишь одну ошибку.
Также стоит отметить, что существуют более совершенные модификации данного алгоритма, которые позволяют обнаруживать (и если возможно исправлять) большее количество ошибок.
Сразу стоит сказать, что Код Хэмминга состоит из двух частей. Первая часть кодирует исходное сообщение, вставляя в него в определённых местах контрольные биты (вычисленные особым образом). Вторая часть получает входящее сообщение и заново вычисляет контрольные биты (по тому же алгоритму, что и первая часть). Если все вновь вычисленные контрольные биты совпадают с полученными, то сообщение получено без ошибок. В противном случае, выводится сообщение об ошибке и при возможности ошибка исправляется.
Как это работает.
Для того, чтобы понять работу данного алгоритма, рассмотрим пример.
Подготовка
Допустим, у нас есть сообщение «habr», которое необходимо передать без ошибок. Для этого сначала нужно наше сообщение закодировать при помощи Кода Хэмминга. Нам необходимо представить его в бинарном виде.
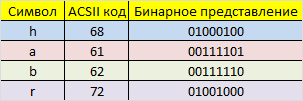
На этом этапе стоит определиться с, так называемой, длиной информационного слова, то есть длиной строки из нулей и единиц, которые мы будем кодировать. Допустим, у нас длина слова будет равна 16. Таким образом, нам необходимо разделить наше исходное сообщение («habr») на блоки по 16 бит, которые мы будем потом кодировать отдельно друг от друга. Так как один символ занимает в памяти 8 бит, то в одно кодируемое слово помещается ровно два ASCII символа. Итак, мы получили две бинарные строки по 16 бит:
 и
и 
После этого процесс кодирования распараллеливается, и две части сообщения («ha» и «br») кодируются независимо друг от друга. Рассмотрим, как это делается на примере первой части.
Прежде всего, необходимо вставить контрольные биты. Они вставляются в строго определённых местах — это позиции с номерами, равными степеням двойки. В нашем случае (при длине информационного слова в 16 бит) это будут позиции 1, 2, 4, 8, 16. Соответственно, у нас получилось 5 контрольных бит (выделены красным цветом):
Было:

Стало:

Таким образом, длина всего сообщения увеличилась на 5 бит. До вычисления самих контрольных бит, мы присвоили им значение «0».
Вычисление контрольных бит.
Теперь необходимо вычислить значение каждого контрольного бита. Значение каждого контрольного бита зависит от значений информационных бит (как неожиданно), но не от всех, а только от тех, которые этот контрольных бит контролирует. Для того, чтобы понять, за какие биты отвечает каждых контрольный бит необходимо понять очень простую закономерность: контрольный бит с номером N контролирует все последующие N бит через каждые N бит, начиная с позиции N. Не очень понятно, но по картинке, думаю, станет яснее:
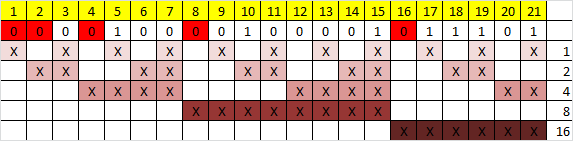
Здесь знаком «X» обозначены те биты, которые контролирует контрольный бит, номер которого справа. То есть, к примеру, бит номер 12 контролируется битами с номерами 4 и 8. Ясно, что чтобы узнать какими битами контролируется бит с номером N надо просто разложить N по степеням двойки.
Но как же вычислить значение каждого контрольного бита? Делается это очень просто: берём каждый контрольный бит и смотрим сколько среди контролируемых им битов единиц, получаем некоторое целое число и, если оно чётное, то ставим ноль, в противном случае ставим единицу. Вот и всё! Можно конечно и наоборот, если число чётное, то ставим единицу, в противном случае, ставим 0. Главное, чтобы в «кодирующей» и «декодирующей» частях алгоритм был одинаков. (Мы будем применять первый вариант).
Высчитав контрольные биты для нашего информационного слова получаем следующее:

и для второй части:

Вот и всё! Первая часть алгоритма завершена.
Декодирование и исправление ошибок.
Теперь, допустим, мы получили закодированное первой частью алгоритма сообщение, но оно пришло к нас с ошибкой. К примеру мы получили такое (11-ый бит передался неправильно):

Вся вторая часть алгоритма заключается в том, что необходимо заново вычислить все контрольные биты (так же как и в первой части) и сравнить их с контрольными битами, которые мы получили. Так, посчитав контрольные биты с неправильным 11-ым битом мы получим такую картину:

Как мы видим, контрольные биты под номерами: 1, 2, 8 не совпадают с такими же контрольными битами, которые мы получили. Теперь просто сложив номера позиций неправильных контрольных бит (1 + 2 + 8 = 11) мы получаем позицию ошибочного бита. Теперь просто инвертировав его и отбросив контрольные биты, мы получим исходное сообщение в первозданном виде! Абсолютно аналогично поступаем со второй частью сообщения.
Заключение.
В данном примере, я взял длину информационного сообщения именно 16 бит, так как мне кажется, что она наиболее оптимальная для рассмотрения примера (не слишком длинная и не слишком короткая), но конечно же длину можно взять любую. Только стоит учитывать, что в данной простой версии алгоритма на одно информационное слово можно исправить только одну ошибку.
Примечание.
На написание этого топика меня подвигло то, что в поиске я не нашёл на Хабре статей на эту тему (чему я был крайне удивлён). Поэтому я решил отчасти исправить эту ситуацию и максимально подробно показать как этот алгоритм работает. Я намеренно не приводил ни одной формулы, дабы попытаться своими словами донести процесс работы алгоритма на примере.
Источники.
1. Википедия
2. Calculating the Hamming Code