Иногда очень интересно провести имитацию броска кости. Для этого существует эффективный алгоритм, который позволяет сгенерировать значение выпавшее на верхней грани, используя псевдослучайное число 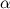 из равномерного распределения на
из равномерного распределения на ![[0,1]](https://habrastorage.org/r/w1560/getpro/geektimes/post_images/1e5/668/a24/1e5668a24690f7b412a044dbc14ad6bd.png) . А именно:
. А именно: 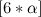 , где
, где  — взятие целой части у аргумента.
— взятие целой части у аргумента.
Но предположим, что у нас «нечестная» кость и грани выпадают неравномерно. Пусть наша кость имеет K граней, и вероятность выпадения грани
вероятность выпадения грани 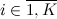 . При этом выполняется естественное ограничение
. При этом выполняется естественное ограничение 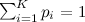 . Постараюсь ответить на вопрос: как смоделировать псевдослучайную последовательность с таким распределением?
. Постараюсь ответить на вопрос: как смоделировать псевдослучайную последовательность с таким распределением?

Рассмотрим «наивный» вариант генерации такого распределения. Введем понятие частичных сумм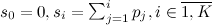 , можно выписать равенство
, можно выписать равенство 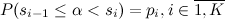 . Осталось по известным
. Осталось по известным 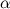 и
и 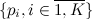 найти конкретное i. Если просто перебирать по всем i начиная с 1 и заканчивая K, то в среднем требуется
найти конкретное i. Если просто перебирать по всем i начиная с 1 и заканчивая K, то в среднем требуется 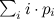 операций сравнения. В худшем случае, который, кстати, встречается с вероятностью
операций сравнения. В худшем случае, который, кстати, встречается с вероятностью 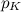 , нам потребуется K сравнений, для примера с графика выше, он возникает с вероятностью 0.45473749. В среднем же требуется 7.5 сравнений и генерация одной случайной величины. Количество операций заставляет грустить особенно, если требуется смоделировать большое количество бросков неправильной костью.
, нам потребуется K сравнений, для примера с графика выше, он возникает с вероятностью 0.45473749. В среднем же требуется 7.5 сравнений и генерация одной случайной величины. Количество операций заставляет грустить особенно, если требуется смоделировать большое количество бросков неправильной костью.
Одна из идей как решить незадачу состоит в том, чтобы подобрать такую правильную кость, посмотрев на которую можно грубо приблизить нашу неправильную кость и сделать это очень быстро. Этот метод называется методом Чена, так же его можно найти под названиями «cutpoint method» или методом «индексного поиска».
Суть метода очень проста, разделим отрезок![[0,1]](http://mathurl.com/a5nwa6n.png) на M равных частей. Введем дополнительный массив r длины M. В элементе
на M равных частей. Введем дополнительный массив r длины M. В элементе 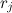 массива будет хранится i, такая что
массива будет хранится i, такая что 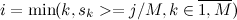 :
:
Алгоритм генерации нового значения в таком случае принимает следующий вид:
В худшем случае для примера, приведенного выше, нам потребуется (при M равном 9) 4 сравнения с вероятностью 0.03712143. В среднем же понадобится генерация одной случайной величины и 1.2 сравнения. Если памяти очень много и этап подготовки данных (задание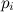 ) относительно редок, M можно выбирать сколь угодно большим.
) относительно редок, M можно выбирать сколь угодно большим.
Метод просто в реализации и дает значительный выигрыш в скорости генерации большого количества реализаций одной и той же случайной величины, особенно в случае большого числа почти одинаковых состояний. На всякий случай приблизительная реализация на c++ выложена на pastebin.
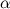 из равномерного распределения на
из равномерного распределения на ![[0,1]](https://habrastorage.org/getpro/geektimes/post_images/1e5/668/a24/1e5668a24690f7b412a044dbc14ad6bd.png) . А именно:
. А именно:  , где
, где  — взятие целой части у аргумента.
— взятие целой части у аргумента.Но предположим, что у нас «нечестная» кость и грани выпадают неравномерно. Пусть наша кость имеет K граней, и
 вероятность выпадения грани
вероятность выпадения грани 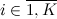 . При этом выполняется естественное ограничение
. При этом выполняется естественное ограничение  . Постараюсь ответить на вопрос: как смоделировать псевдослучайную последовательность с таким распределением?
. Постараюсь ответить на вопрос: как смоделировать псевдослучайную последовательность с таким распределением?#Naive approach
len<-10
ps<-seq(len,2, by=-1)
ps<- 1/ps^2
ps<-ps/sum(ps)
ss<-cumsum(ps)
gen_naiv <- function() {
alpha<-runif(1)
return (min(which(alpha<ss)))
}
#sample
val<-c()
len<-10000
for(i in 1:len) {
val<-append(val, gen_naiv())
}
vals<-factor(val)
plot(vals)
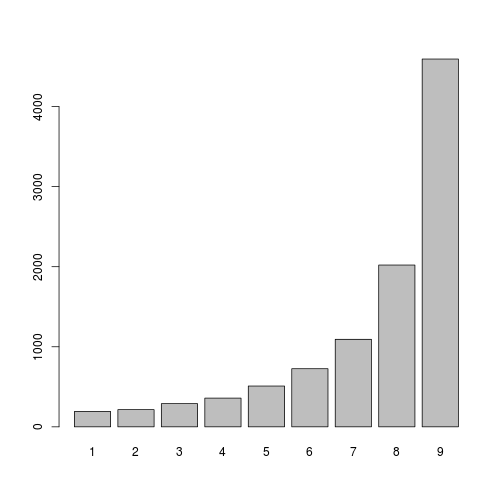
Рассмотрим «наивный» вариант генерации такого распределения. Введем понятие частичных сумм
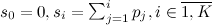 , можно выписать равенство
, можно выписать равенство 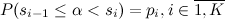 . Осталось по известным
. Осталось по известным 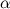 и
и 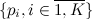 найти конкретное i. Если просто перебирать по всем i начиная с 1 и заканчивая K, то в среднем требуется
найти конкретное i. Если просто перебирать по всем i начиная с 1 и заканчивая K, то в среднем требуется 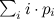 операций сравнения. В худшем случае, который, кстати, встречается с вероятностью
операций сравнения. В худшем случае, который, кстати, встречается с вероятностью 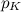 , нам потребуется K сравнений, для примера с графика выше, он возникает с вероятностью 0.45473749. В среднем же требуется 7.5 сравнений и генерация одной случайной величины. Количество операций заставляет грустить особенно, если требуется смоделировать большое количество бросков неправильной костью.
, нам потребуется K сравнений, для примера с графика выше, он возникает с вероятностью 0.45473749. В среднем же требуется 7.5 сравнений и генерация одной случайной величины. Количество операций заставляет грустить особенно, если требуется смоделировать большое количество бросков неправильной костью.Одна из идей как решить незадачу состоит в том, чтобы подобрать такую правильную кость, посмотрев на которую можно грубо приблизить нашу неправильную кость и сделать это очень быстро. Этот метод называется методом Чена, так же его можно найти под названиями «cutpoint method» или методом «индексного поиска».
Суть метода очень проста, разделим отрезок
![[0,1]](http://mathurl.com/a5nwa6n.png) на M равных частей. Введем дополнительный массив r длины M. В элементе
на M равных частей. Введем дополнительный массив r длины M. В элементе 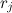 массива будет хранится i, такая что
массива будет хранится i, такая что 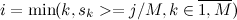 :
:#Preprocessing
ss<-cumsum(ps)
ss<-append(ss, 0, after=0)
M<-length(ss)
rs<-c()
for(k in 0:(M-1)) rs<-append(rs, min(which(ss>=k/M)))
Алгоритм генерации нового значения в таком случае принимает следующий вид:
#chen's method finite discrete distribution generator
gen_dfd <- function() {
M<-10
alpha<-runif(1)
idx<-rs[floor(alpha*M)+1]
return (idx-1+min(which(alpha<ss[idx:(M+1)]))-1)
}
#sample code
val<-c()
len<-10000
for(i in 1:len) {
val<-append(val, gen_dfd())
}
vals<-factor(val)
plot(vals)
В худшем случае для примера, приведенного выше, нам потребуется (при M равном 9) 4 сравнения с вероятностью 0.03712143. В среднем же понадобится генерация одной случайной величины и 1.2 сравнения. Если памяти очень много и этап подготовки данных (задание
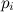 ) относительно редок, M можно выбирать сколь угодно большим.
) относительно редок, M можно выбирать сколь угодно большим.Метод просто в реализации и дает значительный выигрыш в скорости генерации большого количества реализаций одной и той же случайной величины, особенно в случае большого числа почти одинаковых состояний. На всякий случай приблизительная реализация на c++ выложена на pastebin.