Доброго времени суток. Хочу поделиться своими знаниями о работе со статистикой в R.
Многим из нас приходится сталкиваться с различными данными на работе и в повседневной жизни. Качественно и правильно их обработать и проанализировать не так сложно. В этой серии статей я покажу применения некоторых статистических тестов.
Заинтересовались? Добро пожаловать под кат.
Часть 2: Тесты качественных данных
Часть 3: Тесты количественных данных
Заранее хочу извиниться, что часто использую английские термины, а также за возможный их некорректный перевод.
Первая статья посвящена такому интересному тесту, как бинарная классификация. Это тестирование, которое состоит в проверке объектов на наличие какого-то качества. Например, диагностические тесты (манту все, наверное, делали) или обнаружение сигналов в радиолокации.
Разбирать будем на примере. Все файлы примеров можно скачать в конце статьи. Представим, что вы придумали алгоритм, который определяет присутствие человека на фотографии. Вроде все работает, вы обрадовались, но рано. Нужно ведь оценить качество вашего алгоритма. Тут и нужно использовать наш тест. Не будем сейчас задаваться вопросом о необходимом размере выборки для тестирования. Скажем, что вы взяли 30 фотографий, собственноручно занесли в экселевский файл есть ли на них человек или нет, а затем прогнали через свой алгоритм. В итоге мы получили такую таблицу:
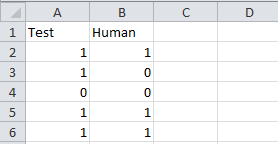
Сохраняем сразу ее в csv, чтобы не напрягаться с чтением xls (это возможно в R, но не из коробки).
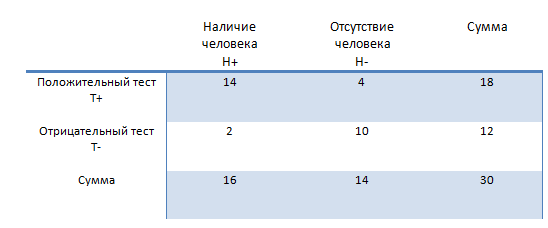
Теперь немного теории. По результатам теста составляется следующая таблица.
Априорная вероятность:
Чувствительность (Sensitivity). P(T+|H+). Вероятность, что человек будет обнаружен.
Se = 14/16
Специфичность (Specificity), в других тестах часто называется мощностью (Power). P(T-|H-). Вероятность того, что при отсутствии человека, результат тест отрицательный.
Sp = 10/14
Отношение правдоподобия (Likelihood quotient). Важная характеристика для оценки теста. Состоит из 2-х значений.
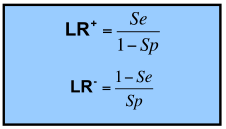
В литературе тест считается хорошим, если LR+ и LR- больше 3 (относится к медицинским тестам).
Апостериорная вероятность: положительное и отрицательное предсказательное значение (positive and negative predictive value). Вероятность, что результат теста (положительный или отрицательный) верен.
PV+ = 14/18
PV- = 10/12
Также существуют такие понятия, как ошибка первого рода (1 — Se) и ошибка второго рода (1 — Sp). По сути эквивалентны sensitivity и specificity.
Для начала загрузка данных.
В двух последних строчках мы присвоили вместо 0 и 1 ярлыки. Необходимо это сделать, т.к. иначе R будет работать с нашими даннами как с числами.
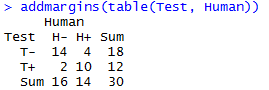
Таблицу можно вывести следующим образом:
Данная таблица неплохая, но существует пакет prettyR, который сделает практически все за нас. Для того, чтобы установить пакет, в дефолтном R gui нужно в packages нажать install packages и набрать имя пакета.
Используем библиотеку. Для разнообразия мы выведем результат в html, т.к. у меня в RStudio таблицы отображаются немного некорректно (если знаете как пофиксить — пишите).

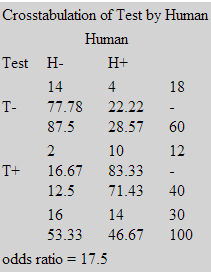
Разберем, что там написано.
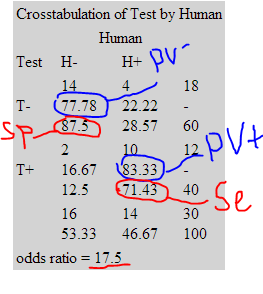
Таким образом, мы получаем количественные характеристики работы нашего алгоритма. Заметим, что LR+, который на таблице обозначен как odds ratio больше 3-х. Также обратим внимание на параметры описанные выше. Как правило, основной интерес должен представлять PV+ и Se, т.к. ложная тревога это дополнительные затраты, а необнаружение может привести к фатальным последствиям.
А что если наши данные являются количественными? Это может быть, например, параметр, по которому предыдущий алгоритм выносит решение (скажем, количество пикселей цвета кожи). Ради интереса, давайте рассмотрим работу алгоритма, который блокирует спамеров.
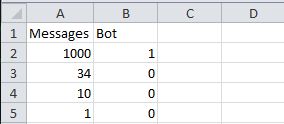
Вы создатель новой социальной сети, и пытаетесь бороться со спамерами. Спамеры посылают большое количество писем, поэтому самое простое — блокировать их после превышения некоторого порога сообщений. Только как его выбрать? Берем выборку из опять 30 пользователей. Узнаем, являются ли они роботами, считываем количество сообщений и получаем:
Совсем чуть-чуть теории. После выбора порога, мы делим выборку на 2 части и получаем таблицу из 1-го примера. Естественно, наша задача выбрать лучший порог. Однозначного алгоритма нет, т.к. в каждом реальном примере sensitivity и specificity играют разную роль. Однако, есть метод, который помогают принять решение, а также оценивают тест в целом. Этот метод называется ROC-curve, кривая “рабочей характерики приемника”, используемый изначально в радиолокации. Построим ее в R.
Для начала установим пакет ROCR (с ним установятся пакеты gtools, gplots и gdata, если у вас их нет).
Опять загрузка данных.
Теперь строим кривую.
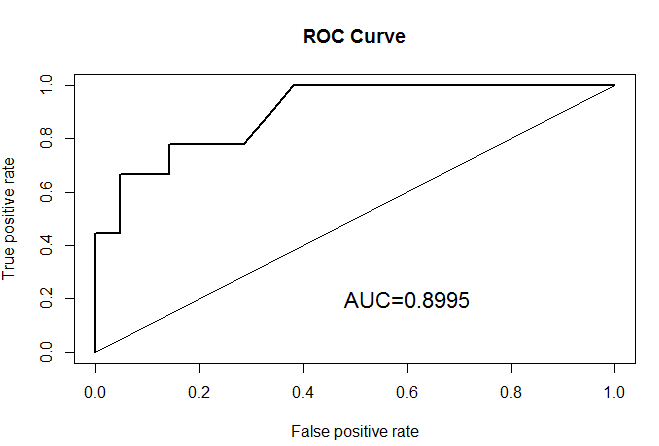
На этом графике по оси y находится sensitivity, а по x (1 — specificity). Очевидно, что для хорошего теста нужно максимизировать и sensitivity и specificity. Неизвестно лишь в какой пропорции. Если оба параметра равнозначны, то можно искать точку, наиболее удаленную от бисектрисы. Кстати, в R есть возможность сделать этот график более наглядным, добавив точки среза.
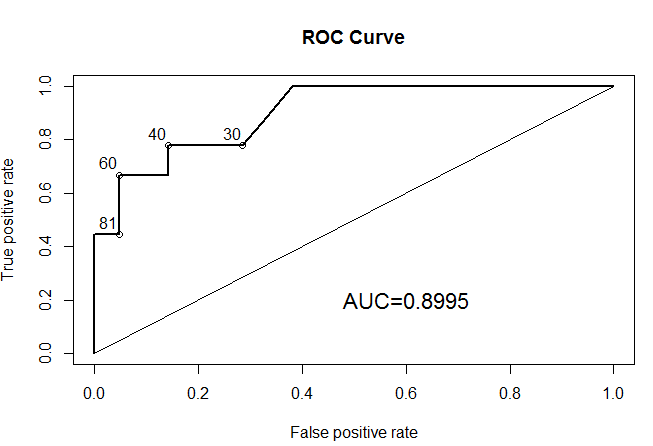
Вот так гораздо лучше. Мы видим, что наиболее удаленные от биссектрисы точки, это 40 и 60. Кстати, о биссектрисе и площади под кривой, которую мы подсчитали. Биссектриса — тест дурака, т.е. 50 на 50. Хороший тест должен иметь площадь под кривой, превышающую площадь 0.5, т.е. площадь под биссектрисой. Желательно сильно превышать, но никак уж не быть меньше, т.к. в этом случае лучше тыкать наугад, чем пользоваться нашим методом.
В данной статье, я описал как работать с бинарной классификацией в R. Как видите, ситуации, где их применить, можно встретить в обычной жизни. Основные характеристики таких тестов: sensivity, specificity, likelihood rate и predictive value. Они связаны между собой и показывают эффективность теста с разных сторон. В случае количественных данных их можно регулировать с помощью выбора точки среза. Для этого можно использовать ROC-curve. Выбор осуществляется отдельно в каждом случае с учетом требований к тесту, но как правило sensitivity важнее.
В следующих статьях речь пойдет об анализе качественных и количественных данных, t-тесте, хи-квадрат тесте и многом другом.
Спасибо за внимание. Надеюсь, вам понравилось!
Файлы примера
Многим из нас приходится сталкиваться с различными данными на работе и в повседневной жизни. Качественно и правильно их обработать и проанализировать не так сложно. В этой серии статей я покажу применения некоторых статистических тестов.
Заинтересовались? Добро пожаловать под кат.
Часть 2: Тесты качественных данных
Часть 3: Тесты количественных данных
Заранее хочу извиниться, что часто использую английские термины, а также за возможный их некорректный перевод.
Бинарная классификация, качественные данные
Первая статья посвящена такому интересному тесту, как бинарная классификация. Это тестирование, которое состоит в проверке объектов на наличие какого-то качества. Например, диагностические тесты (манту все, наверное, делали) или обнаружение сигналов в радиолокации.
Разбирать будем на примере. Все файлы примеров можно скачать в конце статьи. Представим, что вы придумали алгоритм, который определяет присутствие человека на фотографии. Вроде все работает, вы обрадовались, но рано. Нужно ведь оценить качество вашего алгоритма. Тут и нужно использовать наш тест. Не будем сейчас задаваться вопросом о необходимом размере выборки для тестирования. Скажем, что вы взяли 30 фотографий, собственноручно занесли в экселевский файл есть ли на них человек или нет, а затем прогнали через свой алгоритм. В итоге мы получили такую таблицу:

Сохраняем сразу ее в csv, чтобы не напрягаться с чтением xls (это возможно в R, но не из коробки).
Теперь немного теории. По результатам теста составляется следующая таблица.

Важные параметры
Априорная вероятность:
Чувствительность (Sensitivity). P(T+|H+). Вероятность, что человек будет обнаружен.
Se = 14/16
Специфичность (Specificity), в других тестах часто называется мощностью (Power). P(T-|H-). Вероятность того, что при отсутствии человека, результат тест отрицательный.
Sp = 10/14
Отношение правдоподобия (Likelihood quotient). Важная характеристика для оценки теста. Состоит из 2-х значений.

В литературе тест считается хорошим, если LR+ и LR- больше 3 (относится к медицинским тестам).
Апостериорная вероятность: положительное и отрицательное предсказательное значение (positive and negative predictive value). Вероятность, что результат теста (положительный или отрицательный) верен.
PV+ = 14/18
PV- = 10/12
Также существуют такие понятия, как ошибка первого рода (1 — Se) и ошибка второго рода (1 — Sp). По сути эквивалентны sensitivity и specificity.
Теперь в R
Для начала загрузка данных.
tab<-read.csv(file="data1.csv", header=TRUE, sep=",", dec=".")
attach(tab)
Test <- factor(Test, levels=c("0","1"), labels=c("T-","T+"), ordered=T)
Human <-factor(Human, levels=c("0","1"), labels=c("H-","H+"), ordered=T)
В двух последних строчках мы присвоили вместо 0 и 1 ярлыки. Необходимо это сделать, т.к. иначе R будет работать с нашими даннами как с числами.
Таблицу можно вывести следующим образом:
addmargins(table(Test, Human))

Данная таблица неплохая, но существует пакет prettyR, который сделает практически все за нас. Для того, чтобы установить пакет, в дефолтном R gui нужно в packages нажать install packages и набрать имя пакета.
Используем библиотеку. Для разнообразия мы выведем результат в html, т.к. у меня в RStudio таблицы отображаются немного некорректно (если знаете как пофиксить — пишите).
library(prettyR)
test<-calculate.xtab(Test, Human, varnames=c("Test","Human","T+","T-","H+","H-"))
print(test, html=T)


Разберем, что там написано.

Таким образом, мы получаем количественные характеристики работы нашего алгоритма. Заметим, что LR+, который на таблице обозначен как odds ratio больше 3-х. Также обратим внимание на параметры описанные выше. Как правило, основной интерес должен представлять PV+ и Se, т.к. ложная тревога это дополнительные затраты, а необнаружение может привести к фатальным последствиям.
Бинарная классификация, количественные данные
А что если наши данные являются количественными? Это может быть, например, параметр, по которому предыдущий алгоритм выносит решение (скажем, количество пикселей цвета кожи). Ради интереса, давайте рассмотрим работу алгоритма, который блокирует спамеров.
Вы создатель новой социальной сети, и пытаетесь бороться со спамерами. Спамеры посылают большое количество писем, поэтому самое простое — блокировать их после превышения некоторого порога сообщений. Только как его выбрать? Берем выборку из опять 30 пользователей. Узнаем, являются ли они роботами, считываем количество сообщений и получаем:

Совсем чуть-чуть теории. После выбора порога, мы делим выборку на 2 части и получаем таблицу из 1-го примера. Естественно, наша задача выбрать лучший порог. Однозначного алгоритма нет, т.к. в каждом реальном примере sensitivity и specificity играют разную роль. Однако, есть метод, который помогают принять решение, а также оценивают тест в целом. Этот метод называется ROC-curve, кривая “рабочей характерики приемника”, используемый изначально в радиолокации. Построим ее в R.
Для начала установим пакет ROCR (с ним установятся пакеты gtools, gplots и gdata, если у вас их нет).
Опять загрузка данных.
# loading data
# don't forget to set your working directory
tab <- read.csv(file="data2.csv", header=TRUE, sep=",", dec=".")
attach(tab)
Теперь строим кривую.
# area under the curve calculation
auc <- slot(performance(pred, "auc"), "y.values")[[1]]
# ROC-curve
library(ROCR)
pred <- prediction(Messages, Bot)
plot(performance(pred, "tpr", "fpr"),lwd=2)
lines(c(0,1),c(0,1))
text(0.6,0.2,paste("AUC=", round(auc,4), sep=""), cex=1.4)
title("ROC Curve")

На этом графике по оси y находится sensitivity, а по x (1 — specificity). Очевидно, что для хорошего теста нужно максимизировать и sensitivity и specificity. Неизвестно лишь в какой пропорции. Если оба параметра равнозначны, то можно искать точку, наиболее удаленную от бисектрисы. Кстати, в R есть возможность сделать этот график более наглядным, добавив точки среза.
# ROC-curve with better plotting
plot(performance(pred, "tpr", "fpr"), print.cutoffs.at=c(30,40,60,81), text.adj=c(1.1,-0.5) ,lwd=2)
lines(c(0,1),c(0,1))
text(0.6,0.2,paste("AUC=", round(auc,4), sep=""), cex=1.4)
title("ROC Curve")

Вот так гораздо лучше. Мы видим, что наиболее удаленные от биссектрисы точки, это 40 и 60. Кстати, о биссектрисе и площади под кривой, которую мы подсчитали. Биссектриса — тест дурака, т.е. 50 на 50. Хороший тест должен иметь площадь под кривой, превышающую площадь 0.5, т.е. площадь под биссектрисой. Желательно сильно превышать, но никак уж не быть меньше, т.к. в этом случае лучше тыкать наугад, чем пользоваться нашим методом.
Итоги
В данной статье, я описал как работать с бинарной классификацией в R. Как видите, ситуации, где их применить, можно встретить в обычной жизни. Основные характеристики таких тестов: sensivity, specificity, likelihood rate и predictive value. Они связаны между собой и показывают эффективность теста с разных сторон. В случае количественных данных их можно регулировать с помощью выбора точки среза. Для этого можно использовать ROC-curve. Выбор осуществляется отдельно в каждом случае с учетом требований к тесту, но как правило sensitivity важнее.
В следующих статьях речь пойдет об анализе качественных и количественных данных, t-тесте, хи-квадрат тесте и многом другом.
Спасибо за внимание. Надеюсь, вам понравилось!
Файлы примера