 Привет. В этом посте мы проведем эксперимент, в котором протестируем два типа регуляризации в ограниченной машине Больцмана. Как оказалось, RBM очень чувствительна к параметрам модели, таким как момент и локальное поле нейрона (более подробно обо всех параметрах можно прочитать в практическом руководстве в RBM Джеффри Хинтона). Но мне для полной картины и для получения шаблонов наподобие таких вот, не хватало еще одного параметра — регуляризации. К ограниченным машинам Больцмана можно относиться и как к разновидности сети Маркова, и как к очередной нейроной сети, но если копнуть глубже, то будет видна аналогия и со зрением. Подобно первичной зрительной коре, получающей информацию от сетчатки через зрительный нерв (да простят меня биологи за такое упрощение), RBM ищет простые шаблоны во входном изображении. На этом аналогия не заканчивается, если очень малые и нулевые веса интерпретировать как отсутствие веса, то мы получим, что каждый скрытый нейрон RBM формирует некоторое рецептивное поле, а сформированная из обученных RBM глубокая сеть формирует из простых образов более комплексные признаки; чем-то подобным, в принципе, и занимается зрительная кора головного мозга, правда, вероятно, как то посложнее =)
Привет. В этом посте мы проведем эксперимент, в котором протестируем два типа регуляризации в ограниченной машине Больцмана. Как оказалось, RBM очень чувствительна к параметрам модели, таким как момент и локальное поле нейрона (более подробно обо всех параметрах можно прочитать в практическом руководстве в RBM Джеффри Хинтона). Но мне для полной картины и для получения шаблонов наподобие таких вот, не хватало еще одного параметра — регуляризации. К ограниченным машинам Больцмана можно относиться и как к разновидности сети Маркова, и как к очередной нейроной сети, но если копнуть глубже, то будет видна аналогия и со зрением. Подобно первичной зрительной коре, получающей информацию от сетчатки через зрительный нерв (да простят меня биологи за такое упрощение), RBM ищет простые шаблоны во входном изображении. На этом аналогия не заканчивается, если очень малые и нулевые веса интерпретировать как отсутствие веса, то мы получим, что каждый скрытый нейрон RBM формирует некоторое рецептивное поле, а сформированная из обученных RBM глубокая сеть формирует из простых образов более комплексные признаки; чем-то подобным, в принципе, и занимается зрительная кора головного мозга, правда, вероятно, как то посложнее =)L1 и L2 регуляризация
Начнем мы, пожалуй, с краткого описания того, что такое регуляризация модели — это способ наложить штраф к целевой функции за сложность модели. С байесовской точки зрения — это способ учесть некоторую априорную информацию о распределении параметров модели. Важным свойством является то, что регуляризация помогает избежать переобучения модели. Обозначим параметры модели как θ = {θ_i}, i=1..n. Итоговая целевая функция C = η(E + λR), где E — это основная целевая функция модели, R = R(θ) — функция от параметров модели, эта и лямбда — это скорость обучения и параметр регуляризации соответственно. Таким образом, для вычисления градиента итоговой целевой функции будет необходимо вычислить градиент функции регуляризации:
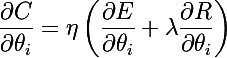
Мы рассмотрим два вида регуляризации, корни которых находятся в Lp метрике. Функция регуляризации L1 и ее производные имеют следующий вид:
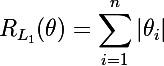
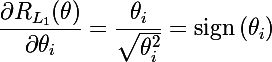
L2 регулярицазия выглядит следующим образом:
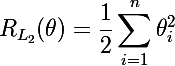
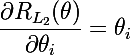
Оба метода регуляризации штрафуют модель за большое значение весов, в первом случае абсолютными значениями весов, во втором квадратами весов, таким образом, распределение весов будет приближаться к нормальному с центром в нуле и большим пиком. Более подробное сравнение L1 и L2 можно почитать тут. Как мы позже увидим, около 70% весов будут меньше 10^(-8).
Регуляризация в RBM
В позапрошлом посте я описывал пример реализации RBM на C#. Я буду опираться на ту же реализацию для того, чтобы показать, куда встраивается регуляризация, но сначала формулы. Целью обучения RBM является максимизация вероятности того, что восстановленный образ будет идентичен входному:

Вообще говоря, в алгоритме максимизируется логарифм вероятности, и чтобы внести штраф, необходимо вычесть значение функции регуляризации из полученной вероятности, в итоге новая целевая функция приобретает следующий вид:
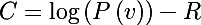
Производная такой функции по параметру будет выглядить так:

Алгоритм contrastive divergence состоит из положительной фазы и отрицательной, таким образом, для того, чтобы добавить регуляризацию, достаточно вычесть значение производной функции регуляризации и из значения положительной фазы, после вычитания отрицательной фазы:
positive and negative phases
#region Gibbs sampling
for (int k = 0; k <= _config.GibbsSamplingChainLength; k++)
{
//calculate hidden states probabilities
hiddenLayer.Compute();
#region accumulate negative phase
if (k == _config.GibbsSamplingChainLength)
{
for (int i = 0; i < visibleLayer.Neurons.Length; i++)
{
for (int j = 0; j < hiddenLayer.Neurons.Length; j++)
{
nablaWeights[i, j] -= visibleLayer.Neurons[i].LastState *
hiddenLayer.Neurons[j].LastState;
if (_config.RegularizationFactor > Double.Epsilon)
{
//regularization of weights
double regTerm = 0;
switch (_config.RegularizationType)
{
case RegularizationType.L1:
regTerm = _config.RegularizationFactor*
Math.Sign(visibleLayer.Neurons[i].Weights[j]);
break;
case RegularizationType.L2:
regTerm = _config.RegularizationFactor*
visibleLayer.Neurons[i].Weights[j];
break;
}
nablaWeights[i, j] -= regTerm;
}
}
}
if (_config.UseBiases)
{
for (int i = 0; i < hiddenLayer.Neurons.Length; i++)
{
nablaHiddenBiases[i] -= hiddenLayer.Neurons[i].LastState;
}
for (int i = 0; i < visibleLayer.Neurons.Length; i++)
{
nablaVisibleBiases[i] -= visibleLayer.Neurons[i].LastState;
}
}
break;
}
#endregion
//sample hidden states
for (int i = 0; i < hiddenLayer.Neurons.Length; i++)
{
hiddenLayer.Neurons[i].LastState = _r.NextDouble() <= hiddenLayer.Neurons[i].LastState ? 1d : 0d;
}
#region accumulate positive phase
if (k == 0)
{
for (int i = 0; i < visibleLayer.Neurons.Length; i++)
{
for (int j = 0; j < hiddenLayer.Neurons.Length; j++)
{
nablaWeights[i, j] += visibleLayer.Neurons[i].LastState*
hiddenLayer.Neurons[j].LastState;
}
}
if (_config.UseBiases)
{
for (int i = 0; i < hiddenLayer.Neurons.Length; i++)
{
nablaHiddenBiases[i] += hiddenLayer.Neurons[i].LastState;
}
for (int i = 0; i < visibleLayer.Neurons.Length; i++)
{
nablaVisibleBiases[i] += visibleLayer.Neurons[i].LastState;
}
}
}
#endregion
//calculate visible probs
visibleLayer.Compute();
}
#endregion
}
#endregion
Переходим к экспериментам. В качестве тестовых данных использовался тот же набор, что и в позапрошлом посте. Во всех случаях обучение проводилось ровно 1000 эпох. Я буду приводить два способа визуализации найденных шаблонов, в первом случае (рисунок в серых тонах) темное значение соответствует минимальному значению веса, а белый максимальному; во втором рисунке черный соответствует нулю, увеличение красной составляющей соответствует увеличению в положительную сторону, а увеличение синей составляющей — в отрицательную. Так же я буду приводить гистограмму распределения весов и небольшие комментарии.
Без регуляризации


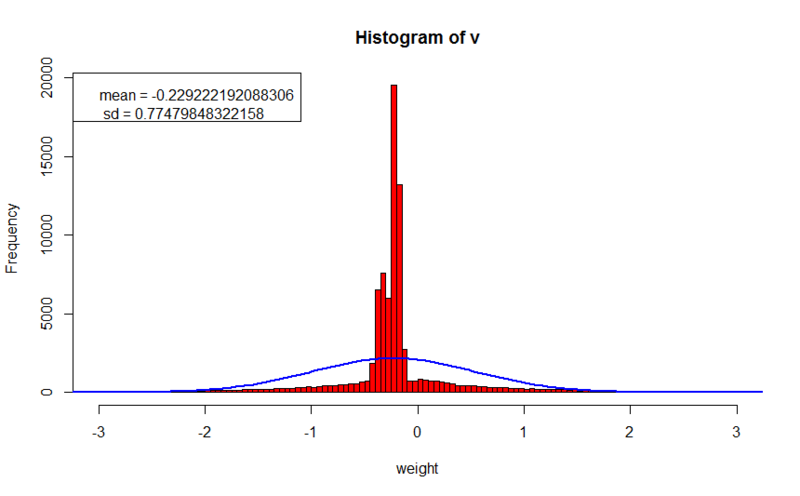
- значение ошибки на обучающем наборе: 0.188181367765024
- значение ошибки на кроссвалидационном наборе: 21.0910315518859
Шаблоны получились очень размытые, и трудно анализируемые. Среднее значение весов сдвинуто влево, а абсолютное значение весов достигает 2 и более.
L2 регуляризация


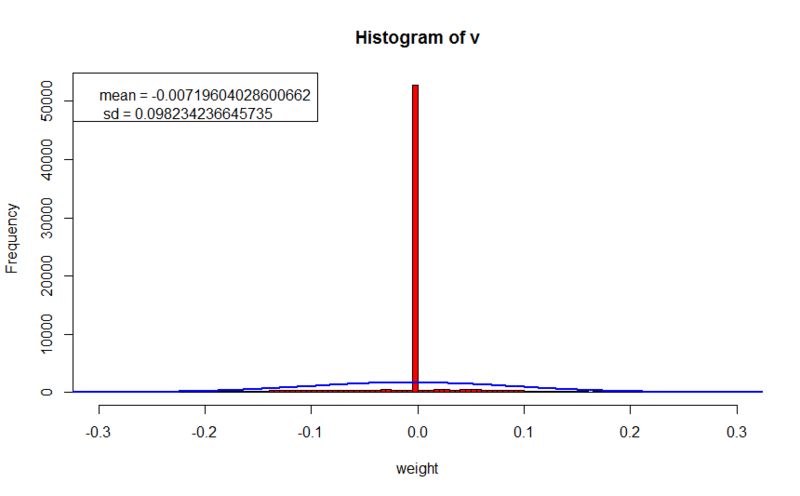
- значение ошибки на обучающем наборе: 10.1198906337165
- значение ошибки на кроссвалидационном наборе: 23.3600809429977
- параметр регуляризации: 0.1
Здесь мы наблюдаем более четкие образы. Мы уже можем разглядеть, что на некоторых образах действительно учитываются какие-то особенности букв. Несмотря на то, что ошибка на обучающем наборе в 100 раз хуже, чем при обучении без регуляризации, ошибка на кроссвалидационном множестве не намного превышает первый эксперимент, что говорит о том, что обобщающая способность сети на незнакомых образах не сильно ухудшилась (стоит заметить, что в подсчет ошибки не включалось значение функции регуляризации, что позволяет нам сравнивать значения с предыдущем опытом). Веса сконцентрированы вокруг нуля, и не сильно превышают 0.2 по абсолютному значению, что в 10 раз меньше, чем в предыдущем опыте.
L1 регуляризация


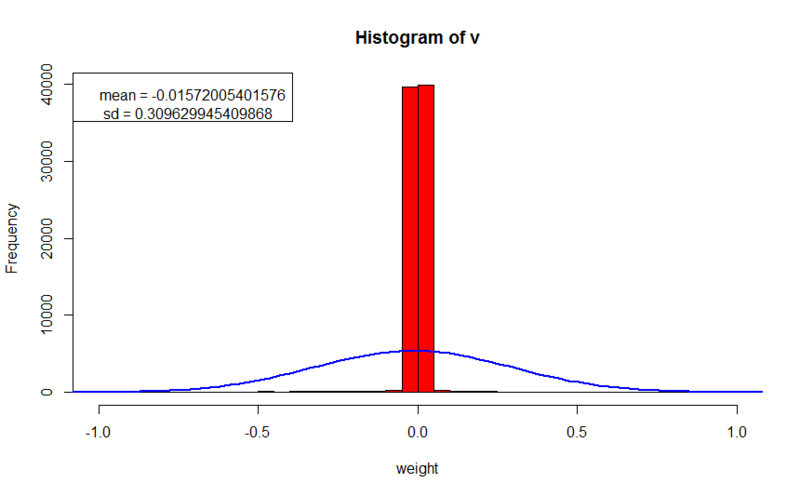
- значение ошибки на обучающем наборе: 4.42672814826447
- значение ошибке на кроссвалидационном наборе: 17.3700437102876
- параметр регуляризации: 0.005
В данном опыте мы наблюдаем четкие шаблоны, а в особенности рецептивные поля (вокруг сине-красных пятен все веса почти равны нулю). Шаблоны даже поддаются анализу, мы можем заметить, например, ребра от W (первый ряд четвертая картинка), или же шаблон, который отражает средний размер входных образов (в пятом ряду 8 и 10 картинка). Ошибка восстановления на обучающем множестве в 40 раз хуже чем в первом эксперименте, но лучше чем при L2 регуляризации, в то же время ошибка на неизвестном множестве лучше, чем в обоих предыдущих опытах, что говорит о еще лучшей обобщающей способности. Веса так же сконцентрированы вокруг нуля, и в большинстве случаев не сильно его превышают. Существенное отличие в параметре регуляризации объясняется тем, что при вычислении градиента для L2 параметр умножается на значение веса, как правило эти оба числа меньше 1; но при L1 параметр умножается на |1|, и и итоговое значение будет того же порядка что и параметр регуляризации.
Заключение
В качестве заключения хочется сказать что РБМ действительно очень чувствительная к параметрам вещь. И главное — не сломаться в процессе поиска решения -) В конце приведу увеличенное излбражение одной из RBM тренировавшихся с L1 регуляризацией, но уже в течении 5000 эпох.

UPDATE:
недавно обучил рбм на полном наборе больших букв 4 шрифтов 3 стилей, в течении 5000 итераций с L1 регуляризацией, это заняло около 14 часов, но результат еще интереснее, фичи получились еще более локальные и чистые

