Сегодня – вторая серия цикла, начатого в прошлый раз; тогда мы поговорили о направленных графических вероятностных моделях, нарисовали главные картинки этой науки и обсудили, каким зависимостям и независимостям они соответствуют. Сегодня – ряд иллюстраций к материалу прошлого раза; мы обсудим несколько важных и интересных моделей, нарисуем соответствующие им картинки и увидим, каким факторизациям совместного распределения всех переменных они соответствуют.

Начну с того, что кратко повторю прошлый текст: мы уже говорили о наивном байесовском классификаторе в этом блоге. В наивном байесе делается дополнительное предположение об условной независимости атрибутов (слов) при условии темы:
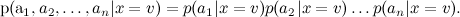
В результате сложное апостериорное распределение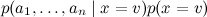 удалось переписать как
удалось переписать как
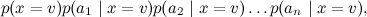
И вот какая картинка этой модели соответствует:
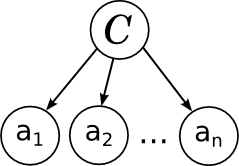
Всё в точности как мы говорили в прошлый раз: отдельные слова в документе связаны с переменной категории расходящейся связью; это показывает, что они условно независимы при условии данной категории. Обучение наивного байеса заключается в том, чтобы обучить параметры отдельных факторов: априорного распределения на категориях p(C) и условных распределений отдельных параметров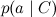 .
.
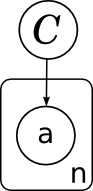
Ещё одно замечание о картинках, прежде чем двигаться дальше. Очень часто в моделях встречается большое число однотипных переменных, которые связаны с другими переменными одними и теми же распределениями (возможно, с разными параметрами). Чтобы картинку легче было читать и понимать, чтобы в ней не было бесчисленных многоточий и вещей типа «ну а тут полный двудольный граф с многоточиями, ну, вы понимаете», удобно объединять однотипные переменные в так называемые «плашки» (plates). Для этого рисуют прямоугольник, в который помещают одного типичного представителя размножаемой переменной; где-нибудь в углу прямоугольника удобно ещё подписать, сколько копий подразумевается:
А общая модель всех документов (без плашек мы её не рисовали) будет состоять из нескольких копий этого графа и, соответственно, выглядеть так:
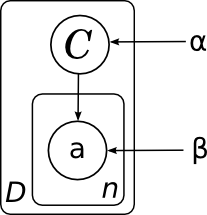
Здесь я явным образом нарисовал параметры распределения на категориях α и параметры – вероятности слов в каждой категории β. Поскольку у этих параметров нет отдельного фактора в разложении, им не соответствует узел сети, но часто удобно их тоже изобразить для наглядности. В данном случае картинка означает, что разные копии переменной C были порождены из одного и того же распределения p(C), а разные копии слов порождались из одного и того же распределения, параметризованного ещё и значением категорий (т.е. β – это матрица вероятностей разных слов в разных категориях).
Продолжим ещё одной моделью, которую вы, возможно, смутно припоминаете из курсов матстатистики – линейной регрессией. Суть модели проста: мы предполагаем, что переменная y, которую мы хотим предсказать, получается из вектора признаков x как некоторая линейная функция с весами w (жирный шрифт будет обозначать векторы – это и общепринято, и в html мне это будет удобнее, чем каждый раз рисовать стрелочку) и нормально распределённым шумом:
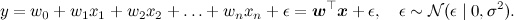
В модели предполагается, что нам доступен некоторый набор данных, датасет D. Он состоит из отдельных реализаций этой самой регрессии, и (важно!) предполагается, что эти реализации были порождены независимо. Кроме того, в линейной регрессии часто вводят априорное распределение на параметры – например, нормальное распределение
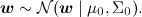
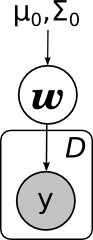
Тогда мы приходим к вот такой картинке:
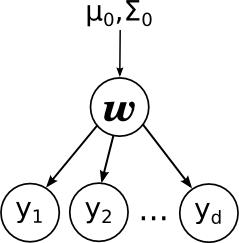
Здесь я явным образом нарисовал параметры априорного распределения μ0 и Σ0. Обратите внимание – линейная регрессия очень похожа по структуре на наивный байес.
С плашками то же самое будет выглядеть ещё проще:
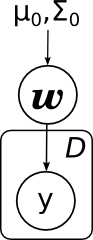
Какие основные задачи, которые решаются в линейной регрессии? Первая задача – найти апостериорное распределение на w, т.е. научиться пересчитывать распределение w при имеющихся данных (x,y) из D; математически мы должны посчитать параметры распределения
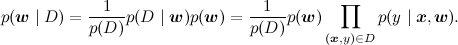
В графических моделях обычно заштриховывают переменные, значения которых известны; таким образом, задача состоит в том, чтобы по вот такому графу со свидетельствами пересчитать распределение w:
Вторая основная задача (в чём-то даже более основная) – посчитать предсказательное распределение, оценить новое значение y в какой-то новой точке. Математически эта задача выглядит существенно сложнее, чем предыдущая – теперь надо интегрировать по апостериорному распределению
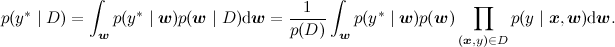
А графически как раз меняется не так много – мы рисуем новую переменную, которую хотим предсказывать, а задача по-прежнему та же: с некоторыми свидетельствами (из датасета) пересчитать распределение некоторой другой переменной в модели, только теперь это не w, а y*:

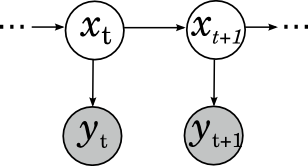
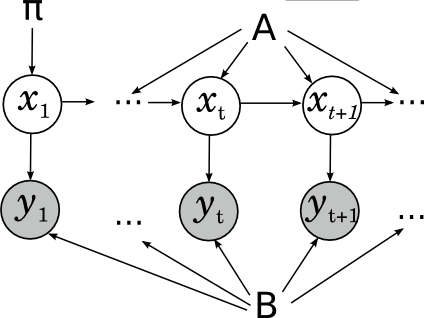
Ещё один широко известный и популярный класс вероятностных моделей – скрытые марковские модели (hidden Markov models, HMM). Они применяются в распознавании речи, для нечёткого поиска подстрок и в других тому подобных приложениях. Скрытая марковская модель – это марковская цепь (последовательность случайных величин, где каждая величина xt+1 зависит только от предыдущей xt и при условии xt условно независима с предыдущими xt-k), в которой мы не можем наблюдать скрытые состояния, а видим только некоторые наблюдаемые yt, которые зависят от текущего состояния. Например, в распознавании речи скрытые состояния – это фонемы, которые вы хотите сказать (это некоторое упрощение, на самом деле каждая фонема – это целая модель, но для иллюстрации сойдёт), а наблюдаемые – это собственно звуковые волны, которые доходят до распознающего устройства. Картинка получается вот какая:
Этой картинки достаточно, чтобы решать задачу применения уже готовой скрытой марковской модели: по имеющейся модели (состоящей из вероятностей перехода между скрытыми состояниями A, начального распределения цепи π и параметров распределений наблюдаемых B) и данной последовательности наблюдаемых найти наиболее вероятную последовательность скрытых состояний; т.е., например, в уже готовой системе распознавания речи распознать новый звуковой файл. А если нужно обучить параметры модели, лучше явно нарисовать их и на картинке, чтобы было понятно, что одни и те же параметры участвуют во всех переходах:
Ещё одна модель, о которой мы уже говорили – LDA (latent Dirichlet allocation, латентное размещение Дирихле). Это модель для тематического моделирования, в которой каждый документ представляется не одной темой, как в наивном байесе, а дискретным распределением на возможных темах. В том же тексте мы уже приводили описание генеративной модели LDA – как породить документ в готовой модели LDA:
Теперь мы понимаем, как будет выглядеть соответствующая картинка (она тоже была в том блогпосте, и я опять скопирую её из википедии, но суть картинки здесь точно такая же, как у нас выше):

В целой серии постов (1, 2, 3, 4) мы говорили об одном из главных инструментов коллаборативной фильтрации – сингулярном разложении матриц, SVD.
Мы искали SVD-разложение методом градиентного спуска: конструировали функцию ошибки, считали от неё градиент, спускались по нему. Однако можно сформулировать и общую вероятностную постановку задачи, которая обычно называется PMF (probabilistic matrix factorization). Для этого нужно ввести априорные распределения на векторы признаков пользователей и продуктов:
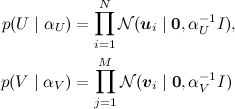
(где I – единичная матрица), а затем, как в обычном SVD, представить рейтинги как зашумленные линейные комбинации признаков пользователей и продуктов:
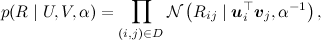
где произведение берётся по рейтингам, присутствующим в обучающей выборке. Получается вот такая картинка (картинка взята из статьи [Salakhutdinov, Mnih, 2009]):
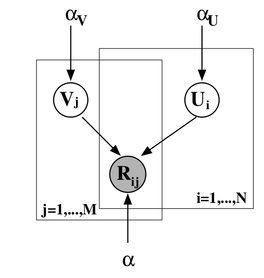
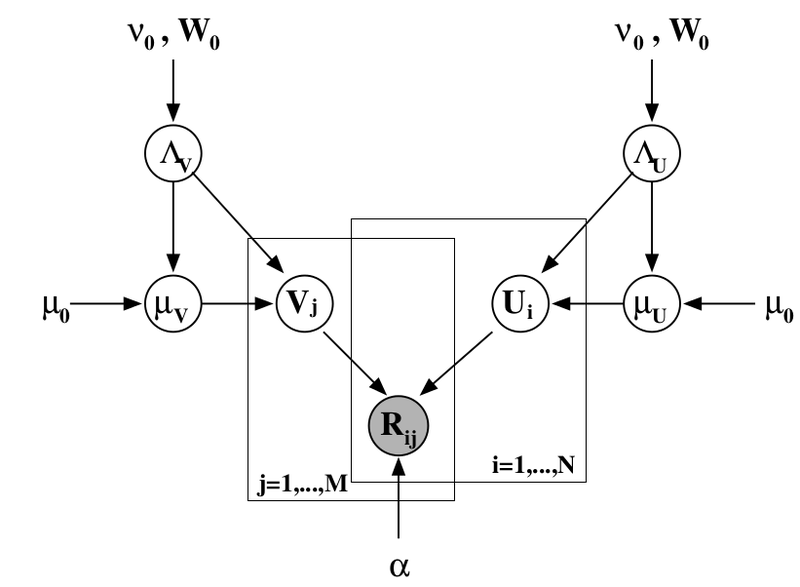
Можно добавить ещё один уровень байесовского вывода и обучать заодно и гиперпараметры распределений признаков для пользователей и продуктов; я сейчас не буду в это углубляться, а просто приведу соответствующую картинку (из той же статьи) – возможно, ещё доведётся поговорить об этом подробнее.
Ещё один пример, который лично мне близок – когда-то мы с Александром Сироткиным улучшили одну из байесовских рейтинг-систем; возможно, позднее в блоге мы поговорим о рейтинг-системах подробнее. Но здесь я просто приведу простейший пример – как работает рейтинг Эло для шахматистов? Если не вдаваться в аппроксимации и магические константы, суть очень простая: что такое вообще рейтинг? Мы хотели бы, чтобы рейтинг был мерилом силы игры; однако при этом совершенно очевидно, что сила игры от партии к партии может достаточно сильно меняться под воздействием внешних и внутренних случайных факторов. Таким образом, на самом деле сила игры того или иного участника в конкретной партии (сравнение этих сил и определяет исход партии) – это случайная величина, «истинная сила» игры шахматиста – её математическое ожидание, а рейтинг – это наша неточная оценка этого математического ожидания. Мы пока будем рассматривать простейший случай, в котором сила игры участника в конкретной партии нормально распределена вокруг его истинной силы с некоторой постоянной заранее фиксированной дисперсией (рейтинг Эло именно так и делает – отсюда и его магическая константа «шахматист с силой на 200 пунктов рейтинга больше набирает в среднем 0.75 очка за партию»). Перед каждой партией мы имеем некоторые априорные оценки силы игры каждого шахматиста; предположим, что априорное распределение тоже нормальное, с параметрами μ1, σ1 и μ2, σ2 соответственно. Наша задача – зная результат партии, пересчитать эти параметры. Картинка получается вот какая:
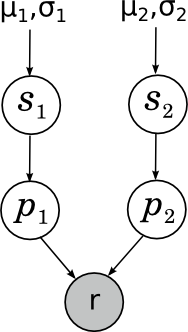
Здесь si (skill) – «истинная сила игры» шахматиста, pi (performance) – его сила игры, показанная в данной конкретной партии, а r – довольно интересно устроенная случайная переменная, показывающая результат партии, который получается из сравнения p1 и p2. Подробнее об этом сегодня не будем.
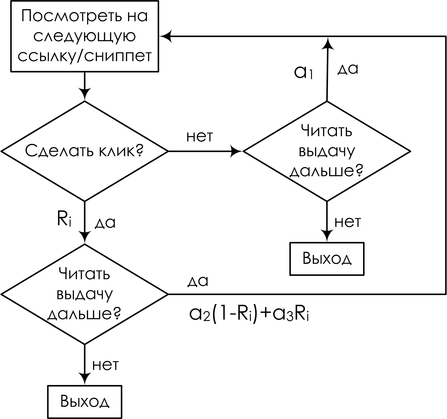
И закончу ещё одним близким мне примером – моделями поведения интернет-пользователей в поисковых системах. Опять же, подробно вдаваться не буду – может быть, ещё вернёмся к этому, а пока можно почитать, например, нашу с Александром Фишковым обзорную статью – просто рассмотрю одну такую модель для примера. Мы пытаемся смоделировать, что делает пользователь, когда получает поисковую выдачу. Просмотр ссылки и клик трактуются как случайные события; для конкретной запросной сессии переменная Ei обозначает просмотр описания ссылки на документ, показанный на позиции i, Ci – клик на этой позиции. Введём упрощающее предположение: предположим, что процесс просмотра описаний всегда начинается с первой позиции и строго линеен. Позиция просматривается, только если все предыдущие позиции были просмотрены. В итоге наш виртуальный пользователь читает ссылки сверху вниз, если ему понравился (что зависит от релевантности ссылки), кликает, и, если документ действительно оказывается релевантным, пользователь уходит и больше не возвращается; любопытно, но факт: для поисковой системы хорошее событие – это когда пользователь как можно быстрее ушёл и не вернулся, а если он возвращается к выдаче, значит, не смог найти то, что искал.
В результате получается так называемая каскадная клик-модель (cascading click model, CCM); в ней пользователь следует вот такой блок-схеме:
А в виде байесовской сети это можно нарисовать вот так:
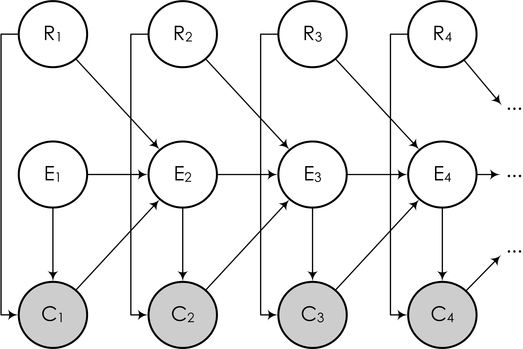
Здесь последующие события Ei (это событие «пользователь прочитал следующий сниппет», от слова examine) зависят от того, был ли клик на предыдущей ссылке, и если был, то оказалась ли ссылка действительно релевантной. Задача же снова описывается так же, как выше: мы наблюдаем часть переменных (клики пользователя), и должны на основании кликов обучить модель и сделать выводы о релевантности каждой ссылки (для того чтобы в дальнейшем переупорядочивать ссылки согласно их истинной релевантности), т.е. о значениях некоторых других переменных в модели.
В этой статье мы рассмотрели несколько примеров вероятностных моделей, логика которых легко «считывается» из их направленных графических моделей. Кроме того, мы убедились: то, чего мы обычно хотим от вероятностной модели, можно представить в виде одной достаточно хорошо определённой задачи – в направленной графической модели пересчитать распределение одних переменных при известных значениях некоторых других переменных. Однако логика логикой, а как, собственно, обучать? Как решать эту задачу? Об этом – в следующих сериях.

Наивный байесовский классификатор
Начну с того, что кратко повторю прошлый текст: мы уже говорили о наивном байесовском классификаторе в этом блоге. В наивном байесе делается дополнительное предположение об условной независимости атрибутов (слов) при условии темы:
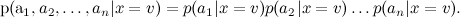
В результате сложное апостериорное распределение
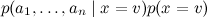 удалось переписать как
удалось переписать как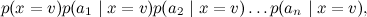
И вот какая картинка этой модели соответствует:
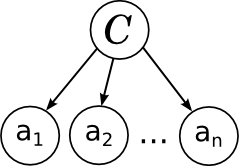
Всё в точности как мы говорили в прошлый раз: отдельные слова в документе связаны с переменной категории расходящейся связью; это показывает, что они условно независимы при условии данной категории. Обучение наивного байеса заключается в том, чтобы обучить параметры отдельных факторов: априорного распределения на категориях p(C) и условных распределений отдельных параметров
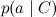 .
.Ещё одно замечание о картинках, прежде чем двигаться дальше. Очень часто в моделях встречается большое число однотипных переменных, которые связаны с другими переменными одними и теми же распределениями (возможно, с разными параметрами). Чтобы картинку легче было читать и понимать, чтобы в ней не было бесчисленных многоточий и вещей типа «ну а тут полный двудольный граф с многоточиями, ну, вы понимаете», удобно объединять однотипные переменные в так называемые «плашки» (plates). Для этого рисуют прямоугольник, в который помещают одного типичного представителя размножаемой переменной; где-нибудь в углу прямоугольника удобно ещё подписать, сколько копий подразумевается:

А общая модель всех документов (без плашек мы её не рисовали) будет состоять из нескольких копий этого графа и, соответственно, выглядеть так:
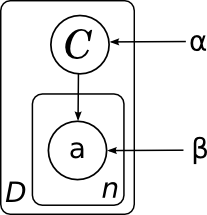
Здесь я явным образом нарисовал параметры распределения на категориях α и параметры – вероятности слов в каждой категории β. Поскольку у этих параметров нет отдельного фактора в разложении, им не соответствует узел сети, но часто удобно их тоже изобразить для наглядности. В данном случае картинка означает, что разные копии переменной C были порождены из одного и того же распределения p(C), а разные копии слов порождались из одного и того же распределения, параметризованного ещё и значением категорий (т.е. β – это матрица вероятностей разных слов в разных категориях).
Линейная регрессия
Продолжим ещё одной моделью, которую вы, возможно, смутно припоминаете из курсов матстатистики – линейной регрессией. Суть модели проста: мы предполагаем, что переменная y, которую мы хотим предсказать, получается из вектора признаков x как некоторая линейная функция с весами w (жирный шрифт будет обозначать векторы – это и общепринято, и в html мне это будет удобнее, чем каждый раз рисовать стрелочку) и нормально распределённым шумом:
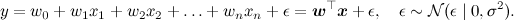
В модели предполагается, что нам доступен некоторый набор данных, датасет D. Он состоит из отдельных реализаций этой самой регрессии, и (важно!) предполагается, что эти реализации были порождены независимо. Кроме того, в линейной регрессии часто вводят априорное распределение на параметры – например, нормальное распределение
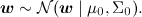
Тогда мы приходим к вот такой картинке:

Здесь я явным образом нарисовал параметры априорного распределения μ0 и Σ0. Обратите внимание – линейная регрессия очень похожа по структуре на наивный байес.
С плашками то же самое будет выглядеть ещё проще:
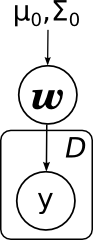
Какие основные задачи, которые решаются в линейной регрессии? Первая задача – найти апостериорное распределение на w, т.е. научиться пересчитывать распределение w при имеющихся данных (x,y) из D; математически мы должны посчитать параметры распределения
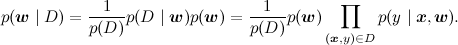
В графических моделях обычно заштриховывают переменные, значения которых известны; таким образом, задача состоит в том, чтобы по вот такому графу со свидетельствами пересчитать распределение w:
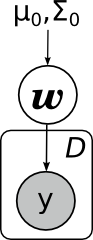
Вторая основная задача (в чём-то даже более основная) – посчитать предсказательное распределение, оценить новое значение y в какой-то новой точке. Математически эта задача выглядит существенно сложнее, чем предыдущая – теперь надо интегрировать по апостериорному распределению
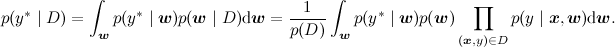
А графически как раз меняется не так много – мы рисуем новую переменную, которую хотим предсказывать, а задача по-прежнему та же: с некоторыми свидетельствами (из датасета) пересчитать распределение некоторой другой переменной в модели, только теперь это не w, а y*:

Скрытые марковские модели
Ещё один широко известный и популярный класс вероятностных моделей – скрытые марковские модели (hidden Markov models, HMM). Они применяются в распознавании речи, для нечёткого поиска подстрок и в других тому подобных приложениях. Скрытая марковская модель – это марковская цепь (последовательность случайных величин, где каждая величина xt+1 зависит только от предыдущей xt и при условии xt условно независима с предыдущими xt-k), в которой мы не можем наблюдать скрытые состояния, а видим только некоторые наблюдаемые yt, которые зависят от текущего состояния. Например, в распознавании речи скрытые состояния – это фонемы, которые вы хотите сказать (это некоторое упрощение, на самом деле каждая фонема – это целая модель, но для иллюстрации сойдёт), а наблюдаемые – это собственно звуковые волны, которые доходят до распознающего устройства. Картинка получается вот какая:

Этой картинки достаточно, чтобы решать задачу применения уже готовой скрытой марковской модели: по имеющейся модели (состоящей из вероятностей перехода между скрытыми состояниями A, начального распределения цепи π и параметров распределений наблюдаемых B) и данной последовательности наблюдаемых найти наиболее вероятную последовательность скрытых состояний; т.е., например, в уже готовой системе распознавания речи распознать новый звуковой файл. А если нужно обучить параметры модели, лучше явно нарисовать их и на картинке, чтобы было понятно, что одни и те же параметры участвуют во всех переходах:

LDA
Ещё одна модель, о которой мы уже говорили – LDA (latent Dirichlet allocation, латентное размещение Дирихле). Это модель для тематического моделирования, в которой каждый документ представляется не одной темой, как в наивном байесе, а дискретным распределением на возможных темах. В том же тексте мы уже приводили описание генеративной модели LDA – как породить документ в готовой модели LDA:
- выбрать длину документа N (этого на графе не нарисовано – это не то чтобы часть модели);
- выбрать вектор
 — вектор «степени выраженности» каждой темы в этом документе;
— вектор «степени выраженности» каждой темы в этом документе; - для каждого из N слов w:
- выбрать тему
 по распределению
по распределению  ;
; - выбрать слово
 с вероятностями, заданными в β.
с вероятностями, заданными в β.
- выбрать тему
Теперь мы понимаем, как будет выглядеть соответствующая картинка (она тоже была в том блогпосте, и я опять скопирую её из википедии, но суть картинки здесь точно такая же, как у нас выше):

SVD и PMF
В целой серии постов (1, 2, 3, 4) мы говорили об одном из главных инструментов коллаборативной фильтрации – сингулярном разложении матриц, SVD.
Мы искали SVD-разложение методом градиентного спуска: конструировали функцию ошибки, считали от неё градиент, спускались по нему. Однако можно сформулировать и общую вероятностную постановку задачи, которая обычно называется PMF (probabilistic matrix factorization). Для этого нужно ввести априорные распределения на векторы признаков пользователей и продуктов:
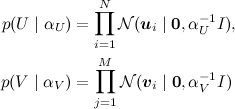
(где I – единичная матрица), а затем, как в обычном SVD, представить рейтинги как зашумленные линейные комбинации признаков пользователей и продуктов:
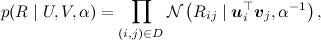
где произведение берётся по рейтингам, присутствующим в обучающей выборке. Получается вот такая картинка (картинка взята из статьи [Salakhutdinov, Mnih, 2009]):
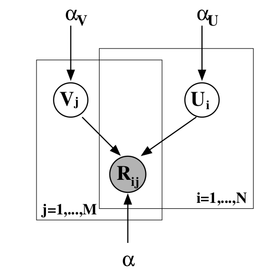
Можно добавить ещё один уровень байесовского вывода и обучать заодно и гиперпараметры распределений признаков для пользователей и продуктов; я сейчас не буду в это углубляться, а просто приведу соответствующую картинку (из той же статьи) – возможно, ещё доведётся поговорить об этом подробнее.
Байесовские рейтинг-системы
Ещё один пример, который лично мне близок – когда-то мы с Александром Сироткиным улучшили одну из байесовских рейтинг-систем; возможно, позднее в блоге мы поговорим о рейтинг-системах подробнее. Но здесь я просто приведу простейший пример – как работает рейтинг Эло для шахматистов? Если не вдаваться в аппроксимации и магические константы, суть очень простая: что такое вообще рейтинг? Мы хотели бы, чтобы рейтинг был мерилом силы игры; однако при этом совершенно очевидно, что сила игры от партии к партии может достаточно сильно меняться под воздействием внешних и внутренних случайных факторов. Таким образом, на самом деле сила игры того или иного участника в конкретной партии (сравнение этих сил и определяет исход партии) – это случайная величина, «истинная сила» игры шахматиста – её математическое ожидание, а рейтинг – это наша неточная оценка этого математического ожидания. Мы пока будем рассматривать простейший случай, в котором сила игры участника в конкретной партии нормально распределена вокруг его истинной силы с некоторой постоянной заранее фиксированной дисперсией (рейтинг Эло именно так и делает – отсюда и его магическая константа «шахматист с силой на 200 пунктов рейтинга больше набирает в среднем 0.75 очка за партию»). Перед каждой партией мы имеем некоторые априорные оценки силы игры каждого шахматиста; предположим, что априорное распределение тоже нормальное, с параметрами μ1, σ1 и μ2, σ2 соответственно. Наша задача – зная результат партии, пересчитать эти параметры. Картинка получается вот какая:
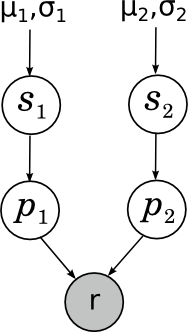
Здесь si (skill) – «истинная сила игры» шахматиста, pi (performance) – его сила игры, показанная в данной конкретной партии, а r – довольно интересно устроенная случайная переменная, показывающая результат партии, который получается из сравнения p1 и p2. Подробнее об этом сегодня не будем.
Поведение интернет-пользователей
И закончу ещё одним близким мне примером – моделями поведения интернет-пользователей в поисковых системах. Опять же, подробно вдаваться не буду – может быть, ещё вернёмся к этому, а пока можно почитать, например, нашу с Александром Фишковым обзорную статью – просто рассмотрю одну такую модель для примера. Мы пытаемся смоделировать, что делает пользователь, когда получает поисковую выдачу. Просмотр ссылки и клик трактуются как случайные события; для конкретной запросной сессии переменная Ei обозначает просмотр описания ссылки на документ, показанный на позиции i, Ci – клик на этой позиции. Введём упрощающее предположение: предположим, что процесс просмотра описаний всегда начинается с первой позиции и строго линеен. Позиция просматривается, только если все предыдущие позиции были просмотрены. В итоге наш виртуальный пользователь читает ссылки сверху вниз, если ему понравился (что зависит от релевантности ссылки), кликает, и, если документ действительно оказывается релевантным, пользователь уходит и больше не возвращается; любопытно, но факт: для поисковой системы хорошее событие – это когда пользователь как можно быстрее ушёл и не вернулся, а если он возвращается к выдаче, значит, не смог найти то, что искал.
В результате получается так называемая каскадная клик-модель (cascading click model, CCM); в ней пользователь следует вот такой блок-схеме:
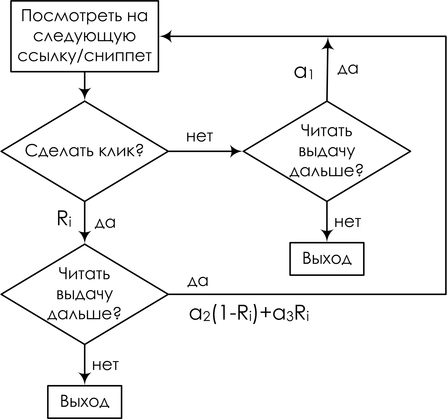
А в виде байесовской сети это можно нарисовать вот так:
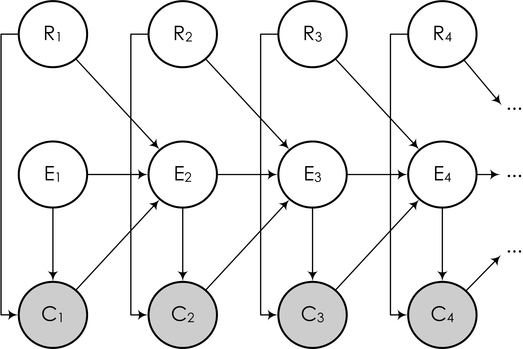
Здесь последующие события Ei (это событие «пользователь прочитал следующий сниппет», от слова examine) зависят от того, был ли клик на предыдущей ссылке, и если был, то оказалась ли ссылка действительно релевантной. Задача же снова описывается так же, как выше: мы наблюдаем часть переменных (клики пользователя), и должны на основании кликов обучить модель и сделать выводы о релевантности каждой ссылки (для того чтобы в дальнейшем переупорядочивать ссылки согласно их истинной релевантности), т.е. о значениях некоторых других переменных в модели.
Заключение и выводы
В этой статье мы рассмотрели несколько примеров вероятностных моделей, логика которых легко «считывается» из их направленных графических моделей. Кроме того, мы убедились: то, чего мы обычно хотим от вероятностной модели, можно представить в виде одной достаточно хорошо определённой задачи – в направленной графической модели пересчитать распределение одних переменных при известных значениях некоторых других переменных. Однако логика логикой, а как, собственно, обучать? Как решать эту задачу? Об этом – в следующих сериях.
 — вектор «степени выраженности» каждой темы в этом документе;
— вектор «степени выраженности» каждой темы в этом документе; по распределению
по распределению  ;
; с вероятностями, заданными в β.
с вероятностями, заданными в β.