 Доброго времени суток, читатель. Random Forest сегодня является одним из популярнейших и крайне эффективных методов решения задач машинного обучения, таких как классификация и регрессия. По эффективности он конкурирует с машинами опорных векторов, нейронными сетями и бустингом, хотя конечно не лишен своих недостатков. С виду алгоритм обучения крайне прост (в сравнении скажем с алгоритмом обучения машины опорных векторов, кому мало острых ощущений в жизни, крайне советую заняться этим на досуге). Мы же попробуем в доступной форме разобраться в основных идеях, заложенных в Random Forest (бинарное дерево решений, бутстреп аггрегирование или бэггинг, метод случайных подпространств и декорреляция) и понять почему все это вместе работает. Модель относительно своих конкурентов довольно таки молодая: началось все со статьи 1997 года в которой авторы предлагали способ построения одного дерева решений, используя метод случайных подпространств признаков при создании новых узлов дерева; затем был ряд статей, который завершился публикацией каноничной версии алгоритма в 2001 году, в котором строится ансамбль решающих деревьев на основе бутстреп агрегирования, или бэггинга. В конце будет приведен простой, совсем не шустрый, но крайне наглядный способ реализации этой модели на c#, а так же проведен ряд тестов. Кстати на фотке справа вы можете наблюдать настоящий случайный лес который произрастает у нас тут в Калининградской области на Куршской косе.
Доброго времени суток, читатель. Random Forest сегодня является одним из популярнейших и крайне эффективных методов решения задач машинного обучения, таких как классификация и регрессия. По эффективности он конкурирует с машинами опорных векторов, нейронными сетями и бустингом, хотя конечно не лишен своих недостатков. С виду алгоритм обучения крайне прост (в сравнении скажем с алгоритмом обучения машины опорных векторов, кому мало острых ощущений в жизни, крайне советую заняться этим на досуге). Мы же попробуем в доступной форме разобраться в основных идеях, заложенных в Random Forest (бинарное дерево решений, бутстреп аггрегирование или бэггинг, метод случайных подпространств и декорреляция) и понять почему все это вместе работает. Модель относительно своих конкурентов довольно таки молодая: началось все со статьи 1997 года в которой авторы предлагали способ построения одного дерева решений, используя метод случайных подпространств признаков при создании новых узлов дерева; затем был ряд статей, который завершился публикацией каноничной версии алгоритма в 2001 году, в котором строится ансамбль решающих деревьев на основе бутстреп агрегирования, или бэггинга. В конце будет приведен простой, совсем не шустрый, но крайне наглядный способ реализации этой модели на c#, а так же проведен ряд тестов. Кстати на фотке справа вы можете наблюдать настоящий случайный лес который произрастает у нас тут в Калининградской области на Куршской косе.Бинарное дерево решений
Начать следует с дерева, как с основного структурного элемента леса, но в контексте изучаемой модели. Изложение будет строится на предположении, что читатель понимает, что из себя представляет дерево, как структура данных. Построение дерева будет выполняться примерно по алгоритму CART (Classification and Regression Tree), который строит бинарные деревья решений. Кстати тут на хабре есть годная статья по построению таких деревьев на базе минимизации энтропии, в нашем варианте это будет частным случаем. Итак представьте себе пространство признаков, допустим двумерное, что бы было легче визуализировать, в котором задано множество объектов двух классов.

Введем ряд обозначений. Обозначим множество признаков следующим образом:
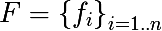
Для каждого признака можно выделить множество его значений, основываясь либо на обучающем множестве, либо используя другую априорную информацию о задаче, обозначим следующим образом конечное множество значений признака:
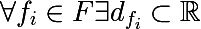
Так же необходимо ввести так называемую меру неоднородности множества относительно его меток. Представьте, что некоторое подмножество обучающего множества состоит из 5 красных и 10 синих объектов, тогда мы можем утверждать, что в этом подмножестве вероятность вытянуть красный объект будет 1/3, а синий 2/3. Обозначим следующим образом вероятность k-ого класса в некотором подмножестве обучающего множества:
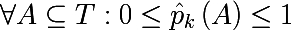
Таким образом мы задали эмпирическое дискретное вероятностное распределение меток в подмножестве наблюдений. Мерой неоднородности этого подмножества будем называть функцию следующего вида, где K(A) — общее количество меток подмножества A:
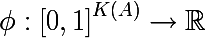
Мера неоднородности задается таким образом, что бы значение функции по возможности возрастало при увеличении разношерстности набора, достигая своего максимума тогда, когда набор состоит из одинакового количества всевозможных меток, и минимума в случае если набор состоит только из меток одного класса (еще раз советую взглянуть на энтропийный пример с картинками).
Давайте взглянем на некоторые примеры мер неоднородности (вектор p состоит из m вероятностей меток встречающихся в некотором подмножестве A обучающего множества):
- Most commonly occurring class:
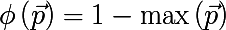
- Gini index:
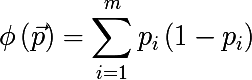
- Cross-entropy:
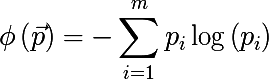
Алгоритм построения бинарного дерева решений работает по схеме жадного алгоритма: на каждой итерации для входного подмножества обучающего множества строится такое разбиение пространства гиперплоскостью (ортогональной одной их осей координат), которое минимизировало бы среднюю меру неоднородности двух полученных подмножеств. Данная процедура выполняется рекурсивно для каждого полученного подмножества до тех пор, пока не будут достигнуты критерии остановки. Запишем это более формально, для входного множества A найдем пару <признак, значение признака>, что мера неоднородности будет минимальна:
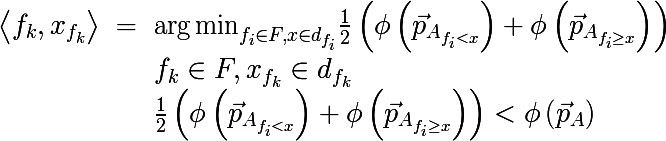
где
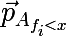 — вектор вероятностей полученный по вышеописанной процедуре от подмножества множества A, состоящего из тех элементов для которых выполняется условие f < x. Так же не стоит забывать, что средняя стоимость разбиения не должна превышать стоимость исходного множества. Давайте теперь вернемся к исходной картинке и глянем что реально происходит, разделим вышеописанным образом исходное множество данных:
— вектор вероятностей полученный по вышеописанной процедуре от подмножества множества A, состоящего из тех элементов для которых выполняется условие f < x. Так же не стоит забывать, что средняя стоимость разбиения не должна превышать стоимость исходного множества. Давайте теперь вернемся к исходной картинке и глянем что реально происходит, разделим вышеописанным образом исходное множество данных: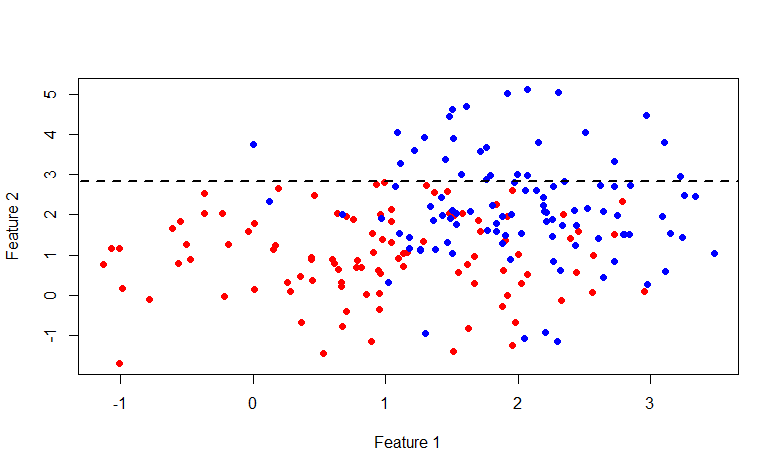
Как видите множество выше линии y=2.840789 полностью состоит из синих меток, таким образом имеет смыл разбивать далее только второе множество.
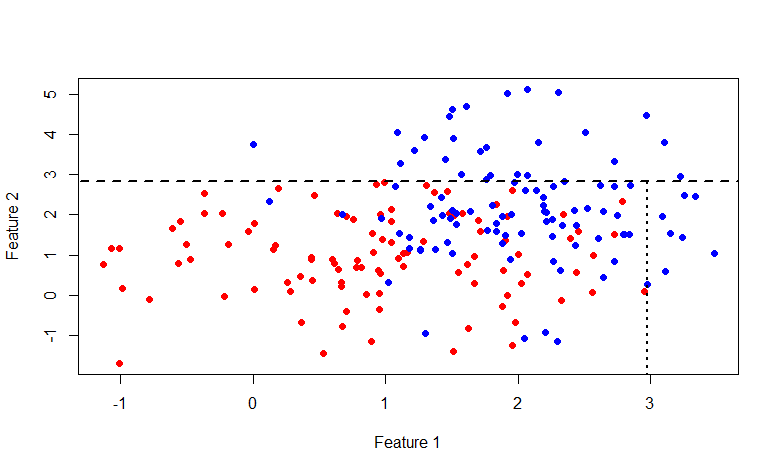
В этот раз линия x=2.976719. В общем кому интересно побаловаться с этой картинкой, вот код на R:
Код визуализации
rm(list=ls())
library(mvtnorm)
labCount <- 100
lab1 <- rmvnorm(n=labCount, mean=c(1,1), sigma=diag(c(1, 1)))
lab0 <- rmvnorm(n=labCount, mean=c(2,2), sigma=diag(c(0.5, 2)))
df <- data.frame(x=append(lab1[, 1], lab0[, 1]),
y=append(lab1[, 2], lab0[, 2]),
lab=append(rep(1, labCount), rep(0, labCount)))
plot(df$x, df$y, col=append(rep("red", labCount), rep("blue", labCount)), pch=19,
xlab="Feature 1", ylab="Feature 2")
giniIdx <- function(data)
{
p1 <- sum(data$lab == 1)/length(data$lab)
p0 <- sum(data$lab == 0)/length(data$lab)
return(p0*(1 - p0) + p1*(1 - p1))
}
p.norm <- giniIdx
getSeparator <- function(data)
{
idx <- NA
idx.val <- NA
cost <- p.norm(data)
for(i in 1:(dim(data)[2] - 1))
{
for(i.val in unique(data[, i]))
{
#print(paste("i = ", i, "; v = ", i.val, sep=""))
cost.tmp <- 0.5*(p.norm(data[data[, i] < i.val, ]) +
p.norm(data[data[, i] >= i.val, ]))
if(is.nan(cost.tmp))
{
next
}
if(cost.tmp < cost)
{
cost <- cost.tmp
idx <- i
idx.val <- i.val
}
}
}
return(c(idx, idx.val))
}
s1 <- getSeparator(df)
lines(c(-100, 100), c(s1[2], s1[2]), lty=2, lwd=2, type="l")
Перечислим возможные критерии остановки: достигнута максимальная глубина узла; вероятность доминирующего класса в разбиении превышает некоторый порог (я использую 0.95); количество элементов в подмножестве меньше некоторого порога. В итоге у нас получится разбиение всего множества на (гипер)прямоугольники, и каждое такое подмножество множества обучения будет ассоциировано с одним листом дерева, а все внутренние узлы представляют из себя одно из условий разбиения; или другими словами некоторый предикат. У текущего узла, левый потомок ассоциирован с теми элементами множества, для которых предикат верен, а правый соответственно с тему для которых предикат возвращает ложь. Выглядит это примерно следующим образом:

Итак мы получили дерево, как же принять на нем решение? Нам не составит труда определить к какому из подмножеств обучающего множества принадлежит любой входной образ, по мнению конкретного дерева решений. Далее нам остается только выбрать доминирующий класс в данном подмножестве и вернуть его клиенту, либо вернуть вероятностное распределение меток в данном подмножестве.
Кстати на счет задачи регрессии. Описанный способ построения дерева легко меняется с задачи классификации на задачу регрессии. Для этого необходимо заменить меру неоднородности на некоторую меру ошибки прогнозирования, например на среднеквадратичное отклонение. А при принятии решения вместо доминирующего класса используется среднее значение целевой переменной.
Вроде с деревьями все порешали. Мы не будем останавливаться на плюсах и минусах этого метода, в википедии есть хороший список. Но в конце хочется добавить иллюстрацию из книги An Introduction to Statistical Learning про разницу линейных моделей и деревьев.
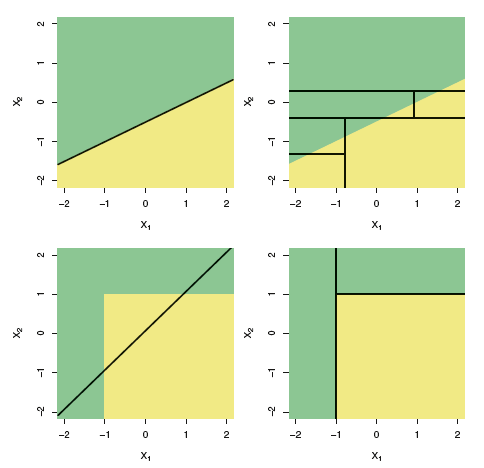
Данная иллюстрация показывает разницу между линейной моделью и бинарным деревом решений, как видите в случае линейной разделимости, в общем дерево будет показывать менее точный результат нежели простой линейный классификатор.
Bootstrap aggregating или bagging
Перейдем к следующей идейной составляющей random forest'а. Итак название BAGging, образовано от Bootstrap AGgregating. В статистике под бутстрепом понимают как способ оценки стандартной ошибки статистик выборочного вероятностного распределения, так и способ семплирования выборок из набора данных основанный на методе Монте-Карло.
Бутстреп семплинг довольно таки прост по своей идее, и применяется тогда, когда мы не имеем возможности получить большое количество выборок из реального распределения, а это почти всегда так. Допустим мы хотим получить m множеств наблюдений размера n, но у нас в распоряжении только одно множество из n наблюдений. Тогда мы генерируем m множеств равновероятностым выбором n элементов из исходного множества с возвратом выбранного элемента (выборка с повторением или возвращением). При больших значениях n, количество уникальных элементов полученного бутстреп семплингом множества будет составлять (1 — 1/e) ≈ 63.2% от общего числа уникальных наблюдений исходного множества. Обозначим Di — i-ое множество полученное бутстреп семплированием, мы оцениваем на нем некоторый параметр ai, и повторяем эту процедуру m раз. Стандартная ошибка бутстреп оценки параметра записывается следующим образом:
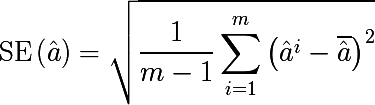
Итак, статистический бутстреп позволяет оценить ошибку оценки некоторого параметра распределения. Но это так отвлечение от темы, нам же интересен метод бутстреп семплирования.
А теперь рассмотрим набор из m независимых случайно выбранных элементов x из одного вероятностного распределения, с некоторым математическим ожиданием и дисперсией σ2. Тогда выборочное среднее будет равно:
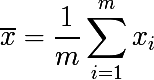
Выборочное среднее — это не параметр распределения, в отличие от матожидания и дисперсии, а функция от случайных переменных, т.е. тоже является случайной переменной, из некоторого вероятностного распределения выборочных средних. А оно в свою очередь обладает параметром дисперсия, который выражается следующим образом:
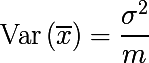
Получается, что усреднение множества значений случайной переменной уменьшает вариативность. На этом и строится идея агрегирования бутстреп выборок. Сгенерируем m бутстреп выборок размера n из обучающего множества D (тоже размера n):
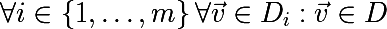
На каждой бутстреп выборке обучим модель f и введем следующую функцию, такой подход и называется bootstrap aggregating или bagging:
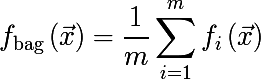
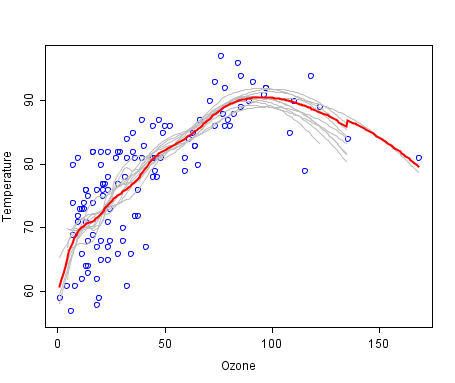
Bagging можно проиллюстрировать следующим графиком из википедии, где bag-модель изображена красной линией и является усреднением множества других моделей.
Декорреляция
Думаю уже понятно как получить просто лес: сгенерируем некоторое количество бутстреп выборок и обучим дерево решений на каждой из них. Но тут существует небольшая проблема, почти все деревья будут более или менее одинаковой структуры. Давайте проведем эксперимент, возьмем множество с двумя классами и 32-мя фичами, построим 1000 деревьев решений на бутстреп семплах, и посмотрим на вариативность предиката корневого узла.
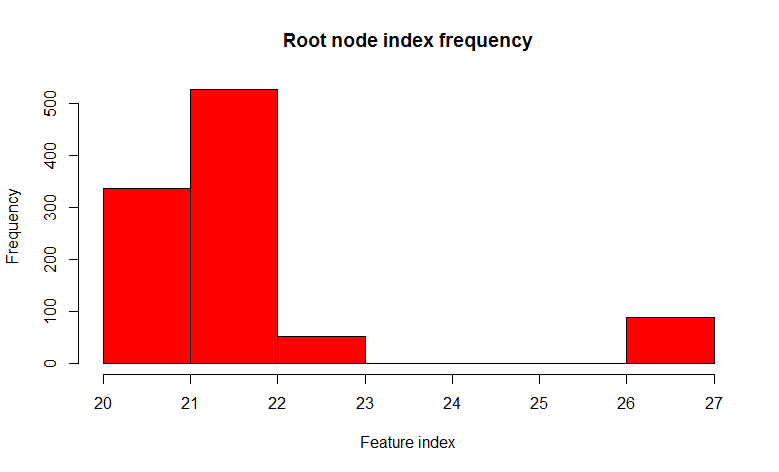
Мы видим что из 1000 деревьев 22-ой признак (очевидно значение фичи одно и тоже) встречается в 526 деревьях, и почти во всех дочерние ноды одинаковые. Другими словами деревья скоррелированны относительно друг друга. Получается, что нет смысла строить 1000 деревьев, если достаточно всего нескольких, а чаще всего одного или двух. А теперь давайте попробуем при построении дерева использовать при разделении каждого узла только некоторый небольшой случайный набор признаков из множества всех признаков, скажем 7 случайных из 32.
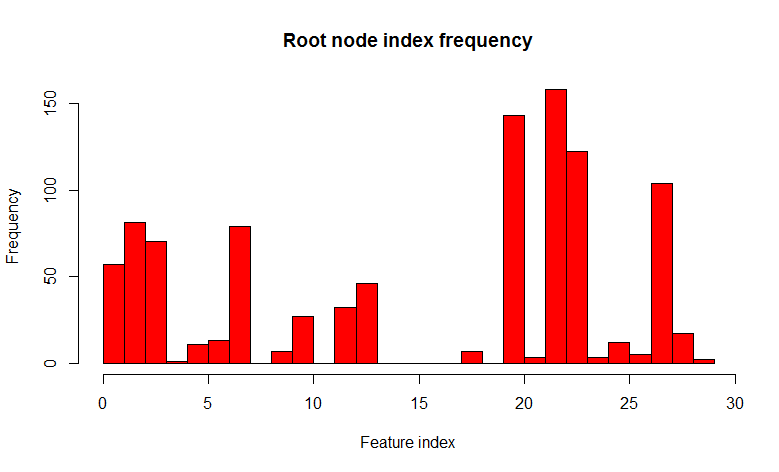
Как видите, распределение значительно изменилось в сторону большего разнообразия деревьев (кстати не только в корневом узле, но и в дочерних), что и было целью такого трюка. Теперь 22 признак встречается только в 158 случаях. Выбор "7 случайных из 32 признаков" обоснован эмпирическим наблюдением (я так и не нашел автора этого наблюдения), и в задачах классификации это как правило квадратный корень из общего количества признаков. Другими словами деревья стали менее скореллированными, а процесс называется декорреляция.
Такой метод, в общем, называется Random subspace method и применяется не только для деревьев решений, но и для других моделей, таких как нейросети.
В общем как то так выглядел бы обычный ровный лес, и декоррелированный.

Код
Перейдем к реализации. Еще раз хочу напомнить, что приведенный мной пример не является быстрой реализацией random forest'а, а носит учебный лишь характер, призванной помочь понять основные идеи модели. Например тут вы найдете пример годной и шустрой имплементации, но к сожалению менее понятной.
Комментарии я буду вставлять там где необходимо прямо в коде, что бы не разбивать классы на куски.
Обычное дерево
// обычное темплейт дерево, хотя конечно для бинарного дерева можно было бы сделать и проще
public class TreeNode<T>
{
public TreeNode()
{
Childs = new LinkedList<TreeNode<T>>();
}
public TreeNode(T data)
{
Data = data;
Childs = new LinkedList<TreeNode<T>>();
}
public TreeNode<T> Parent { get; set; }
public LinkedList<TreeNode<T>> Childs { get; set; }
public T Data { get; set; }
public virtual bool AddChild(T data)
{
TreeNode<T> node = new TreeNode<T>() {Data = data};
node.Parent = this;
Childs.AddLast(node);
return true;
}
public virtual bool AddChild(TreeNode<T> node)
{
node.Parent = this;
Childs.AddLast(node);
return true;
}
public bool IsLeaf
{
get
{
return Childs.Count == 0;
}
}
public int Depth
{
get
{
int d = 0;
TreeNode<T> node = this;
while (node.Parent != null)
{
d++;
node = node.Parent;
}
return d;
}
}
}
Единица наблюдения в моем случае представляется следующим классом.
Observation
public class DataItem<T>
{
private T[] _input = null;
private T[] _output = null;
public DataItem()
{
}
public DataItem(T[] input, T[] output)
{
_input = input;
_output = output;
}
public T[] Input
{
get { return _input; }
set { _input = value; }
}
public T[] Output
{
get { return _output; }
set { _output = value; }
}
}
Для каждого узла дерева необходимо хранить информацию о предикате, который используется для принятия решения о классификации.
Данные узла дерева
public class ClassificationTreeNodeData
{
// вектор вероятностей <id класса, его вероятность>, будем считать что он отсортирован по убыванию вероятностей
// это то самое p из вышеприведенных формул первого раздела
internal IDictionary<double, double> Probabilities { get; set; }
// стоимость данного узла, используется для того, что бы разбиение не было дороже текущей стоимости
// чуть ниже мы представим это как норму вектора
internal double Cost { get; set; }
// предикат который будет использоваться для принятия решения, полностью излишний элемент,
// добавлен только ради эстетики, ведь мы не преследуем цель написать очень быстрый и экономный вариант -)
internal Predicate<double[]> Predicate { get; set; }
// данные ассоциированные с текущей нодой, используется только во время обучения дерева
internal IList<DataItem<double>> DataSet { get; set; }
// имя ноды, используется при визуализации дерева
internal string Name { get; set; }
// индекс признака который минимизирует стоимость при разбиении
internal int FeatureIndex { get; set; }
// значение порога из области определения признака
internal double FeatureValue { get; set; }
// следующие две функции нужны изза того что дотнет не хочет сериализовать замыкания, которым является предикат
[OnSerializing]
private void OnSerializing(StreamingContext context)
{
Predicate = null;
}
[OnDeserialized]
[OnSerialized]
private void OnDeserialized(StreamingContext context)
{
Predicate = v => v[FeatureIndex] < FeatureValue;
}
}
Рассмотрим класс бинарного решающего дерева.
Бинарное решающее дерево
public class ClassificationBinaryTree
{
private TreeNode<ClassificationTreeNodeData> _rootNode = null;
private INorm<double> _norm = null; // норма вектора вероятностей
private int _minLeafDataCount = 1; // минимально количество данных в наборе данных терминальной ноды
private int[] _trainingFeaturesSubset = null; // подмножество фичь которые могут участвовать в сплиттинге узла
private int _randomSubsetSize = 0; // размер случайновыбираемых фич, как кандидатов при разделении ноды
private Random _random = null;
private double _maxProbability = 0; // максимальная вероятность класса, после достижения которой разделение ноды не происходит
private int _maxDepth = Int32.MaxValue; // максимальная глубина ноды
private bool _showLog = false;
private int _featuresCount = 0;
public ClassificationBinaryTree(INorm<double> norm, int minLeafDataCount, int[] trainingFeaturesSubset = null,
int randomSubsetSize = 0, double maxProbability = 0.95, int maxDepth = Int32.MaxValue,
bool showLog = false)
{
_norm = norm;
_minLeafDataCount = minLeafDataCount;
_trainingFeaturesSubset = trainingFeaturesSubset;
_randomSubsetSize = randomSubsetSize;
_maxProbability = maxProbability;
_maxDepth = maxDepth;
_showLog = showLog;
}
public TreeNode<ClassificationTreeNodeData> RootNode
{
get
{
return _rootNode;
}
}
// обучение дерева
public void Train(IList<DataItem<double>> data)
{
_featuresCount = data.First().Input.Length;
if (_randomSubsetSize > 0)
{
_random = new Random(Helper.GetSeed());
}
IDictionary<double, double> rootProbs = ComputeLabelsProbabilities(data);
_rootNode = new TreeNode<ClassificationTreeNodeData>(new ClassificationTreeNodeData()
{
DataSet = data,
Probabilities = rootProbs,
Cost = _norm.Calculate(rootProbs.Select(x => x.Value).ToArray())
});
// не люблю рекурсии
Queue<TreeNode<ClassificationTreeNodeData>> queue = new Queue<TreeNode<ClassificationTreeNodeData>>();
queue.Enqueue(_rootNode);
while (queue.Count > 0)
{
if (_showLog)
{
Logger.Instance.Log("Tree training: queue size is " + queue.Count);
}
TreeNode<ClassificationTreeNodeData> node = queue.Dequeue();
int sourceCount = node.Data.DataSet.Count;
// разделение ноды
TrainNode(node, node.Data.DataSet, _trainingFeaturesSubset, _randomSubsetSize);
if (_showLog && node.Childs.Count() > 0)
{
Logger.Instance.Log("Tree training: source " + sourceCount + " is splitted into " +
node.Childs.First().Data.DataSet.Count + " and " +
node.Childs.Last().Data.DataSet.Count);
}
// проверка остановки и продолжение роста дерева
foreach (TreeNode<ClassificationTreeNodeData> child in node.Childs)
{
if (child.Data.Probabilities.Count == 1 ||
child.Data.DataSet.Count <= _minLeafDataCount ||
child.Data.Probabilities.First().Value > _maxProbability ||
child.Depth >= _maxDepth)
{
child.Data.DataSet = null;
continue;
}
queue.Enqueue(child);
}
}
}
// разделение ноды
private void TrainNode(TreeNode<ClassificationTreeNodeData> node, IList<DataItem<double>> data, int[] featuresSubset, int randomSubsetSize)
{
// argmin нормы
double minCost = node.Data.Cost;
int idx = -1;
double threshold = 0;
IDictionary<double, double> minLeftProbs = null;
IDictionary<double, double> minRightProbs = null;
IList<DataItem<double>> minLeft = null;
IList<DataItem<double>> minRight = null;
double minLeftCost = 0;
double minRightCost = 0;
// если требуется случайное подмножество фич, то заполняе
if (randomSubsetSize > 0)
{
featuresSubset = new int[randomSubsetSize];
IList<int> candidates = new List<int>();
for (int i = 0; i < _featuresCount; i++)
{
candidates.Add(i);
}
for (int i = 0; i < randomSubsetSize; i++)
{
int idxRandom = _random.Next(0, candidates.Count);
featuresSubset[i] = candidates[idxRandom];
candidates.RemoveAt(idxRandom);
}
}
else if (featuresSubset == null)
{
featuresSubset = new int[data.First().Input.Length];
for (int i = 0; i < data.First().Input.Length; i++)
{
featuresSubset[i] = i;
}
}
// пробегаемся по выбранным признакам
foreach (int i in featuresSubset)
{
IList<double> domain = data.Select(x => x.Input[i]).Distinct().ToList();
// и ищем порог для минимизации стоимости разбиения
foreach (double t in domain)
{
IList<DataItem<double>> left = new List<DataItem<double>>(); // подмножество обучающего множества левого потомка
IList<DataItem<double>> right = new List<DataItem<double>>(); // ну и правого
IDictionary<double, double> leftProbs = new Dictionary<double, double>(); // вектор вероятностей классов в подмножестве
IDictionary<double, double> rightProbs = new Dictionary<double, double>();
foreach (DataItem<double> di in data)
{
if (di.Input[i] < t)
{
left.Add(di);
if (!leftProbs.ContainsKey(di.Output[0]))
{
leftProbs.Add(di.Output[0], 0);
}
leftProbs[di.Output[0]]++;
}
else
{
right.Add(di);
if (!rightProbs.ContainsKey(di.Output[0]))
{
rightProbs.Add(di.Output[0], 0);
}
rightProbs[di.Output[0]]++;
}
}
if (right.Count == 0 || left.Count == 0)
{
continue;
}
// нормализация вероятностей
leftProbs = leftProbs.ToDictionary(x => x.Key, x => x.Value/left.Count);
rightProbs = rightProbs.ToDictionary(x => x.Key, x => x.Value/right.Count);
double leftCost = _norm.Calculate(leftProbs.Select(x => x.Value).ToArray()); // вычисление стоимости разбиения
double rightCost = _norm.Calculate(rightProbs.Select(x => x.Value).ToArray());
double avgCost = (leftCost + rightCost)/2; // средняя стоимость разбиения
if (avgCost < minCost)
{
minCost = avgCost;
idx = i;
threshold = t;
minLeftProbs = leftProbs;
minRightProbs = rightProbs;
minLeft = left;
minRight = right;
minLeftCost = leftCost;
minRightCost = rightCost;
}
}
}
// заполняем данные для текущей ноды и создаем потомков
node.Data.DataSet = null;
if (idx != -1)
{
//node should be splitted
node.Data.Predicate = v => v[idx] < threshold; // предикат который будет использоваться при принятии решений
node.Data.Name = "x[" + idx + "] < " + threshold;
node.Data.Probabilities = null;
node.Data.FeatureIndex = idx;
node.Data.FeatureValue = threshold;
node.AddChild(new ClassificationTreeNodeData()
{
Probabilities = minLeftProbs.OrderByDescending(x => x.Value).ToDictionary(x => x.Key, x => x.Value),
DataSet = minLeft,
Cost = minLeftCost
});
node.AddChild(new ClassificationTreeNodeData()
{
Probabilities = minRightProbs.OrderByDescending(x => x.Value).ToDictionary(x => x.Key, x => x.Value),
DataSet = minRight,
Cost = minRightCost
});
}
}
// вычисление вероятностей классов в множестве, применяется в режиме классификации
private IDictionary<double, double> ComputeLabelsProbabilities(IList<DataItem<double>> data)
{
IDictionary<double, double> p = new Dictionary<double, double>();
double denominator = data.Count;
foreach (double label in data.Select(x => x.Output[0]).Distinct())
{
p.Add(label, data.Where(x => x.Output[0] == label).Count() / denominator);
}
return p;
}
// классификация вхожного образа
public IDictionary<double, double> Classify(double[] v)
{
TreeNode<ClassificationTreeNodeData> node = _rootNode;
while (!node.IsLeaf)
{
node = node.Data.Predicate(v) ? node.Childs.First() : node.Childs.Last();
}
return node.Data.Probabilities;
}
// запись дерева в формате GraphVis http://www.graphviz.org/
public void WriteDotFile(StreamWriter sw, bool separateTerminalNode = false)
{
sw.WriteLine("digraph G{");
sw.WriteLine("graph [ordering=\"out\"];");
Queue<TreeNode<ClassificationTreeNodeData>> q = new Queue<TreeNode<ClassificationTreeNodeData>>();
q.Enqueue(_rootNode);
int terminalCount = 0;
ISet<string> styles = new HashSet<string>();
while (q.Count > 0)
{
TreeNode<ClassificationTreeNodeData> node = q.Dequeue();
foreach (TreeNode<ClassificationTreeNodeData> child in node.Childs)
{
string childName = child.Data.Name;
if (String.IsNullOrEmpty(childName))
{
if (separateTerminalNode)
{
childName = "TNode #" + terminalCount + "; Class: " + child.Data.Probabilities.First().Key;
}
else
{
childName = "Class: " + child.Data.Probabilities.First().Key;
}
styles.Add("\"" + childName + "\" [" +
"color=red, style=filled" +
"];");
terminalCount++;
}
sw.WriteLine("\"" + node.Data.Name + "\" -> " + "\"" + childName + "\";");
q.Enqueue(child);
}
}
foreach (string style in styles)
{
sw.WriteLine(style);
}
sw.WriteLine("}");
}
}
Остановимся на норме, используемой в классе решающего дерева.
Интерфейс нормы
public interface INorm<T>
{
double Calculate(T[] v);
}
Индекс Gini
internal class GiniIndex : INorm<double>
{
#region INorm<double> Members
public double Calculate(double[] v)
{
return v.Sum(p => p*(1 - p));
}
#endregion
}
Перекрестная энтропия
internal class MetricsBasedNorm<T> : INorm<T>
{
private IMetrics<T> _m = null;
internal MetricsBasedNorm(IMetrics<T> m)
{
_m = m;
}
#region INorm<T> Members
public double Calculate(T[] v)
{
return _m.Calculate(v, v);
}
#endregion
}
public interface IMetrics<T>
{
/// <summary>
/// Calculate value of metrics
/// </summary>
double Calculate(T[] v1, T[] v2);
/// <summary>
/// Get centroid/clusteroid of data
/// </summary>
T[] GetCentroid(IList<T[]> data);
/// <summary>
/// Calculate value of partial derivative by v2[v2Index]
/// </summary>
T CalculatePartialDerivaitveByV2Index(T[] v1, T[] v2, int v2Index);
}
internal class CrossEntropy : MetricsBase<double>
{
internal CrossEntropy()
{
}
/// <summary>
/// \sum_i v1_i * ln(v2_i)
/// </summary>
public override double Calculate(double[] v1, double[] v2)
{
if (v1.Length != v2.Length)
{
throw new ArgumentException("Length of v1 and v2 should be equal");
}
if (v1.Length == 0 || v2.Length == 0)
{
throw new ArgumentException("Vector dimension can't be 0");
}
double d = 0;
for (int i = 0; i < v1.Length; i++)
{
d += v1[i]*Math.Log(v2[i] + Double.Epsilon);
}
return -d;
}
public override double CalculatePartialDerivaitveByV2Index(double[] v1, double[] v2, int v2Index)
{
return v2[v2Index] - v1[v2Index];
}
}
Ну и осталось рассмотреть только сам класс random forest.
Random Forest
public class ClassificationRandomForest
{
// параметры почти те же самые, добавился один
private INorm<double> _norm = null;
private int _minLeafDataCount = 1;
private int[] _trainingFeaturesSubset = null;
private int _randomSubsetSize = 0; //zero if all features needed
private double _maxProbability = 0;
private int _maxDepth = Int32.MaxValue;
private bool _showLog = false;
private int _forestSize = 0; // размер леса
private ConcurrentBag<ClassificationBinaryTree> _trees = null;
public ClassificationRandomForest(INorm<double> norm, int forestSize, int minLeafDataCount, int[] trainingFeaturesSubset = null,
int randomSubsetSize = 0, double maxProbability = 0.95, int maxDepth = Int32.MaxValue,
bool showLog = false)
{
_norm = norm;
_minLeafDataCount = minLeafDataCount;
_trainingFeaturesSubset = trainingFeaturesSubset;
_randomSubsetSize = randomSubsetSize;
_maxProbability = maxProbability;
_maxDepth = maxDepth;
_forestSize = forestSize;
_showLog = showLog;
}
public void Train(IList<DataItem<double>> data)
{
if (_showLog)
{
Logger.Instance.Log("Training is started");
}
// грех не распараллелить такое обучение, что бы каждое дерево росло самостоятельно
_trees = new ConcurrentBag<ClassificationBinaryTree>();
Parallel.For(0, _forestSize, i =>
{
ClassificationBinaryTree ct = new ClassificationBinaryTree(
_norm,
_minLeafDataCount,
_trainingFeaturesSubset,
_randomSubsetSize,
_maxProbability,
_maxDepth,
false
);
ct.Train(BasicStatFunctions.Sample(data, data.Count, true));
_trees.Add(ct);
if (_showLog)
{
Logger.Instance.Log("Training of tree #" + _trees.Count + " is completed!");
}
});
}
// классификация, по сути это и есть bagging
public IDictionary<double, double> Classify(double[] v)
{
IDictionary<double, double> p = new Dictionary<double, double>();
foreach (ClassificationBinaryTree ct in _trees)
{
IDictionary<double, double> tr = ct.Classify(v);
double winClass = tr.First().Key;
if (!p.ContainsKey(winClass))
{
p.Add(winClass, 0);
}
p[winClass]++;
}
double denominator = p.Sum(x => x.Value);
return
p.ToDictionary(x => x.Key, x => x.Value/denominator)
.OrderByDescending(x => x.Value)
.ToDictionary(x => x.Key, x => x.Value);
}
public IList<ClassificationBinaryTree> Forest
{
get
{
return _trees.ToList();
}
}
}
Заключение и ссылки
Если вы смотрели в код, то могли заметить, что в дереве есть функция для записи структуры и условий в dot формат, который визуализируется программой GraphVis. Если запустить случайный лес со следующими параметрами на вышеупомянутом множестве:
ClassificationRandomForest crf = new ClassificationRandomForest(
NormCreator.CreateByMetrics(MetricsCreator.CrossEntropy()),
10,
1,
null,
Convert.ToInt32(Math.Round(Math.Sqrt(ds.TrainSet.First().Input.Length))),
0.95,
1000,
true
);
crf.Train(ds.TrainSet);
То следующий код поможет нам визуализировать этот лес:
foreach (ClassificationBinaryTree tree in crf.Forest)
{
using (StreamWriter sw = new StreamWriter(@"e:\Neuroximator\NetworkTrainingOCR\TreeTestData\Forest\" +
(new DirectoryInfo(@"e:\Neuroximator\NetworkTrainingOCR\TreeTestData\Forest\")).GetFiles().Count()
+ ".dot"))
{
tree.WriteDotFile(sw);
sw.Close();
}
}
dot.exe -Tpng "tree.dot" -o "tree.png"
Давайте глянем на некоторые из них, они получаются совсем разные благодаря декорреляции.
Раз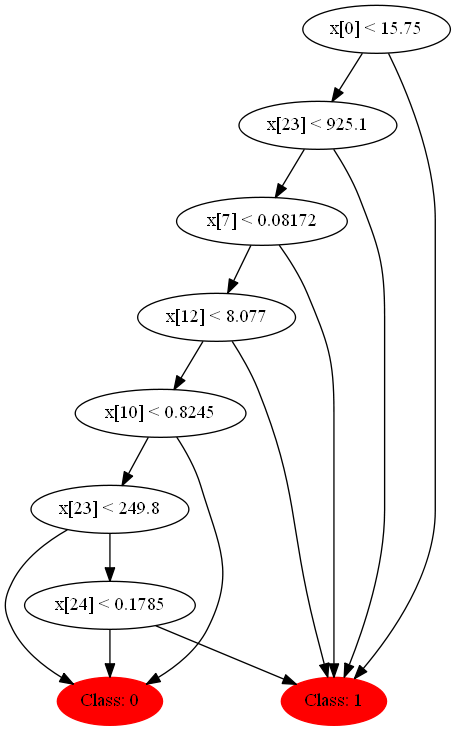

Два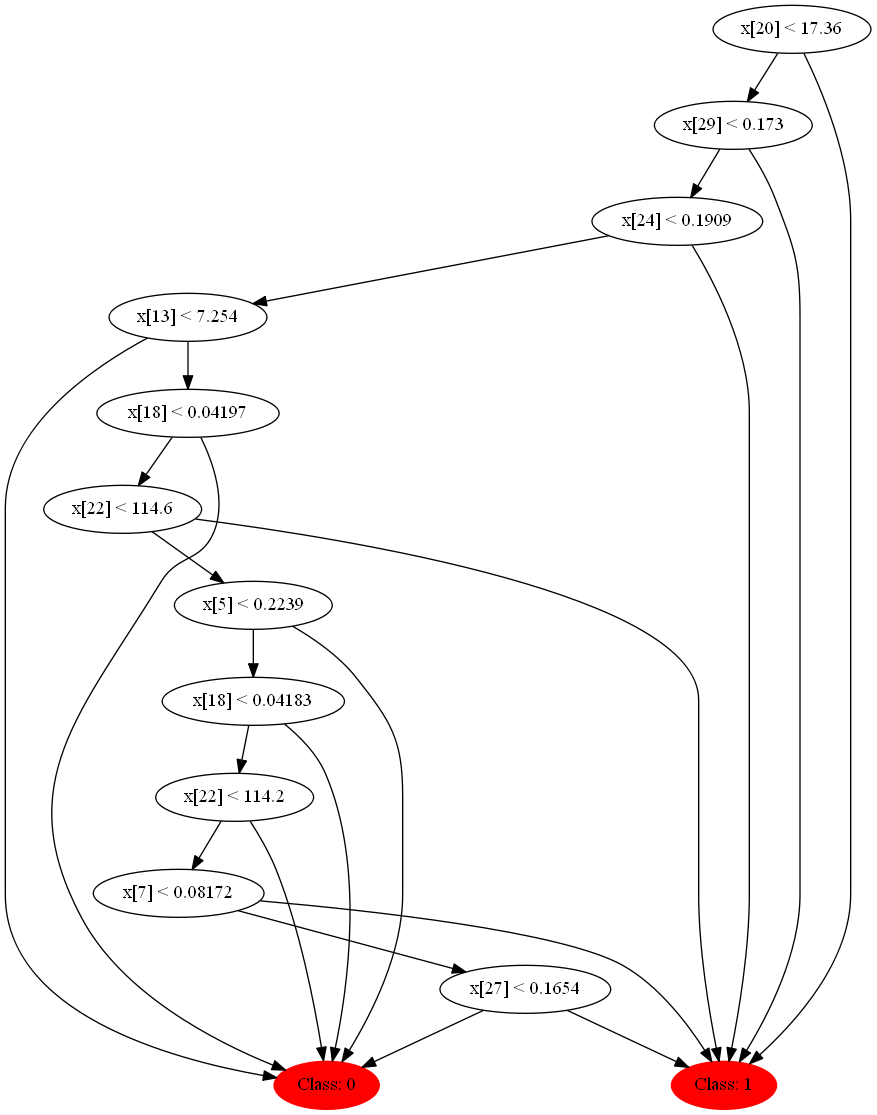

Три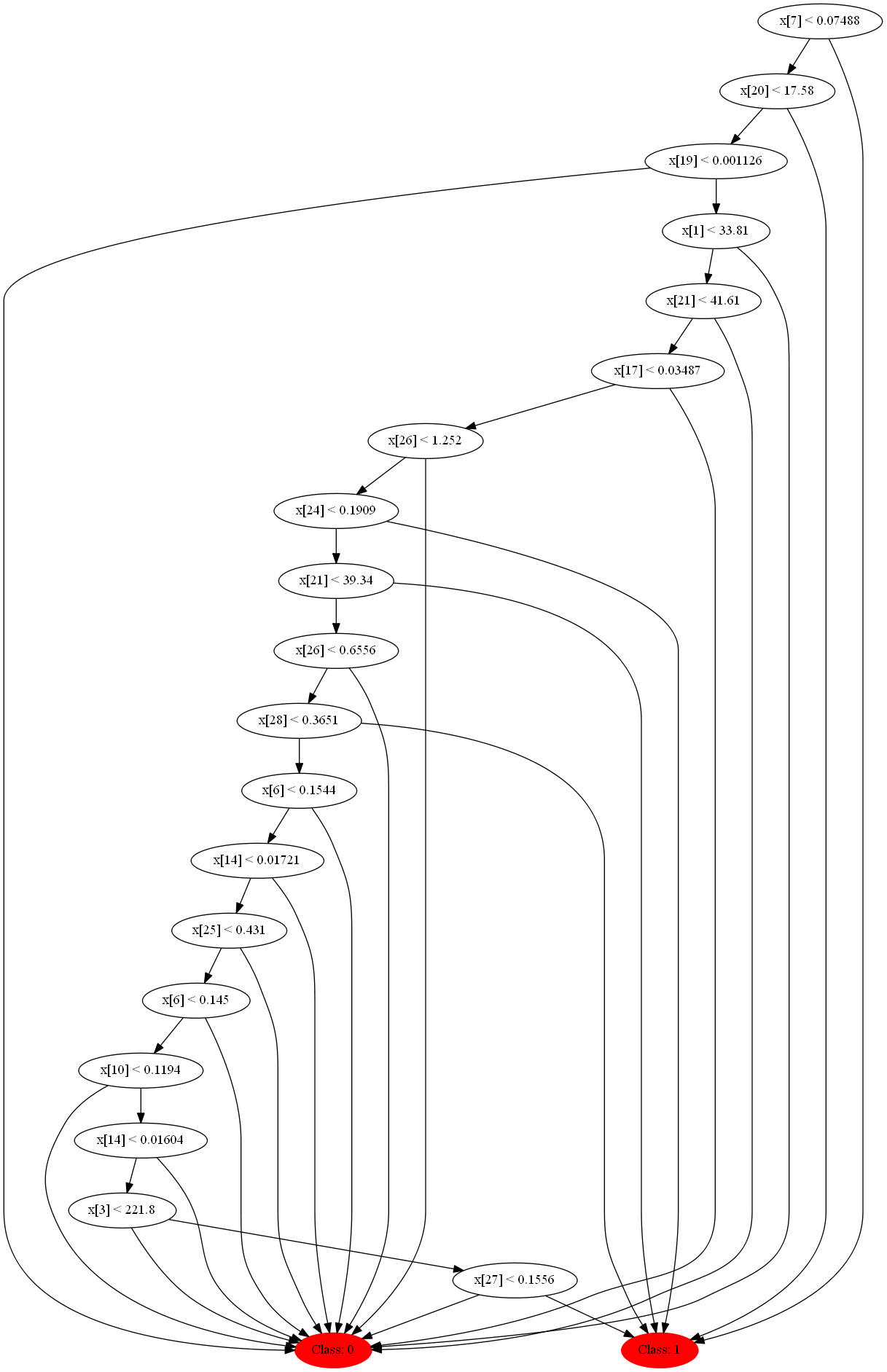

Ну и напоследок несколько полезных ссылок: