В комментариях к моей предыдущей статье о происходящем в нейронной сети проскользнула фраза, что, к сожалению, визуализация процессов обучения редко бывает возможна на реальных задачах с большими данными. Действительно очень жаль. Давайте же попытаемся это исправить. Под катом я предлагаю простую и, как ни удивительно, информативную визуализацию процесса обучения нейронной сети, не зависящую ни от характера задачи, ни от свойств самой сети, то есть доступную для сколь угодно сложной задачи.
Подготовка
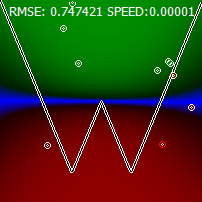
Задача для решения сетью взята из прошлой статьи. Нейронной сети на вход подаётся два числа – две координаты, и предлагается определить, находится ли эта точка выше графика. На выходе ожидается -1, +1 или 0 (если точка точно лежит на графике). На этот раз задача будет симметризована. Координаты берутся из диапазона [-0.5; +0.5], точка 0.0 будет точно в центре картинки и график также проходит через неё, так что ожидаемое значение в этой точке также 0. Площадь над графиком и площадь под графиком равны. Так что в среднем на каждом входе у нас 0, и на выходе в среднем ожидается также 0.
Мы возьмём сеть, состоящую из 3 слоёв по 15 нейронов в каждом (функция активации – гипертангенс) и будем обучать её с помощью классического метода обратного распространения и стохастического градиентного спуска с постепенно замедляющейся скоростью. Мы будем смотреть, чему научилась сеть, как это изображено на картинке выше. Сети будут предлагаться все точки диапазона, и в зависимости от данного ответа точка будет окрашиваться в разные оттенки зелёного(если ответ сети больше 0), оттенки красного (если значение меньше 0) и наконец, оттенками синего (если ответ даваемый сетью – 0 или его окрестности). На картинке выше представлены результаты полностью обученной сети, у которой среднеквадратическая ошибка 0.22, если смотреть только на знак правильных ответов будет сильно больше 99%
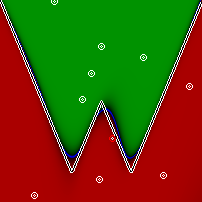
Замечу, кстати, что совсем обыкновенная нейронная сеть попросту не справляется с этой, казалось бы, несложной задачкой. Получается всегда что-то на вроде этого:
Чтобы решить эту проблему мы, как предлагалось в прошлой статье, сделаем сети три входа и на третий подадим константу 1. После этого задача становится для сети посильной.
Весь код для проверки и самостоятельных экспериментов можно посмотреть в предыдущей статье.
Визуализация
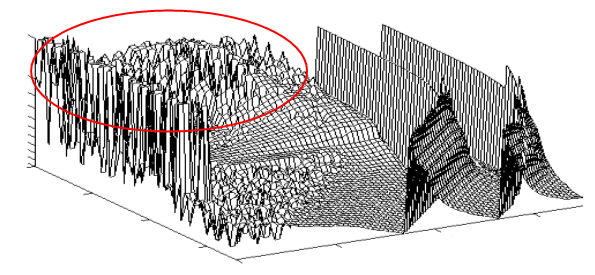
Теперь главная идея визуализации. Итак, у нас есть сеть, в которой в общей сложности 510 синапсов. Процесс обучения этой сети представляет собой изменение весов этих синапсов. Это можно представить как блуждание по 510-мерному пространству. И в каждой точке этого пространства у сети есть та или иная эффективность. Эта эффективность образует рельеф. Примерно как на картине, только не 2-мерная картинка, а 510-мерная. Пока трудно представить, согласен. Но это рельеф, а значит сеть, путешествующая по этому рельефу, будет вести себя примерно так же как мы, когда ищем дорогу наощупь. Мозг человека приспособлен решать такие задачи, а значит, поведение сети, возможно, будет нам интуитивно понятно.
Бывают участки, где рельеф гладкий, но в основном он сильно изрезан, как на обведённом кружком участке. Однако даже если рельеф очень зубастый и состоит из большого количества локальных максимумов, у него может быть достаточно гладкая огибающая.
Алгоритм обучения, получая толчки от отдельных обучающих примеров, может скакать по зубцам этого графика, но в целом будет ползти вниз. Глядя на такое движение мы увидим, что точка в 510-мерном пространстве мечется, но в среднем ползёт более или менее в одну сторону. Давайте же проследим за этими движениями.
Конечно, проследить за движением точки непосредственно в 510-мерном пространстве может не каждый, поэтому мы схитрим. Мы произвольным образом спроецируем это 510-мерное пространство на двумерное пространство экрана. Каждому синапсу присвоим случайный единичный по модулю вектор, и будем суммировать все эти вектора, помноженные на вес синапса. По закону больших чисел сумма окажется недалеко от точки 0. Для начала возьмём случайную необученную сеть и посмотрим, как будет выглядеть траектория, если отмечать точку после каждого отдельного обучающего примера.
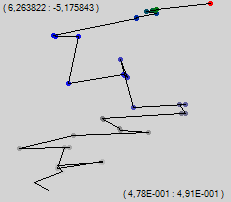
Числа в левом верхнем углу – положение в пространстве левого верхнего угла картинки, а числа справа внизу – это размеры изображаемой области.
Мы видим «броуновское» движение, в котором прослеживается общий тренд вверх. Давайте на ходу поменяем алгоритм. Будем использовать то же самое обратное распространение ошибки, только обучающее изменение будет применяться не всё сразу, а постепенно, на протяжении нескольких шагов. В моей программе я этот метод называю «градиентный спуск медленного обучения». На той же скорости обучения получим ещё 35 точек.

Мы видим, что этот алгоритм обладает гораздо большей плавностью хода. Докинем ещё несколько десятков точек и при большем увеличении увидим, как сеть ползёт по пространству, выискивая в сглаженном рельефе путь.

Сразу понятно, почему второй алгоритм менее склонен к случайным потерям найденных минимумов. Интересно, что на некоторых участках сеть ползёт постепенно, а на некоторых – меняет направление так, словно получила по лбу. Интересно посмотреть, чем эти точки различаются.

На первой картинке мы видим, что сеть медленно, но верно ползёт в одну сторону. Новые точки попадают в область, где сеть и так получает правильный ответ. Кроме того это чисто зелёная область, в которой значение на выходе сети мало зависит от входных данных. Производная от ошибки маленькая, и соответственно управляющее воздействие на сеть невелико. Но вот на второй картинке очередная точка попадает близко к нулю, где у сети большая величина производной от ошибки. К тому же точка находится ниже графика, там ожидается значение -1, а сеть показала там зелёное, судя по цвету, примерно +0,8. Очень большая ошибка совпала с большой производной, сеть получила пинок снизу и пошла по новому пути, вверх. На последней (третьей) картинке видно, что вся синяя область сдвинулась выше. То что направление движения сети по траектории обучения и направление сдвига картинки совпали, конечно же, случайность, но красивая.
Прикажем программе показывать не 50 точек, а 200 и полюбуемся траекторией обучения сети. Рельеф над 510-мерным пространством нам не виден, но в ползании слепой сети по невидимому лабиринту явно угадываются проблемные места – невидимые стенки, о которые то тут, то там стукается сеть, и ползёт в новую сторону.
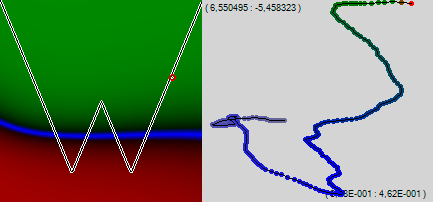
Мы видим, что спустя всего какие-то 200 обучающих примеров левый край нашей разделительной синей линии начал помаленьку загибаться вверх. Вернёмся к классическому алгоритму обратного распространения ошибки («дёрганому») и добавим ещё 200 точек.
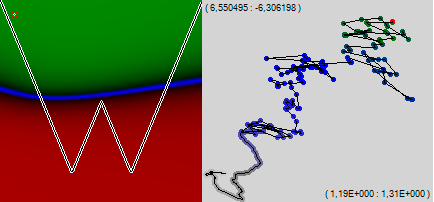
Мы видим, несмотря на то, что сеть начала дёргаться как сумасшедшая, она продолжила двигаться, в принципе, в ту же сторону и, в принципе, с той же итоговой скоростью. Можно довольно живо представить себе тот каньон, по которому сеть ползёт к лучшей жизни, ощупывая стенки. Несмотря на свою 510-мерность, рельеф довольно хорошо прослеживается. А на картинке уже не только левый, но и правый край графика начал загибаться вверх.
Почему же мы видим это монотонное движение? Понятно, что сеть будет учиться, пока края синей линии не станут круто смотреть вверх с обеих сторон. Для этого весам некоторых синапсов потребуется сильно измениться, стать намного больше чем сейчас. Отдельные примеры лишь немного сдвигают их, и потребуется очень много примеров, прежде чем они приобретут свои большие значения. Именно постепенное увеличение веса таких синапсов и тянет траекторию обучения сети по хорошо заметному тренду, в ту сторону, которую мы данному синапсу в самом начале назначили. Синапсы, значения которых в процессе обучения меняются в узком диапазоне, на траектории малозаметны.
Итак, что мы поняли?
Рельеф нельзя увидеть, по крайней мере, это трудно сделать на домашнем компьютере, но по поведению сети можно понять, каков он.
Добавим газу
Давайте продолжим обучать сеть, но каждую следующую точку на траектории обучения рисовать не после каждого одного учебного примера, а после 1000.
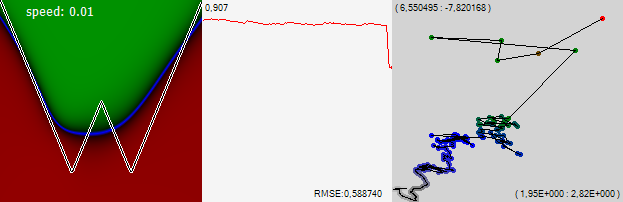
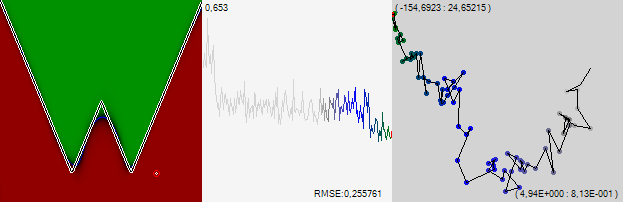
Видно, что сеть в целом продолжила ползти вверх и вправо, загибая края графика вверх. График в средней части рисунка – это среднеквадратическая ошибка за последние 1000 примеров. Одна точка на этом графике соответствует одной точке на траектории обучения на правой картинке. Хорошо видно, как резко начала снижаться ошибка, когда мы прибавили шагу. Цифра в левом верхнему углу графика это масштаб, в котором отображён график, а в правом нижнем углу отображается собственно само значение ошибки.
Итак, продолжим наше путешествие по очень многомерному пространству.
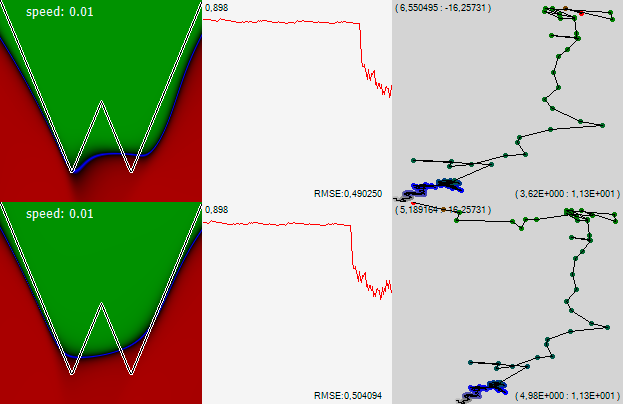
Обратите внимание! В какой-то момент сеть перестала монотонно дрейфовать в одну сторону и затусовалась в одной области. Но потом очередное резкое движение вытолкнуло сеть из этого импровизированного озерца, и она довольно шустро пошла дальше налево. На графике ошибки видно, что на этом участке траектории ошибка была чуть-чуть меньше. Но явно не на столько, чтобы принимать какие-то решения. А, между тем, поглядев на левую картинку можно заметить, что в этом озере сеть научилась понимать, что у графика, который она изучает два минимума. После, ломанувшись влево сеть это знание утратила. Давайте договоримся, что в следующий раз, когда сеть вот так же перестанет монотонно дрейфовать и начнёт внимательнее ощупывать одно интересное ей место, мы предположим, что она чего-то полезного нашла, и снизим скорость, давая ей возможность внимательнее изучить найденное место.
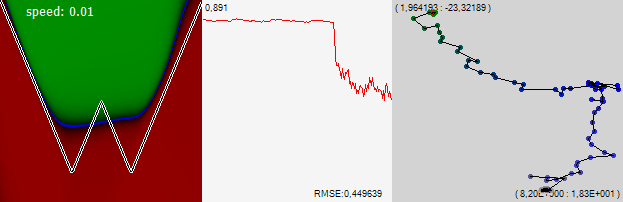
И вот сеть опять начинает внимательно осматривать новое хорошее место. Оно нам нравится, снижаем скорость в 3 раза. Как видим, за свою прозорливость мы были вознаграждены резким улучшением ошибки, а сеть начала искать для себя новое решение уже на ограниченном участочке пространства, в котором, по-видимому, есть хороший локальный минимум.
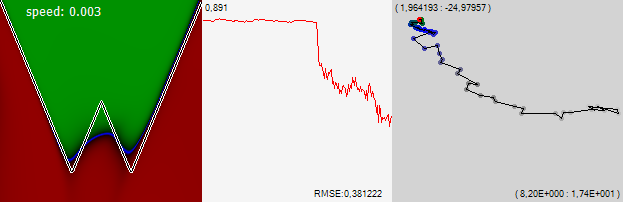
Для закрепления приоритета назову её своим именем: “визуализация kraidiky”, пока кто-нибудь не придумал для неё менее благозвучное и лишённое индивидуальности название.
Итак, какие у нас выводы?
- Наблюдая за траекторией обучения сети, можно чётко различить, когда сеть находится в связанной компактной области локальных минимумов, а когда двигается вдоль градиента по каньону или склону от одной области к другой. Вероятно, понаблюдав за сетью, можно различить и другие особенности невидимого рельефа, по которому путешествует сеть.
- Разница столь заметная, что её можно использовать для принятия решений об изменении режима обучения сети. Изменения в среднеквадратичной ошибке, связанные с этими особенностями рельефа, также наблюдаются, но они очень незначительные, трудноразличимые на фоне шумов и не могут, по всей вероятности, служить основой для принятия решений. Иногда можно видеть даже участки, на которых ошибка сети растёт. Но по визуализациям обоих типов видно, что сеть идёт в выбранном направлении, и находит там значительно более качественные решения, эффект от которых станет заметен позже, как, например, два минимума в нашей задаче.
- Мой алгоритм таков: если сеть перестаёт идти по каньону и начинает изучать ограниченную область, то нужно посмотреть проскакивают ли среди обнаруживаемых в этой области решений хорошие, сильно более хорошие, чем встречались по дороге к этой области. Если да, то уменьшить скорость, позволив сети более внимательно изучить эту область, и, возможно, найти в ней для себя хорошее решение. Если хорошие решения не встречаются, то можно подождать пока сеть сама покинет область и уйдёт из неё по какому-нибудь каньону, или, если поиск затянулся, вытолкнуть её, увеличив скорость.
- Приведенный в статье способ визуализации процесса обучения сети неожиданно информативен. Явно больше, чем наблюдение за средней ошибкой, и порой даже больше, чем сравнение карты полученных знаний с исходной задачей.
- Способ визуализации никак не зависит ни от характера задачи, ни от топологии сети, – может использоваться для визуализации процесса обучения, в том числе и сложно организованных сетей, с трудными задачами, слабо поддающимися визуализации.
В заключение предлагаю вам насладиться зрелищем обучающейся сети. На 1:26 видно как меня не устроила найденная сетью область минимумов, и я отправил её искать другую, просто прибавив скорости обучения.
UPD: У визуализации есть один недостаток. Все синапсы считаются как бы равными по важности. В то время как в реальности это, конечно, не так. Какие-то синапсы очень сильно влияют на конечный результат, какие-то почти никакой роли не играют. Хорошо бы домножать на значимость. Хорошей мерой значимости является производная от ошибки по весу данного синапса. Но проблема в том, что для разных учебных примеров она сильно разнится. Надо бы усреднять по всей учебной выборке, но в моей задаче учебная выборка каждый раз разная и значимость слишком сильно гуляет и зашумляет картинку даже если её усреднять по 1000 последних учебных примеров. ПОка не придумал, как решать эту проблему.
UPD 2: Решил проблему. Беру среднеквадратическое значение производной за всё время обучения. На сотнях тысяч примеров значимость синапсов становится устойчивой и различается для разных синапсов почти на три порядка. Однако, как не странно, такая визуализация оказывается менее информативна. Или информативна по другому, даже не знаю как сказать.
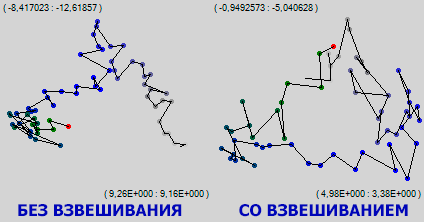
На рисунке запечетлен один и тот же участок обучения сети. Видно, что там, где простая визуализация показала область локальных минимумов, в которой сеть довольно долго тусовалась взвешанная по значимости синапсов визуализация топтания на одном месте не зафиксировала, более того по зелёной части траектории заметен устойчевый дрейф вверх и вправо. Видимо пока сеть в целом топчется в одной небольшой области, она очень интенсивно и осмысленно шевелит своими лучшими синапсами. Как говорится, на клеточном уровне я очень занят.