 Как-то я экспериментировал с клеточными автоматами. С одномерными и двумерными. Придумывал на каком исходном состоянии применить какое-то правило. Когда, в качестве исходного состояния двумерного клеточного автомата я начал использовать бит-реверсивную перестановку диагональной линии, то после применения автомата получались своеобразные узоры. Время от времени среди узоров появлялись явно выраженные характерные паттерны. Я выделил эти паттерны и немного с ними поэкспериментировал. С тем, что мне удалось выяснить, я делюсь в этой статье.
Как-то я экспериментировал с клеточными автоматами. С одномерными и двумерными. Придумывал на каком исходном состоянии применить какое-то правило. Когда, в качестве исходного состояния двумерного клеточного автомата я начал использовать бит-реверсивную перестановку диагональной линии, то после применения автомата получались своеобразные узоры. Время от времени среди узоров появлялись явно выраженные характерные паттерны. Я выделил эти паттерны и немного с ними поэкспериментировал. С тем, что мне удалось выяснить, я делюсь в этой статье.В статье я вкратце расскажу про аддитивные клеточные автоматы. А также приведу последовательность моих наблюдений и задач, которые я ставил. Каждый этап будет сопровождаться изображениями состояния клеточного автомата. Кроме того, для лучшей наглядности, я написал веб-приложение, которое добавит интерактивности при чтении статьи. Приложение основано на React и должно работать в современных браузерах. Также я буду сопровождать некоторые действия ссылками с кусками кода на Python.
Disclaimer: Статья носит чисто информационно-развлекательный характер, поскольку мне не известны приложения предлагаемой информации. Также, мне интересно упорядочить обрывочные сведения, которые мне удалось выяснить. И, возможно, обнаружить в них шероховатости. Возможно, мне придут в голову новые эксперименты.
Надеюсь, что статья развлечет вас, хотя я буду писать четко и по делу.
Предварительное знакомство с клеточными автоматами
Если вы не знакомы с клеточными автоматами (КА) или только слышали о них, то предлагаю ознакомиться с вводными статьями:
Тоффоли Т., Марголус Н., Обзор клеточных автоматов (pdf) на The Game of Life Романа Парпалака — хорошее введение в КА.
Евгений Золотов, Мир в клеточку (pdf) на Компьютерра.
Более практические статьи:
OCo, Клеточные автоматы (pdf) на Программы, фракталы и всякая всячина от OCo — краткое введение в клеточные автоматы и примеры реализации различных клеточных автоматов.
Матвей Котов (mkot), Немного о клеточных автоматах на Хабре.
Татьяна Бибикова, Гидродинамика сперматозоида морского ежа (pdf) — рассказ о научной работе.
Также приведу любопытные, на мой взгляд, материалы на английском:
Elementary Cellular Automaton на WolframMathWorld — описан подход нумерации правил КА и приведены иллюстрации поведения всех правил при некотором стартовом состоянии.
Elementary cellular automaton на Wikipedia — примерно тоже, что и предыдущее. Но приведены иллюстрации применения некоторых правил при случайном стартовом состоянии.
Rafael Espericueta, Cellular Automata Dynamics (pdf) — иллюстрированная книга про нульмерные, одномерные и двумерные КА.
Additive Cellular Automaton на WolframMathWorld — про аддитивные КА.
Mirek Wojtowicz, 1D and 2D Cellular Automata explorer — на сайте есть коллекция правил КА.
Двумерный аддитивный клеточный автомат
У клеточного автомата есть состояние и правило, по которому происходит переход от предыдущего состояния к следующему.
Состоянием двумерного КА является двумерный массив клеток. В нашем случае, этот массив имеет одинаковую длину и ширину N. Каждая клетка может принимать значения 0 или 1. Будем изображать клетки со значением 0 черным цветом, а клетки со значением 1 белым цветом.
Положение клетки в массиве состояния КА описывается координатами [i,j], где i, j принимают значения от 0 до N-1, причем, i — это номер столбца, а j — это номер строки.
Правило — это процедура, которая на основе значения клетки и значения соседних восьми клеток вычисляет значение клетки для следующего состояния. Совокупность клеток, которые могут участвовать в вычислении правила будем называть окрестностью. Так выглядит окрестность клетки [i,j]:
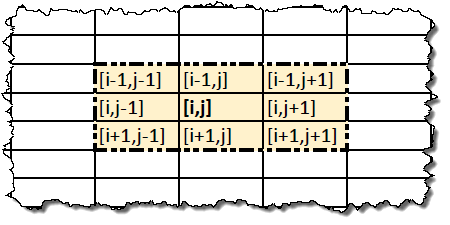
Процедура вычисления правила применяется параллельно и одинаково для всех клеток состояния КА, у которых определены все соседние клетки (в типичной реализации — последовательно с использованием двух массивов состояния.) Однократное применение правила ко всем клеткам будем называть одной итерацией.
На границах состояния КА не все соседние клетки определены. Существуют различные способы определить недостающие клетки. И каждый способ дает отличающийся результат. В нашем случае, недостающие соседние клетки будут взяты с противоположных краев состояния. Таким образом, у нашего массива как бы «склеены» левый край с правым, а верхний край с нижним. Такая «склейка» эмулирует поверхность тора, или еще ее называют тороидальной решеткой.
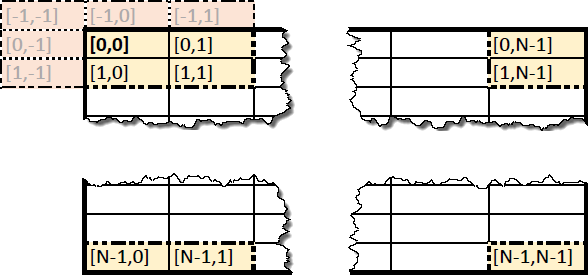 .
.Пожалуй, самым известным примером двумерного КА является игра «Жизнь».
У двумерного аддитивного клеточного автомата (АКА) процедура вычисления правила вычисляет сумму по модулю 2 (тоже, что и XOR) значений определенных клеток из девяти клеток из окрестности вычисляемой клетки. В нашем случае, значение клетки в сумму входит не более одного раза.
Обозначим вычисляемую клетку с координатами [i, j] как c1, а соседние клетки как c2, c4, c8, c16, c32, c64, c128 и c256 с расположением согласно диаграмме:
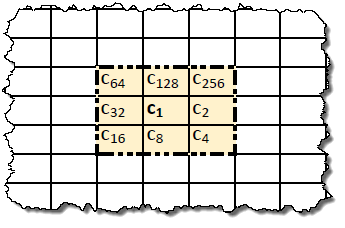
Как вы заметили, индексы клеток окрестности принимают значения вида 2n, где n изменяется от 1 до 9. Такие индексы очень удобны, поскольку сумма произвольных индексов дает число, которое в двоичном представлении однозначно задает какие клетки входят в сумму для вычисления правила. Это число будет номером правила.
Например, правило 15. Согласно двоичному представлению 15=0000011112, оно раскладывается на слагаемые 0000000012, 0000000102, 0000001002, 0000010002 или 1, 2, 4 и 8. Отсюда, правило 15 значит, что каждая клетка нового состояния является суммой клеток с1, с2, с4 и с8 предыдущего состояния. Другие соседние клетки не участвуют в вычислении правила. Таким образом, процедура вычисления правила будет выражением с1[t]=с1[t-1]+с2[t-1]+с4[t-1]+с8[t-1] (mod 2), где с1[t] — клетка нового состояния, а с1[t-1], с2[t-1], с4[t-1], с8[t-1] — клетки предыдущего состояния, причем координаты клеток с1[t] и с1[t-1] совпадает, а клетки с2[t-1], с4[t-1], с8[t-1] являются соседними клетками клетки с1[t-1] в соответствии с диаграммой.
Идея такой нумерации правил АКА взята из [Khan1997].
В приложении вы можете интерактивно задавать правило, как по номеру, так и отмечая флажки с клетками окрестности. При изменении одного представления другое представление будет изменятся автоматически.
Весь материал статьи основан на использовании правила 15. Также, будет пара экспериментов с применением правила 511.
Предварительное опознание проявления перестановки диагональной линии
Возьмем пустое состояние АКА 64x64 клетки, и нарисуем диагональную линию:
 .
.Применим бит-реверсивную перестановку строк. Или столбцов. Без разницы. Что такое реверс битов и бит-реверсивная перестановка я уже писал. [BRH2012] В приложении это делается кнопкой BRP(y) или выбрав Pattern «Permuted Diagonal Line». Получим состояние:
 .
.Теперь будем итеративно применять к этому состоянию правило 15 (кнопка «Apply rule».) После 30 итераций получим состояние:
 .
.Мой глаз уже наметан, и я легко узнаю искомые паттерны. Из этого состояния можно выделить нечто имеющее размер 8x8 состоящее из виртуальных черных и белых клеток, повторяющееся четыре раза с различными способами прорисовки. Выделим это в явном виде:
 .
.Казалось бы, какой-то набор клеток. Ведь, каждая итерация дает определенный рисунок. Почему я выделил именно эту итерацию и этот рисунок?
Давайте возьмем АКА 128x128 клеток. И проделаем тоже самое. Остановимся на итерации 62. Видим состояние:
 .
.Эксперимент без комментариев
Понажимайте кнопки перестановок BRP(x, y) и 4BRP(x, y) в разной последовательности. Аналогичных перестановок можно добиться кнопкой PG(x, y). Таким образом можно получить паттерн в чистом виде без распознавания виртуальных клеток.
Видим виртуальные клетки, которые задают паттерн размером 16x16. Выделим его:
 .
.Чтобы окончательно убедиться, возьмем АКА 256x256 клеток. Вот состояние на итерации 60:
 .
.Видим виртуальные клетки, задающие знакомый паттерн 8x8 клеток. Отличается лишь способ прорисовки виртуальных клеток. На следующих итерациях паттерн повторяется в том или ином способе прорисовки. Например, итерация 62:
 .
.Наконец-то, итерация 126:
 .
.Узнаваемая картина, не правда ли? Также, обратите внимание на динамический муар при плавном движении этого рисунка на вашем LCD-мониторе. Но это тема для другой статьи. Выделим из виртуальных клеток паттерн 32x32:
 .
.Мне этого было достаточно, чтобы меня охватил интерес к этому объекту и глубже его исследовать. Назовем этот объект проявлением перестановки диагональной линии или ППДЛ.
Я решил разобраться как генерировать такие паттерны в чистом виде не делая множество итераций АКА и не распознавая виртуальные клетки.
Генерация проявления перестановки диагональной линии
Возьмем ППДЛ в чистом виде 32x32 клетки. Применим к нему правило 15 (с самого начала я экспериментировал только с правилом 225, что приводило к возникновению лишних поправок при генерации ППДЛ.) Получим состояние:
 .
. Если немного повозиться с этим состоянием, то можно прийти к тому, что в каждой четверти изображена бит-реверсивная перестановка диагональной линии. Проверим это нажатием кнопки 4BRP(y). Получим:
 .
.Также, можно не переставлять каждую четверть отдельно, а переставить строки состояния целиком. Тогда получится две диагональные линии. Казалась бы, нет никакой разницы какой подход выбрать. Но, при переходе к произвольному модулю/основанию, с первым вариантом генерация получается проще. (С самого начала, в своих экспериментах, я пользовался вторым способом. А к первому способу я окончательно пришел в прямо при написания статьи.)
И так, нам известно состояние АКА после применения правила 15. И такое состояние легко сгенерировать для заданного размера.
Осталось обратить вспять это состояние. Распишем правило 15 еще раз:
с1[t]=с1[t-1]+с2[t-1]+с4[t-1]+с8[t-1] (mod 2), где с1[t] — известная клетка состояния, содержащего перестановки диагональных линий в каждой четверти, а с1[t-1], с2[t-1], c4[t-1], с8[t-1] — неизвестные клетки ППДЛ. Если посмотреть на обнаруженные ППДЛ различных размеров, то нетрудно заметить, что клетки первой строки и первого столбца содержат только нули. Таким образом, будем считать, что значение первых клеток ППДЛ мы уже знаем. Отталкиваясь от этих значений, становится возможным найти остальные значения клеток ППДЛ.
Например, возьмем АКА 8x8 клеток. Состояние t с перестановками диагональных линий в каждой четверти изобразим в виде таблицы:

Изобразим в виде таблицы искомое состояние ППДЛ t-1 с известными первой строкой и первым столбцом:

Три известные клетки в левом верхнем углу будут соответствовать слагаемым правила 15: с1[t-1], с2[t-1], с8[t-1]. Неизвестной клетке [1,1] соответствует слагаемое с4[t-1]:
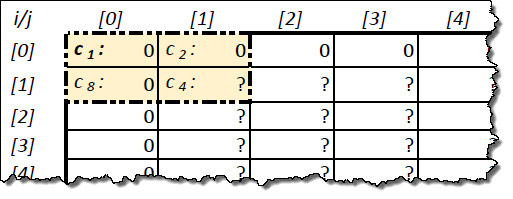 .
.Другие слагаемые в правиле 15 не задействованы.
Решим уравнение для с4[t-1]. Получим:
с4[t-1] = с1[t]+с1[t-1]+с2[t-1]+с8[t-1] (mod 2) (при сложении по модулю 2 знак минус не имеет значения.) Согласно таблицам, с4[t-1] = 1 + 0 + 0 + 0 = 1 (mod 2). Получим состояние:

Аналогичным образом, вычисляется клетка [1, 2] или клетка [2, 1] с учетом смещения:
 .
.И т.д. Клетка за клеткой, строка за строкой, мы получим состояние:

* * *
Также, ППДЛ можно генерировать с помощью блочно-рекурсивного построения матриц. Если это кому-то интересно, то может попробовать сделать это самостоятельно.
Некоторые свойства проявления перестановки диагональной линии
Свойство 1
ППДЛ имеет размер N равный степени двойки, т.е. N=2n.
Свойство 2
Клетки первой строки и первого столбца равны нулю.
Свойство 3
Четные клетки на строке N/2 и столбце N/2 равны единице, а нечетные равны нулю. Другими словами, они равны соответствующей координате клетки, взятой по модулю 2.
Свойство 4
Если к ППДЛ применить правило 15, то мы получим состояние, которое содержит перестановки диагональной линии в каждой четверти.
Свойство 5
Подготовим ППДЛ 64x64 клетки:
 .
.И будем применять правило 511. На итерации 16 мы получим:
 .
.Это тот же паттерн, только смещен на 32 клетки по диагонали.
Аналогичная картина происходит с ППДЛ других размеров.
Полученный таким образом паттерн можно генерировать также, как и основной, только нужно взять первую строку и первый столбец, которые состоят из единиц на четных клетках.
Следует заметить, что это не уникальное свойство данного паттерна. Можно придумать и другие состояния АКА, которые имеют такое же свойство.
Если дальше применять правил 511, то на итерации 32 вернется исходное изображение. Исходное изображение восстанавливается при любой комбинации клеток состояния АКА, но не при любом размере состояния. Это свойство правила 511 предлагают применять в криптографии. [Chatz2012] Из этого источника я и узнал о возможности использовать правило 511 в своих экспериментах.
* * *
Исследуя другие области, я столкнулся с тем, что если есть объекты, в которых применяются вычисления с модулем 2, то их можно расширить на произвольный модуль >= 2.
Проявление перестановки диагональной линии с произвольным модулем/основанием
Сначала, расширим процедуру вычисления правила. Теперь, вычисления правила будет вычислять сумму выбранных клеток окрестности взятую по модулю M>=2. Т.е., после того как мы вычислим сумму значений выбранных клеток, в качестве итогового значения клетки будем брать остаток от деления на число M. Благодаря вычислению по модулю M, клетки состояния АКА будут принимать целочисленные значения от 0 до M-1.
Клетки со значением 0 так и будем изображать черным цветом, клетки со значением M-1 будем изображать белым цветом, а промежуточные значения клеток будем изображать промежуточными оттенками серого цвета.
Кое-что об АКА с модулем >= 2 есть в [CAD1997].
Также, нужно перейти от реверса битов, который является реверсом цифр с основанием 2, к реверсу цифр с произвольным основанием B>=2. Реверс цифр позволит произвести цифро-реверсную перестановку диагональной линии (не совсем уверен, что правильно ввел термины. Думал насчет вариантов: реверс цифр/дигитов и дигит-реверсивная перестановка. Но, по-моему, это выглядит ужасно.) Еще будет некорректно, если размер состояния АКА будет степенью 2. Нужно скорректировать размер состояния АКА. Теперь этот размер N будет некоторой степенью основания B, т.е. будет иметь вид N=Bn.
Поэкспериментируем с правилом 15. Модуль и основание должны совпадать. Раз. Два.
Во втором случае на итерации 62 проявилось что-то отдаленно похожее:
 .
.Есть виртуальные клетки, но все это не то.
Наткнулся в при написании статьи...
На итерации 125 появляется такое состояние:

Если три раза применить перестановку PG(x,y), то получим фрагменты с искомым паттерном:


Если три раза применить перестановку PG(x,y), то получим фрагменты с искомым паттерном:

Потом я попробовал правило 511. Возьмем перестановку диагональной линии с модулем/основанием 3 и размером 243x243. На итерации 26 получим:
 .
.Четко видны виртуальные клетки 5x5 (правильней 6x6), и узнаваемый паттерн:
 .
.Возьмем перестановку диагональной линии с модулем/основанием 3 и размером 729x729. На итерации 80 получим виртуальный паттерн размером 18x18.
Аналогичные результаты можно получить, если взять перестановку диагональной линии с модулем/основанием 4. Но для этого придется вычислять правило с окрестностью размером 4x4, что не реализовано в приложении. Могу лишь показать готовые результаты. На итерации 42 получим виртуальный паттерн размером 8x8.
Попытаемся найти способ генерирования ППДЛ как мы это делали раньше.
Возьмем ППДЛ 18x18 клеток с модулем/основанием 3:
 .
.Применим правило 15 и получим ужасную кашу:
 .
.Начнем с начала. Применим правило 511:
 .
.Уже лучше. Но все равно много лишнего. И не охота обращать состояние вспять по правилу 511.
Через некоторое время мне пришла в голову идея поэкспериментировать со знаками слагаемых правила АКА. Чтобы обозначить какие слагаемые применяются со знаком минус, я предлагаю после номера правила писать еще один номер, в котором используется такое же кодирование, как и у правила.
Например, правило 15-10. В него входят слагаемые c1, c2, c4, c8. Но слагаемые c2 и c8 входят со знаком минус. Получим функцию с1[t]=с1[t-1]-с2[t-1]+с4[t-1]-с8[t-1] (mod M)
Правило 15-5 дает состояние:
 .
.А правило 15-10 дает состояние:
 .
.Остановимся на правиле 15-10. Поскольку в левой верхней четверти клетки содержат единицы (серые клетки.) Тогда как после правила 15-5 — двойки (белые клетки.) А единица ближе к началу числовой оси.
Применим цифро-реверсивную перестановку строк в каждой четверти последнего состояния кнопкой 4DRP(y) и получим:
 .
.Состояние можно разделить на четверти, и в каждой из них диагональная линия с соответствующим значением.
И так, нам стало известно состояние, которое нужно получить после применения правила 15-10. Осталось обратить вспять это состояние. Распишем правило 15-10:
с1[t]=с1[t-1]-с2[t-1]+с4[t-1]-с8[t-1] (mod M), где с1[t] — известная клетка состояния, содержащего перестановки диагональных линий в каждой четверти с соответствующим значением, а с1[t-1], с2[t-1], c4[t-1], с8[t-1] — неизвестные клетки ППДЛ, M — модуль (на данный момент он равен 3.) Зафиксируем значения с1[t-1], с2[t-1], с8[t-1] как это мы делали ранее. Решим уравнение для с4[t-1]. Получим:
с4[t-1] = с1[t]-с1[t-1]+с2[t-1]+с8[t-1] (mod M). Вычислив все неизвестные клетки мы получим искомый паттерн.
Таким образом, получение паттернов с модулем/основанием M >= 2 происходит аналогично. Нужно взять состояние, четверть которого имеет размер, в виде степени основания. В каждой четверти нарисовать диагональные линии с цифро-реверсивной перестановкой. В левой верхней и правой нижней четверти клетки принимают значение 1. А две другие четверти принимают значение M-1. Затем обратить вспять полученное состояние по правилу 15-10. Исходный код.
Единственное что смущает, что паттерн был выявлен с помощью правила 511-0. Чтобы удостовериться в правильности догадок проверим правило 15-10 на перестановленной диагональной линии. На итерации 52 получим:
 .
.Картина идентична полученной ранее с помощью правила 511-0 с точностью до смещения.
Этого смещения не было бы...
Если немного изменить способ вычисления правила 511. Сейчас мы вычисляем правило 511 в окрестности с основной клеткой по центру. А в правиле 15-10, с учетом только задействованных клеток, основная клетка лежит в углу. Мы можем устранить эту разницу, изменив вид окрестности для правила 511 таким образом:

Вот куски кода, которые реализуют описанные варианты:

Вот куски кода, которые реализуют описанные варианты:
- вычисление с правилом 15-10;
- вычисление с правилом 511 (центровая окрестность);
- вычисление с правилом 511 (угловая окрестность.)
Эксперименты с другими размерами состояния АКА с применением правила 15-10 дают паттерны с виртуальными клетками, которые совпадают с ППДЛ, которое генерируется приведенным алгоритмом.
* * *
Мне также, удалось реализовать генерацию ППДЛ с основанием/модулем 3 с помощью блочно-рекурсивное построение матриц. Исследуя блочную структуру ППДЛ, я заметил, что структура блоков становиться все сложнее с увеличением модуля/основания. Также становится заметным элемент похожий на матрицу дискретного преобразования Фурье (т.е. матрица в виде таблицы умножения по модулю.) Но я не хочу перегружать эту статью подробным исследованием в этом направлении. Может кому-то будет интересней изучить это самостоятельно.
* * *
Пересмотрим свойства ППДЛ.
Некоторые свойства проявления перестановки диагональной линии с модулем/основанием >= 2
Свойство 1
ППДЛ имеет размер N равный удвоенной степени основания B, т.е. N=2·Bn. К этому свойству добавился еще один параметр B. Четверти состояния стали явно выраженными.
Свойство 2
Клетки первой строки и первого столбца равны нулю. Это свойство без изменений.
Свойство 3
Клетки на строке N/2 и столбце N/2 равны соответствующей координате клетки, взятой по модулю M. К этому свойству добавился еще один параметр M.
Свойство 6
Если к ППДЛ применить правило 15-10, то мы получим состояние, которое содержит перестановки диагональной линии в каждой четверти. Перестановки в левой верхней четверти и в правой нижней четверти принимают значение 1, а перестановки в двух других четвертях принимают значение M-1. Это свойство стало параметрическим. Кроме того, процедура вычисления правила содержит знаки минус при слагаемых.
Свойство 5
Я подбирал правило АКА для этого свойства и пока нашел правило 511-510.
Если модуль/основание равны трем, то свойство выполняется и появляется промежуточный паттерн:
 .
.Но это свойство не всегда выполняется, если модуль/основание больше трех.
Свойство 6
С правилом 15-0 это свойство не рассматривалось, т.к. оно не наблюдалось. С использованием правила 15-10 стало возможным получить ППДЛ без модуля вообще (в построении перестановок диагональных линий модуль M может приравниваться 0.) В приложении можно задать модуль соответствующий максимальному значению клетки без модуля. Получим ППДЛ в такой форме:
 .
.Альтернативно применение правила 15-0 и 15-10
Если нарисовать произвольный контур или совокупность точек и обратить состояние по правилу 15-10 при достаточно большом модуле, то получится некоторый градиентный рисунок. Например, диагональная линия (нажмите Reverse rule.)
Используя постепенное перемещение контуров и обращение правила 15-10 создал различные абстрактные анимации и выложил их на YouTube. В описании под каждым видео прилагается ссылка на исходные код.
Интересный результат получится если обратить перестановку диагональной линии по правилу 15-0, причем, начальные значения клеток первой строки и первого столбца равны соответствующей координате клетки:
.
При создании этого видео также применяется правило АКА побитово и другие манипуляции.
Рассмотрим, что получается при обращении по правилу 15-0 без модуля:
 .
.Вид неказистый. Заметно чередование клеток. Учтем это.
Предлагаю последовательно прорисовать (там два файла) все значение, которые принимают клетки полученного состояния. Для наглядности, при увеличении значения, предыдущие значение будет постепенно угасать. Клетки с четными и нечетными координатами будут изображены различными цветами:
 .
.Хорошо виден контур, который проявляется в видео.
Описание функций веб-приложения
Приложение опубликовано на GitHub. Оно полностью реализовано на JavaScript с использованием React. Это мой первый проект на JavaScript. Его работа проверялась в Internet Explorer 11, FireFox 30.0 и эпизодически в Chrome 35.0. В Internet Explorer отсутствует редактор числовых полей, не работает скрытие элементов выпадающего списка. В IE и Chrome действуют заблокированные кнопки.
Благодаря React, очень удобно разрабатывать приложение. В особенности, это касается динамического изменения элементов пользовательского интерфейса.
Кратко пройдусь по всем элементам приложения.
Base — основание для некоторых элементов приложения и вычислений. Число от 2 до 4096.
Modulus — модуль для некоторых вычислений. Число от 2 до 4096.
State size — размер состояния АКА. Некоторые элементы списка зависят от основания (base) и имеют вид basen.
Scale — масштаб отображения состояния АКА. Размер и масштаб в совокупности ограничены 4096 пикселями, чтобы случайно не возникло жутких висов браузера.
Pattern — шаблоны начальных состояний АКА. О них будет написано ниже.
Apply rule — применить правило АКА и отобразить следующее состояние. Результат вычислений следующего состояния зависит от модуля, правила, знака правила и от текущего состояния.
Reverse rule — вычислить предыдущее состояния АКА приняв клетки первой строки и первого столбца искомого состояния равными нулю. Вычисление искомого состояние зависят от модуля, от правил и знаков с индексами 1, 2, 4, 8 и от текущего состояния. Причем правило с индексом 4 обязательно должно присутствовать. Интересные результаты получаются при выборе шаблона «Manifestation of PDL» и правила 15-10.
BRP(x,y)/DRP(x,y) — бит-реверсивная (цифро-реверсивная) перестановка строк и столбцов состояния АКА. Вид перестановки зависит от основания (base.) Кнопка активна если размер состояния АКА является степенью основания (state size=basen.) Для удобства после применения перестановки кнопка подсвечивается желтым цветом. Поскольку повторная перестановка возвращает исходное состояние, то при повторном нажатии подсветка будет убрана.
BRP(y)/DRP(y) — бит-реверсивная (цифро-реверсивная) перестановка строк. Все остальное аналогично. Добиться перестановки столбцов можно добиться последовательным нажатием DRP(x,y) и DRP(y).
4BRP(x,y)/4DRP(x,y) и 4BRP(y)/4DRP(y) — бит-реверсивная (цифро-реверсивная) перестановка строк и/или столбцов четвертей состояния АКА. Кнопки активны если размер состояния АКА является удвоенной степенью основания (state size=2·basen.) Все остальное аналогично.
PG(x,y)/PG(x) — Pattern Grouping. Перестановка вида [0 1 2 3 4 5 6 7 8] -> [0 2 4 6 1 3 5 7] (при основании 2.) Кнопки активны если размер состояния АКА является степенью основания (state size=basen.) Перестановка является циклической. Длина цикла равна этой самой степени n, т.е. n=logbase(state size). В конце цикла возвращается исходное состояние. В квадратных скобках отображается количество применений перестановки в цикле. Интересно наблюдать эту перестановку при любых бит/цифро-реверсных паттернах.
Откуда берется эта перестановка?
Эта перестановка была выявлена в процессе написания статьи при последовательно применении перестановок BRP и 4BRP. Но эти кнопки активны вместе только, если размер состояния является степенью 2 (state size=2n.) Хотя перестановка pattern grouping может быть расширена на размер яляющийся степенью любого числа (state size=basen.) При непосредственной реализации этой перестановки появилось больше итераций этой перестановки, которые не наблюдались при совместном использовании перестановок BRP и 4BRP.
Rule # — задает какие слагаемые участвуют в процедуре вычисления правила АКА как по номеру, так и с помощью флажков, которые соответствуют клеткам окрестности. Число от 0 до 511.
Sign # — задает знаки соответствующих слагаемых процедуры вычисления правила. Число от 0 до 511. При значении 0 все слагаемые положительны. Если какой-то флажок отмечен, то соответствующее слагаемое берется со знаком минус. Когда модуль равен 2, то знаки не имеют значения.
Подсказка Rule/Sign — активно реагирует на изменения правила. Ноль означает, что соответствующее слагаемое не участвует в правиле. Плюс — положительное слагаемое. Минус — отрицательное слагаемое.
Rule bits layout — шпаргалка по индексам правила, которые в сумме составляют номер правила.
Make image — создает копию текущего состояния АКА в виде картинки, которую можно сохранить на диск по клику по ней правой кнопкой мыши. Также удобно использовать, если нужна копия состояния АКА для визуального сравнения со следующими итерациями.
Шаблоны из списка «Pattern»
(unknown) — устанавливается после любых изменений.
Empty — все клетки состояния АКА устанавливаются в 0.
Diagonal Line — диагональная линия. Значение устанавливаемых клеток равно 1.
Permuted Diagonal Line (PDL) — диагональная линия после бит-реверсивной (цифро-реверсивной) перестановки строк. Вид перестановки зависит от основания (base.) Размер состояния АКА должен быть степенью основания (basen.) Значение устанавливаемых клеток равно 1.
Quarter Permuted Diagonal Line (QPDL) — диагональная линия в правой нижней четверти состояния АКА после бит-реверсивной (цифро-реверсивной) перестановки строк в четверти. Вид перестановки зависит от основания (base.) Размер состояния АКА должно быть (удвоенной) степенью основания (state size in [basen, 2·basen].) Если размер не удвоенный, то он будет удвоен автоматически. Значение устанавливаемых клеток равно 1. При некоторых значениях модуля/основания после некоторого количества итераций применения правила 15-10 будет получено ППДЛ.
Manifestation of PDL — ППДЛ. Вид паттерна зависит от основания (base) и модуля (modulus.) Размер состояния АКА должно быть (удвоенной) степенью основания (state size in [basen, 2·basen].) Если размер не удвоенный, то он будет удвоен автоматически. Клетки принимают значения от 0 до modulus-1. Эксперименты можно начать с одинаковым основанием и модулем.
Exclusive Or — генерация паттерна побитового XOR координат клеток. Итоговое значение клетки берется по модулю (modulus.) Клетки принимают значения от 0 до modulus-1. Эксперименты можно начать с одинаковым модулем и размером состояния АКА.
Modular Multiplication — генерация паттерна умножения координат клеток. Итоговое значение клетки берется по модулю (modulus.) Клетки принимают значения от 0 до modulus-1. Эксперименты можно начать с одинаковым модулем и размером состояния АКА. Этот паттерн встречается в дискретном преобразовании Фурье.
Random — генерация случайного состояния АКА. Клетки принимают случайные значения от 0 до modulus-1.
Источники
[BRH2012] grep, Голографические свойства бит-реверсивной перестановки, 2012.
[Khan1997] A.R. Khan, et.al., VLSI architecture of a cellular automata machine, 1997.
[Chatz2012] Savvas A. Chatzichristofis, et.al., Encryption Using the Recursive Attributes of the eXclusive-OR Filter on Cellular Automata, 2012.
[CAD1997] Rafael Espericueta, Cellular Automata Dynamics, 1997.