Вдохновившись недавней публикацией «Персистентное декартово дерево по неявному ключу», решил написать про реализацию персистентной очереди. Те, кто подумал сейчас, что раз обычная очередь — структура тривиальная, то и её персистентный вариант должен быть очень простым, ошиблись, получающаяся реализация как минимум не проще, чем для вышеуказанного дерева.
Реализовывать мы будем, естественно, так называемую полную персистентность — это значит, что промежуточные версии доступны не только в режиме read-only и мы можем в любой момент времени добавлять и извлекать из них элементы. Кроме того, нам, конечно, хотелось бы иметь такую же асимптотику времени работы и дополнительной памяти, как и для неперсистентного варианта, а именно O(n), где n — суммарное количество операций, совершаемых с нашей очередью. К слову, если ослабить требования до O(n log n), то очередь тривиально эмулируется с помощью персистентного декартового дерева по неявному ключу.
Примем следующий простой интерфейс работы с нашей структурой данных: получающиеся в результате запросов версии очередей будем нумеровать целыми неотрицательными числами, изначально имеется лишь пустая очередь под номером 0. Пусть у нас есть N версий очередей (включая исходную пустую), тогда они занумерованы числами от 0 до N-1 и мы можем выполнить следующие четыре запроса:
Как известно, персистентный стек — очень простая структура данных и асимптотика у него та, что нам и нужна. Кроме того, мы знаем, что очередь можно имитировать с помощью двух стеков. Возникает очевидная идея: сделаем эти два стека персистентными и задача решена! К сожалению, такой простой подход не сработает. Все дело в том, что при данной имитации у нас не всякая операция имеет асимптотику O(1): если при pop’е стек, из которого мы достаем элементы, оказывается пустым, то мы перекладываем в него все элементы из другого стека. В случае с обычным очередью каждый элемент перекладывается только один раз, поэтому суммарная асимптотика остается O(n), но в персистентном случае каждый элемент может принадлежать многим очередям и соответственно быть переложен несколько раз. Пусть, например, q — номер очереди, у которой этот стек пустой, тогда после push(q, 1) и push(q, 2) у полученных очередей этот стек останется пустым и при pop’е из них каждый элемент очереди q будет переложен по два раза. Организовать же какое-либо совместное использование переложенных элементов невозможно в силу того, что самые нижние элементы у полученных перекладыванием стеков будут различны (1 и 2 соотвественно), а персистентный стек устроен таким образом, что каждый элемент хранит указатель на элемент, лежащий ниже его, поэтому в любом случае мы будем вынуждены иметь 2 копии предпоследнего элемента, которые будут указывать на соответствующий последний, а значит и 2 копии предпредпоследнего, чтобы указывать на нужный предпоследний и так далее по цепочке.
Тем не менее существует алгоритм, основанный на такой идее (имитации очереди с помощью двух стеков), гарантирующий, что стек, из которого мы достаем при pop’e, никогда не окажется пустым и использующий для обеспечения этого 6 стеков. Мой же алгоритм эту идею в явном виде не использует, хотя при общие моменты, конечно, найти можно.
Попытаемся использовать ту же структуру, что и при реализации персистентного стека: будем хранить добавляемые элементы в виде дерева (точнее говоря, набора деревьев — леса), в каждой вершине будет лежать добавленный элемент и указатель на предшествующий ему в очереди (точнее, на соответствующую этому предшествующему элементу вершину дерева). Говоря в дальнейшем элемент очереди, я часто буду подразумевать именно соответствующую элементу вершину.
Непустая очередь в таком случае может быть представлена парой указателей на первый и последний элемент очереди, причем вершина, соответствующая первому элементу, обязательно будет предком вершины, соответствующей последнему (ну или совпадать с ней в случае очереди из одного элемента). Пример такой структуры и отображения в ней очереди:
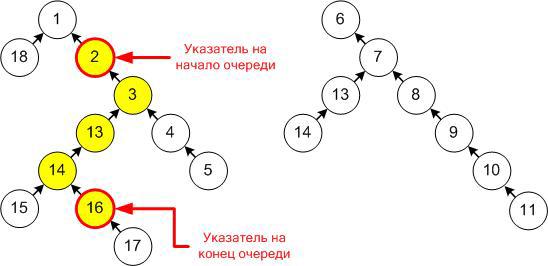
Заметим, что операция push просто создает новую вершину, устанавливая ей в качестве родителя последний элемент исходной очереди (либо она становится новым корнем, если добавляли в пустую), а операция pop наш лес вообще не трогает, просто сдвигает указатель на первый элемент. Тем самым, после создания вершина остается неизменной до конца работы и можно не переживать, что новые операции могут каким-либо образом испортить уже существующие очереди.
Наша единственная проблема при таком подходе – это реализация операции pop (остальные три — тривиальны), непонятно, как определить на какую вершину сдвинуть указатель на первый элемент, ведь для вершины мы храним лишь указатель на родителя, но не на сыновей (коих у одной вершины может быть несколько штук, и, даже если их все хранить, совершенно неясно, какой из них соответствует следующему элементу нашей очереди). Поэтому для каждой очереди, в которой больше двух элементов, будем дополнительно хранить указатель на элемент некоторого односвязного списка, такого, что элемент списка по нашему указателю содержит указатель на второй элемент нашей очереди, а элементы, лежащие ниже его по списку, указатели на третий, четвертый и так далее соответственно. Имея такой указатель для исходной очереди, при выполнении pop'а нам не составит теперь труда определить новую голову очереди, а указатель на такой элемент списка для получившейся очереди – это просто указатель на следующий элемент в данном списке.
Однако, по причинам, аналогичным тем, по которым эмуляция очереди двумя стеками не работает, добиться того, чтобы для каждой очереди ниже по списку лежали абсолютно все её промежуточные вершины, у нас не выйдет, поэтому, пускай, в нем будут лежать только сколько-то первых из них, а мы, когда этот список начнет становиться слишком маленьким, будем строить новый список, продвигаясь шаг за шагом (то есть увеличивая строящийся список на 1 элемент с каждой операцией push или pop) с конца очереди в начало, идя по указателям на родителей вершин нашего дерева и стараясь, чтобы к моменту, когда старый список закончится, у нас уже был новый наготове.
Говоря более формально, для каждой очереди помимо указателей на начало и конец и указателя на элемент уже готового списка будем хранить ещё и указатель на элемент строящегося списка (в случае, если мы ничего не строим, он будет равен 0) и вычислять его значение для новой очереди (полученной после применения к исходной push’a или pop’a) по следующему простому алгоритму:
При этом ни сам исходный элемент списка, ни указатель на него, хранящийся для исходной очереди, мы менять не будем, и вообще, у нас все данные (вершины дерева, элементы списков, данные, хранящиеся для очередей) будут иммутабельны (то есть после создания никогда не будут менять своего значения). Изображение того, как это всё устроено и что происходит при push’e или pop’e, можно увидеть на схеме (сделать её более понятной не получилось, сколько ни старался):
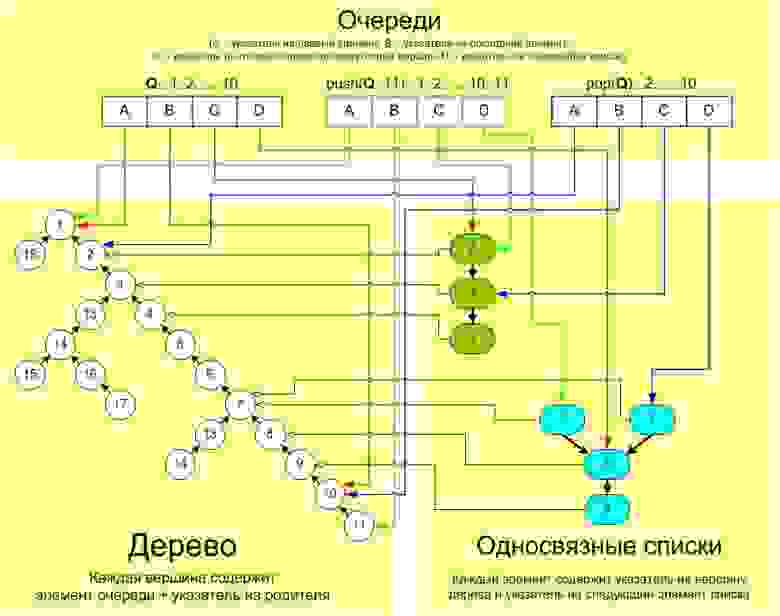
Соответственно, если при достройке списка мы доходим до первого промежуточного элемента, то конструирование для этой очереди завершено (при этом какие-то другие очереди могут продолжать достраивать этот список, но так как старые элементы никогда не меняются, нам это никак не навредит). В таком случае на место указателя на элемент старого списка записываем указатель на элемент нового, а указатель на конструируемый список присваиваем нулю.
Из описания алгоритма видно, что при выполнении каждого запроса мы создаем не более одной новой вершины дерева и не более одного нового элемента списка и тратим на выполнение O(1) времени, то есть асимптотика та, которой мы и добивались, и осталось лишь обсудить правильный критерий.
Будем действовать следующим образом: пока размер нашего списка больше либо равен 1/2 от количества промежуточных вершин (то есть вершин без первой и последней), мы ничего не предпринимаем, как только станет меньше, начинаем конструировать новый. Заметим, что если промежуточных вершин нет, то мы имеем неравенство 0 ≥ 0 и ничего не делаем, то есть в особый случай это выделять не нужно. Докажем, что при таком подходе мы никогда не окажемся в ситуации, когда старый список кончился, а новый ещё не готов.
Для начала докажем следующий инвариант: если мы конструируем новый список, то на каждом шаге 2k + l = s, где k — количество элементов в старом списке, l — в конструируемом (после уже выполненной на этом шагу достройки), s — суммарное количество промежуточных элементов. Доказывать будем методом математической индукции. Рассмотрим первый шаг, когда мы только начали конструирование (l = 1). Заметим, что для новой очереди 2k – s < 0 (наш критерий), однако для исходной 2kold – sold ≥ 0. Посмотрим, как такое могло случиться: если наша операция push, то k = kold, а s = sold + 1, а если pop, то k = kold – 1 и s = sold – 1. Как нетрудно заметить, в обоих случаях 2k – s меньше 2kold – sold ровно на единицу и, так как обе разности — целые числа, значит, вторая из них 0, а первая -1, следовательно, 2k + 1 = s, а наше l как раз единица и есть. База индукции доказана. Докажем переход: пусть на каком-то шаге конструирования 2kold + lold = sold. Тогда l = lold + 1 (достроили список на 1 элемент), в случае push’a: k = kold, s = sold + 1, в случае pop’a: k = kold – 1, s = sold – 1. В обоих случаях равенство выполняется, а значит утверждение доказано.
Предположим теперь, что мы делаем операцию pop, а у исходной очереди нужный нам список пустой (при push’е мы этот список никак не используем). Тогда может быть одно из двух:
Осталось лишь доказать, что, когда мы заканчиваем конструирование, условие отсутствия конструирования выполняется, то есть длина получившегося списка не меньше 1/2 от общего количества промежуточных вершин, иными словами, что в момент завершения 2l ≥ s или, что равносильно, l ≥ s – l. Но что такое s – l? Это количество промежуточных вершин, которые не содержатся в нашем списке. Нетрудно понять, что оно равно количеству операций push, произошедших в процессе конструирования. Однако при каждой такой операции количество элементов в нашем списке также увеличивалось на 1 (возможна ситуация, когда на предыдущем шаге элемент конструируемого списка соответствует третьему по счету элементу очереди и мы делаем pop, тогда для новой очереди элемент списка начинает соответствовать первому промежуточному элементу сразу без достройки, но такое возможно только на последнем шаге конструирования и только при операции pop). Поэтому l ≥ количества таких push’ей (не трудно понять, что даже строго больше), что нам и требовалось доказать.
Для наглядности, продемонстрируем, что происходит в двух крайних случаях: когда мы все время выполняем pop и когда все время push'им:
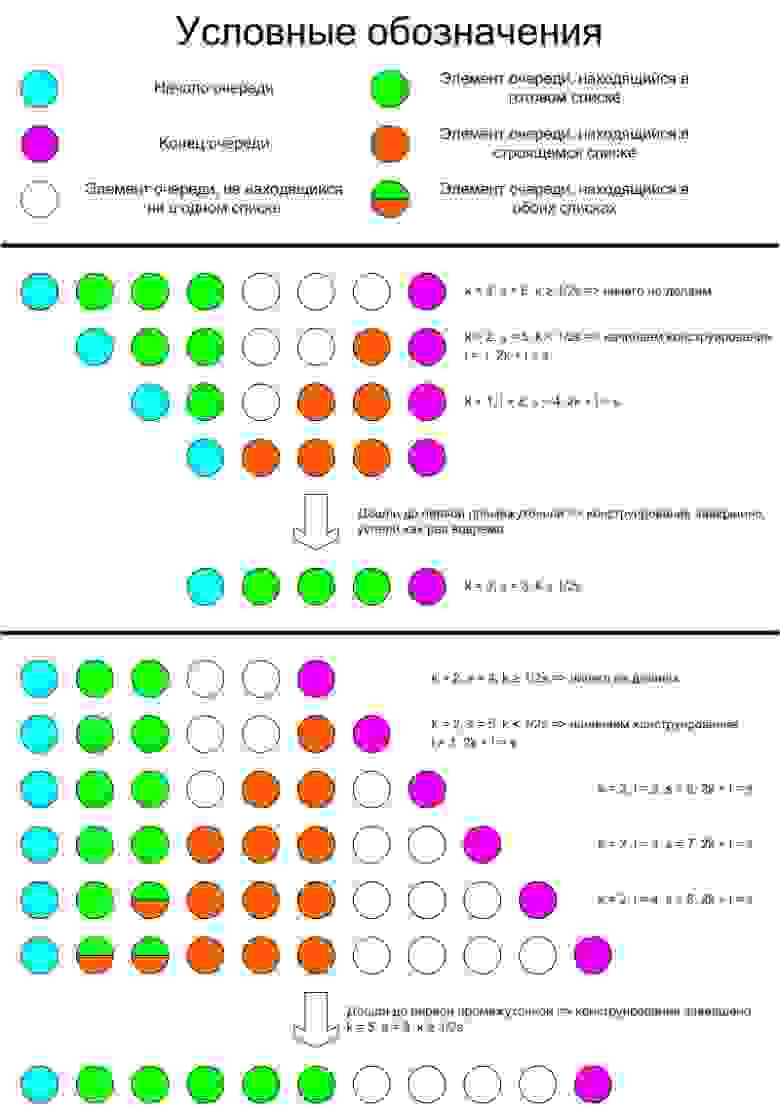
Напоследок приведу реализацию вышеописанной структуры данных на языке С++ (при реализации используются нововведения С++11). Стоит воспринимать этот код в качестве прототипа, я старался написать его как можно проще и короче, жертвуя всем остальным в угоду этому.
Типы TreeNode, Queue и QueueIntermediateTreeNodeList соотвествуют вершине дерева, очереди и элементу односвязного списка из нашего алгоритма. Булевы переменные в Queue используются для корректного освобождения памяти в деструкторе нашего класса: вершину дерева и элемент списка удаляет та очередь, которая их и создавала (как уже было отмечено выше, при каждом запросе создается не больше одной вершины и не больше одного элемента списка). Вершина дерева создается только при операции push и указатель на неё записывается в last, соответственно, own_last указывает, записана ли в last новая или старая вершина. Созданный же при конструировании элемент списка почти всегда записывается в constructing_intermediate_list, кроме случая, когда он был создан и конструирование на этом же шаге закончилось, в таком случае он переносится в known_intermediate_list, а constructing_intermediate_list становится нулем, и вторая булева переменная own_known_intermediate_list служит как раз для идентификации такого случая.
Второй возможно неочевидный момент — это закрытая функция-член manage_intermediate_lists, которая выглядит следующим образом:
Эта функция реализует вышеописанный алгоритм работы с указателем на строящийся список (обратите внимание, первые три параметра передаются по неконстантной ссылке, причем для первых двух предполагается, что переменные по ссылке инициализированы нужными значениями перед вызовом). Важно перед достройкой списка сначала проверять, а не стал ли старый элемент первым промежуточным, потому что, как уже отмечалось, в случае pop'а такой вариант возможен. Может быть кто-то заметил, что мы всегда проверяем на наш критерий начала конструирования:
Во-первых, как видно на схеме, при совершении нескольких различных операций c одной и той же очередью, для которой идет конструирование (на схеме это операции pop(Q) и push(Q, 11)), создается несколько абсолютно идентичных между собой элементов списка (они указывают на один и тот же следующий элемент и одну и ту же вершину дерева — на схеме это два голубых кружочка с цифрой 7). Мы могли бы попробовать «склеить» такие элементы в один, используя, например, структуру, которая при достраивании говорила бы нам, а не сделал ли уже это кто-то перед нами (в качестве такой структуры можно использовать банальный вектор или двусвязный список). Очевидно, такая оптимизация будет хорошо работать (экономить много памяти) в случае сильно разветвленных деревьев.
Во-вторых, у нас есть ещё одно дублирование: когда элементы готового и строящегося списка указывают на одну и ту же вершину дерева (речь идет о зелёно-оранжевых элементах на этой картинке). Конечно, полностью такого дублирования нам не избежать, потому что у списков вполне может быть одинаковое начало и отличающиеся друг от друга продолжения, однако мы могли бы, когда первый из строящихся списков достигнет конца готового (а не начала очереди) просто «подклеить» его к этому концу, тем самым сэкономив немножко памяти. Для оставшихся списков (соответствующих этому готовому, разумеется) все равно придется дублировать. Тем самым, данная оптимизация лучше всего будут себя проявлять, когда у нас на деревьях много длинных прямых веток.
Наконец в-третьих, можно попробовать поиграть с константами. Например, можно достраивать за шаг не по 1 элементу, а по 2, тогда начинать конструирование достаточно при k < 1/3s. Возможно, это будет как-то полезно.
На этом всё, спасибо всем, кто дочитал.
Постановка задачи
Реализовывать мы будем, естественно, так называемую полную персистентность — это значит, что промежуточные версии доступны не только в режиме read-only и мы можем в любой момент времени добавлять и извлекать из них элементы. Кроме того, нам, конечно, хотелось бы иметь такую же асимптотику времени работы и дополнительной памяти, как и для неперсистентного варианта, а именно O(n), где n — суммарное количество операций, совершаемых с нашей очередью. К слову, если ослабить требования до O(n log n), то очередь тривиально эмулируется с помощью персистентного декартового дерева по неявному ключу.
Примем следующий простой интерфейс работы с нашей структурой данных: получающиеся в результате запросов версии очередей будем нумеровать целыми неотрицательными числами, изначально имеется лишь пустая очередь под номером 0. Пусть у нас есть N версий очередей (включая исходную пустую), тогда они занумерованы числами от 0 до N-1 и мы можем выполнить следующие четыре запроса:
- empty(query_id) — проверяет пуста ли очередь c заданным номером;
- front(query_id) — возвращает первый элемент очереди, сама же очередь при этом никак не изменяется и никаких новых очередей не создается. Операция допустима, если очередь не пуста;
- push(query_id, new_element) — создает новую очередь под номером N, получающуюся дописыванием в конец к исходной нового элемента. Старая версия при этом по-прежнему доступна под номером query_id;
- pop(query_id) — создает новую очередь под номером N, получающуюся извлечением из исходной первого элемента. Исходная очередь все также доступна под старым номером. В случае, если исходная очередь была пуста, новая также будет пустой.
Имитация очереди с помощью стеков
For every problem there is a solution which is simple, fast, and wrong.
— The First Law of Online Judges
Как известно, персистентный стек — очень простая структура данных и асимптотика у него та, что нам и нужна. Кроме того, мы знаем, что очередь можно имитировать с помощью двух стеков. Возникает очевидная идея: сделаем эти два стека персистентными и задача решена! К сожалению, такой простой подход не сработает. Все дело в том, что при данной имитации у нас не всякая операция имеет асимптотику O(1): если при pop’е стек, из которого мы достаем элементы, оказывается пустым, то мы перекладываем в него все элементы из другого стека. В случае с обычным очередью каждый элемент перекладывается только один раз, поэтому суммарная асимптотика остается O(n), но в персистентном случае каждый элемент может принадлежать многим очередям и соответственно быть переложен несколько раз. Пусть, например, q — номер очереди, у которой этот стек пустой, тогда после push(q, 1) и push(q, 2) у полученных очередей этот стек останется пустым и при pop’е из них каждый элемент очереди q будет переложен по два раза. Организовать же какое-либо совместное использование переложенных элементов невозможно в силу того, что самые нижние элементы у полученных перекладыванием стеков будут различны (1 и 2 соотвественно), а персистентный стек устроен таким образом, что каждый элемент хранит указатель на элемент, лежащий ниже его, поэтому в любом случае мы будем вынуждены иметь 2 копии предпоследнего элемента, которые будут указывать на соответствующий последний, а значит и 2 копии предпредпоследнего, чтобы указывать на нужный предпоследний и так далее по цепочке.
Тем не менее существует алгоритм, основанный на такой идее (имитации очереди с помощью двух стеков), гарантирующий, что стек, из которого мы достаем при pop’e, никогда не окажется пустым и использующий для обеспечения этого 6 стеков. Мой же алгоритм эту идею в явном виде не использует, хотя при общие моменты, конечно, найти можно.
Описание алгоритма
Попытаемся использовать ту же структуру, что и при реализации персистентного стека: будем хранить добавляемые элементы в виде дерева (точнее говоря, набора деревьев — леса), в каждой вершине будет лежать добавленный элемент и указатель на предшествующий ему в очереди (точнее, на соответствующую этому предшествующему элементу вершину дерева). Говоря в дальнейшем элемент очереди, я часто буду подразумевать именно соответствующую элементу вершину.
Непустая очередь в таком случае может быть представлена парой указателей на первый и последний элемент очереди, причем вершина, соответствующая первому элементу, обязательно будет предком вершины, соответствующей последнему (ну или совпадать с ней в случае очереди из одного элемента). Пример такой структуры и отображения в ней очереди:
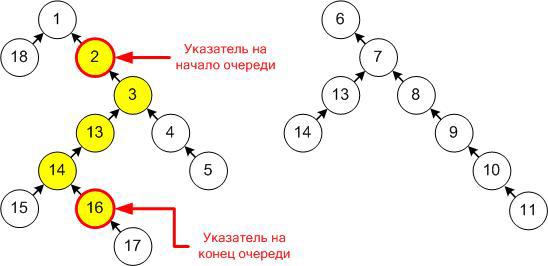
Заметим, что операция push просто создает новую вершину, устанавливая ей в качестве родителя последний элемент исходной очереди (либо она становится новым корнем, если добавляли в пустую), а операция pop наш лес вообще не трогает, просто сдвигает указатель на первый элемент. Тем самым, после создания вершина остается неизменной до конца работы и можно не переживать, что новые операции могут каким-либо образом испортить уже существующие очереди.
Наша единственная проблема при таком подходе – это реализация операции pop (остальные три — тривиальны), непонятно, как определить на какую вершину сдвинуть указатель на первый элемент, ведь для вершины мы храним лишь указатель на родителя, но не на сыновей (коих у одной вершины может быть несколько штук, и, даже если их все хранить, совершенно неясно, какой из них соответствует следующему элементу нашей очереди). Поэтому для каждой очереди, в которой больше двух элементов, будем дополнительно хранить указатель на элемент некоторого односвязного списка, такого, что элемент списка по нашему указателю содержит указатель на второй элемент нашей очереди, а элементы, лежащие ниже его по списку, указатели на третий, четвертый и так далее соответственно. Имея такой указатель для исходной очереди, при выполнении pop'а нам не составит теперь труда определить новую голову очереди, а указатель на такой элемент списка для получившейся очереди – это просто указатель на следующий элемент в данном списке.
Однако, по причинам, аналогичным тем, по которым эмуляция очереди двумя стеками не работает, добиться того, чтобы для каждой очереди ниже по списку лежали абсолютно все её промежуточные вершины, у нас не выйдет, поэтому, пускай, в нем будут лежать только сколько-то первых из них, а мы, когда этот список начнет становиться слишком маленьким, будем строить новый список, продвигаясь шаг за шагом (то есть увеличивая строящийся список на 1 элемент с каждой операцией push или pop) с конца очереди в начало, идя по указателям на родителей вершин нашего дерева и стараясь, чтобы к моменту, когда старый список закончится, у нас уже был новый наготове.
Говоря более формально, для каждой очереди помимо указателей на начало и конец и указателя на элемент уже готового списка будем хранить ещё и указатель на элемент строящегося списка (в случае, если мы ничего не строим, он будет равен 0) и вычислять его значение для новой очереди (полученной после применения к исходной push’a или pop’a) по следующему простому алгоритму:
- если у исходной очереди данный указатель был равен 0, проверим, не пора ли нам начать строить новый список (критерий такой проверки будет описан чуть ниже):
- если пора, то создаем элемент списка с нулевым указателем на следующий по списку (тем самым этот созданный элемент будет концом конструируемого списка), а указатель на вершину ставим на предпоследний элемент нашей очереди (родителя последнего элемента),
- если ещё не время, то указатель оставляем равным нулю.
- В случае же ненулевого исходного указателя, достроим наш список вверх на один элемент: создадим новый элемент, указывающий на исходный в качестве следующего по списку и на родителя соответствующей этому исходному элементу вершины.
При этом ни сам исходный элемент списка, ни указатель на него, хранящийся для исходной очереди, мы менять не будем, и вообще, у нас все данные (вершины дерева, элементы списков, данные, хранящиеся для очередей) будут иммутабельны (то есть после создания никогда не будут менять своего значения). Изображение того, как это всё устроено и что происходит при push’e или pop’e, можно увидеть на схеме (сделать её более понятной не получилось, сколько ни старался):
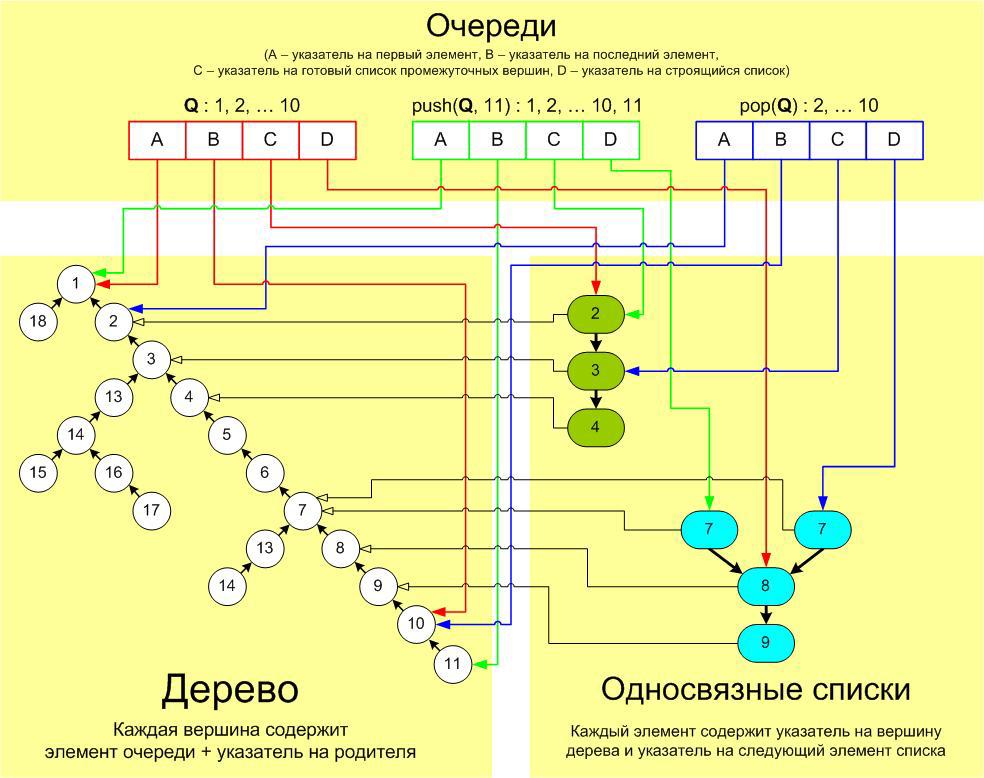
Соответственно, если при достройке списка мы доходим до первого промежуточного элемента, то конструирование для этой очереди завершено (при этом какие-то другие очереди могут продолжать достраивать этот список, но так как старые элементы никогда не меняются, нам это никак не навредит). В таком случае на место указателя на элемент старого списка записываем указатель на элемент нового, а указатель на конструируемый список присваиваем нулю.
Из описания алгоритма видно, что при выполнении каждого запроса мы создаем не более одной новой вершины дерева и не более одного нового элемента списка и тратим на выполнение O(1) времени, то есть асимптотика та, которой мы и добивались, и осталось лишь обсудить правильный критерий.
Критерий проверки на начало конструирования
Будем действовать следующим образом: пока размер нашего списка больше либо равен 1/2 от количества промежуточных вершин (то есть вершин без первой и последней), мы ничего не предпринимаем, как только станет меньше, начинаем конструировать новый. Заметим, что если промежуточных вершин нет, то мы имеем неравенство 0 ≥ 0 и ничего не делаем, то есть в особый случай это выделять не нужно. Докажем, что при таком подходе мы никогда не окажемся в ситуации, когда старый список кончился, а новый ещё не готов.
Для начала докажем следующий инвариант: если мы конструируем новый список, то на каждом шаге 2k + l = s, где k — количество элементов в старом списке, l — в конструируемом (после уже выполненной на этом шагу достройки), s — суммарное количество промежуточных элементов. Доказывать будем методом математической индукции. Рассмотрим первый шаг, когда мы только начали конструирование (l = 1). Заметим, что для новой очереди 2k – s < 0 (наш критерий), однако для исходной 2kold – sold ≥ 0. Посмотрим, как такое могло случиться: если наша операция push, то k = kold, а s = sold + 1, а если pop, то k = kold – 1 и s = sold – 1. Как нетрудно заметить, в обоих случаях 2k – s меньше 2kold – sold ровно на единицу и, так как обе разности — целые числа, значит, вторая из них 0, а первая -1, следовательно, 2k + 1 = s, а наше l как раз единица и есть. База индукции доказана. Докажем переход: пусть на каком-то шаге конструирования 2kold + lold = sold. Тогда l = lold + 1 (достроили список на 1 элемент), в случае push’a: k = kold, s = sold + 1, в случае pop’a: k = kold – 1, s = sold – 1. В обоих случаях равенство выполняется, а значит утверждение доказано.
Предположим теперь, что мы делаем операцию pop, а у исходной очереди нужный нам список пустой (при push’е мы этот список никак не используем). Тогда может быть одно из двух:
- либо для исходной очереди мы конструирование нового списка не начинали, тогда у этой очереди 2k ≥ s,
k = 0 => s = 0, а значит, это очередь размером 0, 1 или 2 и знания её последнего элемента для совершения pop’a достаточно, - либо начинали, тогда l ≠ 0, в силу инварианта 2k + l = s, k = 0 => l = s ≠ 0 => конструируемый список был непуст и содержал все промежуточные элементы, а значит, мы должны были произвести на том шаге замену и получить непустой список.
Осталось лишь доказать, что, когда мы заканчиваем конструирование, условие отсутствия конструирования выполняется, то есть длина получившегося списка не меньше 1/2 от общего количества промежуточных вершин, иными словами, что в момент завершения 2l ≥ s или, что равносильно, l ≥ s – l. Но что такое s – l? Это количество промежуточных вершин, которые не содержатся в нашем списке. Нетрудно понять, что оно равно количеству операций push, произошедших в процессе конструирования. Однако при каждой такой операции количество элементов в нашем списке также увеличивалось на 1 (возможна ситуация, когда на предыдущем шаге элемент конструируемого списка соответствует третьему по счету элементу очереди и мы делаем pop, тогда для новой очереди элемент списка начинает соответствовать первому промежуточному элементу сразу без достройки, но такое возможно только на последнем шаге конструирования и только при операции pop). Поэтому l ≥ количества таких push’ей (не трудно понять, что даже строго больше), что нам и требовалось доказать.
Для наглядности, продемонстрируем, что происходит в двух крайних случаях: когда мы все время выполняем pop и когда все время push'им:
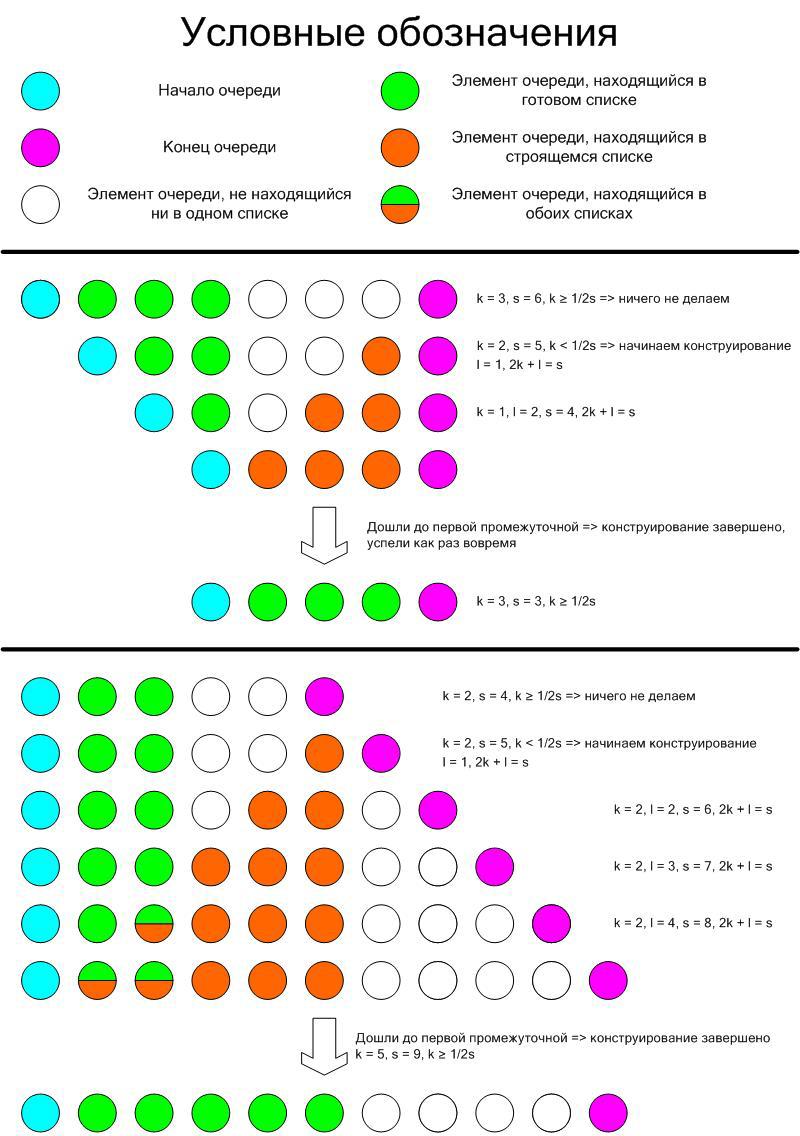
Реализация на С++
Напоследок приведу реализацию вышеописанной структуры данных на языке С++ (при реализации используются нововведения С++11). Стоит воспринимать этот код в качестве прототипа, я старался написать его как можно проще и короче, жертвуя всем остальным в угоду этому.
persistent_queue.h
#ifndef PERSISTENT_QUEUE_H
#define PERSISTENT_QUEUE_H
#include <cstdlib>
#include <vector>
using Element_type = int;
class Persistent_queue {
public:
Persistent_queue();
~Persistent_queue();
Persistent_queue(const Persistent_queue&) = delete;
Persistent_queue& operator =(const Persistent_queue&) = delete;
using Queue_id = size_t;
static const Queue_id start_queue_id = 0;
Queue_id push(Queue_id queue_id, const Element_type& value);
Queue_id pop(Queue_id queue_id);
const Element_type& front(Queue_id queue_id);
size_t size(Queue_id queue_id);
bool empty(Queue_id queue_id);
private:
struct TreeNode;
struct QueueIntermediateTreeNodeList;
struct Queue {
const TreeNode* const first;
const TreeNode* const last;
const size_t size;
const QueueIntermediateTreeNodeList* const known_intermediate_list;
const QueueIntermediateTreeNodeList* const constructing_intermediate_list;
const bool own_last;
const bool own_known_intermediate_list;
Queue(const TreeNode* const first, const TreeNode* const last, const size_t size,
const QueueIntermediateTreeNodeList* const known_intermediate_list,
const QueueIntermediateTreeNodeList* const constructing_intermediate_list,
const bool own_last, const bool own_known_intermediate_list);
~Queue() = default;
Queue(Queue&& source) = default; // needed for vector reallocation
Queue(const Queue&) = delete;
Queue& operator =(const Queue&) = delete;
};
std::vector<Queue> queues_;
Queue_id register_new_queue(const TreeNode* const first, const TreeNode* const last,
const size_t size,
const QueueIntermediateTreeNodeList* const known_intermediate_list,
const QueueIntermediateTreeNodeList* const constructing_intermediate_list,
const bool own_last, const bool own_known_intermediate_list);
void manage_intermediate_lists(const QueueIntermediateTreeNodeList*& known_intermediate_list,
const QueueIntermediateTreeNodeList*& constructing_intermediate_list,
bool& own_known_intermediate_list, const TreeNode* const first, const TreeNode* const last,
const size_t size);
};
#endif // PERSISTENT_QUEUE_H
persistent_queue.cpp
#include "persistent_queue.h"
#include <cassert>
struct Persistent_queue::TreeNode {
const TreeNode* const parent;
const Element_type element;
TreeNode(const TreeNode* const parent, const Element_type& value)
: parent(parent), element(value) {}
~TreeNode() = default;
TreeNode(const TreeNode&) = delete;
TreeNode& operator =(const TreeNode&) = delete;
};
struct Persistent_queue::QueueIntermediateTreeNodeList {
const Persistent_queue::TreeNode* const front;
const QueueIntermediateTreeNodeList* const next;
const size_t size;
QueueIntermediateTreeNodeList(const Persistent_queue::TreeNode* const front,
const QueueIntermediateTreeNodeList* const tail_list)
: front(front), next(tail_list), size{tail_list ? tail_list->size + 1 : 1} { assert(front); }
~QueueIntermediateTreeNodeList() = default;
QueueIntermediateTreeNodeList(const QueueIntermediateTreeNodeList&) = delete;
QueueIntermediateTreeNodeList& operator =(const QueueIntermediateTreeNodeList&) = delete;
};
Persistent_queue::Queue::Queue(
const Persistent_queue::TreeNode* const first, const Persistent_queue::TreeNode* const last,
const size_t size, const Persistent_queue::QueueIntermediateTreeNodeList* const known_intermediate_list,
const Persistent_queue::QueueIntermediateTreeNodeList* const constructing_intermediate_list,
const bool own_last, const bool own_known_intermediate_list
)
: first(first), last(last), size(size), known_intermediate_list(known_intermediate_list)
, constructing_intermediate_list(constructing_intermediate_list)
, own_last(own_last), own_known_intermediate_list(own_known_intermediate_list)
{
// Some asserts
if (size == 0) {
assert(first == nullptr);
assert(last == nullptr);
} else {
assert(first);
assert(last);
if (size > 1)
assert(last->parent);
}
if (size <= 2) {
assert(known_intermediate_list == nullptr);
assert(constructing_intermediate_list == nullptr);
if (size == 1)
assert(first == last);
if (size == 2)
assert(first == last->parent);
} else {
assert(known_intermediate_list);
assert(first == known_intermediate_list->front->parent);
}
}
size_t Persistent_queue::size(const Persistent_queue::Queue_id queue_id)
{
return queues_.at(queue_id).size;
}
bool Persistent_queue::empty(const Queue_id queue_id)
{
return size(queue_id) == 0;
}
const Element_type& Persistent_queue::front(const Persistent_queue::Queue_id queue_id)
{
assert(!empty(queue_id));
return queues_.at(queue_id).first->element;
}
Persistent_queue::Queue_id
Persistent_queue::register_new_queue(const TreeNode* const first, const TreeNode* const last,
const size_t size, const QueueIntermediateTreeNodeList* const known_intermediate_list,
const QueueIntermediateTreeNodeList* const constructing_intermediate_list,
const bool own_last, const bool own_known_intermediate_list)
{
queues_.emplace_back(first, last, size, known_intermediate_list, constructing_intermediate_list,
own_last, own_known_intermediate_list);
return queues_.size() - 1;
}
Persistent_queue::Persistent_queue()
{
register_new_queue(nullptr, nullptr, 0, nullptr, nullptr, false, false);
}
Persistent_queue::~Persistent_queue()
{
for (const auto& q : queues_) {
if (q.own_last)
delete q.last;
if (q.own_known_intermediate_list)
delete q.known_intermediate_list;
delete q.constructing_intermediate_list;
}
}
Persistent_queue::Queue_id
Persistent_queue::push(const Persistent_queue::Queue_id queue_id, const Element_type& value)
{
const auto& queue_for_push = queues_.at(queue_id);
const size_t size = queue_for_push.size + 1;
const bool own_last = true;
const TreeNode* first;
const TreeNode* last;
if (queue_for_push.size == 0) {
first = last = new TreeNode(nullptr, value);
} else {
first = queue_for_push.first;
last = new TreeNode(queue_for_push.last, value);
}
bool own_known_intermediate_list;
const QueueIntermediateTreeNodeList* known_intermediate_list = queue_for_push.known_intermediate_list;
const QueueIntermediateTreeNodeList* constructing_intermediate_list =
queue_for_push.constructing_intermediate_list;
manage_intermediate_lists(known_intermediate_list, constructing_intermediate_list,
own_known_intermediate_list, first, last, size);
return register_new_queue(first, last, size, known_intermediate_list, constructing_intermediate_list,
own_last, own_known_intermediate_list);
}
Persistent_queue::Queue_id Persistent_queue::pop(const Persistent_queue::Queue_id queue_id)
{
const auto& queue_for_pop = queues_.at(queue_id);
const bool own_last = false;
const TreeNode* first;
const TreeNode* last;
size_t size;
const QueueIntermediateTreeNodeList* known_intermediate_list;
if (queue_for_pop.size <= 1) {
first = last = nullptr;
size = 0;
known_intermediate_list = nullptr;
} else {
last = queue_for_pop.last;
size = queue_for_pop.size - 1;
if (queue_for_pop.size == 2) {
first = queue_for_pop.last;
known_intermediate_list = nullptr;
} else {
assert(queue_for_pop.known_intermediate_list != nullptr);
first = queue_for_pop.known_intermediate_list->front;
known_intermediate_list = queue_for_pop.known_intermediate_list->next;
}
}
bool own_known_intermediate_list;
const QueueIntermediateTreeNodeList* constructing_intermediate_list =
queue_for_pop.constructing_intermediate_list;
manage_intermediate_lists(known_intermediate_list, constructing_intermediate_list,
own_known_intermediate_list, first, last, size);
return register_new_queue(first, last, size, known_intermediate_list, constructing_intermediate_list,
own_last, own_known_intermediate_list);
}
void Persistent_queue::manage_intermediate_lists(
const Persistent_queue::QueueIntermediateTreeNodeList*& known_intermediate_list,
const Persistent_queue::QueueIntermediateTreeNodeList*& constructing_intermediate_list,
bool& own_known_intermediate_list, const Persistent_queue::TreeNode* const first,
const Persistent_queue::TreeNode* const last, const size_t size)
{
own_known_intermediate_list = false;
const size_t intermediate_nodes_count = (size > 2 ? size - 2 : 0);
size_t known_intermediate_list_size =
(known_intermediate_list ? known_intermediate_list->size : 0);
if (2*known_intermediate_list_size < intermediate_nodes_count) {
auto try_to_replace_known_to_constructing = [&](){
if (constructing_intermediate_list && constructing_intermediate_list->front->parent == first) {
known_intermediate_list = constructing_intermediate_list;
known_intermediate_list_size = constructing_intermediate_list->size;
constructing_intermediate_list = nullptr;
return true;
}
return false;
};
if (!try_to_replace_known_to_constructing()) {
const auto adding_node = (constructing_intermediate_list ?
constructing_intermediate_list->front->parent : last->parent);
constructing_intermediate_list = new QueueIntermediateTreeNodeList(
adding_node, constructing_intermediate_list);
if (try_to_replace_known_to_constructing())
own_known_intermediate_list = true;
}
}
// Check invariants
if (2*known_intermediate_list_size >= intermediate_nodes_count)
assert(constructing_intermediate_list == nullptr);
const size_t constructing_intermediate_list_size =
(constructing_intermediate_list ? constructing_intermediate_list->size : 0);
const auto invariant_sum = 2*known_intermediate_list_size + constructing_intermediate_list_size;
assert(invariant_sum >= intermediate_nodes_count);
if (constructing_intermediate_list)
assert(invariant_sum == intermediate_nodes_count);
}
Типы TreeNode, Queue и QueueIntermediateTreeNodeList соотвествуют вершине дерева, очереди и элементу односвязного списка из нашего алгоритма. Булевы переменные в Queue используются для корректного освобождения памяти в деструкторе нашего класса: вершину дерева и элемент списка удаляет та очередь, которая их и создавала (как уже было отмечено выше, при каждом запросе создается не больше одной вершины и не больше одного элемента списка). Вершина дерева создается только при операции push и указатель на неё записывается в last, соответственно, own_last указывает, записана ли в last новая или старая вершина. Созданный же при конструировании элемент списка почти всегда записывается в constructing_intermediate_list, кроме случая, когда он был создан и конструирование на этом же шаге закончилось, в таком случае он переносится в known_intermediate_list, а constructing_intermediate_list становится нулем, и вторая булева переменная own_known_intermediate_list служит как раз для идентификации такого случая.
Второй возможно неочевидный момент — это закрытая функция-член manage_intermediate_lists, которая выглядит следующим образом:
void Persistent_queue::manage_intermediate_lists(
const Persistent_queue::QueueIntermediateTreeNodeList*& known_intermediate_list,
const Persistent_queue::QueueIntermediateTreeNodeList*& constructing_intermediate_list,
bool& own_known_intermediate_list, const Persistent_queue::TreeNode* const first,
const Persistent_queue::TreeNode* const last, const size_t size)
{
own_known_intermediate_list = false;
const size_t intermediate_nodes_count = (size > 2 ? size - 2 : 0);
size_t known_intermediate_list_size =
(known_intermediate_list ? known_intermediate_list->size : 0);
if (2*known_intermediate_list_size < intermediate_nodes_count) {
auto try_to_replace_known_to_constructing = [&](){
if (constructing_intermediate_list && constructing_intermediate_list->front->parent == first) {
known_intermediate_list = constructing_intermediate_list;
known_intermediate_list_size = constructing_intermediate_list->size;
constructing_intermediate_list = nullptr;
return true;
}
return false;
};
if (!try_to_replace_known_to_constructing()) {
const auto adding_node = (constructing_intermediate_list ?
constructing_intermediate_list->front->parent : last->parent);
constructing_intermediate_list = new QueueIntermediateTreeNodeList(
adding_node, constructing_intermediate_list);
if (try_to_replace_known_to_constructing())
own_known_intermediate_list = true;
}
}
// Check invariants
}
Эта функция реализует вышеописанный алгоритм работы с указателем на строящийся список (обратите внимание, первые три параметра передаются по неконстантной ссылке, причем для первых двух предполагается, что переменные по ссылке инициализированы нужными значениями перед вызовом). Важно перед достройкой списка сначала проверять, а не стал ли старый элемент первым промежуточным, потому что, как уже отмечалось, в случае pop'а такой вариант возможен. Может быть кто-то заметил, что мы всегда проверяем на наш критерий начала конструирования:
if (2*known_intermediate_list_size < intermediate_nodes_count) {Возможные оптимизации
Во-первых, как видно на схеме, при совершении нескольких различных операций c одной и той же очередью, для которой идет конструирование (на схеме это операции pop(Q) и push(Q, 11)), создается несколько абсолютно идентичных между собой элементов списка (они указывают на один и тот же следующий элемент и одну и ту же вершину дерева — на схеме это два голубых кружочка с цифрой 7). Мы могли бы попробовать «склеить» такие элементы в один, используя, например, структуру, которая при достраивании говорила бы нам, а не сделал ли уже это кто-то перед нами (в качестве такой структуры можно использовать банальный вектор или двусвязный список). Очевидно, такая оптимизация будет хорошо работать (экономить много памяти) в случае сильно разветвленных деревьев.
Во-вторых, у нас есть ещё одно дублирование: когда элементы готового и строящегося списка указывают на одну и ту же вершину дерева (речь идет о зелёно-оранжевых элементах на этой картинке). Конечно, полностью такого дублирования нам не избежать, потому что у списков вполне может быть одинаковое начало и отличающиеся друг от друга продолжения, однако мы могли бы, когда первый из строящихся списков достигнет конца готового (а не начала очереди) просто «подклеить» его к этому концу, тем самым сэкономив немножко памяти. Для оставшихся списков (соответствующих этому готовому, разумеется) все равно придется дублировать. Тем самым, данная оптимизация лучше всего будут себя проявлять, когда у нас на деревьях много длинных прямых веток.
Наконец в-третьих, можно попробовать поиграть с константами. Например, можно достраивать за шаг не по 1 элементу, а по 2, тогда начинать конструирование достаточно при k < 1/3s. Возможно, это будет как-то полезно.
На этом всё, спасибо всем, кто дочитал.