Проблема факторизации составных натуральных чисел (сннч) многие столетия удерживает внимание специалистов в различных теоретических (научных) и прикладных областях таких как числовые системы, вычислительная математика и техника, теория чисел, информационная безопасность, криптография, и др., и вынуждает их прикладывать немалые усилия к ее положительному и успешному решению. Тем не менее, проблема и сегодня далека от ее закрытия, завершения. Автор предлагает к рассмотрению и стремится дать читателю понятие о существующих подходах к решению проблемы, ставших уже своеобразной классикой, привести критику и выразить одобрение замечательным находкам.
В работе излагается один из известных подходов к решению задачи факторизации больших чисел (ЗФБЧ), использующий математику эллиптических кривых (ЭК). Об этой математике, а точнее о технике вычислений приведу цитату авторов из [ 1 ] «Техника, используемая в настоящее время при изучении ЭК, является одной из самых изощренных во всей математике. Мы надеемся, что элементарный подход настоящей работы побудит читателя к дальнейшему изучению этой живой и пленительной ветви теории чисел. Есть много того, что следует изучить, и много работы, которую еще надо проделать. „
Удобно теоретическое изложение материала построить в сопровождении конечного числового примера и детальных отступлений и комментариев, что позволит, не перескакивая по разным частям работы, и успешней вникать в существо излагаемого материала. Понятно, что задача не из простых и требует от читателя определенной предварительной подготовки, но такова специфика “Хабра» — наличие читателей разного уровня подготовки.
Вначале приведем несколько необходимых определений высшей алгебры.
Алгебраической (конечной) группой называется множество элементов (чисел, многочленов, матриц и др.) над которыми задана одна операция. В зависимости от природы элементов (матрицы, подстановки, вычеты по модулю N) операции могут различаться, но названия их, как правило, всегда одинаковы: сложение и умножение. В случае групп вычетов по модулю N множество элементов группы может быть целыми или даже натуральными пополненными нулем числами от 0 до N — 1. Единственная операция группы по назначению может быть сложением (+), и тогда группа называется аддитивной, или умножением (•), и группа называется мультипликативной. Обеим операциям групп присущи близкие свойства (описываемые развернуто в учебной литературе): ассоциативность, замкнутость, наличие нейтрального и противоположного (обратного) элементов, а при сохранении результата операции в случае смены операндов местами — коммутативность. Поясним свойство замкнутости. Множество элементов, образующих конечную группу, конечно и постоянно. Результатами операции всегда являются элементы из исходного множества. Среди элементов группы только один — нейтральный элемент, и каждый элемент имеет себе обратный (а-1) (или противоположный (-а)). Операция над элементами не выводит результат за пределы исходного множества элементов группы. Дело в том, что в группах вычетов по модулю N операции сложение или умножение не обычные, а модулярные, т. е. для группы задается число N, называемое модулем группы, и на него делятся все получаемые результаты. Такое деление, как правило, выполняется с остатком и именно остаток принимается за окончательный результат операции.
Математик Кэли предложил характеризовать множество результатов таких операций таблицами, которые получили его имя (таблицы Кэли), таблицей сложения для аддитивной группы и таблицей умножения — для мультипликативной.
Порядок группы — число ее элементов. Каждый отдельный элемент в группе также характеризуется его порядком.
Порядок (период) элемента в группе — это наименьшее положительное число (кратность k элемента) в операции, при котором результат операции обращается в нейтральный элемент.
а+а +...+а = ka = 0 или a∙a∙a∙...∙a = ak = 1.
Период элемента кратен порядку группы, т.е. делит нацело порядок группы.
Алгебраическим числовым конечным простым полем вычетов по простому модулю N называется множество (k, GF(p), Fp) элементов (чисел от 0 до N — 1), над которыми заданы две операции сложение (+) и умножение (•). Модуль N, по которому формируются элементы поля, должен быть обязательно простым числом. Среди элементов обязательно имеются противоположные (-а) к каждому элементу и один нейтральный (0) по сложению, обратные (а-1) к каждому элементу и один нейтральный (1) по умножению. Поле образовано в соответствии с операциями допустимыми в нем (+) и (•) двумя соответствующими группами.
Кроме конечных числовых простых полей в различных теориях (кодирования, криптографии, алгебре, геометрии и т.п.) используются поля многочленов.
Такие поля GF(pn) появляются как результат расширения определенной степени n простых полей GF(p).
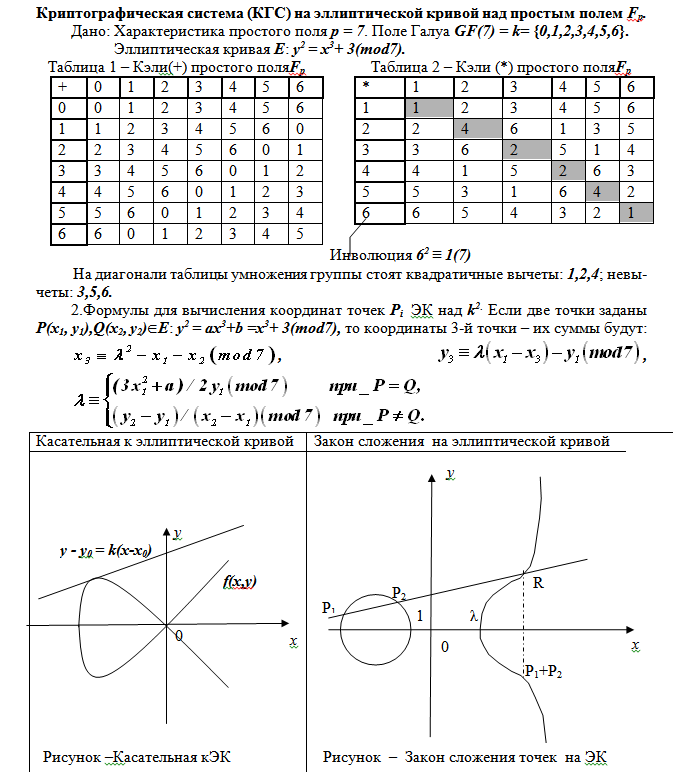
Расширение поля — поле GF(pn), содержащее данное поле GF(p) в качестве подполя, что записывают так К/k, где k = GF(p), К=GF(pn) — расширение поля k. Элементами поля расширения K являются все элементы (числа) простого поля k и все многочлены степени не превышающей n — 1. Иллюстрацией групп поля и результатов обеих операций в группах для примера поля GF(7) сложения и умножения являются числовые таблицы 1 и 2 помещенные ниже
Алгебраическим числовым конечным кольцом вычетов по модулю N (обозначается ZN) называется множество элементов (чисел от 0 до N — 1), над которыми заданы две операции сложение (+) и умножение (•). Модуль N, по которому формируются элементы кольца должен быть составным (не простым) числом. Если модуль сделать простым числом ( неприводимым многочленом ), то кольцо преобразуется в простое поле ( поле многочленов ). Среди элементов кольца обязательно имеются противоположные (-а) к каждому элементу и нейтральный (0) по сложению, но обратный элемент (а-1) существует не для каждого элемента и нейтральный элемент (1) по умножению в кольце может отсутствовать. Если модулем приведения является приводимый многочлен степени n, то возникает кольцо многочленов, элементами которого являются фактически те же самые элементы, что и в поле многочленов, но операции над многочленами выполняются уже не так как в поле расширения. Аналогичная ситуация с элементами возникает и для векторных пространств — они там такие же как в поле и в кольце. Операции же существенно различны. Результаты операции умножения элементов поля и тех же элементов кольца или векторного пространства будут различаться. Для нашего изложения существенно то, что не все элементы имеют обратные в мультипликативной группе кольца.
Пример 1. Пусть задано простое поле вычетов по модулю два — двоичное поле GF(2) = {0,1}. Построим поле расширения степени, например, n = 6, что обозначается так GF(26 ). Это поле образуют числа 0, 1 и все возможные многочлены степени не превышающей 5. Когда выполняются действия с многочленами в мультипликативной группе поля, то степень результата (произведения многочленов) degd(x) может превышать показатель степени n = 5. При этом условие замкнутости множества элементов мультипликативной группы нарушается. Чтобы вернуть результат в поле — сделать его элементом поля, результат произведения делят на специально выбираемый многочлен ( например, f(х) = х6 + х + 1) степени равной степени расширения, т.е. n = 6. Такой многочлен в сущности формирует поле и не должен иметь корней в простом поле, он называется неприводимым многочленом, т. е. он не раскладывается на сомножители в поле.
Говорят результаты операций поля приводятся по модулю неприводимого многочлена. Кроме того, все коэффициенты многочленов в поле принадлежат простому полю и приводятся по модулю простого поля (простого числа). Таким образом, результаты операций в поле приводятся по двойному модулю, что иногда обозначается так d(х)(moddp,f(x)), где р — простое число, формирующее простое поле, а f(x) — неприводимый многочлен степени равной степени расширения простого поля.
ЭЛЕМЕНТЫ ТЕОРИИ ЭЛЛИПТИЧЕСКОЙ КРИВОЙ
Моделирование многих явлений действительности, в частности, математических удобно выполнять с привлечением алгебраических структур: групп, полей, колец, алгебр и др. Те свойства, которые уже хорошо изучены для определенных структур, наследуются объектами, которые моделируются с использованием таких структур. Тем самым экономятся время и силы, а также и другие ресурсы. Одним из примеров использования известных свойств конечных аддитивных групп является разработка алгоритмов решения ЗФБЧ, алгоритмов цифровой подписи и/или шифрования документов (сообщений), в которых привлекаются не совсем обычные группы. В алгоритмах используются точки алгебраической кривой, заданной над конечными структурами (поле, кольцо), редуцированной (вычисления приводятся по модулю характеристики N) называемой эллиптическая кривая (ЭК) в форме Вейерштрасса, целочисленные (рациональные) точки которой образуют аддитивную группу, т. е. их можно суммировать в любом порядке, получая при этом новые точки из этой группы. При определенных условиях, накладываемых на кривую, множество таких точек замкнуто и конечно, хотя порядок группы может быть очень большим. Сама кривая плоская ее коэффициенты а и b; точки ЭК (х, у) описываются через две х и у переменные, значения которых принадлежат конечному простому полю Галуа GF(p) (но могут принадлежать и расширенному полю GF(pn), как в некоторых стандартах электронной цифровой подписи (ЭЦП)), таким образом, в алгоритмах используется декартово произведение поля GF(p)хGF(p).
Операция сложения точек ЭК — это специальная операция (+), заключительный шаг которой взятие результата по модулю N простому или (для кольца) составному. При составном модуле ЭК задана не над полем, а над кольцом, что существенно изменяет свойства рассматриваемых объектов, сохраняя основные из них.
Рассмотрим самые начальные сведения из теории и арифметики эллиптических кривых. Необходимо уяснить ряд моментов. Задание ЭК, смысловое значение параметров ЭК, множество целых точек и возможность их сложения между собой. Операция сложения точек. Эти сведения и их понимание необходимы для доступного изложения алгоритма факторизации натуральных (целых) чисел, который давно известен специалистам-криптологам по публикациям Х. Ленстра от 1987 г и более поздним усовершенствованиям Р. Монтгомери 1992 [2, 4, 5, 6, 7,10 ]. Для задания эллиптической кривой Еa,b(Fр) над полем вначале задается поле характеристикой конечного поля — простым числом N или p>3. Для задания коэффициентов а и b эллиптической кривой Е (а, b), определенной над конечным простым полем Fр, можно воспользоваться подходом из отечественного стандарта. (ГОСТ).
Таким образом, эллиптической кривой Еa,b(Fр) называется множество {(х, у)} пар чисел, элементов поля х, у∊Fр, удовлетворяющих соотношению у2 ≡ х3+ах +b(modp), где а, b∊Fр. У Еa,b(Fр) дискриминант равен -4а3 + 27b2 ≢ 0(modp) и не сравним с нулем по модулю р. Правильнее сказать так называется группа точек ЭК, а не сама кривая. Но такая замена понятий в чем-то упрощает изложение.
Коэффициенты ЭК а, b определяются соотношениями а ≡ 3k(modp); b ≡ 3k(modp);
где k ≡ J(E)(1728 — J(E))-1(modp); J(E) ≡1728∙4а3(4а3+27b2)-1(modp) инвариант ЭК; J(E) ≠ 0∨1728.
Пары чисел (х, у), удовлетворяющие уравнению ЭК, называются ее точками, обозначаемыми Q(х, у), а х и у — координатами точки. В группу точек ЭК в качестве нейтрального элемента включается специальная точка (О) — точка удаленная в бесконечность (∞ ), ее координаты обычно не вычисляются. На множестве всех целых точек ЭК вводится операция сложения (+). Для двух произвольных точек Q1(х1, у1) и Q2(х2, у2) кривой Е(а,b) суммирование выполняется по различающимся формулам в зависимости от соотношения координат точек.
При равенстве обеих координат у точек х1= х2, у1= у2≠ 0 имеем удвоение или сумму одной точки с собой. Результирующая точка Q3(х3, у3) получает координаты, вычисляемые по формулам
х3 ≡ λ2 — 2х1(modp);
у3 ≡ λ(х1 — х3) — у1(modp),
где λ ≡ (3х12 + а)(2у1)-1(modp).
При х1 ≠ х2 суммой точек Q1(х1, у1) и Q2(х2, у2) является точка Q3(х3, у3), которая получает координаты, вычисляемые по формулам
х3 ≡ λ2 — х1 — х2(modp);
у3 ≡ λ(х1-х3) — у1(modp),
где λ ≡ (у2 — у1)(х2 — х1)-1(modp).
При х1= х2, у2= — у1(modp), точки лежат на вертикальной прямой, пересекающей в них ЭК.Эта прямая пересекает и третью точку (О) ЭК, которая удалена в бесконечности. Сумма точек Q1(х1, у1) и Q2(х2, у2) называется нейтральным элементом (нулевой точкой O) группы, координаты которой не определяются. Суммирование с этой точкой любой другой точки не изменяет эту другую и дает результат Q + О = О + Q = Q.
Точка Q имеет кратность k или называется просто кратной точкой Е(а, b), если для некоторой точки Р∊Е(а, b) выполнено равенство Q = Р + Р + ...+ Р = kP. Если для точки Р выполнено Р + Р + ...+ Р = kP = О, то k — порядок точки Р.
Операция суммирования всех целых точек Е(а,b) вместе с нулевой точкой О (нейтральный элемент) порождает конечную (коммутативную) аддитивную (абелеву) группу порядка q, где q ≠ p. Для этого порядка справедливо установленное Хассе соотношение р + 1 — 2√р < q < р + 1 + 2√р.
ПРОСТАЯ КРИПТОГРАФИЧЕСКАЯ СИСТЕМА НА ЭЛЛИПТИЧЕСКИХ КРИВЫХ
В сети обмена данными для всех абонентов задается общая редуцированная эллиптическая кривая Еa,b(Fр) над полем Fр и порождающая точка Р = (х, у) на ней. Каждый абонент, используя точки аддитивной группы этой ЭК формирует свои открытый и закрытый ключи. Ниже в примере 2 рассматривается простой вариант криптографической системы (КГС) с возможностью шифрования/расшифрования сообщений элементами группы точек ЭК. Понимание основ теории эллиптических кривых и смежных вопросов открывает возможности использование богатого арсенала их средств в целях повышения уровня безопасности информационных систем и предотвращения возможных нападений на них.
Основные правила протокола. Отправитель шифрует свое сообщение открытым ключом получателя, получатель использует личный ключ для расшифрования получаемых шифрованных сообщений. Открытые ключи всех абонентов доступны всем, закрытые (личные) ключи хранятся в тайне от всех.
Шифрование: Пусть отправитель В посылает получателю А сообщение в виде исходного текста (ИТ) одного трехбуквенного слова «ДОМ»
Эти символы необходимо преобразовать в цифровую (двоичную) форму, например, ASCII кодом.
ИТ = {ИТ1 = Д = Е4 = 1110 1000, ИТ2= О=ЕЕ = 1110 1110, ИТ3 = М = ЕС = 1110 1100}
Для посимвольного шифрования сообщения абоненту В требуется открытый ключ абонента А. Этот ключ абонент А формирует и публикует как общедоступный в сети связи.
Открытый ключ А: точка генератор группы ЭК Q=P5=(3,3). Выбор этой точки достаточно произволен. Далее А вырабатывает случайное число а = 3 которое для абонента А является личным (иногда называют секретным ключом) ключом. Точка Q умножается на личный ключ. Получается точка N =аQ =3Q =3P5 = P11 =(6,3). окончательно открытый ключ имеет вид: Q,N.
Отправитель В вырабатывает свое случайное число b=2 и умножает обе точки ЭК открытого ключа Q и N на b=2: получает точки R=bQ =P4 = (2,5); S =bN = baQ = P8 = (4, 5).
Далее координаты точки S = (4, 5) преобразуются к двоичному представлению S = P8 = (4, 5) = (0000 0100, 0000 0101). Символы сообщения и координата хs преобразуются после этого в шифрованный текст (ШТ). Простейший вариант преобразования текста сообщения операцией ЕХОR
ШТ ={шт1 = 1110 1100; ШТ2 = 1110 1010; ШТ3 =1110 1000}.
Отправитель В посылает получателю А точку ЭК R и шифрованное сообщение ШТ.
Расшифрование: выполняет сторона А — получатель сообщения. Точка R кривой умножается на личный (секретный) ключ (а) абонента А: аR =аbQ = S = 3P4 = P8 = (4,5), что также дает точку S = P8 = (4,5). После этого абонент А выполняет расшифрование, получая исходный текст ИТ.
Здесь изложен весьма упрощенный вариант обмена шифрованными сообщениями, когда оба абонента используют один общий ключ. В действительности каждый символ исходного текста может представляться точкой ЭК или координатой такой точки. В последнем случае для преобразования используется групповая операция суммирования точек ЭК по модулю.
Пример 2.
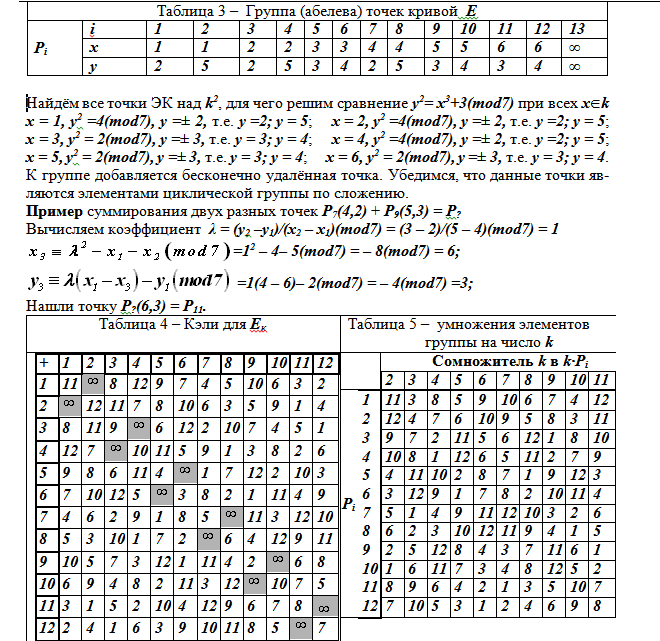
k — число слагаемых равных точке Рi соответствующей строки. В ячейках таблиц 4 и 5 помещены номера i точек Pi из таблицы 3, где представлены все 13 точек конечной аддитивной группы эллиптической кривой у2 ≡ х3 + 3(mod7)
АЛГОРИТМ ФАКТОРИЗАЦИИ ЧИСЛА
В этом вероятностном алгоритме отображены основные черты его изложения в работах [3, 7, 9].
1 Выбирается число N и числа 1< a,x,y< N;
2 полагаем b = у2 — х3 — ах(modN). После чего для ЭК у2 ≡ х3+ах +b(moN), где а, b, х, у∊Fр выбираем точку Р = (х, у);
3 Находим d = НОД(N, 4а3 + 27b2 ), если 1< d< N, то d | N и задача решена, если d = 1, то переход к следующему шагу;
4 Выбираем число k = НОК(2, 3,..., М), М — натуральное число;
5 Вычисляем кратные точки kР на ЭК, k = 2,3,..;
6 Вычисляем d = НОД(N, хk — хk-1),
если 1< d< N, то d | N задача решена, делитель N найден,
если d = 1, то либо переходим к шагу 4 и увеличиваем k, либо возвращаемся к шагу 1 и выбираем параметры новой кривой,
если d = 1, то переход к шагу 4 и уменьшаем k.
Для факторизации задается составное нечетное число n. Выбирается целое число k равное произведению степеней небольших простых чисел с ограниченными показателями степени:
k = 2d23d35d5...rdr. Здесь 2, 3, 5, ..., r несколько первых простых чисел, а d2, d3, d5,...dr -малые положительные числа. После этого вычисляется аk — 1 по модулю n и затем (n, аk — 1), что требует для вычисления 2ℓog2 (2kn) операций. При этом даже если k и n имеют в записи по тысяче знаков время расчетов оказывается вполне приемлемым.
Если (n, аk — 1) ≠ n, то получаем нетривиальный делитель числа n. При этом n раскладывается на два множителя и, если они составные, то к каждому из них применяется эта же процедура. При (n, аk -1) = n, переходим к новому выбору параметра а. Если же (n, аk — 1) = 1, то переход к новому значению k большему предыдущего. В работе [3] приводится средняя оценка сложности:
е ((2 +о(1))ℓogpℓogℓogp)1/2ℓog2N для этого алгоритма, здесь р — минимальный простой делитель N.
Конкретный числовой пример факторизации числа приводится ниже с пояснениями отдельных вычислительных элементов.
Пример 3. Этот пример показывает возможность решения решения задачи факторизации числа (составного модуля числового кольца вычетов) с использованием ЭК. В основу алгоритма положено многократное суммирование точки ЭК с собой, т.е. вычисление аддитивного порядка точки ЭК. Этот порядок делит порядок группы точек ЭК. При этом возможно, что решение задачи факторизации появляется раньше, чем будет найден порядок точки в процессе вычисления кратных точек. Нахождение суммы двух точек требует вычисления коэффициента λ, для чего привлекается расширенный алгоритм НОД(N, х2 — х1) Евклида.
Если значение d = НОД >1, и d ≠ N, то делитель N найден и факторизация выполнена. В примере все вычисления проводятся в конечном числовом кольце вычетов с модулем N = 455839= 599•761. Выбрана ЭК Е: у2 ≡ х3+ 5х -5(modN), где а = b = 5∊ ZN и дискриминант Е(а, b) равный -4а3 + 27b2 ≢ 0(modN) не сравним с нулем по модулю N. Задана также рациональная точка Р=(1,1) на ЭК. Будем многократно суммировать эту точку с собой. Рано или поздно такое суммирование приведет к результату — нейтральному элементу — точке (0), так как каждый элемент алгебраической структуры имеет период. Конечно, это суммирование очень длительный процесс, но алгоритм, оказывается, может приводить к решению часто и на промежуточном шаге вычислений. Поэтому при больших числах сначала будем находить небольшую сумму точек, например, 10! Р = 28 •34 •52•7Р = 3628800•Р и при их недостатке увеличивать число.
Начнем с удвоенной точки Р2 = 2! Р = 1•2•Р. Находим для Р2 значение λ≡(3х12 + а)(2у1)-1(modN) = (3•12 + 5)/(2•1)≡4(modN) и затем координаты точки Р2
х2 ≡ λ2 — 2х1(modN) = 42 — 2•1(modN) = 14;
у2 ≡ λ(х1 — х2) — у1(modN) = 4(1 — 14) — 1(modN) = -53(modN) => -53(modN) = 455839-53 = 455786.
При фиксированном х2, х2 ≠ 0, на ЭК имеется две точки с разными координатами у2, дополняющими друг друга до модуля. Легко убедиться подстановкой координат в уравнение ЭК, что полученная точка Р2 = ( х2, у2) лежит на ЭК.
у22 = (-53)2 = 2809 = 143 + 5•14 — 5 = 2744+70 — 5 = 2809(modN), Р2 ∊ Е.
Далее вычисляем точку Р3 = 3! Р = 1•2•3•Р=6Р =2Р+ 4Р. Находим вначале значение 2Р2 = 4Р, которое получаем суммированием точки 2Р с собой. Для 2Р2 определяем значение
λ ≡ (3х22 + а)(2у2)-1(modN) = (3•196 + 5)/(2(-53)) = — 593/106 = 322522(modN)
и затем координаты точки 2Р2
х2 ≡ λ2 — 2х1(modN) = 259851;
у2 ≡ λ(х1 — х2) — у1(modN) = 116255(modN).
При вычислениях коэффициента λ = 322522 используется арифметика поля, кольца и ЭК. Дело в том, что в алгебраических структурах отсутствует операция деления на число. Когда она появляется в формулах, ее необходимо исключить, что делается путем умножения на элемент обратный, стоящему в знаменателе формулы. Определение такого обратного элемента возможно, если элемент обратим (в конечном кольце вычетов не все элементы имеют обратные). Для выражения λ=- 593/106(mod455839) имеем как раз такой случай, т.е. для элемента 106 необходимо определить обратный к нему элемент в конечном кольце по модулю N. Покажем как это можно сделать в нашем примере; привлекается расширенный алгоритм поиска наибольшего общего делителя двух чисел: модуля 455839 и знаменателя λ числа 106:
455839 = 4300•106 + 39;
106 = 2•39 + 28;
39 = 1•28 + 11;
28 = 2•11 + 6;
11 = 1•6 + 5;
6 = 1•5 + 1. Получили, что НОД(455839, 106) = 1. После этого обратным ходом находим обратный элемент для числа 106;
1= 6 — 5 = 2•6 — 11 = 2•28 — 5•11 = 7•28 — 5•39 = 81707•106 — 19•455839 => 81707•106 — 19•455839 ≡ 1(mod455839) =>81707•106 ≡ 1(mod455839) и, окончательно, 1/106 ≡ 81707(mod455839).
Тогда λ = — 593/106(mod455839) => λ = — 593•81707(mod455839) = 322522.
Для получения точки Р3 надо суммировать две разные ранее найденные точки 2Р и 4Р. Вычисляется коэффициент λ для этого случая и координаты
х3 ≡ λ2 -х1 — х2(modN) = 195045;
у3 ≡ λ(х1 — х3) — у2(modN) = 123227(modN).
Продолжая вычисления тем же порядком для точек Р4 = 4! Р, Р5 = 5! Р… Р8 = 8! Р, для которой знаменатель в формуле для λ получает значение равное 599, в процессе вычисления d= НОД(455839, 599) получаем d = 599, т.е. это делитель N, что и завершает задачу факторизации. Другой делитель получаем делением на первый N/599 = 761. Оба делителя простые числа.
Список использованных источников
[1] Айерлэнд К., Роузен М. Классическое введение в современную теорию чисел.-М.: Мир, 1987. -416с.
[2] Болотов А.А. и др. Элементарное введение в эллиптическую криптографию.Алгебр. и алгоритмические основы.-М.: КомКнига,2006.-328 с.
[3] Василенко О.Н. Теоретико-числовые алгоритмы в криптографии.- М.: МЦНМО, 2003.-328 с.
[4] Жданов О.Н., Чалкин В.А. Эллиптические кривые. Основы теории и криптографические приложения.-М.: Кн. дом«ЛИБРОКОМ», 2012.-200с.
[5] Ишмухаметов Ш.Т. Методы факторизации натуральных чисел.- Казань: Казан.ун-т,2001.-190 с.(http://www.ksu.ru/f9/bibl/Monograph_ishm,pdf)
[6] Кнэпп Э. Эллиптические кривые.- М.: Факториал-пресс, 2004.-488 с.
[7] Koblitz N.A. Course in namber theory and cryptography.-Springer -Verlag, 1987.
[8] Lenstra H.W. (1987) Factoring integer with elliptic curves. Ann.of Math.126(2),649-673.(http://www.ams.org/mathscinet-getitem?mr=89g:11125).
[9] Соловьев Ю.П. и др. Эллиптические кривые и современные алгоритмы теории чисел.-Москва-Ижевск: Ин-т компьют-х исслед.,2003.-192с.
[10] Степанов С.А. Арифметика алгебраических кривых.- М.: Наука, 1991. — 368 с.
В работе излагается один из известных подходов к решению задачи факторизации больших чисел (ЗФБЧ), использующий математику эллиптических кривых (ЭК). Об этой математике, а точнее о технике вычислений приведу цитату авторов из [ 1 ] «Техника, используемая в настоящее время при изучении ЭК, является одной из самых изощренных во всей математике. Мы надеемся, что элементарный подход настоящей работы побудит читателя к дальнейшему изучению этой живой и пленительной ветви теории чисел. Есть много того, что следует изучить, и много работы, которую еще надо проделать. „
Удобно теоретическое изложение материала построить в сопровождении конечного числового примера и детальных отступлений и комментариев, что позволит, не перескакивая по разным частям работы, и успешней вникать в существо излагаемого материала. Понятно, что задача не из простых и требует от читателя определенной предварительной подготовки, но такова специфика “Хабра» — наличие читателей разного уровня подготовки.
Вначале приведем несколько необходимых определений высшей алгебры.
Алгебраической (конечной) группой называется множество элементов (чисел, многочленов, матриц и др.) над которыми задана одна операция. В зависимости от природы элементов (матрицы, подстановки, вычеты по модулю N) операции могут различаться, но названия их, как правило, всегда одинаковы: сложение и умножение. В случае групп вычетов по модулю N множество элементов группы может быть целыми или даже натуральными пополненными нулем числами от 0 до N — 1. Единственная операция группы по назначению может быть сложением (+), и тогда группа называется аддитивной, или умножением (•), и группа называется мультипликативной. Обеим операциям групп присущи близкие свойства (описываемые развернуто в учебной литературе): ассоциативность, замкнутость, наличие нейтрального и противоположного (обратного) элементов, а при сохранении результата операции в случае смены операндов местами — коммутативность. Поясним свойство замкнутости. Множество элементов, образующих конечную группу, конечно и постоянно. Результатами операции всегда являются элементы из исходного множества. Среди элементов группы только один — нейтральный элемент, и каждый элемент имеет себе обратный (а-1) (или противоположный (-а)). Операция над элементами не выводит результат за пределы исходного множества элементов группы. Дело в том, что в группах вычетов по модулю N операции сложение или умножение не обычные, а модулярные, т. е. для группы задается число N, называемое модулем группы, и на него делятся все получаемые результаты. Такое деление, как правило, выполняется с остатком и именно остаток принимается за окончательный результат операции.
Математик Кэли предложил характеризовать множество результатов таких операций таблицами, которые получили его имя (таблицы Кэли), таблицей сложения для аддитивной группы и таблицей умножения — для мультипликативной.
Порядок группы — число ее элементов. Каждый отдельный элемент в группе также характеризуется его порядком.
Порядок (период) элемента в группе — это наименьшее положительное число (кратность k элемента) в операции, при котором результат операции обращается в нейтральный элемент.
а+а +...+а = ka = 0 или a∙a∙a∙...∙a = ak = 1.
Период элемента кратен порядку группы, т.е. делит нацело порядок группы.
Алгебраическим числовым конечным простым полем вычетов по простому модулю N называется множество (k, GF(p), Fp) элементов (чисел от 0 до N — 1), над которыми заданы две операции сложение (+) и умножение (•). Модуль N, по которому формируются элементы поля, должен быть обязательно простым числом. Среди элементов обязательно имеются противоположные (-а) к каждому элементу и один нейтральный (0) по сложению, обратные (а-1) к каждому элементу и один нейтральный (1) по умножению. Поле образовано в соответствии с операциями допустимыми в нем (+) и (•) двумя соответствующими группами.
Кроме конечных числовых простых полей в различных теориях (кодирования, криптографии, алгебре, геометрии и т.п.) используются поля многочленов.
Такие поля GF(pn) появляются как результат расширения определенной степени n простых полей GF(p).
Расширение поля — поле GF(pn), содержащее данное поле GF(p) в качестве подполя, что записывают так К/k, где k = GF(p), К=GF(pn) — расширение поля k. Элементами поля расширения K являются все элементы (числа) простого поля k и все многочлены степени не превышающей n — 1. Иллюстрацией групп поля и результатов обеих операций в группах для примера поля GF(7) сложения и умножения являются числовые таблицы 1 и 2 помещенные ниже
Алгебраическим числовым конечным кольцом вычетов по модулю N (обозначается ZN) называется множество элементов (чисел от 0 до N — 1), над которыми заданы две операции сложение (+) и умножение (•). Модуль N, по которому формируются элементы кольца должен быть составным (не простым) числом. Если модуль сделать простым числом ( неприводимым многочленом ), то кольцо преобразуется в простое поле ( поле многочленов ). Среди элементов кольца обязательно имеются противоположные (-а) к каждому элементу и нейтральный (0) по сложению, но обратный элемент (а-1) существует не для каждого элемента и нейтральный элемент (1) по умножению в кольце может отсутствовать. Если модулем приведения является приводимый многочлен степени n, то возникает кольцо многочленов, элементами которого являются фактически те же самые элементы, что и в поле многочленов, но операции над многочленами выполняются уже не так как в поле расширения. Аналогичная ситуация с элементами возникает и для векторных пространств — они там такие же как в поле и в кольце. Операции же существенно различны. Результаты операции умножения элементов поля и тех же элементов кольца или векторного пространства будут различаться. Для нашего изложения существенно то, что не все элементы имеют обратные в мультипликативной группе кольца.
Пример 1. Пусть задано простое поле вычетов по модулю два — двоичное поле GF(2) = {0,1}. Построим поле расширения степени, например, n = 6, что обозначается так GF(26 ). Это поле образуют числа 0, 1 и все возможные многочлены степени не превышающей 5. Когда выполняются действия с многочленами в мультипликативной группе поля, то степень результата (произведения многочленов) degd(x) может превышать показатель степени n = 5. При этом условие замкнутости множества элементов мультипликативной группы нарушается. Чтобы вернуть результат в поле — сделать его элементом поля, результат произведения делят на специально выбираемый многочлен ( например, f(х) = х6 + х + 1) степени равной степени расширения, т.е. n = 6. Такой многочлен в сущности формирует поле и не должен иметь корней в простом поле, он называется неприводимым многочленом, т. е. он не раскладывается на сомножители в поле.
Говорят результаты операций поля приводятся по модулю неприводимого многочлена. Кроме того, все коэффициенты многочленов в поле принадлежат простому полю и приводятся по модулю простого поля (простого числа). Таким образом, результаты операций в поле приводятся по двойному модулю, что иногда обозначается так d(х)(moddp,f(x)), где р — простое число, формирующее простое поле, а f(x) — неприводимый многочлен степени равной степени расширения простого поля.
ЭЛЕМЕНТЫ ТЕОРИИ ЭЛЛИПТИЧЕСКОЙ КРИВОЙ
Моделирование многих явлений действительности, в частности, математических удобно выполнять с привлечением алгебраических структур: групп, полей, колец, алгебр и др. Те свойства, которые уже хорошо изучены для определенных структур, наследуются объектами, которые моделируются с использованием таких структур. Тем самым экономятся время и силы, а также и другие ресурсы. Одним из примеров использования известных свойств конечных аддитивных групп является разработка алгоритмов решения ЗФБЧ, алгоритмов цифровой подписи и/или шифрования документов (сообщений), в которых привлекаются не совсем обычные группы. В алгоритмах используются точки алгебраической кривой, заданной над конечными структурами (поле, кольцо), редуцированной (вычисления приводятся по модулю характеристики N) называемой эллиптическая кривая (ЭК) в форме Вейерштрасса, целочисленные (рациональные) точки которой образуют аддитивную группу, т. е. их можно суммировать в любом порядке, получая при этом новые точки из этой группы. При определенных условиях, накладываемых на кривую, множество таких точек замкнуто и конечно, хотя порядок группы может быть очень большим. Сама кривая плоская ее коэффициенты а и b; точки ЭК (х, у) описываются через две х и у переменные, значения которых принадлежат конечному простому полю Галуа GF(p) (но могут принадлежать и расширенному полю GF(pn), как в некоторых стандартах электронной цифровой подписи (ЭЦП)), таким образом, в алгоритмах используется декартово произведение поля GF(p)хGF(p).
Операция сложения точек ЭК — это специальная операция (+), заключительный шаг которой взятие результата по модулю N простому или (для кольца) составному. При составном модуле ЭК задана не над полем, а над кольцом, что существенно изменяет свойства рассматриваемых объектов, сохраняя основные из них.
Рассмотрим самые начальные сведения из теории и арифметики эллиптических кривых. Необходимо уяснить ряд моментов. Задание ЭК, смысловое значение параметров ЭК, множество целых точек и возможность их сложения между собой. Операция сложения точек. Эти сведения и их понимание необходимы для доступного изложения алгоритма факторизации натуральных (целых) чисел, который давно известен специалистам-криптологам по публикациям Х. Ленстра от 1987 г и более поздним усовершенствованиям Р. Монтгомери 1992 [2, 4, 5, 6, 7,10 ]. Для задания эллиптической кривой Еa,b(Fр) над полем вначале задается поле характеристикой конечного поля — простым числом N или p>3. Для задания коэффициентов а и b эллиптической кривой Е (а, b), определенной над конечным простым полем Fр, можно воспользоваться подходом из отечественного стандарта. (ГОСТ).
Таким образом, эллиптической кривой Еa,b(Fр) называется множество {(х, у)} пар чисел, элементов поля х, у∊Fр, удовлетворяющих соотношению у2 ≡ х3+ах +b(modp), где а, b∊Fр. У Еa,b(Fр) дискриминант равен -4а3 + 27b2 ≢ 0(modp) и не сравним с нулем по модулю р. Правильнее сказать так называется группа точек ЭК, а не сама кривая. Но такая замена понятий в чем-то упрощает изложение.
Коэффициенты ЭК а, b определяются соотношениями а ≡ 3k(modp); b ≡ 3k(modp);
где k ≡ J(E)(1728 — J(E))-1(modp); J(E) ≡1728∙4а3(4а3+27b2)-1(modp) инвариант ЭК; J(E) ≠ 0∨1728.
Пары чисел (х, у), удовлетворяющие уравнению ЭК, называются ее точками, обозначаемыми Q(х, у), а х и у — координатами точки. В группу точек ЭК в качестве нейтрального элемента включается специальная точка (О) — точка удаленная в бесконечность (∞ ), ее координаты обычно не вычисляются. На множестве всех целых точек ЭК вводится операция сложения (+). Для двух произвольных точек Q1(х1, у1) и Q2(х2, у2) кривой Е(а,b) суммирование выполняется по различающимся формулам в зависимости от соотношения координат точек.
При равенстве обеих координат у точек х1= х2, у1= у2≠ 0 имеем удвоение или сумму одной точки с собой. Результирующая точка Q3(х3, у3) получает координаты, вычисляемые по формулам
х3 ≡ λ2 — 2х1(modp);
у3 ≡ λ(х1 — х3) — у1(modp),
где λ ≡ (3х12 + а)(2у1)-1(modp).
При х1 ≠ х2 суммой точек Q1(х1, у1) и Q2(х2, у2) является точка Q3(х3, у3), которая получает координаты, вычисляемые по формулам
х3 ≡ λ2 — х1 — х2(modp);
у3 ≡ λ(х1-х3) — у1(modp),
где λ ≡ (у2 — у1)(х2 — х1)-1(modp).
При х1= х2, у2= — у1(modp), точки лежат на вертикальной прямой, пересекающей в них ЭК.Эта прямая пересекает и третью точку (О) ЭК, которая удалена в бесконечности. Сумма точек Q1(х1, у1) и Q2(х2, у2) называется нейтральным элементом (нулевой точкой O) группы, координаты которой не определяются. Суммирование с этой точкой любой другой точки не изменяет эту другую и дает результат Q + О = О + Q = Q.
Точка Q имеет кратность k или называется просто кратной точкой Е(а, b), если для некоторой точки Р∊Е(а, b) выполнено равенство Q = Р + Р + ...+ Р = kP. Если для точки Р выполнено Р + Р + ...+ Р = kP = О, то k — порядок точки Р.
Операция суммирования всех целых точек Е(а,b) вместе с нулевой точкой О (нейтральный элемент) порождает конечную (коммутативную) аддитивную (абелеву) группу порядка q, где q ≠ p. Для этого порядка справедливо установленное Хассе соотношение р + 1 — 2√р < q < р + 1 + 2√р.
ПРОСТАЯ КРИПТОГРАФИЧЕСКАЯ СИСТЕМА НА ЭЛЛИПТИЧЕСКИХ КРИВЫХ
В сети обмена данными для всех абонентов задается общая редуцированная эллиптическая кривая Еa,b(Fр) над полем Fр и порождающая точка Р = (х, у) на ней. Каждый абонент, используя точки аддитивной группы этой ЭК формирует свои открытый и закрытый ключи. Ниже в примере 2 рассматривается простой вариант криптографической системы (КГС) с возможностью шифрования/расшифрования сообщений элементами группы точек ЭК. Понимание основ теории эллиптических кривых и смежных вопросов открывает возможности использование богатого арсенала их средств в целях повышения уровня безопасности информационных систем и предотвращения возможных нападений на них.
Основные правила протокола. Отправитель шифрует свое сообщение открытым ключом получателя, получатель использует личный ключ для расшифрования получаемых шифрованных сообщений. Открытые ключи всех абонентов доступны всем, закрытые (личные) ключи хранятся в тайне от всех.
Шифрование: Пусть отправитель В посылает получателю А сообщение в виде исходного текста (ИТ) одного трехбуквенного слова «ДОМ»
Эти символы необходимо преобразовать в цифровую (двоичную) форму, например, ASCII кодом.
ИТ = {ИТ1 = Д = Е4 = 1110 1000, ИТ2= О=ЕЕ = 1110 1110, ИТ3 = М = ЕС = 1110 1100}
Для посимвольного шифрования сообщения абоненту В требуется открытый ключ абонента А. Этот ключ абонент А формирует и публикует как общедоступный в сети связи.
Открытый ключ А: точка генератор группы ЭК Q=P5=(3,3). Выбор этой точки достаточно произволен. Далее А вырабатывает случайное число а = 3 которое для абонента А является личным (иногда называют секретным ключом) ключом. Точка Q умножается на личный ключ. Получается точка N =аQ =3Q =3P5 = P11 =(6,3). окончательно открытый ключ имеет вид: Q,N.
Отправитель В вырабатывает свое случайное число b=2 и умножает обе точки ЭК открытого ключа Q и N на b=2: получает точки R=bQ =P4 = (2,5); S =bN = baQ = P8 = (4, 5).
Далее координаты точки S = (4, 5) преобразуются к двоичному представлению S = P8 = (4, 5) = (0000 0100, 0000 0101). Символы сообщения и координата хs преобразуются после этого в шифрованный текст (ШТ). Простейший вариант преобразования текста сообщения операцией ЕХОR
ШТ ={шт1 = 1110 1100; ШТ2 = 1110 1010; ШТ3 =1110 1000}.
Отправитель В посылает получателю А точку ЭК R и шифрованное сообщение ШТ.
Расшифрование: выполняет сторона А — получатель сообщения. Точка R кривой умножается на личный (секретный) ключ (а) абонента А: аR =аbQ = S = 3P4 = P8 = (4,5), что также дает точку S = P8 = (4,5). После этого абонент А выполняет расшифрование, получая исходный текст ИТ.
Здесь изложен весьма упрощенный вариант обмена шифрованными сообщениями, когда оба абонента используют один общий ключ. В действительности каждый символ исходного текста может представляться точкой ЭК или координатой такой точки. В последнем случае для преобразования используется групповая операция суммирования точек ЭК по модулю.
Пример 2.


k — число слагаемых равных точке Рi соответствующей строки. В ячейках таблиц 4 и 5 помещены номера i точек Pi из таблицы 3, где представлены все 13 точек конечной аддитивной группы эллиптической кривой у2 ≡ х3 + 3(mod7)
АЛГОРИТМ ФАКТОРИЗАЦИИ ЧИСЛА
В этом вероятностном алгоритме отображены основные черты его изложения в работах [3, 7, 9].
1 Выбирается число N и числа 1< a,x,y< N;
2 полагаем b = у2 — х3 — ах(modN). После чего для ЭК у2 ≡ х3+ах +b(moN), где а, b, х, у∊Fр выбираем точку Р = (х, у);
3 Находим d = НОД(N, 4а3 + 27b2 ), если 1< d< N, то d | N и задача решена, если d = 1, то переход к следующему шагу;
4 Выбираем число k = НОК(2, 3,..., М), М — натуральное число;
5 Вычисляем кратные точки kР на ЭК, k = 2,3,..;
6 Вычисляем d = НОД(N, хk — хk-1),
если 1< d< N, то d | N задача решена, делитель N найден,
если d = 1, то либо переходим к шагу 4 и увеличиваем k, либо возвращаемся к шагу 1 и выбираем параметры новой кривой,
если d = 1, то переход к шагу 4 и уменьшаем k.
Для факторизации задается составное нечетное число n. Выбирается целое число k равное произведению степеней небольших простых чисел с ограниченными показателями степени:
k = 2d23d35d5...rdr. Здесь 2, 3, 5, ..., r несколько первых простых чисел, а d2, d3, d5,...dr -малые положительные числа. После этого вычисляется аk — 1 по модулю n и затем (n, аk — 1), что требует для вычисления 2ℓog2 (2kn) операций. При этом даже если k и n имеют в записи по тысяче знаков время расчетов оказывается вполне приемлемым.
Если (n, аk — 1) ≠ n, то получаем нетривиальный делитель числа n. При этом n раскладывается на два множителя и, если они составные, то к каждому из них применяется эта же процедура. При (n, аk -1) = n, переходим к новому выбору параметра а. Если же (n, аk — 1) = 1, то переход к новому значению k большему предыдущего. В работе [3] приводится средняя оценка сложности:
е ((2 +о(1))ℓogpℓogℓogp)1/2ℓog2N для этого алгоритма, здесь р — минимальный простой делитель N.
Конкретный числовой пример факторизации числа приводится ниже с пояснениями отдельных вычислительных элементов.
Пример 3. Этот пример показывает возможность решения решения задачи факторизации числа (составного модуля числового кольца вычетов) с использованием ЭК. В основу алгоритма положено многократное суммирование точки ЭК с собой, т.е. вычисление аддитивного порядка точки ЭК. Этот порядок делит порядок группы точек ЭК. При этом возможно, что решение задачи факторизации появляется раньше, чем будет найден порядок точки в процессе вычисления кратных точек. Нахождение суммы двух точек требует вычисления коэффициента λ, для чего привлекается расширенный алгоритм НОД(N, х2 — х1) Евклида.
Если значение d = НОД >1, и d ≠ N, то делитель N найден и факторизация выполнена. В примере все вычисления проводятся в конечном числовом кольце вычетов с модулем N = 455839= 599•761. Выбрана ЭК Е: у2 ≡ х3+ 5х -5(modN), где а = b = 5∊ ZN и дискриминант Е(а, b) равный -4а3 + 27b2 ≢ 0(modN) не сравним с нулем по модулю N. Задана также рациональная точка Р=(1,1) на ЭК. Будем многократно суммировать эту точку с собой. Рано или поздно такое суммирование приведет к результату — нейтральному элементу — точке (0), так как каждый элемент алгебраической структуры имеет период. Конечно, это суммирование очень длительный процесс, но алгоритм, оказывается, может приводить к решению часто и на промежуточном шаге вычислений. Поэтому при больших числах сначала будем находить небольшую сумму точек, например, 10! Р = 28 •34 •52•7Р = 3628800•Р и при их недостатке увеличивать число.
Начнем с удвоенной точки Р2 = 2! Р = 1•2•Р. Находим для Р2 значение λ≡(3х12 + а)(2у1)-1(modN) = (3•12 + 5)/(2•1)≡4(modN) и затем координаты точки Р2
х2 ≡ λ2 — 2х1(modN) = 42 — 2•1(modN) = 14;
у2 ≡ λ(х1 — х2) — у1(modN) = 4(1 — 14) — 1(modN) = -53(modN) => -53(modN) = 455839-53 = 455786.
При фиксированном х2, х2 ≠ 0, на ЭК имеется две точки с разными координатами у2, дополняющими друг друга до модуля. Легко убедиться подстановкой координат в уравнение ЭК, что полученная точка Р2 = ( х2, у2) лежит на ЭК.
у22 = (-53)2 = 2809 = 143 + 5•14 — 5 = 2744+70 — 5 = 2809(modN), Р2 ∊ Е.
Далее вычисляем точку Р3 = 3! Р = 1•2•3•Р=6Р =2Р+ 4Р. Находим вначале значение 2Р2 = 4Р, которое получаем суммированием точки 2Р с собой. Для 2Р2 определяем значение
λ ≡ (3х22 + а)(2у2)-1(modN) = (3•196 + 5)/(2(-53)) = — 593/106 = 322522(modN)
и затем координаты точки 2Р2
х2 ≡ λ2 — 2х1(modN) = 259851;
у2 ≡ λ(х1 — х2) — у1(modN) = 116255(modN).
При вычислениях коэффициента λ = 322522 используется арифметика поля, кольца и ЭК. Дело в том, что в алгебраических структурах отсутствует операция деления на число. Когда она появляется в формулах, ее необходимо исключить, что делается путем умножения на элемент обратный, стоящему в знаменателе формулы. Определение такого обратного элемента возможно, если элемент обратим (в конечном кольце вычетов не все элементы имеют обратные). Для выражения λ=- 593/106(mod455839) имеем как раз такой случай, т.е. для элемента 106 необходимо определить обратный к нему элемент в конечном кольце по модулю N. Покажем как это можно сделать в нашем примере; привлекается расширенный алгоритм поиска наибольшего общего делителя двух чисел: модуля 455839 и знаменателя λ числа 106:
455839 = 4300•106 + 39;
106 = 2•39 + 28;
39 = 1•28 + 11;
28 = 2•11 + 6;
11 = 1•6 + 5;
6 = 1•5 + 1. Получили, что НОД(455839, 106) = 1. После этого обратным ходом находим обратный элемент для числа 106;
1= 6 — 5 = 2•6 — 11 = 2•28 — 5•11 = 7•28 — 5•39 = 81707•106 — 19•455839 => 81707•106 — 19•455839 ≡ 1(mod455839) =>81707•106 ≡ 1(mod455839) и, окончательно, 1/106 ≡ 81707(mod455839).
Тогда λ = — 593/106(mod455839) => λ = — 593•81707(mod455839) = 322522.
Для получения точки Р3 надо суммировать две разные ранее найденные точки 2Р и 4Р. Вычисляется коэффициент λ для этого случая и координаты
х3 ≡ λ2 -х1 — х2(modN) = 195045;
у3 ≡ λ(х1 — х3) — у2(modN) = 123227(modN).
Продолжая вычисления тем же порядком для точек Р4 = 4! Р, Р5 = 5! Р… Р8 = 8! Р, для которой знаменатель в формуле для λ получает значение равное 599, в процессе вычисления d= НОД(455839, 599) получаем d = 599, т.е. это делитель N, что и завершает задачу факторизации. Другой делитель получаем делением на первый N/599 = 761. Оба делителя простые числа.
Список использованных источников
[1] Айерлэнд К., Роузен М. Классическое введение в современную теорию чисел.-М.: Мир, 1987. -416с.
[2] Болотов А.А. и др. Элементарное введение в эллиптическую криптографию.Алгебр. и алгоритмические основы.-М.: КомКнига,2006.-328 с.
[3] Василенко О.Н. Теоретико-числовые алгоритмы в криптографии.- М.: МЦНМО, 2003.-328 с.
[4] Жданов О.Н., Чалкин В.А. Эллиптические кривые. Основы теории и криптографические приложения.-М.: Кн. дом«ЛИБРОКОМ», 2012.-200с.
[5] Ишмухаметов Ш.Т. Методы факторизации натуральных чисел.- Казань: Казан.ун-т,2001.-190 с.(http://www.ksu.ru/f9/bibl/Monograph_ishm,pdf)
[6] Кнэпп Э. Эллиптические кривые.- М.: Факториал-пресс, 2004.-488 с.
[7] Koblitz N.A. Course in namber theory and cryptography.-Springer -Verlag, 1987.
[8] Lenstra H.W. (1987) Factoring integer with elliptic curves. Ann.of Math.126(2),649-673.(http://www.ams.org/mathscinet-getitem?mr=89g:11125).
[9] Соловьев Ю.П. и др. Эллиптические кривые и современные алгоритмы теории чисел.-Москва-Ижевск: Ин-т компьют-х исслед.,2003.-192с.
[10] Степанов С.А. Арифметика алгебраических кривых.- М.: Наука, 1991. — 368 с.