Давным-давно, когда диоды были ещё вакуумными, J. В. Johnson впервые наблюдал мерцательный эффект в токе электронных ламп, который он так и назвал – мерцательным или фликкер-шумом. Прошло ровно 90 лет с тех пор, а фликкер-шум продолжают обнаруживать в самых разнообразных системах – от полупроводниковых приборов до разлива рек, от физики до социологии, но объяснить природу его происхождения так никто и не смог.
Даже советский фильм есть про фликкер-шум.
Вот как выглядит фликкер-шум:
Физики, пытаясь объяснить природу данного явления, естественно, ищут её в физике протекающих процессов, хотя и называют фликкер-шум аномалией. Вспомним, чему нас учат в аспирантуре на курсах по «Истории и философии науки»: аномалия (чем и является фликкер-шум) — это результат принципиальной неспособности научной парадигмы объяснить существующие факты, то есть проблему необходимо искать в теории.
Теорией в данном случае являются спектральные методы. Попробуем разобраться с этими методами, может с ними что-то не так?
По определению, фликкер-шум является сигналом, спектральная плотность мощности (или просто спектр мощности) которого описывается формулой:
где K – размерная константа, γ – безразмерная константа, которая в большинстве случаев близка к единице (в статье будем рассматривать только фликкер-шум с γ = 1).
Посмотрим на спектр мощности фликкер-шума и попробуем в нём что-нибудь увидеть.
Видно, что мощность в полосе частот от 1 Гц до бесконечности равна мощности от 0 до 1 Гц. Что такого особенного в этих двух полосах частот, что мощность в них одинаковая? Эти две полосы связывает то, что их границы являются обратными величинами друг друга, то есть 0 равен 1/бесконечность, а 1 равна 1/1. А что такое обратная величина от частоты? Это период.
Интересно, а почему в спектральном анализе используется только спектральная плотность мощности по частоте, может стоит попробовать найти спектральную плотность мощности по периоду? На этом месте все говорят – «зачем нужно от периода находить, от этого ничего не изменится». Посмотрите на рисунок.
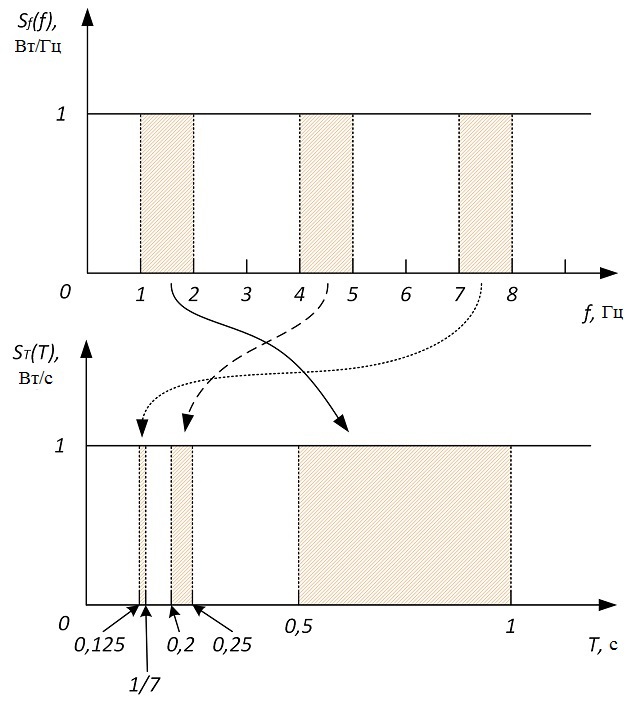
Из рисунка видно, что одной и той же полосе частот соответствуют разные полосы периодов. Значит, спектр мощности по периоду должен быть совсем другой формы. Найдём связь между спектральными плотностями мощности по частоте и по периоду. Элементарное приращение мощности равно:
где Sf(f) – спектральная плотность мощности по частоте (f-СПМ), ST(f) – спектральная плотность мощности по периоду (T-СПМ), T – период.
Знак минуса в правой части формулы (2) означает, что положительному приращению по частоте соответствует отрицательное приращение по периоду.
Из формулы (2) получим:
Как же теперь будет выглядеть фликкер-шум? Опять то же самое:
Фликкер-шум является единственным сигналом, спектр мощности которого выглядит одинаково как по частоте, так и по периоду. Если взять, к примеру, белый шум, то его T-СПМ не будет уже равномерной по периоду:
Какой же тогда сигнал будет равномерным по периоду? Да вот какой:
Это броуновский шум, его T-СПМ и f-СПМ, соответственно, определяются формулами:
Если представлять броуновский шум в виде суммы гармоник, то удобнее использовать тогда не ряд Фурье, а ряд с равномерным шагом по периоду:
где An — амплитуда n-ой гармоники, T1 – период основной гармоники, φn — фаза n-ой гармоники.
Можно ещё анимацию с суммированием гармоник сделать:
Со спектральной плотностью мощности по периоду можно ещё долго экспериментировать, но будем двигаться дальше.
Одинаково равномерным по частоте и по периоду, исходя из формулы (4), может быть только сигнал, всюду равный нулю. Какой же шум тогда считать сигналом с равномерным спектром? Попробуем вообразить сигнал с равномерным спектром и при этом не привязываться к какому-либо шагу по частоте или по периоду.
Представим, что какой-то завод выпускает генераторы синусоидального напряжения фиксированной частоты и фиксированной мощности. Все выпускаемые генераторы обладают абсолютной повторяемостью по мощности генерируемого сигнала и эта мощность равна P0. Однако повторяемость по частоте отсутствует напрочь – частота у каждого генератора может быть равна любому значению от нуля до бесконечности (хоть пГц, хоть ТГц). Теперь возьмём очень большое количество таких генераторов и подадим сигналы с их выходов на сумматор.
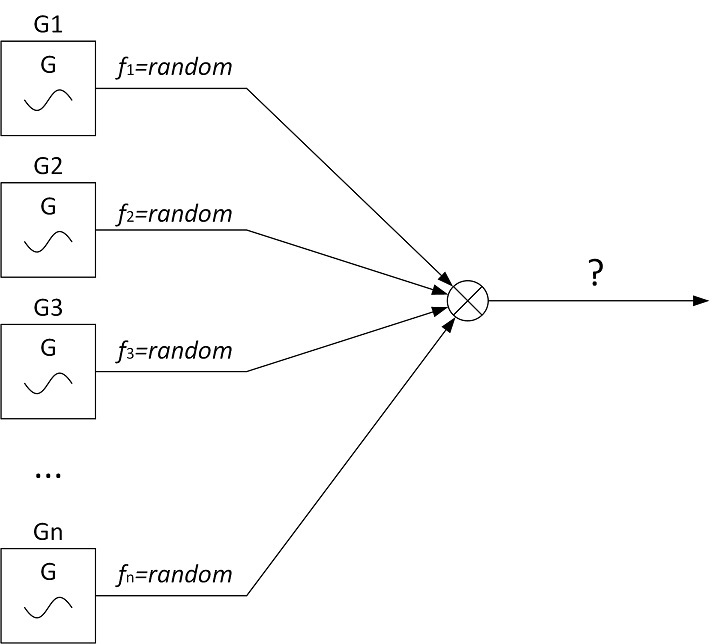
Научным языком
Здесь рассматривается такой процесс с бесконечной энергией, что каждая его реализация содержит только одну гармонику, при этом, мощность каждой реализации равна P0, а частота может принимать любое значение.
Очевидно, что сигнал на выходе сумматора должен обладать равномерным спектром. Какой же будет у него спектр мощности?
Каждый, кто знаком с основами спектрального анализа, сразу выдаст ответ – «это белый шум, так как он по определению является сигналом с равномерным спектром». Давайте это проверим.
Для начала, нужно каким-то образом связать мощность каждого генератора с его частотой. В этом месте может возникнуть вопрос – «что тут связывать, если она не зависит от частоты?», тогда встречный вопрос – от периода она тоже не зависит? В качестве такого связующего звена можно использовать энергию одного периода синусоиды:
Мощность генератора равна:
Теперь найдём функцию, которая будет показывать зависимость мощности генераторов от их частоты:
где ET(f) – зависимость энергии периода синусоиды генератора от частоты.
Мощность, приходящаяся на полосу частот df, будет равна:
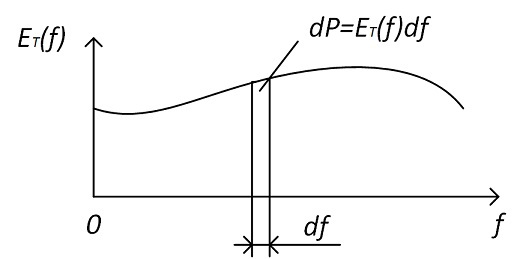
Если посмотрим на формулы (2) и (14), то мы увидим, что:
Замечательно, теперь из формулы (12) найдём спектр мощности:
Сигнал на выходе сумматора — фликкер-шум. Цвет этого шума – розовый (по мне, так он белый).
А теперь ответ на вопрос 90-летней давности:
Механизм возникновения фликкер-шума очень прост: если объект излучает гармонический сигнал произвольной частоты с мощностью P0, то множество таких объектов будет излучать сигнал со спектром фликкер-шума.
Истинный сигнал с равномерным спектром является фликкер-шумом. Любопытно, что же это за спектральная координата, относительно которой фликкер-шум выглядит равномерным.
Допустим, что генерируемые синусоиды различаются как по частоте, так и по мощности, тогда формула (16) запишется в следующем виде:
где P(f) – мощность реализации с частотой f.
Так как для процесса с равномерным спектром P(f) = P0, то P(f) удобно рассматривать как спектральную плотность мощности по некоторой величине Φ (Φ-СПМ):
По определению, спектральная плотность мощности должна иметь размерность мощности, делённой на размерность спектральной координаты. В данном случае Φ-СПМ имеет размерность мощности, следовательно, её спектральная координата Φ должна быть безразмерной. Таким образом, Φ-СПМ будет являться одновременно и спектральной плотностью мощности и зависимостью мощности генератора от частоты. Мощность в полосе частот df должна быть равна мощности в полосе dΦ:
Из формул (17), (18) и (19), получим:
и Φ определится по формуле:
Для исключения логарифмирования размерной величины, примем:
где f0 – некоторая частота, равная 1 Гц,
тогда:
Совершенно бессмысленную константу f0 мне пришлось ввести из-за того, что логарифмирование размерной величины у физиков вызывает fatal error.
А теперь мы можем представить фликкер-шум в виде суммы гармоник с одинаковыми амплитудами:
где An — амплитуда n-ой гармоники, Ф1 – Ф основной гармоники, φn — фаза n-ой гармоники.
Сделаем анимацию:
Можно ещё анимацию для одинаковых начальных фаз сделать:
Если объединим формулы (4), (17), (18), то получим красивое выражение:
Скажу ещё пару слов по квантовой механике.
Кроме спектральной плотности мощности существует ещё спектральная плотность энергии (СПЭ). Отличие их в том, что СПЭ используется для процессов с конечной энергией, а СПМ для процессов с бесконечной энергией. СПЭ характеризует энергию, приходящуюся на единицу полосы частот. А что нам мешает сделать тоже самое для процессов с конечной энергией? СПЭ по разным спектральным координатам будут связаны аналогичной формулой:
где Wf(f) – спектральная плотность энергии по частоте (f-СПЭ), WФ(Ф) – спектральная плотность энергии по Φ (Φ-СПЭ), WT(T) – спектральная плотность энергии по периоду (T-СПЭ).
Левая часть формулы (26) Вам ничего не напоминает? Эту формулу можно легко преобразовать в формулу для энергии кванта.
Давайте представим, что рассматриваемые выше генераторы выдают сигналы с произвольными частотами и произвольными мощностями, но энергия этих сигналов конечна. В природе подобные генераторы, мягко говоря, очень распространены – это электроны, а генерируемые ими сигналы – это кванты энергии.
Φ-СПЭ на конкретной частоте равна энергии:
Если принять f-СПЭ равной постоянной Планка, то формула (29) преобразуется в формулу для энергии кванта (28).
Так как постоянная Планка не зависит от частоты, то её можно рассматривать как равномерную f-СПЭ процесса, каждая реализация которого соответствует излучению электроном одного кванта энергии с произвольной частотой.
Если поделить f-СПЭ электромагнитной волны на постоянную Планка, то можно получить зависимость числа квантов волны от частоты. И так далее…
Вывод: фликкер-шум — сигнал с равномерным спектром, спектр которого искажается преобразованием Фурье.
Буду рад любой критике по статье.
Приложение А
Если процесс представлен функциями P(f) и ET(f):

то спектр мощности такого процесса можно найти как производную P(f) по частоте:

Элементарное приращение тогда определится по формуле:

В этом случае появляется функция, равная производной зависимости энергии за период по частоте (с размерностью Дж/Гц).
Рассмотрим процесс, обладающий следующей ET(f):

Если γ = 1, то рассматриваемый процесс обладает равномерным непрерывным спектром (в соответствии с формулой (А.1)).
Определим по формуле (А.3) спектр мощности процесса, соответствующего формуле (А.5):

Обозначим:

и получим формулу (1):

Чем ближе γ к единице, тем равномернее спектр, однако K при этом уменьшается. В пределе, когда γ = 1 получается спектр мощности фликкер-шума с K = 0.
Для спектра мощности по периоду получается аналогичный результат.
Если γ = 0, то спектр мощности будет соответствовать белому шуму. Из формул (А.5) и (А.1) видно, что процесс с γ = 0 (белый шум) не обладает равномерным спектром:

то спектр мощности такого процесса можно найти как производную P(f) по частоте:
Элементарное приращение тогда определится по формуле:
В этом случае появляется функция, равная производной зависимости энергии за период по частоте (с размерностью Дж/Гц).
Рассмотрим процесс, обладающий следующей ET(f):
Если γ = 1, то рассматриваемый процесс обладает равномерным непрерывным спектром (в соответствии с формулой (А.1)).
Определим по формуле (А.3) спектр мощности процесса, соответствующего формуле (А.5):

Обозначим:
и получим формулу (1):
Чем ближе γ к единице, тем равномернее спектр, однако K при этом уменьшается. В пределе, когда γ = 1 получается спектр мощности фликкер-шума с K = 0.
Для спектра мощности по периоду получается аналогичный результат.
Если γ = 0, то спектр мощности будет соответствовать белому шуму. Из формул (А.5) и (А.1) видно, что процесс с γ = 0 (белый шум) не обладает равномерным спектром:

Приложение Б
Рассмотрим сетку частот с равномерным шагом, стремящимся к нулю. Так как частотный шаг стремится к нулю, то такая сетка частот содержит в себе все возможные частоты и определены они в точках n*df.
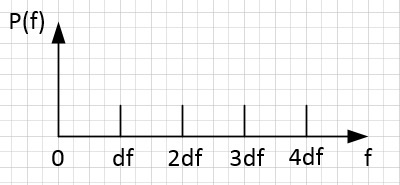
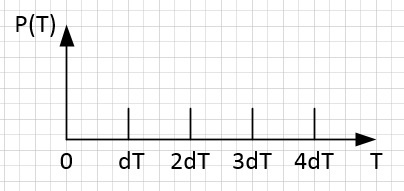
Рассмотрим также сетку периодов с равномерным шагом, стремящимся к нулю. Так как периодный шаг стремится к нулю, то такая сетка периодов содержит в себе все возможные периоды и определены они в точках n*dT.
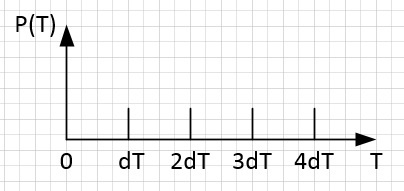
Если сопоставить сетку частот и сетку периодов, то можно увидеть, что есть периоды, которым невозможно сопоставить частоту (попадают на интервал от n*df до (n+1)*df), и наоборот.

Если частоте невозможно сопоставить период, а также если периоду невозможно сопоставить частоту, то их следует удалить из соответствующей сетки, так как они не существуют. То есть каждая сетка содержит лишние частоты и периоды. Если удалить все частоты и периоды, которым невозможно сопоставить период и частоту, то получим некоторый новый неравномерный шаг по частоте, равный неравномерному шагу по периоду. Такой шаг соответствует равномерному шагу по логарифму частоты, равный по модулю равномерному шагу по логарифму периода. Процессом, обладающим равномерным по логарифму частоты спектром, является фликкер-шум.

Рассмотрим также сетку периодов с равномерным шагом, стремящимся к нулю. Так как периодный шаг стремится к нулю, то такая сетка периодов содержит в себе все возможные периоды и определены они в точках n*dT.
Если сопоставить сетку частот и сетку периодов, то можно увидеть, что есть периоды, которым невозможно сопоставить частоту (попадают на интервал от n*df до (n+1)*df), и наоборот.

Если частоте невозможно сопоставить период, а также если периоду невозможно сопоставить частоту, то их следует удалить из соответствующей сетки, так как они не существуют. То есть каждая сетка содержит лишние частоты и периоды. Если удалить все частоты и периоды, которым невозможно сопоставить период и частоту, то получим некоторый новый неравномерный шаг по частоте, равный неравномерному шагу по периоду. Такой шаг соответствует равномерному шагу по логарифму частоты, равный по модулю равномерному шагу по логарифму периода. Процессом, обладающим равномерным по логарифму частоты спектром, является фликкер-шум.
Приложение В
Известно, что дельта-функция обладает равномерным спектром. Определим её спектральную плотность мощности по частоте и по периоду.
Коэффициенты ряда Фурье в комплексной форме определяются по формуле:
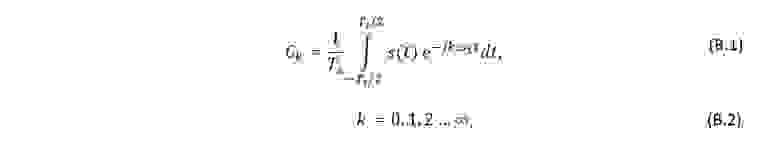
где ω1 – основная частота.
Если s(t) является дельта-функцией, то все коэффициенты Ck будут принимать одно и то же значение, независимо от k, причём значение основной частоты может быть любым.
Но ничто не мешает использовать вместо последовательности целых чисел любую другую последовательность. Если взять, например, последовательность чисел, обратную целым:
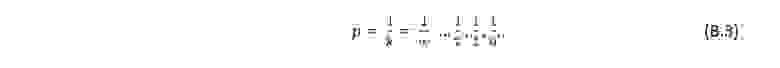
то формула (В.1) примет вид
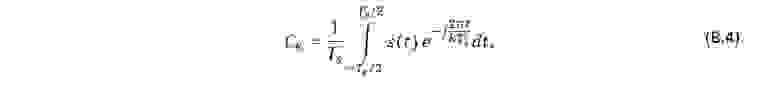
где T1 – основной период,
и будет получен дискретный спектр с равномерным шагом по периоду. В данном случае для дельта-функции значение коэффициентов Ck также принимает одно и то же значение, и значение периода основной гармоники также может быть любым.
Если перейти к непрерывным спектрам мощности по частоте и по периоду, то получим, что и тот и другой спектр мощности является независимым от своего аргумента функцией, что противоречит формуле (4). Получается, что спектр мощности дельта-функции зависит от метода его определения.
Попробуем определить, какие значения частот и периодов вообще возможны. Частота и период могут принимать любое значение от 0 до бесконечности по двум причинам:
1) Ось времени непрерывна – частоту можно увеличивать в бесконечное число раз, соответственно период можно уменьшать в бесконечное число раз.
2) Ось времени бесконечна – частоту можно уменьшать в бесконечное число раз, соответственно период можно увеличивать в бесконечное число раз.
Определим сначала спектр ограниченной во времени периодически продолженной и дискретной во временной области дельта-функции. Затем устремим к нулю шаг дискретизации и к бесконечности период повторения дельта-функции, в результате получим непрерывный спектр дельта-функции.
Известно, что периодический во временной области сигнал обладает дискретным спектром. Спектр такого сигнала представляется в виде сетки частот, полученных умножением частоты, равной f0 = 1 / (период сигнала) на целое число. В случае дельта-функции получаем набор гармоник с равномерным шагом по частоте с одинаковыми амплитудами.
Известно, что дискретный во временной области сигнал обладает периодическим спектром. Никаких ограничений на возможные значения частот нет (кроме условия, что частота в спектре должна быть меньше частоты Найквиста для восстановления).
Рассмотрим периодические дискретные сигналы:
a) Если сигнал является дискретным, то он определён только в некоторых конкретных точках: tn = n * Δt, где n – целое число, Δt – шаг дискретизации.
b) Если сигнал является периодическим, то все его значения повторяются через период времени: s(t) = s(t + T), где T – период сигнала.
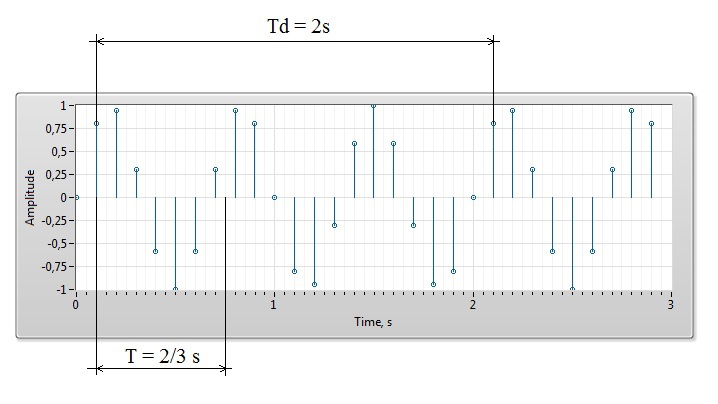
c) Если сигнал является дискретным и периодическим, то все его значения повторяются через период времени, кратный шагу дискретизации s(tn) = s(tn + Td), где Td – период сигнала, являющийся суммой целого числа Δt. Это объясняется тем, что сигнал с периодом, состоящим из дробного числа Δt, через период не повторит своего значения, так как попадёт на несуществующее время. Получается, что ограничение на возможные значения частот всё же есть.
Например, если гармонический сигнал с частотой 1,5 Гц оцифровать с частотой дискретизации 10 Гц, то получается периодический сигнал с частотой 0,5 Гц.
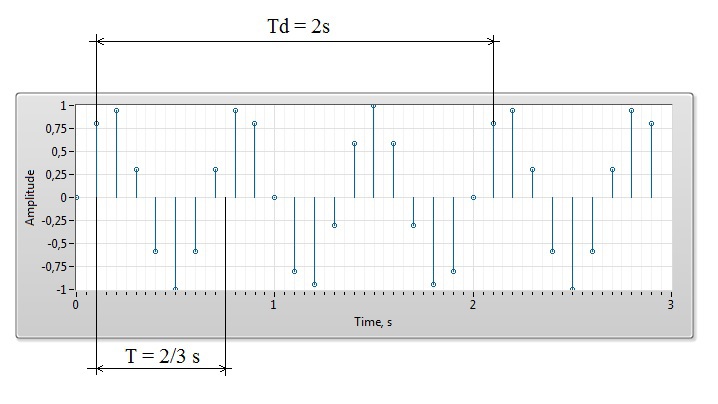
Таким образом, дискретный во времени сигнал может быть периодическим только с периодом, кратным шагу дискретизации Δt, и спектр такого сигнала может состоять только из периодов Tn = n * Δt, где n – целое число. В случае дельта-функции получаем набор гармоник с равномерным шагом по периоду с одинаковыми амплитудами.
Теперь определим спектр ограниченной во времени периодически продолженной и дискретной во времени дельта-функции. Такой спектр может состоять только из частот fn, кратных f0 и периодов Tn, кратных Δt. Если какая-то из частот fn не совпадает ни с одной из 1/Tn, то это уже не частота fn, а какая-то другая из набора 1/Tn. Таким образом, если частотe fn не удаётся сопоставить ни один из периодов из набора Tn, то её следует удалить из набора fn, так как сигнал с такой частотой нереализуем при заданном шаге дискретизации. Если удалить из сетки частот все частоты, которым невозможно сопоставить период, то получаем новый неравномерный по частоте шаг, равный неравномерному шагу по периоду. Таким неравномерным шагом является равномерный шаг по логарифму частоты. Сигналом с равномерным по логарифму частоты спектром является фликкер-шум. Если устремить к нулю шаг дискретизации и к бесконечности период повторения дельта-функций, то получаем непрерывный спектр дельта-функции, совпадающий со спектром фликкер-шума.
Коэффициенты ряда Фурье в комплексной форме определяются по формуле:
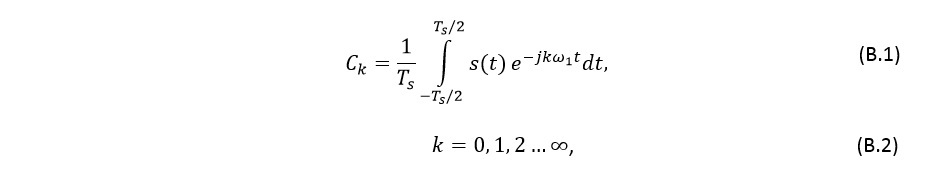
где ω1 – основная частота.
Если s(t) является дельта-функцией, то все коэффициенты Ck будут принимать одно и то же значение, независимо от k, причём значение основной частоты может быть любым.
Но ничто не мешает использовать вместо последовательности целых чисел любую другую последовательность. Если взять, например, последовательность чисел, обратную целым:
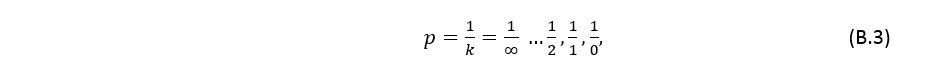
то формула (В.1) примет вид
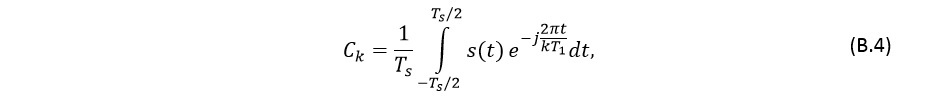
где T1 – основной период,
и будет получен дискретный спектр с равномерным шагом по периоду. В данном случае для дельта-функции значение коэффициентов Ck также принимает одно и то же значение, и значение периода основной гармоники также может быть любым.
Если перейти к непрерывным спектрам мощности по частоте и по периоду, то получим, что и тот и другой спектр мощности является независимым от своего аргумента функцией, что противоречит формуле (4). Получается, что спектр мощности дельта-функции зависит от метода его определения.
Попробуем определить, какие значения частот и периодов вообще возможны. Частота и период могут принимать любое значение от 0 до бесконечности по двум причинам:
1) Ось времени непрерывна – частоту можно увеличивать в бесконечное число раз, соответственно период можно уменьшать в бесконечное число раз.
2) Ось времени бесконечна – частоту можно уменьшать в бесконечное число раз, соответственно период можно увеличивать в бесконечное число раз.
Определим сначала спектр ограниченной во времени периодически продолженной и дискретной во временной области дельта-функции. Затем устремим к нулю шаг дискретизации и к бесконечности период повторения дельта-функции, в результате получим непрерывный спектр дельта-функции.
Известно, что периодический во временной области сигнал обладает дискретным спектром. Спектр такого сигнала представляется в виде сетки частот, полученных умножением частоты, равной f0 = 1 / (период сигнала) на целое число. В случае дельта-функции получаем набор гармоник с равномерным шагом по частоте с одинаковыми амплитудами.
Известно, что дискретный во временной области сигнал обладает периодическим спектром. Никаких ограничений на возможные значения частот нет (кроме условия, что частота в спектре должна быть меньше частоты Найквиста для восстановления).
Рассмотрим периодические дискретные сигналы:
a) Если сигнал является дискретным, то он определён только в некоторых конкретных точках: tn = n * Δt, где n – целое число, Δt – шаг дискретизации.
b) Если сигнал является периодическим, то все его значения повторяются через период времени: s(t) = s(t + T), где T – период сигнала.
c) Если сигнал является дискретным и периодическим, то все его значения повторяются через период времени, кратный шагу дискретизации s(tn) = s(tn + Td), где Td – период сигнала, являющийся суммой целого числа Δt. Это объясняется тем, что сигнал с периодом, состоящим из дробного числа Δt, через период не повторит своего значения, так как попадёт на несуществующее время. Получается, что ограничение на возможные значения частот всё же есть.
Например, если гармонический сигнал с частотой 1,5 Гц оцифровать с частотой дискретизации 10 Гц, то получается периодический сигнал с частотой 0,5 Гц.
Таким образом, дискретный во времени сигнал может быть периодическим только с периодом, кратным шагу дискретизации Δt, и спектр такого сигнала может состоять только из периодов Tn = n * Δt, где n – целое число. В случае дельта-функции получаем набор гармоник с равномерным шагом по периоду с одинаковыми амплитудами.
Теперь определим спектр ограниченной во времени периодически продолженной и дискретной во времени дельта-функции. Такой спектр может состоять только из частот fn, кратных f0 и периодов Tn, кратных Δt. Если какая-то из частот fn не совпадает ни с одной из 1/Tn, то это уже не частота fn, а какая-то другая из набора 1/Tn. Таким образом, если частотe fn не удаётся сопоставить ни один из периодов из набора Tn, то её следует удалить из набора fn, так как сигнал с такой частотой нереализуем при заданном шаге дискретизации. Если удалить из сетки частот все частоты, которым невозможно сопоставить период, то получаем новый неравномерный по частоте шаг, равный неравномерному шагу по периоду. Таким неравномерным шагом является равномерный шаг по логарифму частоты. Сигналом с равномерным по логарифму частоты спектром является фликкер-шум. Если устремить к нулю шаг дискретизации и к бесконечности период повторения дельта-функций, то получаем непрерывный спектр дельта-функции, совпадающий со спектром фликкер-шума.