Пьер Ферма утверждал, что:
Как же подойти к доказательству этого утверждения Ферма?

(картинка для привлечения внимания)
Представим себе, что мы нашли или построили прямоугольный треугольник со следующими сторонами: катеты —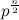 ,
, 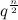 и гипотенузой
и гипотенузой 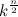 где (p, q, k, n) — числа натуральные. Тогда по теореме Пифагора получим
где (p, q, k, n) — числа натуральные. Тогда по теореме Пифагора получим 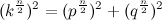 или
или 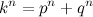 . Таким образом, если мы найдем или построим такой треугольник, то мы опровергнем Ферма. Если же мы докажем, что такой треугольник не существует, то мы докажем теорему.
. Таким образом, если мы найдем или построим такой треугольник, то мы опровергнем Ферма. Если же мы докажем, что такой треугольник не существует, то мы докажем теорему.
Так как в утверждении речь идёт о натуральных числах, то найдем, чему равняется разность квадратов двух нечетных натуральных чисел. Т.е. решим уравнение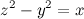 . Для этого построим прямоугольные треугольники, гипотенуза которых равна
. Для этого построим прямоугольные треугольники, гипотенуза которых равна 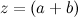 , а катет равен
, а катет равен 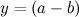 , где
, где 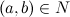 и (a > b). Тогда по теореме Пифагора можно вычислить второй катет по формуле
и (a > b). Тогда по теореме Пифагора можно вычислить второй катет по формуле 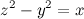 (1), или
(1), или 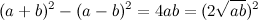 (2). Мы получили, что стороны этих треугольников равны
(2). Мы получили, что стороны этих треугольников равны 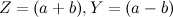 и
и 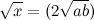 . Таким образом, мы можем перебрать все пары чисел a и b из натурального множества (назовем эти числа “генераторами” данного тождества) и получить все возможные треугольники с заданными свойствами
. Таким образом, мы можем перебрать все пары чисел a и b из натурального множества (назовем эти числа “генераторами” данного тождества) и получить все возможные треугольники с заданными свойствами 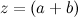 ,
, 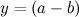 . Докажем необходимость данного решения. Перепишем
. Докажем необходимость данного решения. Перепишем 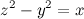 (1) в виде
(1) в виде 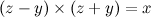 . Так как Z и Y нечетные числа, значит можно написать ( Z — Y ) = 2b и (Z + Y )=2a. Решая их относительно Z и Y, получим Z = (a + b) и Y = (a — b). Тогда можно записать, что X = 4ab и, подставляя эти значения в
. Так как Z и Y нечетные числа, значит можно написать ( Z — Y ) = 2b и (Z + Y )=2a. Решая их относительно Z и Y, получим Z = (a + b) и Y = (a — b). Тогда можно записать, что X = 4ab и, подставляя эти значения в 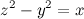 (1), получим
(1), получим 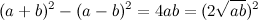 .
.
Чтобы избежать получения подобных треугольников, и, учитывая, что Z и Y — нечетные числа по условию, числа a и b должны быть взаимно простыми и разной четности. Далее будем считать, что четным является число a. Для того, чтобы упорядочить распределение прямоугольных треугольников в множестве натуральных чисел N, поступим следующим образом: из этого множества вычтем все числа, которые являются четными степенями натуральных чисел. Обозначим это множество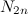 , где n — натуральное число. Затем из оставшихся натуральных чисел вычтем все числа, которые являются нечетными (≥3) степенями натуральных чисел и обозначим множество этих чисел как
, где n — натуральное число. Затем из оставшихся натуральных чисел вычтем все числа, которые являются нечетными (≥3) степенями натуральных чисел и обозначим множество этих чисел как 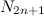 . Оставшиеся натуральные числа составят множество, числа которого есть натуральные числа в первой степени. Обозначим это множество
. Оставшиеся натуральные числа составят множество, числа которого есть натуральные числа в первой степени. Обозначим это множество 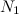 . Очевидно, соединение этих 3-х множеств есть множество натуральных чисел, или
. Очевидно, соединение этих 3-х множеств есть множество натуральных чисел, или 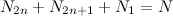 . Множество
. Множество 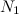 представим как ряд
представим как ряд 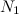 = {1, 2, 3, 5, 6, 7, 10, 11, 12, 13, 14, 15, 17,………}. Представим множества
= {1, 2, 3, 5, 6, 7, 10, 11, 12, 13, 14, 15, 17,………}. Представим множества 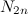 и
и 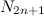 в виде рядов. Тогда множество
в виде рядов. Тогда множество 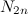 будет представлять собой матрицу, состоящую из бесконечного числа строк, каждая строка будет состоять из чисел ряда
будет представлять собой матрицу, состоящую из бесконечного числа строк, каждая строка будет состоять из чисел ряда 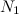 , возведенных в степень 2n, а n — есть номер строки. Так первая строка состоит из квадратов всех чисел ряда
, возведенных в степень 2n, а n — есть номер строки. Так первая строка состоит из квадратов всех чисел ряда 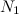 , вторая строка состоит из 4-х степеней этих чисел и т.д. Рассмотрим множество
, вторая строка состоит из 4-х степеней этих чисел и т.д. Рассмотрим множество 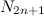 , которое будет представлять собой матрицу, состоящую из бесконечного числа строк, каждая строка которой будет состоять из чисел ряда
, которое будет представлять собой матрицу, состоящую из бесконечного числа строк, каждая строка которой будет состоять из чисел ряда 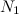 , возведенных в степень 2n+1. (n — есть номер строки). Так первая строка этой матрицы состоит из кубов чисел ряда
, возведенных в степень 2n+1. (n — есть номер строки). Так первая строка этой матрицы состоит из кубов чисел ряда 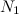 , вторая строка состоит из чисел ряда
, вторая строка состоит из чисел ряда 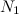 в пятой степени и т.д. Рассмотрим множество
в пятой степени и т.д. Рассмотрим множество 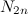 . Т.к.
. Т.к. 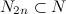 , то примем тот же алгоритм построения треугольников (см. выше). Найдем «генераторы» тождества, Это будут числа
, то примем тот же алгоритм построения треугольников (см. выше). Найдем «генераторы» тождества, Это будут числа 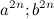 , где
, где 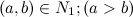 , составим тождество:
, составим тождество: 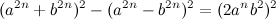 (3), мы получили множество прямоугольных треугольников с целочисленными сторонами. Здесь
(3), мы получили множество прямоугольных треугольников с целочисленными сторонами. Здесь 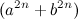 — гипотенуза,
— гипотенуза, 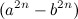 — катет и
— катет и 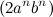 — второй катет. Для опровержения утверждения Ферма нужно, чтобы стороны X, Y, Z искомого треугольника равнялись
— второй катет. Для опровержения утверждения Ферма нужно, чтобы стороны X, Y, Z искомого треугольника равнялись 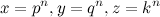 (4). Где (p, q, k, n) — натуральные числа. По теореме Пифагора будем иметь
(4). Где (p, q, k, n) — натуральные числа. По теореме Пифагора будем иметь 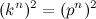 или
или 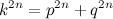 и утверждение Ферма будет опровергнуто. Из тождества
и утверждение Ферма будет опровергнуто. Из тождества 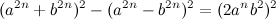 видно, что
видно, что 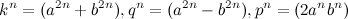 . Рассмотрим последнее равенство
. Рассмотрим последнее равенство 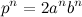 , в этом равенстве «p» ни при каких значениях «a и b»
, в этом равенстве «p» ни при каких значениях «a и b» 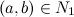 не будет натуральным числом, если
не будет натуральным числом, если 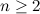 . Это означает, что в рассмотренном множестве треугольников не существует ни одного треугольника с искомыми сторонами (4).
. Это означает, что в рассмотренном множестве треугольников не существует ни одного треугольника с искомыми сторонами (4).
Теперь рассмотрим множество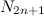 . Обозначим (2n+1) как «m», тогда во множестве
. Обозначим (2n+1) как «m», тогда во множестве 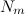 получим прямоугольные треугольники, описываемые тождеством
получим прямоугольные треугольники, описываемые тождеством 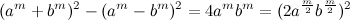 (6). Если мы сможем построить прямоугольный треугольник X, Y, Z со сторонами
(6). Если мы сможем построить прямоугольный треугольник X, Y, Z со сторонами 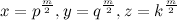 (7), где
(7), где 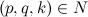 , то мы опровергнем утверждение Ферма, т.к. по теореме Пифагора
, то мы опровергнем утверждение Ферма, т.к. по теореме Пифагора 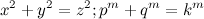 и (p, q и k) — натуральные числа. Надо, чтобы
и (p, q и k) — натуральные числа. Надо, чтобы 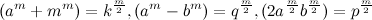 . Рассматривая последнее равенство заметим, что «p» не может быть натуральным числом ни при каких значениях «a и b»,
. Рассматривая последнее равенство заметим, что «p» не может быть натуральным числом ни при каких значениях «a и b», 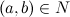 , если
, если 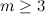 . Значит и в этом множестве треугольников не существует ни одного треугольника с искомыми сторонами (7).
. Значит и в этом множестве треугольников не существует ни одного треугольника с искомыми сторонами (7).
Однако из вышесказанного видно, что все доказательство сводится к анализу числа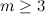
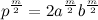 , где «
, где «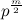 » при любых натуральных «a и b» не будет натуральным числом в степени «m/2». Или же
» при любых натуральных «a и b» не будет натуральным числом в степени «m/2». Или же 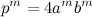 (8) при тех же условиях не будет натуральным числом в степени «m». Из доказательства видно, что «генераторами» тождества (6) являются числа «
(8) при тех же условиях не будет натуральным числом в степени «m». Из доказательства видно, что «генераторами» тождества (6) являются числа «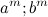 » из ряда
» из ряда 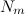 Но, анализируя
Но, анализируя 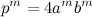 (8), можно подставить вместо «
(8), можно подставить вместо «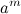 » число
» число 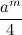 . Так как
. Так как 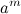 есть четное число, (см.Примечание), то
есть четное число, (см.Примечание), то 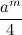 — натуральное число. После подстановки его в (8) получим
— натуральное число. После подстановки его в (8) получим 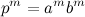 , то есть натуральные числа в степени «m». Совершив вышеуказанную подстановку в тождество (6), и, обозначив
, то есть натуральные числа в степени «m». Совершив вышеуказанную подстановку в тождество (6), и, обозначив 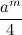 через
через 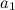 , получим следующее тождество:
, получим следующее тождество: 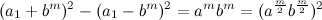 . Мы получили множество прямоугольных треугольников со сторонами
. Мы получили множество прямоугольных треугольников со сторонами 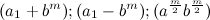 . Если ( k,q, p) — натуральные числа в нечетной степени, т.е.
. Если ( k,q, p) — натуральные числа в нечетной степени, т.е. 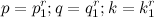 где r — любое нечетное число, а
где r — любое нечетное число, а 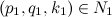 . Чтобы опровергнуть Ферма нужно, чтобы:
. Чтобы опровергнуть Ферма нужно, чтобы: 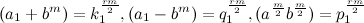 В последнем равенстве при любых натуральных a и b,
В последнем равенстве при любых натуральных a и b, 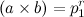 — числа натуральные, но первые два равенства невозможны, так как, если «m и r» любые нечетные числа, то
— числа натуральные, но первые два равенства невозможны, так как, если «m и r» любые нечетные числа, то 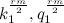 — иррациональные числа, а числа в скобках — числа натуральные. Если же (k,q, p) — натуральные числа в четной степени, т.е.
— иррациональные числа, а числа в скобках — числа натуральные. Если же (k,q, p) — натуральные числа в четной степени, т.е. 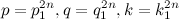 , то мы получим следующие равенства
, то мы получим следующие равенства 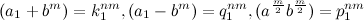 (5). В данном варианте последнее равенство невозможно, т.к. извлекая корень m степени из обеих частей равенства получим
(5). В данном варианте последнее равенство невозможно, т.к. извлекая корень m степени из обеих частей равенства получим 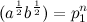 , т.е. в скобках иррациональное число, а
, т.е. в скобках иррациональное число, а 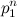 — натуральное. Это значит, что и в этом множестве не найдено «нужного» треугольника. А это значит, что для любых нечетных «m» утверждение Ферма верно, а значит, верно, для всех простых показателей «m ≥ 3».
— натуральное. Это значит, что и в этом множестве не найдено «нужного» треугольника. А это значит, что для любых нечетных «m» утверждение Ферма верно, а значит, верно, для всех простых показателей «m ≥ 3».
Остается найти доказательство теоремы для четных показателей. Из (5) следует, что, если в каноническом разложении четного показателя степени есть нечетное простое число, то утверждение Ферма для этой степени верно. Очевидно, что этому условию отвечают все четные числа, кроме числа «4» и чисел кратных четырем, т.е. 8, 16, 32, 64 … и т.д. В разложении этих чисел есть только простое число 2. Поэтому вышеприведенное доказательство не дает ответа для этих степеней.
Значит остается доказать теорему для «n = 4». Можно предположить, что у Ферма было общее доказательство, но не полное. Может быть, поэтому он и не записал свое доказательство. И только через несколько лет, создав свой метод «бесконечного или неопределенного спуска», он доказал, что не существует прямоугольного треугольника с целочисленными сторонами, у которого площадь равнялась бы квадрату натурального числа. После этого доказательство теоремы для «n = 4» не составило труда. Это доказательство Ферма записал. И теорема оказалась доказанной полностью.
невозможно разложить куб на два куба или биквадрат на два биквадрата и вообще невозможно разложить какую-либо степень, большую чем два, на две степени с таким же показателем.
Как же подойти к доказательству этого утверждения Ферма?

(картинка для привлечения внимания)
Представим себе, что мы нашли или построили прямоугольный треугольник со следующими сторонами: катеты —
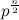 ,
, 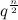 и гипотенузой
и гипотенузой 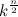 где (p, q, k, n) — числа натуральные. Тогда по теореме Пифагора получим
где (p, q, k, n) — числа натуральные. Тогда по теореме Пифагора получим 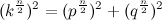 или
или 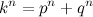 . Таким образом, если мы найдем или построим такой треугольник, то мы опровергнем Ферма. Если же мы докажем, что такой треугольник не существует, то мы докажем теорему.
. Таким образом, если мы найдем или построим такой треугольник, то мы опровергнем Ферма. Если же мы докажем, что такой треугольник не существует, то мы докажем теорему.Так как в утверждении речь идёт о натуральных числах, то найдем, чему равняется разность квадратов двух нечетных натуральных чисел. Т.е. решим уравнение
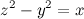 . Для этого построим прямоугольные треугольники, гипотенуза которых равна
. Для этого построим прямоугольные треугольники, гипотенуза которых равна 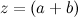 , а катет равен
, а катет равен 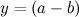 , где
, где 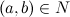 и (a > b). Тогда по теореме Пифагора можно вычислить второй катет по формуле
и (a > b). Тогда по теореме Пифагора можно вычислить второй катет по формуле 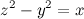 (1), или
(1), или 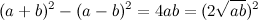 (2). Мы получили, что стороны этих треугольников равны
(2). Мы получили, что стороны этих треугольников равны 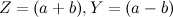 и
и 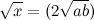 . Таким образом, мы можем перебрать все пары чисел a и b из натурального множества (назовем эти числа “генераторами” данного тождества) и получить все возможные треугольники с заданными свойствами
. Таким образом, мы можем перебрать все пары чисел a и b из натурального множества (назовем эти числа “генераторами” данного тождества) и получить все возможные треугольники с заданными свойствами 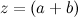 ,
, 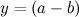 . Докажем необходимость данного решения. Перепишем
. Докажем необходимость данного решения. Перепишем 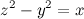 (1) в виде
(1) в виде 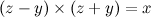 . Так как Z и Y нечетные числа, значит можно написать ( Z — Y ) = 2b и (Z + Y )=2a. Решая их относительно Z и Y, получим Z = (a + b) и Y = (a — b). Тогда можно записать, что X = 4ab и, подставляя эти значения в
. Так как Z и Y нечетные числа, значит можно написать ( Z — Y ) = 2b и (Z + Y )=2a. Решая их относительно Z и Y, получим Z = (a + b) и Y = (a — b). Тогда можно записать, что X = 4ab и, подставляя эти значения в 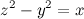 (1), получим
(1), получим 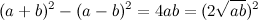 .
.Примечание
Чтобы избежать получения подобных треугольников, и, учитывая, что Z и Y — нечетные числа по условию, числа a и b должны быть взаимно простыми и разной четности. Далее будем считать, что четным является число a. Для того, чтобы упорядочить распределение прямоугольных треугольников в множестве натуральных чисел N, поступим следующим образом: из этого множества вычтем все числа, которые являются четными степенями натуральных чисел. Обозначим это множество
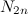 , где n — натуральное число. Затем из оставшихся натуральных чисел вычтем все числа, которые являются нечетными (≥3) степенями натуральных чисел и обозначим множество этих чисел как
, где n — натуральное число. Затем из оставшихся натуральных чисел вычтем все числа, которые являются нечетными (≥3) степенями натуральных чисел и обозначим множество этих чисел как 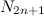 . Оставшиеся натуральные числа составят множество, числа которого есть натуральные числа в первой степени. Обозначим это множество
. Оставшиеся натуральные числа составят множество, числа которого есть натуральные числа в первой степени. Обозначим это множество 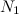 . Очевидно, соединение этих 3-х множеств есть множество натуральных чисел, или
. Очевидно, соединение этих 3-х множеств есть множество натуральных чисел, или 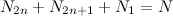 . Множество
. Множество 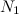 представим как ряд
представим как ряд 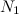 = {1, 2, 3, 5, 6, 7, 10, 11, 12, 13, 14, 15, 17,………}. Представим множества
= {1, 2, 3, 5, 6, 7, 10, 11, 12, 13, 14, 15, 17,………}. Представим множества 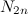 и
и 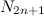 в виде рядов. Тогда множество
в виде рядов. Тогда множество 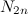 будет представлять собой матрицу, состоящую из бесконечного числа строк, каждая строка будет состоять из чисел ряда
будет представлять собой матрицу, состоящую из бесконечного числа строк, каждая строка будет состоять из чисел ряда 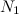 , возведенных в степень 2n, а n — есть номер строки. Так первая строка состоит из квадратов всех чисел ряда
, возведенных в степень 2n, а n — есть номер строки. Так первая строка состоит из квадратов всех чисел ряда 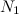 , вторая строка состоит из 4-х степеней этих чисел и т.д. Рассмотрим множество
, вторая строка состоит из 4-х степеней этих чисел и т.д. Рассмотрим множество 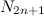 , которое будет представлять собой матрицу, состоящую из бесконечного числа строк, каждая строка которой будет состоять из чисел ряда
, которое будет представлять собой матрицу, состоящую из бесконечного числа строк, каждая строка которой будет состоять из чисел ряда 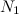 , возведенных в степень 2n+1. (n — есть номер строки). Так первая строка этой матрицы состоит из кубов чисел ряда
, возведенных в степень 2n+1. (n — есть номер строки). Так первая строка этой матрицы состоит из кубов чисел ряда 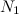 , вторая строка состоит из чисел ряда
, вторая строка состоит из чисел ряда 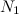 в пятой степени и т.д. Рассмотрим множество
в пятой степени и т.д. Рассмотрим множество 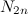 . Т.к.
. Т.к. 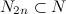 , то примем тот же алгоритм построения треугольников (см. выше). Найдем «генераторы» тождества, Это будут числа
, то примем тот же алгоритм построения треугольников (см. выше). Найдем «генераторы» тождества, Это будут числа 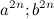 , где
, где 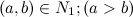 , составим тождество:
, составим тождество: 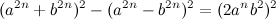 (3), мы получили множество прямоугольных треугольников с целочисленными сторонами. Здесь
(3), мы получили множество прямоугольных треугольников с целочисленными сторонами. Здесь 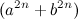 — гипотенуза,
— гипотенуза, 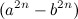 — катет и
— катет и 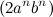 — второй катет. Для опровержения утверждения Ферма нужно, чтобы стороны X, Y, Z искомого треугольника равнялись
— второй катет. Для опровержения утверждения Ферма нужно, чтобы стороны X, Y, Z искомого треугольника равнялись 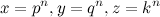 (4). Где (p, q, k, n) — натуральные числа. По теореме Пифагора будем иметь
(4). Где (p, q, k, n) — натуральные числа. По теореме Пифагора будем иметь 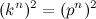 или
или 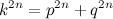 и утверждение Ферма будет опровергнуто. Из тождества
и утверждение Ферма будет опровергнуто. Из тождества 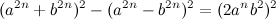 видно, что
видно, что 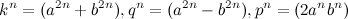 . Рассмотрим последнее равенство
. Рассмотрим последнее равенство 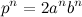 , в этом равенстве «p» ни при каких значениях «a и b»
, в этом равенстве «p» ни при каких значениях «a и b» 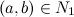 не будет натуральным числом, если
не будет натуральным числом, если 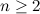 . Это означает, что в рассмотренном множестве треугольников не существует ни одного треугольника с искомыми сторонами (4).
. Это означает, что в рассмотренном множестве треугольников не существует ни одного треугольника с искомыми сторонами (4).Теперь рассмотрим множество
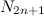 . Обозначим (2n+1) как «m», тогда во множестве
. Обозначим (2n+1) как «m», тогда во множестве 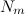 получим прямоугольные треугольники, описываемые тождеством
получим прямоугольные треугольники, описываемые тождеством 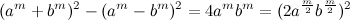 (6). Если мы сможем построить прямоугольный треугольник X, Y, Z со сторонами
(6). Если мы сможем построить прямоугольный треугольник X, Y, Z со сторонами 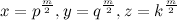 (7), где
(7), где 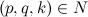 , то мы опровергнем утверждение Ферма, т.к. по теореме Пифагора
, то мы опровергнем утверждение Ферма, т.к. по теореме Пифагора 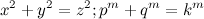 и (p, q и k) — натуральные числа. Надо, чтобы
и (p, q и k) — натуральные числа. Надо, чтобы 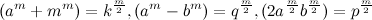 . Рассматривая последнее равенство заметим, что «p» не может быть натуральным числом ни при каких значениях «a и b»,
. Рассматривая последнее равенство заметим, что «p» не может быть натуральным числом ни при каких значениях «a и b», 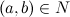 , если
, если 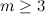 . Значит и в этом множестве треугольников не существует ни одного треугольника с искомыми сторонами (7).
. Значит и в этом множестве треугольников не существует ни одного треугольника с искомыми сторонами (7).Однако из вышесказанного видно, что все доказательство сводится к анализу числа
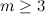
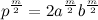 , где «
, где «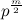 » при любых натуральных «a и b» не будет натуральным числом в степени «m/2». Или же
» при любых натуральных «a и b» не будет натуральным числом в степени «m/2». Или же 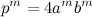 (8) при тех же условиях не будет натуральным числом в степени «m». Из доказательства видно, что «генераторами» тождества (6) являются числа «
(8) при тех же условиях не будет натуральным числом в степени «m». Из доказательства видно, что «генераторами» тождества (6) являются числа «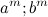 » из ряда
» из ряда 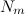 Но, анализируя
Но, анализируя 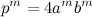 (8), можно подставить вместо «
(8), можно подставить вместо «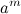 » число
» число 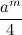 . Так как
. Так как 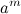 есть четное число, (см.Примечание), то
есть четное число, (см.Примечание), то 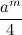 — натуральное число. После подстановки его в (8) получим
— натуральное число. После подстановки его в (8) получим 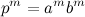 , то есть натуральные числа в степени «m». Совершив вышеуказанную подстановку в тождество (6), и, обозначив
, то есть натуральные числа в степени «m». Совершив вышеуказанную подстановку в тождество (6), и, обозначив 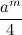 через
через 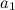 , получим следующее тождество:
, получим следующее тождество: 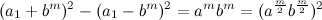 . Мы получили множество прямоугольных треугольников со сторонами
. Мы получили множество прямоугольных треугольников со сторонами 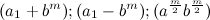 . Если ( k,q, p) — натуральные числа в нечетной степени, т.е.
. Если ( k,q, p) — натуральные числа в нечетной степени, т.е. 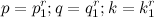 где r — любое нечетное число, а
где r — любое нечетное число, а 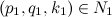 . Чтобы опровергнуть Ферма нужно, чтобы:
. Чтобы опровергнуть Ферма нужно, чтобы: 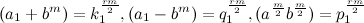 В последнем равенстве при любых натуральных a и b,
В последнем равенстве при любых натуральных a и b, 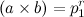 — числа натуральные, но первые два равенства невозможны, так как, если «m и r» любые нечетные числа, то
— числа натуральные, но первые два равенства невозможны, так как, если «m и r» любые нечетные числа, то 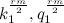 — иррациональные числа, а числа в скобках — числа натуральные. Если же (k,q, p) — натуральные числа в четной степени, т.е.
— иррациональные числа, а числа в скобках — числа натуральные. Если же (k,q, p) — натуральные числа в четной степени, т.е. 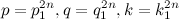 , то мы получим следующие равенства
, то мы получим следующие равенства 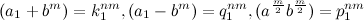 (5). В данном варианте последнее равенство невозможно, т.к. извлекая корень m степени из обеих частей равенства получим
(5). В данном варианте последнее равенство невозможно, т.к. извлекая корень m степени из обеих частей равенства получим 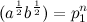 , т.е. в скобках иррациональное число, а
, т.е. в скобках иррациональное число, а 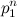 — натуральное. Это значит, что и в этом множестве не найдено «нужного» треугольника. А это значит, что для любых нечетных «m» утверждение Ферма верно, а значит, верно, для всех простых показателей «m ≥ 3».
— натуральное. Это значит, что и в этом множестве не найдено «нужного» треугольника. А это значит, что для любых нечетных «m» утверждение Ферма верно, а значит, верно, для всех простых показателей «m ≥ 3». Остается найти доказательство теоремы для четных показателей. Из (5) следует, что, если в каноническом разложении четного показателя степени есть нечетное простое число, то утверждение Ферма для этой степени верно. Очевидно, что этому условию отвечают все четные числа, кроме числа «4» и чисел кратных четырем, т.е. 8, 16, 32, 64 … и т.д. В разложении этих чисел есть только простое число 2. Поэтому вышеприведенное доказательство не дает ответа для этих степеней.
Значит остается доказать теорему для «n = 4». Можно предположить, что у Ферма было общее доказательство, но не полное. Может быть, поэтому он и не записал свое доказательство. И только через несколько лет, создав свой метод «бесконечного или неопределенного спуска», он доказал, что не существует прямоугольного треугольника с целочисленными сторонами, у которого площадь равнялась бы квадрату натурального числа. После этого доказательство теоремы для «n = 4» не составило труда. Это доказательство Ферма записал. И теорема оказалась доказанной полностью.