Девять лет назад я посещал курс физики в колледже, и мой профессор рассказал одну вещь, которая поразила меня. Я думаю, не будет преувеличением сказать, что это одно из наиболее широко используемых математических открытий — от оптики до квантовой физики, радиоастрономии, сжатия MP3 и JPEG, рентгеновской кристаллографии, распознавания голоса и МРТ. Этот математический инструмент называется преобразование Фурье, в честь французского физика и математика 18-го века Жозефа Фурье. Им пользовались даже Джеймс Уотсон и Фрэнсис Крик, чтобы декодировать структуру двойной спирали ДНК из рентгенограмм, произведенных Розалиндой Франклин. (Крик был экспертом по преобразованиям Фурье, он в шутку назвал свою книгу «Преобразования Фурье для орнитологов», чтобы объяснить суть Уотсону, заядлому любителю птиц).
Вы наверняка пользуетесь идеей Фурье каждый день, если слушаете MP3, смотрите картинки в Интернете, задаете вопрос Siri или ловите радиостанцию. (Фурье, кстати, очень любил работать. В дополнение к своей работе в области теоретической физики и математики, он также стал первым, кто открыл парниковый эффект [pdf ].)
Так в чем заключается открытие Фурье и почему оно так полезно? Представьте себе ноту на фортепиано. При нажатии клавиши фортепиано молоток ударяет по струне, которая вибрирует с определенной частотой (нота Ля — 440 раз в секунду). Пока струна вибрирует, молекулы воздуха вокруг нее двигаются взад и вперед, создавая волну из молекул, которую мы называем звуком. Если бы вы могли наблюдать за движением воздуха, то увидели бы гладкую, волнистую, бесконечно повторяющуюся кривую, которая называется синусоидой. (Пояснение: В примере с клавишей фортепиано на самом деле возникнет больше одной синусоиды. Богатство настоящих нот фортепиано заключено в большом количестве мягких обертонов, которые появляются в дополнение к основной синусоидальной волне. Нота приблизительно равна синусоиде, но при помощи камертона можно получить звук, который состоит из одной синусоиды).

Звуковую волну ноты можно рассматривать как простую синусоидальную волну. Milan B на Shuttershock
Теперь нажмите на три клавиши вместе, чтобы получить аккорд. Полученная звуковая волна получится не такой аккуратной – она будет более беспорядочной. Но в этой кривой звуковой волне скрыт простой рисунок. Ведь аккорд мы получили, нажав всего на три клавиши, так что эта звуковая волна состоит из трех нот (или синусоид ).
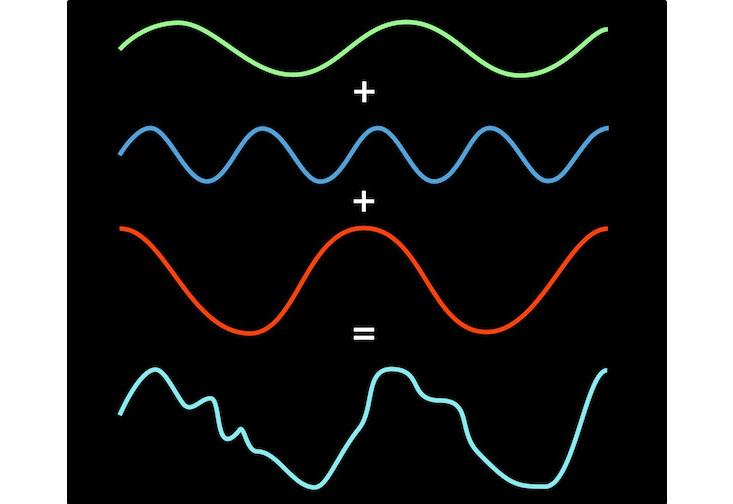
Звуковая волна, полученная с помощью аккорда фортепиано, может выглядеть беспорядочно, но это всего лишь сумма трех разных нот. Christine Daniloff / MIT
Фурье догадался, что это не просто особое свойство музыкальных аккордов, оно применимо в более общем виде к любой повторяющейся волне, квадратной, круглой, волнистой, треугольной, в общем – к любой. Преобразование Фурье похоже на математическую призму — вы подаете волну, а оно показывает ее составные части, то есть ноты (или синусоиды), которые при соединении воссоздадут волну.
Если это звучит немного абстрактно, вот несколько методов визуализации трюка Фурье. Здесь мы встречаем Лукаса В. Барбосу, бразильского студента-физика, который безвозмездно создает невероятные математические и научные анимации для Википедии под ником LucasVB.
Итак, давайте посмотрим на квадратную волну, пропущенную через призму Фурье, и увидим, что получилось на выходе.
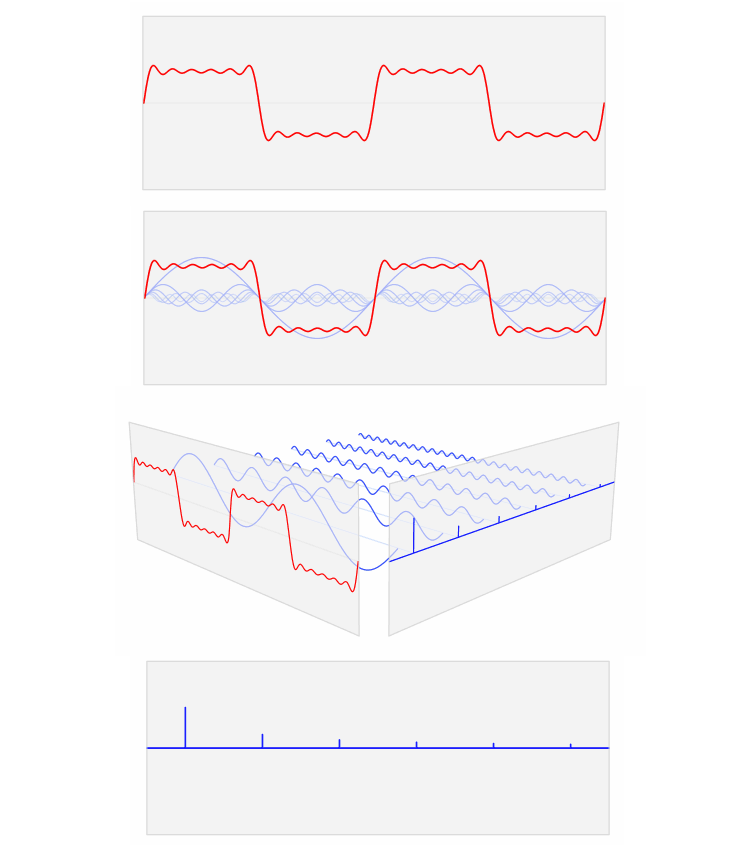
Кадры из анимации LucasVB
На этих картинках (по ссылке выше можно увидеть анимацию целиком) красная квадратная волна конвертируется в набор нот (синие синусоидальные волны). Синие волны – это математические ингредиенты красной волны. По этой же аналогии преобразование Фурье является рецептом, который точно укажет, сколько и какой ноты нужно смешать вместе, чтобы восстановить исходную волну. Вертикальные синие линии в анимации – это график, визуально представляющий количество каждой ноты.
Вот немного другой подход, представленный Мэтью Хендерсоном или «Matthen», студентом Кембриджского университета, который также создает анимации интересных математических фишек. Matthen объясняет трюк Фурье, используя круги вместо синусоид. На помощь ему приходит набор кругов различных размеров, центр каждого из которых находится на границе большего круга. Круги начинают вращаться, маленькие движутся вокруг больших и делают это быстрее. Если проследить движение одной точки на наименьшей окружности, можно реконструировать волну любой формы, как показано на анимации и на картинке. Опять же, преобразование Фурье говорит нам, как построить волну: какие круги и скорости использовать.

Matthew Henderson
Если вы застали спирограф, то идея отслеживания сложных моделей с помощью окружностей внутри окружностей может показаться вам знакомой. Вот это интерактивная версия анимации, похожей на созданную LucasVB, где можно развлекаться и изменять размеры кругов.
В общем, преобразование Фурье говорит нам, сколько каждого ингредиента «ноты» (синусоидальной волны или круга) содержится в общей волне. А вот почему это полезно. Представьте, что вы говорите со своим другом по телефону и хотите, чтобы он нарисовал эту квадратную волну. Можно использовать утомительный способ и зачитать длинный список цифр, которые показывают высоту волны в каждый момент времени. Учтя все эти цифры, ваш друг сможет создать исходную волну. Так работали старые аудио форматы, например, WAV. Но если ваш друг разбирается в преобразованиях Фурье, можно сделать все проще: вы можете просто назвать несколько чисел — размеров кругов на картинке выше. Эти круги можно использовать, чтобы восстановить исходную волну.
Это не какой-то сложный математический фокус. Преобразование Фурье используется почти везде, где есть волны. Вездесущий MP3 формат использует вариант трюка Фурье для достижения огромного сжатия по сравнению с файлами WAV (произносится как «вейв»), которые были до него. MP3 разбивает песню на короткие сегменты. В каждом сегменте преобразование Фурье разбивает аудио волну на составляющие ноты, которые хранятся вместо исходной волны. Преобразование Фурье также говорит нам, сколько и какой ноты используется в песне, чтобы знать, какие ноты важны. Очень высокие ноты не так важны (наши уши едва слышат их), поэтому МР3 выбрасывает их, добиваясь еще большего сжатия данных. Поэтому меломанам не нравится МР3 — это не lossless формат аудио, и они утверждают, что могут услышать разницу.
Приложение Shazam именно так распознает песни. Оно разбивает песню на куски, а затем использует преобразование Фурье, чтобы определить ноты, из которых состоит каждый кусок. Затем оно выполняет поиск по базе данных, чтобы проверить, похож ли этот «отпечаток» нот на какие-нибудь хранящиеся песни. Распознавание речи использует ту же идею, чтобы сравнить ноты в вашем голосе со списком известных слов.
Вы можете использовать преобразование Фурье для изображений. Вот отличное видео, которое показывает, как можно нарисовать лицо Гомера Симпсона с помощью кругов. Онлайн-энциклопедия Wolfram Alpha использует подобную идею, чтобы рисовать лица известных людей. Следующий факт пригодится, чтобы блеснуть знаниями на вечеринке: преобразование Фурье также используется для сжатия изображений в формат JPEG. В старые добрые времена Microsoft Paint изображения сохранялись в формате BMP, которые представляли собой длинный список чисел, кодирующих цвет каждого пикселя. JPEG – это MP3 изображений. Чтобы создать JPEG, надо разделить изображение на мелкие квадраты 8 на 8 пикселей. Чтобы воссоздать изображение, для каждой части нужно применить ту же идею круга, который рисует лицо Гомера Симпсона. Так же, как МР3 отбрасывает очень высокие ноты, JPEG отбрасывает очень маленькие круги. В результате мы получаем огромное уменьшение размера файла при небольшой потере качества, этот фокус подарил нам онлайн мир, который мы все любим (и благодаря которому у нас появились гифки с котиками).

Randall Munroe / XKCD
Как преобразование Фурье используются в науке? Через Твиттер я попросил ученых описать, как идеи Фурье помогли им в своей работе. Ответ поразил меня. Откликнувшиеся ученые использовали преобразование Фурье для изучения колебаний погружаемых конструкций, взаимодействующих с жидкостями, для предсказывания землетрясений, для определения составных частей очень далеких галактик, для поиска новых физических процессов в тепловых остатках Большого Взрыва, для определения структуры белков, для анализа цифровых сигналов НАСА, для изучения акустики музыкальных инструментов, для уточнения модели круговорота воды, для поиска пульсаров (вращающихся нейтронных звезд) и для определения структуры молекул с помощью ядерного магнитного резонанса. Преобразование Фурье даже использовалось для определения фальшивых картин Джексона Поллока через распознавание химических веществ в краске.
Вот так! Немало для одного математического фокуса.
Аатиш Бхатиа недавно получил степень кандидата физических наук в университете Принстона, занимаясь популяризацией науки и инженерии. Он — автор признанного блога Empirical Zeal, аккаунт в твитере — @aatishb.
Вы наверняка пользуетесь идеей Фурье каждый день, если слушаете MP3, смотрите картинки в Интернете, задаете вопрос Siri или ловите радиостанцию. (Фурье, кстати, очень любил работать. В дополнение к своей работе в области теоретической физики и математики, он также стал первым, кто открыл парниковый эффект [pdf ].)
Так в чем заключается открытие Фурье и почему оно так полезно? Представьте себе ноту на фортепиано. При нажатии клавиши фортепиано молоток ударяет по струне, которая вибрирует с определенной частотой (нота Ля — 440 раз в секунду). Пока струна вибрирует, молекулы воздуха вокруг нее двигаются взад и вперед, создавая волну из молекул, которую мы называем звуком. Если бы вы могли наблюдать за движением воздуха, то увидели бы гладкую, волнистую, бесконечно повторяющуюся кривую, которая называется синусоидой. (Пояснение: В примере с клавишей фортепиано на самом деле возникнет больше одной синусоиды. Богатство настоящих нот фортепиано заключено в большом количестве мягких обертонов, которые появляются в дополнение к основной синусоидальной волне. Нота приблизительно равна синусоиде, но при помощи камертона можно получить звук, который состоит из одной синусоиды).
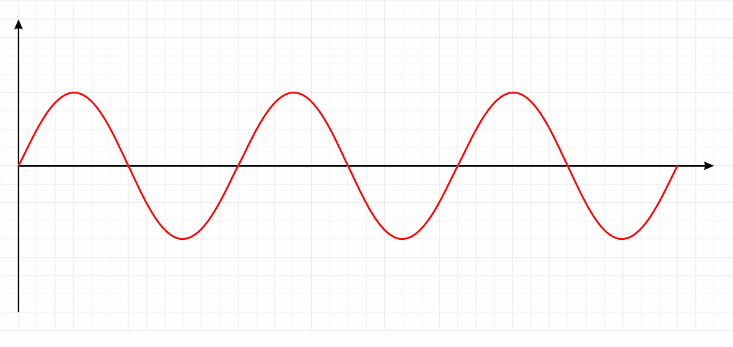
Звуковую волну ноты можно рассматривать как простую синусоидальную волну. Milan B на Shuttershock
Теперь нажмите на три клавиши вместе, чтобы получить аккорд. Полученная звуковая волна получится не такой аккуратной – она будет более беспорядочной. Но в этой кривой звуковой волне скрыт простой рисунок. Ведь аккорд мы получили, нажав всего на три клавиши, так что эта звуковая волна состоит из трех нот (или синусоид ).
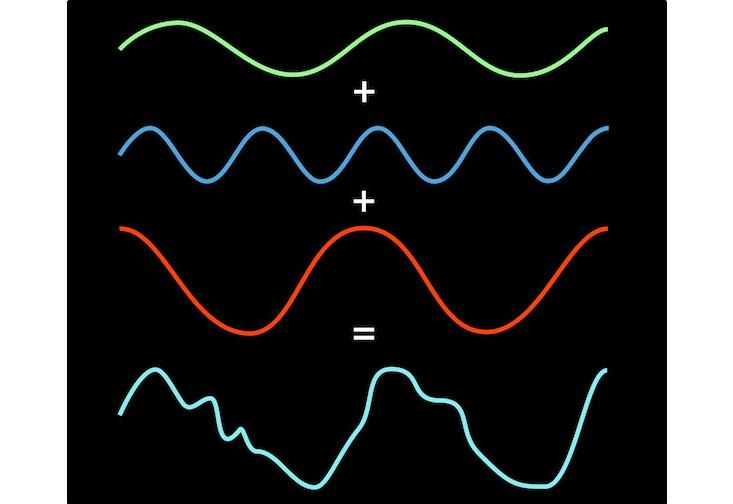
Звуковая волна, полученная с помощью аккорда фортепиано, может выглядеть беспорядочно, но это всего лишь сумма трех разных нот. Christine Daniloff / MIT
Фурье догадался, что это не просто особое свойство музыкальных аккордов, оно применимо в более общем виде к любой повторяющейся волне, квадратной, круглой, волнистой, треугольной, в общем – к любой. Преобразование Фурье похоже на математическую призму — вы подаете волну, а оно показывает ее составные части, то есть ноты (или синусоиды), которые при соединении воссоздадут волну.
Если это звучит немного абстрактно, вот несколько методов визуализации трюка Фурье. Здесь мы встречаем Лукаса В. Барбосу, бразильского студента-физика, который безвозмездно создает невероятные математические и научные анимации для Википедии под ником LucasVB.
Итак, давайте посмотрим на квадратную волну, пропущенную через призму Фурье, и увидим, что получилось на выходе.

Кадры из анимации LucasVB
На этих картинках (по ссылке выше можно увидеть анимацию целиком) красная квадратная волна конвертируется в набор нот (синие синусоидальные волны). Синие волны – это математические ингредиенты красной волны. По этой же аналогии преобразование Фурье является рецептом, который точно укажет, сколько и какой ноты нужно смешать вместе, чтобы восстановить исходную волну. Вертикальные синие линии в анимации – это график, визуально представляющий количество каждой ноты.
Вот немного другой подход, представленный Мэтью Хендерсоном или «Matthen», студентом Кембриджского университета, который также создает анимации интересных математических фишек. Matthen объясняет трюк Фурье, используя круги вместо синусоид. На помощь ему приходит набор кругов различных размеров, центр каждого из которых находится на границе большего круга. Круги начинают вращаться, маленькие движутся вокруг больших и делают это быстрее. Если проследить движение одной точки на наименьшей окружности, можно реконструировать волну любой формы, как показано на анимации и на картинке. Опять же, преобразование Фурье говорит нам, как построить волну: какие круги и скорости использовать.
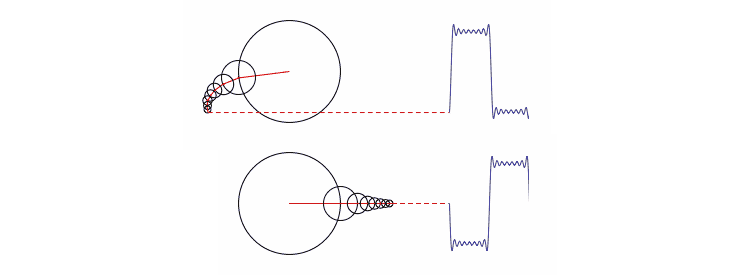
Matthew Henderson
Если вы застали спирограф, то идея отслеживания сложных моделей с помощью окружностей внутри окружностей может показаться вам знакомой. Вот это интерактивная версия анимации, похожей на созданную LucasVB, где можно развлекаться и изменять размеры кругов.
В общем, преобразование Фурье говорит нам, сколько каждого ингредиента «ноты» (синусоидальной волны или круга) содержится в общей волне. А вот почему это полезно. Представьте, что вы говорите со своим другом по телефону и хотите, чтобы он нарисовал эту квадратную волну. Можно использовать утомительный способ и зачитать длинный список цифр, которые показывают высоту волны в каждый момент времени. Учтя все эти цифры, ваш друг сможет создать исходную волну. Так работали старые аудио форматы, например, WAV. Но если ваш друг разбирается в преобразованиях Фурье, можно сделать все проще: вы можете просто назвать несколько чисел — размеров кругов на картинке выше. Эти круги можно использовать, чтобы восстановить исходную волну.
Это не какой-то сложный математический фокус. Преобразование Фурье используется почти везде, где есть волны. Вездесущий MP3 формат использует вариант трюка Фурье для достижения огромного сжатия по сравнению с файлами WAV (произносится как «вейв»), которые были до него. MP3 разбивает песню на короткие сегменты. В каждом сегменте преобразование Фурье разбивает аудио волну на составляющие ноты, которые хранятся вместо исходной волны. Преобразование Фурье также говорит нам, сколько и какой ноты используется в песне, чтобы знать, какие ноты важны. Очень высокие ноты не так важны (наши уши едва слышат их), поэтому МР3 выбрасывает их, добиваясь еще большего сжатия данных. Поэтому меломанам не нравится МР3 — это не lossless формат аудио, и они утверждают, что могут услышать разницу.
Приложение Shazam именно так распознает песни. Оно разбивает песню на куски, а затем использует преобразование Фурье, чтобы определить ноты, из которых состоит каждый кусок. Затем оно выполняет поиск по базе данных, чтобы проверить, похож ли этот «отпечаток» нот на какие-нибудь хранящиеся песни. Распознавание речи использует ту же идею, чтобы сравнить ноты в вашем голосе со списком известных слов.
Вы можете использовать преобразование Фурье для изображений. Вот отличное видео, которое показывает, как можно нарисовать лицо Гомера Симпсона с помощью кругов. Онлайн-энциклопедия Wolfram Alpha использует подобную идею, чтобы рисовать лица известных людей. Следующий факт пригодится, чтобы блеснуть знаниями на вечеринке: преобразование Фурье также используется для сжатия изображений в формат JPEG. В старые добрые времена Microsoft Paint изображения сохранялись в формате BMP, которые представляли собой длинный список чисел, кодирующих цвет каждого пикселя. JPEG – это MP3 изображений. Чтобы создать JPEG, надо разделить изображение на мелкие квадраты 8 на 8 пикселей. Чтобы воссоздать изображение, для каждой части нужно применить ту же идею круга, который рисует лицо Гомера Симпсона. Так же, как МР3 отбрасывает очень высокие ноты, JPEG отбрасывает очень маленькие круги. В результате мы получаем огромное уменьшение размера файла при небольшой потере качества, этот фокус подарил нам онлайн мир, который мы все любим (и благодаря которому у нас появились гифки с котиками).

Randall Munroe / XKCD
Как преобразование Фурье используются в науке? Через Твиттер я попросил ученых описать, как идеи Фурье помогли им в своей работе. Ответ поразил меня. Откликнувшиеся ученые использовали преобразование Фурье для изучения колебаний погружаемых конструкций, взаимодействующих с жидкостями, для предсказывания землетрясений, для определения составных частей очень далеких галактик, для поиска новых физических процессов в тепловых остатках Большого Взрыва, для определения структуры белков, для анализа цифровых сигналов НАСА, для изучения акустики музыкальных инструментов, для уточнения модели круговорота воды, для поиска пульсаров (вращающихся нейтронных звезд) и для определения структуры молекул с помощью ядерного магнитного резонанса. Преобразование Фурье даже использовалось для определения фальшивых картин Джексона Поллока через распознавание химических веществ в краске.
Вот так! Немало для одного математического фокуса.
Аатиш Бхатиа недавно получил степень кандидата физических наук в университете Принстона, занимаясь популяризацией науки и инженерии. Он — автор признанного блога Empirical Zeal, аккаунт в твитере — @aatishb.