
Как известно, последняя революция в криптографии случилась в 1976 году из-за статьи “New Directions in Cryptography” американских ученых Уитфилда Диффи (Whitfield Diffie) и Мартина Хеллмана (Martin Hellman). Эта работа оказалась для последующего развития криптографии как «Большой Взрыв» — произошло рождение новой вселенной асимметричной криптографии. До этого момента (во всяком случае в открытой печати) существовала только симметричная криптография. Молодыми и никому тогда не известными учеными впервые была предложена схема, в которой для выработки общего секрета абонентам изначально не надо было обмениваться какими-либо секретными ключами. Помимо своей первозданности этот алгоритм интересен тем, что несмотря на то, что могут устаревать “сложные” задачи, лежащие в основе его безопасности, их можно успешно заменять новыми. Изначально это была задача дискретного логарифмирования в мультипликативной группе конечного поля (Discrete Logarithm Problem, сокр. — DLP), сейчас на практике широко используется задача дискретного логарифмирования в группе точек эллиптической кривой (Elliptic Curve DLP — ECDLP). В будущем (не таком уж далеком) предполагается использовать другие “сложные” задачи, которые будет иметь экспоненциальную сложность не только на классическом, но и на квантовом компьютере. Они называются постквантовыми. Одной из таких задач является задача нахождения изогении между эллиптическими кривыми, о которой я хочу рассказать в этой статье.
Поскольку цель статьи – максимально просто объяснить новый математический “движок” для протокола Диффи-Хеллмана (Diffie-Hellman или сокращенно — DH), то не рассматриваются некоторые атаки: мы предполагаем, что злоумышленник может только читать сообщения в канале, но не может вмешиваться в работу канала, чтобы перехватывать сообщения абонентов и отправлять свои (т.е. злоумышленник не “Человек посередине”). На практике (к примеру, в протоколе TLS) на открытые ключи DH может ставиться подпись и тут уже Человек Посередине подменить ключ DH не может: от сервера клиенту открытый ключ DH приходит как сертификат, от клиента к серверу – временный (ephemeral) ключ, подписанный на постоянном закрытом ключе ЭЦП клиента. В общем, в суровой реальности от подмены открытых ключей DH спасает технология PKI, основанная на доверии обеих сторон одному УЦ. Но, опять же, чтобы не отвлекать читателя от главного – математики, про PKI я ничего не пишу в этой статье. И еще раз: поскольку известны случаи, когда реализовывались и внедрялись системы, в которых стороны обменивались временными (ephemeral) открытыми ключами, которые стороны никак не проверяли (видимо те, кто их проектировал считали себя слишком занятыми людьми, чтобы изучить основы криптографии или хотя бы обратиться к специалистам), то прошу не забывать, что в реальной жизни это необходимо. Человек Посередине (он же Посредник, он же Man-in-the-middle) – это не Снежный Человек и он существует.
Прошлое: классический Диффи-Хеллман
Алиса и Боб изначально выбирают параметры (domain parameters): мультипликативную группу конечного поля и g — генератор ее подгруппы. Ничего страшного в слове генератор нет. Это всего лишь один из элементов группы со следующим свойством: если взять его степени от 1 до числа элементов группы, мы получим всю группу целиком. Подгруппа – это подмножество группы, которая сама по себе – тоже группа (при перемножении ее элементов в любых сочетаниях, мы получим только элементы этого самого подмножества).
Пример:
Элементы группы:
числа от 1 до p — 1, где p – простое число.
Групповая операция a*b mod p: умножаем элементы группы a и b, затем a*b делим на p. Остаток от деления a*b на p и есть результат операции a*b mod p.
К примеру, пусть модуль p равен 11. Чаще всего обозначается как . Состоит из 11 – 1 = 10 элементов: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Число элементов в группе называется порядком группы (group order). Порядок равен 10.
А теперь немного поиграем с операциями:
5*6 mod 11 = 8,
1*10 mod 11 = 10.
1 для этой группы – это нейтральный элемент. Neutral — т.к. он “не взаимодействует” ни с какими другими элементами и результат операции с ним всегда равен второму элементу операции. В данном случае 1*10 mod 11 — это 10.
6*2 mod 11 = 1.
Для любого элемента любой группы существует обратный элемент, который “обращает” его в нейтральный. Для этой группы 6 и 2 – обратные друг для друга.
Когда групповая операция называется умножением (как в случае ), то используют такие обозначения для обратного к
элемента:
Т.е.
*
= 1 Что еще можно сказать про эту группу? Она коммутативна (или абелева):
Генераторы группы — это такие ее элементы, все степени которых являются всеми элементами группы. Группы, в которых есть хотя бы один такой элемент называют циклическими. Как понять, что x – генератор? Самый примитивный метод: построить таблицу степеней x:
Как насчет степеней 2?
2*2 mod 11 = 4
4*2 mod 11 = 8
8*2 mod 11 = 5
5*2 mod 11 = 10
10*2 mod 11 = 9
9*2 mod 11 = 7
7*2 mod 11 = 3
3*2 mod 11 = 6
6*2 mod 11 = 1 — мы видим, что цикл замкнулся. Степени 2 генерируют всю группу
Итого: 2 — генератор .
Порядок элемента – минимальная степень, в которую его надо возвести, чтобы получить нейтральный. Порядок 2 в равен 10.
Теперь рассмотрим степени 3:
3*3 mod 11 = 9
9*3 mod 11 = 5
5*3 mod 11 = 4
4*3 mod 11 = 1
Порядок 3 равен 5. Он не “пробегает” все значения , т.к. мы видим, что на пятой степени происходит зацикливание: если продолжить умножение, то опять получим 3, 9, 5, 4, 1.
Что еще можно сказать про 3?
Это тоже генератор. Но не для
Легко видеть, что это подмножество -подгруппа: есть нейтральный элемент 1. Замкнутость: результат любых a*b mod p для этих чисел не выходит за пределы этого множества, ведь результат будет одним из множества {3, 9, 5, 4, 1}.
Каждый элемент имеет обратный: 3*4 mod 11 = 1, 9*5 mod 11 = 1, 1*1 mod 11 = 1. Какие еще подгруппы есть в ?
Еще есть группа порядка 2: {1, 10}
Ну и конечно же тривиальные подгруппы { 1 } и {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} (т.к. формально группа является подгруппой самой себя)
Как можно оптимизировать поиск генератора для ?
Тут необходимо использовать фундамент теории групп – теорему Лагранжа: “Порядок подгруппы делит порядок группы”.
Элемент x либо является генератором группы, либо является генератором одной из ее подгрупп. Следовательно, возведение x в степени порядков подгрупп и сравнение результата с 1 может это подтвердить или опровергнуть.
Вернемся к
Таким образом мы могли бы сократить вычисления для 2, возведя его только в степени 2 и 5!
Аналогично для 4:
4*4 mod 11 = 5 ≠1 ok, следующий шаг считаем пятую степень для 4:
Порядок 18 = 3*3*2. Делители 18: 2, 3, 6, 9 Выбираем случайный элемент, например 3:
Возводим 3 в степень r1 = 18/3 = 6:
Возводим 3 в степень r2 = 18/2 = 9:
Совершенно не обязательно возводить исследуемый элемент в степени всех подгрупп т.е. 2, 3, 6, 9, т.к. если элемент окажется генератором подгруппы подгруппы, то все равно возведение в степень порядка подгруппы даст 1.
К примеру, если бы мы выбрали не 3, а 11, то остановились бы на первом шаге:
т.к. 11 имеет порядок 3
3 в
Нетривиальные подгруппы
Но вернемся к DH. На практике это выбор параметров для него – это выбор большого ( ~
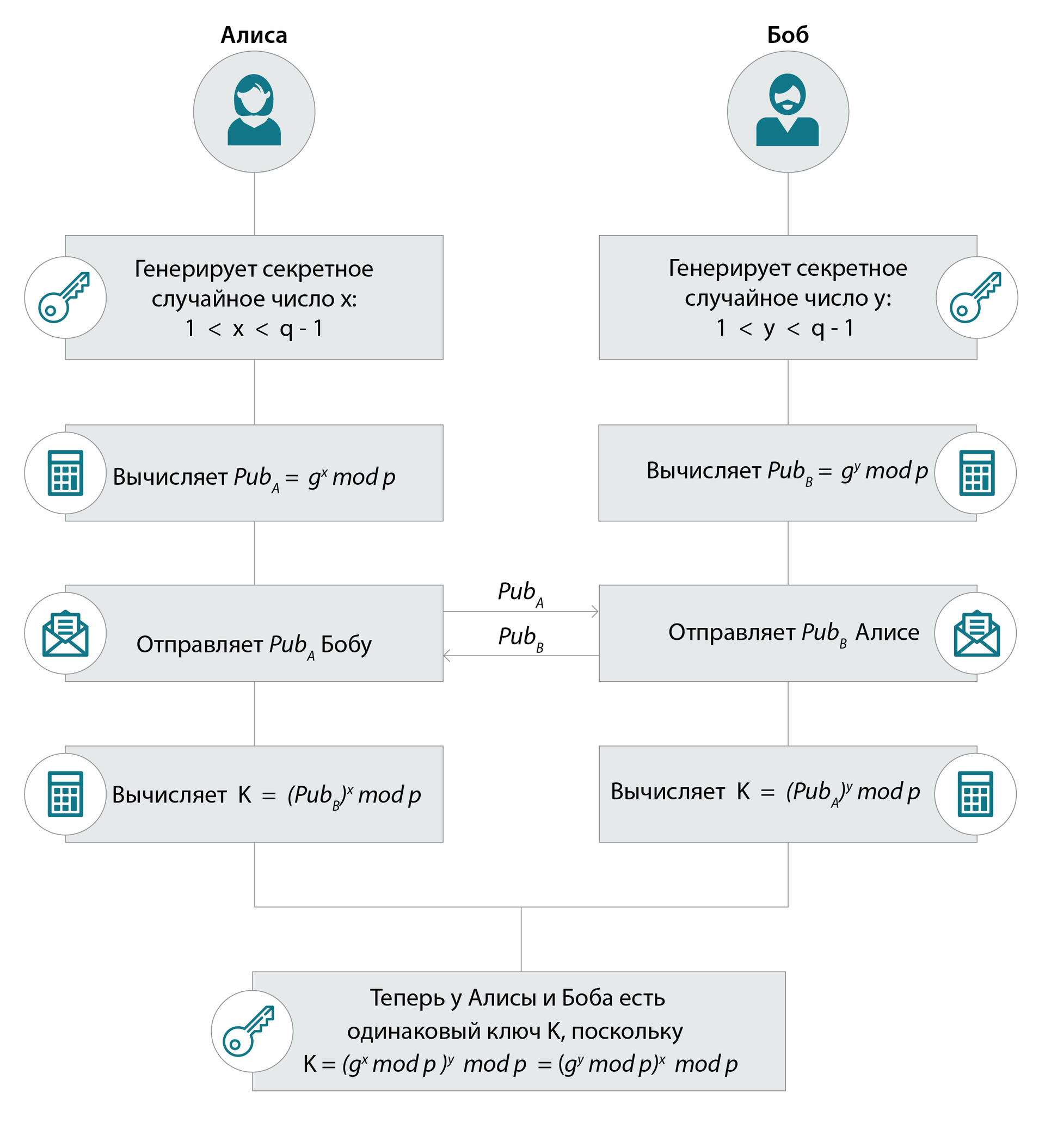
Примечание: Алисе и Бобу необходимо проверять приходящие извне ключи на принадлежность их “рабочей” подгруппе большого простого порядка q:
Алиса проверяет mod p = 1? Если нет, то протокол прерывается.
Аналогично поступает Боб: он проверяет ключ, пришедший от Алисы: mod p = 1?
Мы сейчас не рассматриваем противника, который мог бы подменить по дороге открытые ключи, но тем не менее всегда надо помнить, что и в криптографии встречаются случаи из разряда “при таких друзьях нам и враги не нужны”: программа на устройствах Алисы или Боба может содержать различные ошибки (в реализации модульной арифметики, или просто может повредиться память).
Если проверки прошли нормально, то Алиса и Боб считают ключи для симметричных алгоритмов, чтобы уже с их помощью защищать канал передачи данных (например шифровать данные и считать MAC (Message Autentication Code) или просто считать MAC).
Обратная к
Выбором группы занимаются конечно же не лично Алиса или Боб, а криптографы (хотя, некоторое подмножество всех Алис и Бобов принадлежит к их множеству, но мы не рассматриваем этот частный случай). Подмножество криптографов, которые глубоко разбираются в строении групп и знают, какие из них использовать безопасно иногда публикуют результаты своей работы в виде конкретных чисел p ,g и пошаговых описаний алгоритмов с тестовыми векторами. Их можно найти в виде стандартов NIST или RFC.
Вот пример небезопасных параметров для DH: группа “гладкого” порядка, т.е. у которой число элементов можно представить в виде произведения степеней небольших простых чисел, т.к. в ней можно легко вычислить дискретный логарифм с помощью метода Поллига-Хеллмана, который вычисляет дискретный логарифм в подгруппах группы, а потом с помощью китайской теоремы об остатках получает логарифм для самой группы. Поскольку вычисления по китайской теореме сами по себе достаточно просты, то сложность всего алгоритма Поллига-Хеллмана можно приблизительно оценить, как сложность вычисления DL в самой большой из подгрупп простого порядка.
Настоящее: эллиптический Диффи-Хеллман
В 1985 году Нил Коблиц (Neal I. Koblitz) и Виктор Миллер (Victor Saul Miller) независимо друг от друга изобрели, как можно использовать эллиптические кривые в криптографии. Их открытие помогло создать эллиптические варианты алгоритмов Диффи-Хеллмана, Эль-Гамаля, MQV, DSS, ГОСТ Р 34.10-94, которые изначально использовали мультипликативную группу конечного поля. В результате новые алгоритмы (за исключением ГОСТ) получили префикс EC: ECDH, EC ElGamal, ECMQV, ECDSS. А наш российский ГОСТ Р 34.10-94 трансформировался в ГОСТ Р 34.10-2001 (а потом в более надежный 34.10-2012). Зачем был нужен такой переход к эллиптическим кривым? Он позволил проводить более быстрые вычисления при том же уровне безопасности.
Алиса и Боб выбирают Доменные параметры (domain parameters) для эллиптических кривых.
Из чего состоят Доменные параметры для эллиптических кривых:
1. Поле Галуа GF(
характеристика поля (простое число)
(На практике чаще используют n = 1. Обозначается GF(
простым полем (prime field). Его элементы — все числа от 0 до p-1)
2. Уравнение Вейерштрасса кривой над полем GF(
все коэффициенты (в данном случае A и B) и решения (x и y) – элементы поля):
где A и B такие, что 4
координаты
3. Порядок группы точек (число всех ее элементов)
Обозначается как #E(GF(
Представляется как q*k, где q (большое простое число) – порядок подгруппы, а k – маленькое
число (не обязательно простое) называется cofactor (сомножитель)
4. Генератор подгруппы группы точек кривой (base point): точка Q, имеющая порядок q. (Алгоритм дискретного логарифмирования Поллига-Хеллмана применим также и к группе точек эллиптической кривой, как и к любой другой абелевой группе, поэтому группа точек должна иметь “негладкий” порядок. Т.е. равный произведению большого простого числа на маленькое число. В отличие от классического варианте, группа которого всегда содержит p-1 элемент, группа эллиптических кривых могут иметь и простой порядок)
Напомним самое основное:
Элементы группы — это точки кривой, т.е. пары (x, y) — решения уравнения Вейерштрасса. Групповая операция называется сложением точек:
(x1, y1) + (x2, y2) = (x3, y3)
Плюс еще есть так называемая Точка На Бесконечности (Point At Infinity) или нулевая точка (но точка на бесконечности – звучит красивее, согласитесь) Обозначим ее O. Это аналог единицы для мультипликативной группы конечного поля (из классического DH): 1*t mod p = t*1 mod p = t, для кривых: (x, y) + O= O + (x, y) = (x, y). Ее принципиальное отличие от сестры из мультипликативной группы заключается в том, что ее нельзя представить в виде каких-либо элементов поля, т.е. как обычную точку (x, y) так, чтобы можно было проводить с ней вычисления как с остальными точками по общей формуле.
В первой части статьи мы будем рассматривать только простое поле GF(p), поэтому все примеры и формулы используют суффикс mod p:
Формула сложения точек (X1, Y1) и (X2, Y2):
X3 =
Y3 = µ(X1 — X3) — Y1 mod p
где µ= (Y2-Y1)/(X2-X1) mod p, если X1 ≠ X2:
Если же X1 = X2 и Y1 = Y2 ≠ 0, то µ= (3
В случае, когда X1 = X2 и Y1 = — Y2 mod p, то формулы неприменимы и результат – точка на бесконечности.
Дроби помогают красивее выразить обратный элемент в мультипликативной группе: к примеру,
Обозначим скалярное произведение числа n на точку Q так: [n]*Q.
[n]*Q = Q + Q + … + Q + Q
n раз (это последовательная проделанная n раз операция сложения с помощью приведенных выше формул) Злоумышленник знает доменные параметры: кривую и точку Q (генератор подгруппы) а также результат умножения скаляра n на точку Q: [n]*Q. Что он хочет найти: число n (т.е решить задачу ECDLP). В каком случае это легко? Капитан Очевидность говорит, что если Q принадлежит подгруппе небольшого размера, то точка [n]*Q будет принадлежать той же самой подгруппе и злоумышленник будет перебирать все возможные скаляры и умножать их на Q, пока не получит известную ему точку [n]*Q. Поэтому Q должна принадлежать подгруппе большого простого порядка.
Итак, основная группа должна содержать подгруппу большого простого порядка (иными словами порядок всей группы должен быть НЕ гладким). Капитан Очевидность снова в деле и сообщает: чтобы группа могла содержать большую подгруппу, необходимо, чтобы сама группа была большой. Порядок группы точек кривой E над полем GF(
#E(GF(
Теперь мы знаем, как число элементов поля связано с числом точек: они практически не отличается по порядку. Можно ли утверждать, что для злоумышленнику необходимо порядка точек кривой вычислений для получения скаляра? Для “брутфорса” – да, но ведь есть более красивый метод, который требует гораздо меньше усилий. Метод Полларда, который также применим и для DLP (как и к любой другой коммутативной группе). Это вероятностный алгоритм. Число операций, которые он требует — около квадратного корня из числа элементов группы. Таким образом, если мы рассматриваем “боевые” криптографические кривые (c q*k, где q большое простое число, а k – маленькое число: на практике 1, 2 или 4 ) то их безопасность удобно оценивать как число операций, которое должен выполнить злоумышленник при помощи самого «продвинутого» метода для этих кривых – метода Полларда.
Пример:
Наиболее часто используемая в мире кривая NIST P-256 над простым полем.
Структура ее группы такая: порядок равен большому простому числу. Т.е порядок равен q*k, где q – простое, а cofactor k = 1. Ее безопасность можно оценить как
Помимо кривых с гладким порядком есть и другие, которые позволяют относительно легко решить ECDLP: суперсингулярные (со следом Фробениуса t таким, что: t mod p = 0) и аномальные ( t = 1 ). Предположим, что кривая Боба и Алиса не попадает ни в одну из этих плохих компаний и поэтому практически решить ECDLP для нее невозможно.
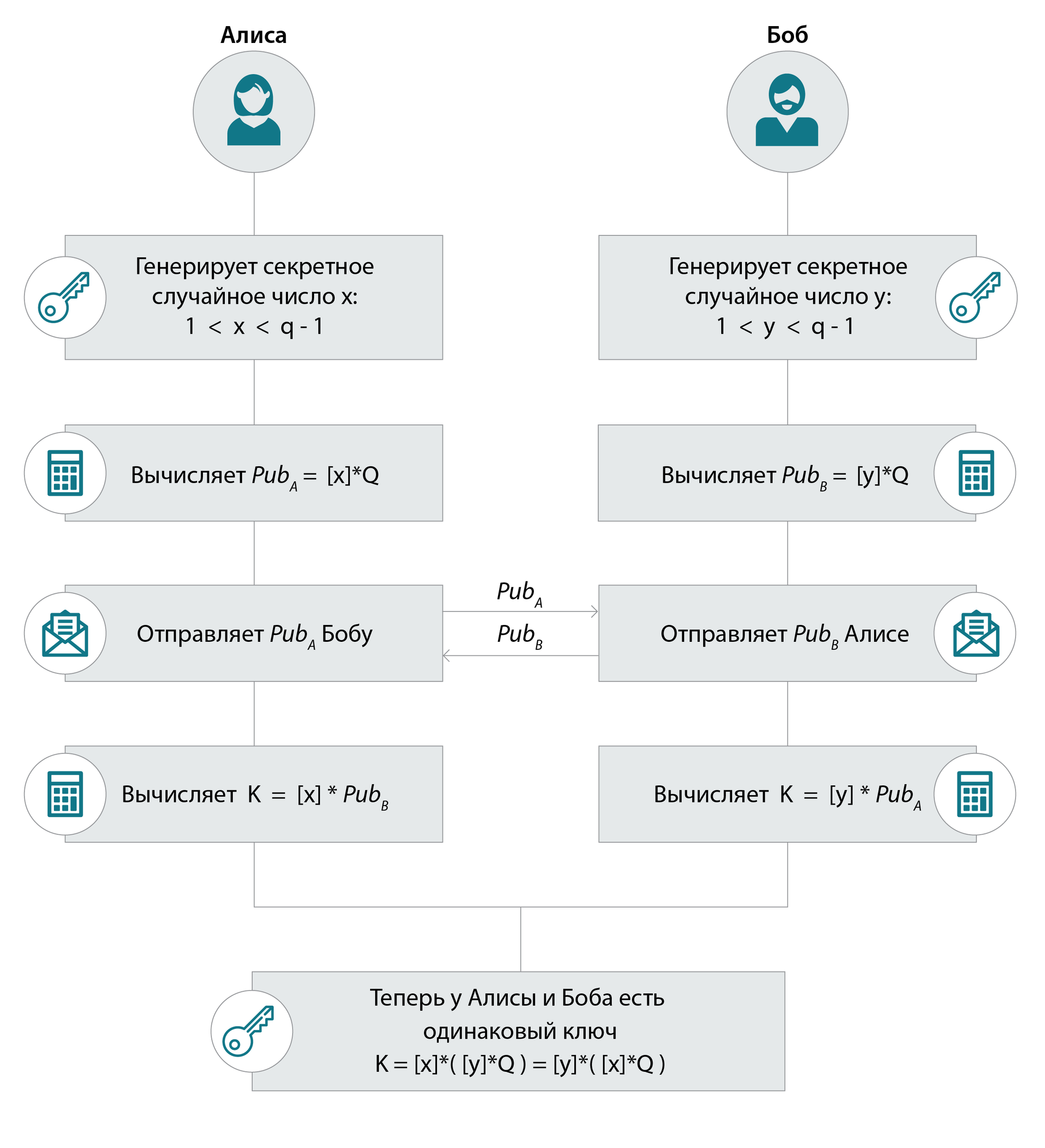
Примечание: как и в случае с классическим DH, хорошим тоном считается проверка всех (входящих и исходящих) точек на принадлежность к группе, но тут ситуация немножко сложнее. Сначала координаты подставляются в уравнение – это проверка на вхождение в группу. Потом для проверки на принадлежность большой подгруппе порядка q мы умножаем точку на q. Если в результате получаем точку на бесконечности, то все OK, а если нет — точка лежит в какой-то другой подгруппе и протокол должен быть прерван.
Итого:
Классический DH: в результате обмена ключами у Алисы и Боба появляется одинаковый элемент группы: ее генератор, умноженный на себя x*y раз:
А теперь сopypaste:
Эллиптический DH: в результате обмена ключами у Алисы и Боба появляется одинаковый элемент группы: ее генератор — точка Q, сложенная с собой x*y раз: [x*y]*Q
Разница в названии операций для данных групп (сложение или умножение) не важна (ведь у группы только есть только одна операция). Так что теперь более попробуем более универсально:
в результате обмена ключами у Алисы и Боба появляется одинаковый элемент группы: ее генератор, над которым была проведена x*y раз групповая операция с ним же.
Квантовый кошмар и ненависть
Классический и эллиптический DH помимо математического изящества объединяет один неприятный факт: сложные (для обычных компьютеров) задачи ECDLP и DLP, лежащие в их основе могут быть легко решены, если будут созданы квантовые компьютеры, которые способны удержать в связанном состоянии достаточно большое число кубит (от нескольких сотен до нескольких тысяч). Кроме того, это означает конец для криптосистемы RSA: квантовый алгоритм Шора позволяет разлагать большие числа на простые множители за полиномиальное время. Поэтому именно для асимметричных алгоритмов постквантовая тема очень актуальна. Для симметричных шифров все пока не так ужасно – их будут атаковать квантовым алгоритмом Гровера, который имеет сложность квадратный корень из мощности множества ключа. К примеру, если вы использовали AES c длиной ключа 128 бит, то чтобы сохранить тот же уровень безопасности нужен тот же AES, но c 256 битным ключом (а AES-128 падает до 64 битного уровня, т.е. атакующему нужно будет выполнить
Одной из самых перспективных сложных математических задач, устойчивых к квантовым компьютерам являются изогении эллиптических кривых. Про про них читайте в продолжении.
Литература:
Брюс Шнайер, Нильс Фергюссон “Практическая криптография”
Alfred J. Menezes, Paul C. van Oorschot and Scott A. Vanstone “Handbook of Applied Cryptography”
Lawrence C. Washington “Elliptic Curves: Number Theory and Cryptography, Second Edition”