В предыдущих постах мы рассказывали о том, как разрабатывается и тестируется САПР КОМПАС-3D. Дополнительно запущен цикл статей по разработке приложений с использованием API КОМПАС-3D. Пришло время рассказать о «начинке», которая управляет всеми построениями в КОМПАСе – ядре геометрического моделирования C3D или просто геометрическом ядре C3D.
Автолестница пожарная АЛ-30 (изготовитель: ООО «Пожарные Системы»)
Наличие в CAD-системе интерфейса прикладного программирования API позволяет расширять возможности системы проектирования и способствует значительному сокращению времени разработки дополнительных программных компонентов к уже имеющейся на предприятии САПР. Это достигается за счёт использования готового набора функций, представленных в удобной и понятной для разработчика форме. Как правило, внутренняя реализация таких функций скрыта от программиста-пользователя API и представляет собой объект интеллектуальной собственности обладателя исходных кодов программного обеспечения.
Особенности работы с интерфейсом прикладного программирования прописываются в технической документации. Здесь же указывается, какие значения необходимо подавать на вход конкретной функции, чтобы получить на выходе корректные значения согласно предназначению данной функции. То есть API позволяет абстрагироваться от реализации отдельных программных блоков при разработке приложений:

Работа с API-интерфейсом по принципу «чёрного ящика»
Благодаря наличию в КОМПАС-3D собственного API базовая функциональность системы с течением времени была дополнена приложениями для проектирования радиоэлектронной аппаратуры и электрооборудования, деталей машин, трубопроводов, металлоконструкций, зданий и сооружений различного назначения.
Но использовать API САПР не всегда удобно и целесообразно. Дело в том, что при обращении к геометрическим функциям ядра напрямую разработчик избавляется от необходимости взаимодействия с промежуточными звеньями CAD-системы, такими как графический интерфейс, спецификации и пр. Поэтому одинаковая геометрия в ядре создаётся быстрее, чем в API САПР. Также использование геометрического ядра позволяет разработчикам инженерных приложений сохранять в секрете придуманные ими ноу-хау. Например, особенности построения сложных геометрических моделей могут быть легко скрыты от внимания пользователя.
Большинство современных САПР базируются на дереве построения 3D-модели, а значит каждая новая операция приводит к перестроению всего дерева, поэтому с помощью ядра намного проще проводить итерационные построения, в частности создание зубчатых передач:

Коническая передача, построенная приложением «Shaft» без использования геометрического ядра: множественные операции построения скрыты в макроэлементе
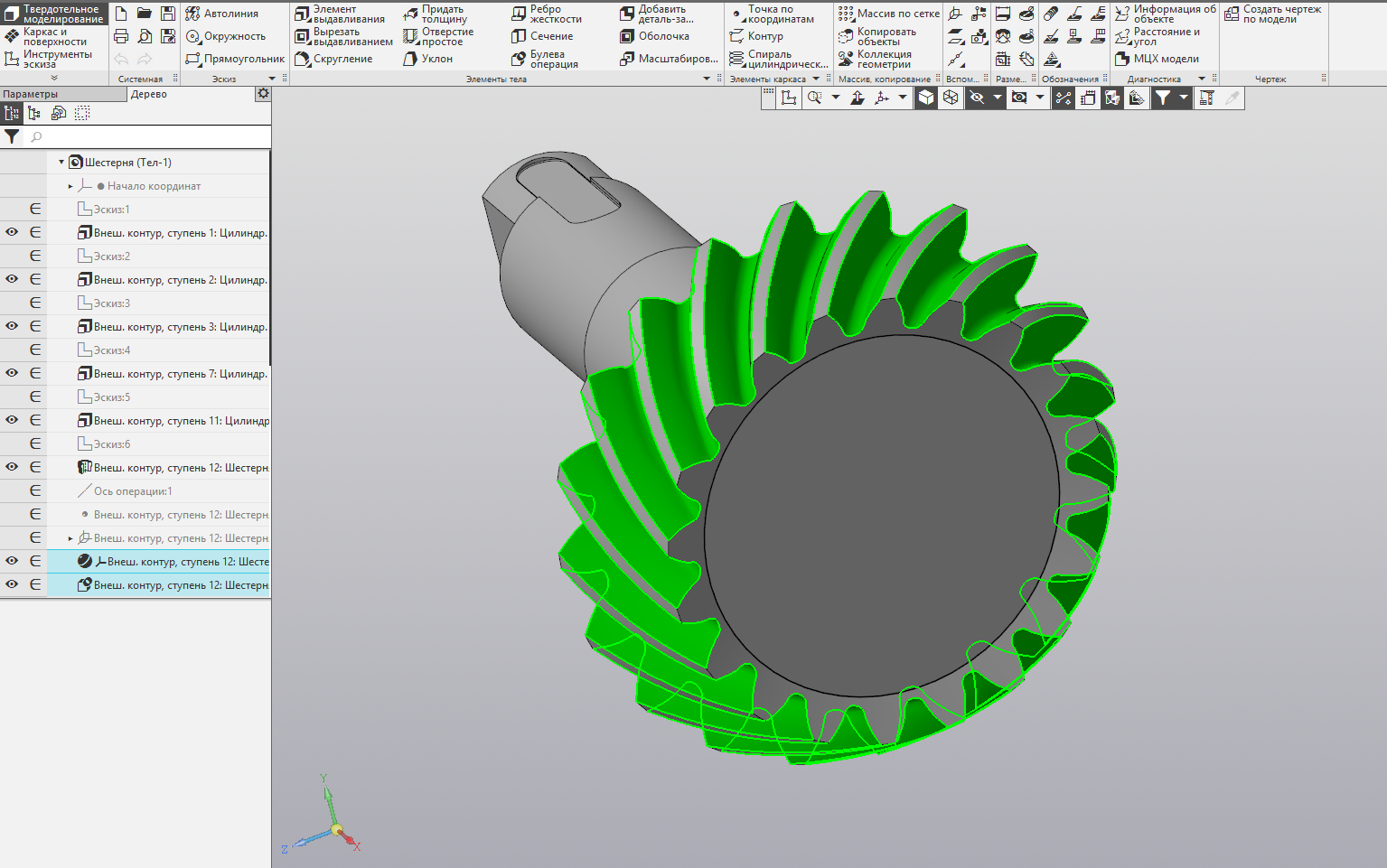
Коническая передача, построенная приложением «Валы и механические передачи» с использованием функциональности геометрического ядра: для построения зубчатого венца требуется всего две операции (Картинка кликабельна)
В случае с приложением «Валы и механические передачи» использование ядра позволяет разработчикам:
В общем случае, с применением в разработке геометрического ядра уменьшается вероятность поломки модели при смене пользователем версии приложения, да и в целом повышается стабильность работы программы при непредсказуемых действиях пользователей. А включение математической библиотеки в основу разрабатываемого решения позволяет обеспечить независимость от существующих программ. Как минимум, это означает, что не нужно тянуть за проектом дистрибутив сторонней (часто тяжелой) системы и производить лицензионные отчисления за использования связанной САПР. Тем не менее, последнее утверждение нельзя считать весомым аргументом, так как разработчики приложений часто ориентируется на аудиторию конкретной CAD, CAM или CAE системы, иногда достигающей значения в десятки и сотни тысяч активных пользователей.
Набор геометрических функций в САПР образует в совокупности геометрическое ядро системы, которое отличается от игрового движка с реалистичной 3D-графикой. Наиболее наглядно это демонстрируется через аналогию с графическими редакторами. Как известно, часть из них работает с растровой графикой, основанной на точках. Другие редакторы оперируют векторной графикой, которая базируется на кривых линиях. Точно также в 3D-приложениях существует полигональная графика, которая основывается на положении точек в пространстве (из них строятся полигоны), и сплайновая графика, представляющая собой сочетание математических формул и уравнений.
Выражаясь в терминах САПР, можно сказать, что полигональная графика строится на фасетном представлении геометрии. Такое же представление используется в игровых движках и в различных анимационных пакетах для создания спецэффектов кино:
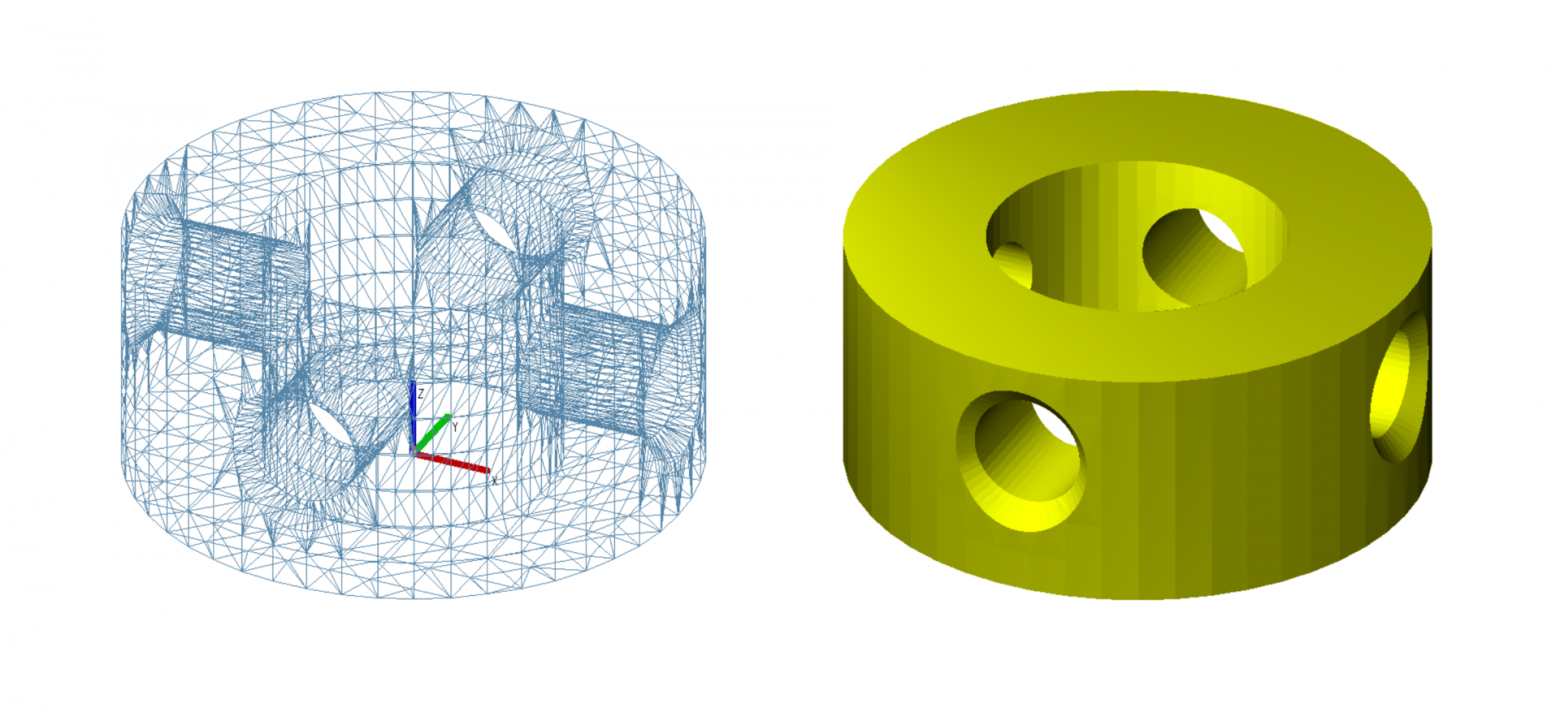
Фасетное представление геометрии 3D-модели
Математически точное описание 3D-модели задаётся граничным представлением. Его основная особенность в том, что для представления формы геометрической модели используется набор граней, проходящих по границе, которая отделяет внутреннее пространство моделируемого объекта от остальной части пространства. Как вы уже, наверное, догадались – именно это представление используется в геометрических ядрах.

Граничное представление геометрии 3D-модели
Можно выделить три основных причины:
Масштабируемость.
Точность отображения модели в граничном представлении определяется на уровне САПР, а расчёт полигональных сеток производится таким образом, чтобы модель визуально казалась гладкой. При этом, если мы возьмём исходную полигональную модель, то, вне зависимости от выбранной системы проектирования, при увеличении масштаба мы сперва увидим увеличивающиеся треугольники, а затем модель станет угловатой. Ограничение в этом случае задаётся на уровне самой модели — с какой точностью изначально была рассчитана сетка, например, при записи в формат STL, с такой точностью и придется работать дальше.

Охотничье хозяйство в натуральный размер. При увеличении модели все грани сохраняют форму (Картинка кликабельна)
Гладкость.

Пример передачи фасетной модели в чертёж. Видно как сливаются места сгущения сетки (Картинка кликабельна)
Точность.

Обработка модели в CAM-системе Esprit
В действительности же причин значительно больше, но это – профессиональные тонкости.
Невероятно, но факт: современные системы проектирования (и КОМПАС-3D – не исключение) работают с двумя представлениями геометрии. Граничное представление используются в процессе моделирования, после чего производится расчёт триангуляционной сетки и строится полигональная модель, которая затем отправляется в видеокарту для отрисовки визуальной сцены. На данном этапе в процесс может вмешаться ядро визуализации, например C3D Vision, которое отвечает за управление отрисовкой модели с использованием средств математической, программной и аппаратной оптимизации. Подробнее об этом мы расскажем в следующих статьях.
Каждый разработчик инженерного программного обеспечения рано или поздно оказывается перед выбором: писать ли необходимые математические алгоритмы самому или приобрести готовые компоненты на стороне? В истории АСКОН использование сторонних модулей рассматривалось в 1995 году, когда обсуждалась разработка КОМПАС-3D. Тогда был выбран тернистый пусть самостоятельного написания геометрических функций, в основе которых лежит довольно сложная математика. Подробнее ознакомиться с ней можно, прочитав книгу Николая Голованова по геометрическому моделированию:


Оглавление и обложка книги «Геометрическое моделирование» Н.Н. Голованова (Картинки кликабельны)
Мало кто знает, что позднее, в 2000-х годах, в АСКОН повторно рассматривался вопрос использования стороннего математического ядра для работы с 3D. Было произведено тестирование доступных на рынке CAD-компонентов и принято стратегически важное решение о продолжении разработки собственного геометрического ядра. Оно получило имя C3D, что является сокращением от внутрикорпоративного названия проекта «Core3D». Сегодня это ядро успешно используется не только внутри АСКОН, но и в проектах других разработчиков систем автоматизированного проектирования в России и за рубежом.
Вторая часть статьи

Аркадий Камнев
Менеджер по маркетингу в C3D Labs
Автолестница пожарная АЛ-30 (изготовитель: ООО «Пожарные Системы»)
Зачем нужно геометрическое ядро, когда имеется доступ к API CAD-системы?
Наличие в CAD-системе интерфейса прикладного программирования API позволяет расширять возможности системы проектирования и способствует значительному сокращению времени разработки дополнительных программных компонентов к уже имеющейся на предприятии САПР. Это достигается за счёт использования готового набора функций, представленных в удобной и понятной для разработчика форме. Как правило, внутренняя реализация таких функций скрыта от программиста-пользователя API и представляет собой объект интеллектуальной собственности обладателя исходных кодов программного обеспечения.
Особенности работы с интерфейсом прикладного программирования прописываются в технической документации. Здесь же указывается, какие значения необходимо подавать на вход конкретной функции, чтобы получить на выходе корректные значения согласно предназначению данной функции. То есть API позволяет абстрагироваться от реализации отдельных программных блоков при разработке приложений:

Работа с API-интерфейсом по принципу «чёрного ящика»
Благодаря наличию в КОМПАС-3D собственного API базовая функциональность системы с течением времени была дополнена приложениями для проектирования радиоэлектронной аппаратуры и электрооборудования, деталей машин, трубопроводов, металлоконструкций, зданий и сооружений различного назначения.
Но использовать API САПР не всегда удобно и целесообразно. Дело в том, что при обращении к геометрическим функциям ядра напрямую разработчик избавляется от необходимости взаимодействия с промежуточными звеньями CAD-системы, такими как графический интерфейс, спецификации и пр. Поэтому одинаковая геометрия в ядре создаётся быстрее, чем в API САПР. Также использование геометрического ядра позволяет разработчикам инженерных приложений сохранять в секрете придуманные ими ноу-хау. Например, особенности построения сложных геометрических моделей могут быть легко скрыты от внимания пользователя.
Большинство современных САПР базируются на дереве построения 3D-модели, а значит каждая новая операция приводит к перестроению всего дерева, поэтому с помощью ядра намного проще проводить итерационные построения, в частности создание зубчатых передач:

Коническая передача, построенная приложением «Shaft» без использования геометрического ядра: множественные операции построения скрыты в макроэлементе
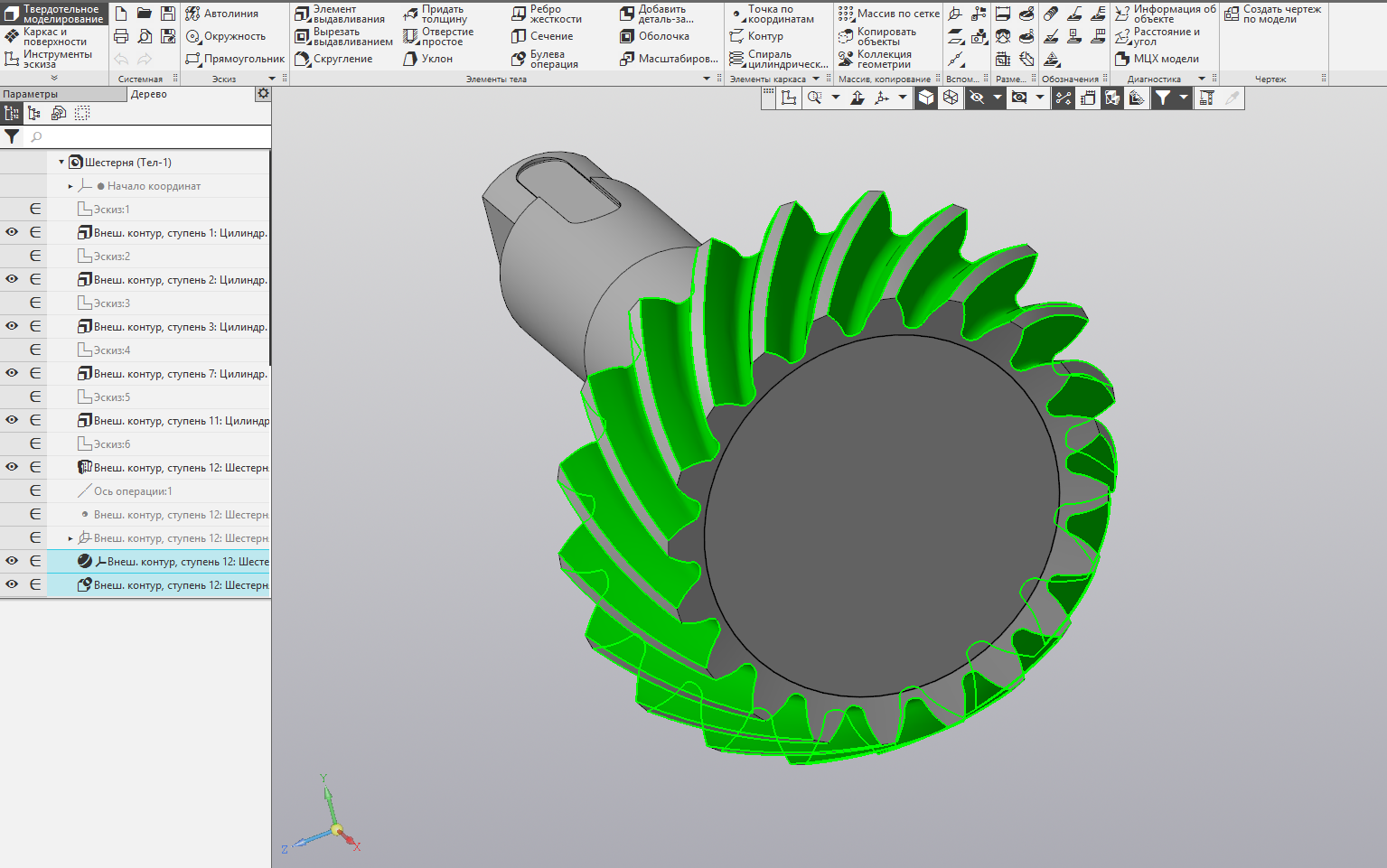
Коническая передача, построенная приложением «Валы и механические передачи» с использованием функциональности геометрического ядра: для построения зубчатого венца требуется всего две операции (Картинка кликабельна)
В случае с приложением «Валы и механические передачи» использование ядра позволяет разработчикам:
- сократить время создания трёхмерной геометрии;
- увеличить точность расчётов сложно формируемых моделей;
- автоматически проводить замеры измерительных размеров передач, а также выполнять невидимые глазу построения, необходимые для расчетов передач.
В общем случае, с применением в разработке геометрического ядра уменьшается вероятность поломки модели при смене пользователем версии приложения, да и в целом повышается стабильность работы программы при непредсказуемых действиях пользователей. А включение математической библиотеки в основу разрабатываемого решения позволяет обеспечить независимость от существующих программ. Как минимум, это означает, что не нужно тянуть за проектом дистрибутив сторонней (часто тяжелой) системы и производить лицензионные отчисления за использования связанной САПР. Тем не менее, последнее утверждение нельзя считать весомым аргументом, так как разработчики приложений часто ориентируется на аудиторию конкретной CAD, CAM или CAE системы, иногда достигающей значения в десятки и сотни тысяч активных пользователей.
Геометрические и игровые ядра
Набор геометрических функций в САПР образует в совокупности геометрическое ядро системы, которое отличается от игрового движка с реалистичной 3D-графикой. Наиболее наглядно это демонстрируется через аналогию с графическими редакторами. Как известно, часть из них работает с растровой графикой, основанной на точках. Другие редакторы оперируют векторной графикой, которая базируется на кривых линиях. Точно также в 3D-приложениях существует полигональная графика, которая основывается на положении точек в пространстве (из них строятся полигоны), и сплайновая графика, представляющая собой сочетание математических формул и уравнений.
Выражаясь в терминах САПР, можно сказать, что полигональная графика строится на фасетном представлении геометрии. Такое же представление используется в игровых движках и в различных анимационных пакетах для создания спецэффектов кино:

Фасетное представление геометрии 3D-модели
Математически точное описание 3D-модели задаётся граничным представлением. Его основная особенность в том, что для представления формы геометрической модели используется набор граней, проходящих по границе, которая отделяет внутреннее пространство моделируемого объекта от остальной части пространства. Как вы уже, наверное, догадались – именно это представление используется в геометрических ядрах.
Пояснение.
В граничном представлении на основе NURBS кривые и поверхности точно проходят по заданным дискретным местам пространства (точкам или кривым), в остальных точках пространства к ним предъявляется требование гладкости. Так как исходные данные для построения NURBS объектов являются дискретными, то NURBS кривые и поверхности в граничном представлении считаются точными, потому что они точно соответствуют исходным требованиям. Более того, NURBS объектами можно точно представить форму почти всех аналитических кривых и поверхностей.
Всё, для чего известны аналитические законы, в граничном представлении описывается другими объектами, например, кривыми и поверхностями второго порядка. Для объектов, которые не поддаются аналитическому описанию, граничное представление использует специальные приёмы. Так, для точного описания кривой пересечения двух кубических NURBS поверхностей применяются итерационные методы: кривая пересечения представляется набором точек, которые служат начальными приближениями для определения положения точки кривой пересечения с требуемой точностью. Таким образом, положение точек кривой пересечения при каждом обращении к кривой насчитывается заново итерационными методами по лежащей в кривой информации.
UPD: Общение человека с кривой пересечения, к примеру двух NURBS поверхностей, происходит следующим образом: человек сообщает кривой пресечения значение параметра, а кривая выдает точку в пространстве, соответствующую этому параметру. То есть в кривой пересечения лежит некоторая информация (это не обязательно множество точек, могут лежать пересекаемые поверхности и некоторые данные о параметре кривой), которая позволяет рассчитать точку на пересечении поверхностей с максимальной машинной точностью, выше которой не имеет смысла уточнять. Соответственно, кусочно-линейных представлений, кубических кривых, аппроксимационных кривых в кривой пересечения нет. Кривая пересечения поверхностей — это объект, который для указанного параметра выдает точку в пространстве.
Всё, для чего известны аналитические законы, в граничном представлении описывается другими объектами, например, кривыми и поверхностями второго порядка. Для объектов, которые не поддаются аналитическому описанию, граничное представление использует специальные приёмы. Так, для точного описания кривой пересечения двух кубических NURBS поверхностей применяются итерационные методы: кривая пересечения представляется набором точек, которые служат начальными приближениями для определения положения точки кривой пересечения с требуемой точностью. Таким образом, положение точек кривой пересечения при каждом обращении к кривой насчитывается заново итерационными методами по лежащей в кривой информации.
UPD: Общение человека с кривой пересечения, к примеру двух NURBS поверхностей, происходит следующим образом: человек сообщает кривой пресечения значение параметра, а кривая выдает точку в пространстве, соответствующую этому параметру. То есть в кривой пересечения лежит некоторая информация (это не обязательно множество точек, могут лежать пересекаемые поверхности и некоторые данные о параметре кривой), которая позволяет рассчитать точку на пересечении поверхностей с максимальной машинной точностью, выше которой не имеет смысла уточнять. Соответственно, кусочно-линейных представлений, кубических кривых, аппроксимационных кривых в кривой пересечения нет. Кривая пересечения поверхностей — это объект, который для указанного параметра выдает точку в пространстве.

Граничное представление геометрии 3D-модели
Но тогда почему для геометрического ядра не подходит полигональная графика?
Можно выделить три основных причины:
Масштабируемость.
Любой объект необходимо беспрепятственно увеличивать и уменьшать. Дефекты геометрии неуместны.
Имеется ввиду, что при любом масштабе визуальной сцены изображение будет настолько гладким, насколько гладкая сама модель. Круглое всегда остаётся круглым, угол — углом. Нарушение изложенного принципа подразумевает наличие дефектов.
Точность отображения модели в граничном представлении определяется на уровне САПР, а расчёт полигональных сеток производится таким образом, чтобы модель визуально казалась гладкой. При этом, если мы возьмём исходную полигональную модель, то, вне зависимости от выбранной системы проектирования, при увеличении масштаба мы сперва увидим увеличивающиеся треугольники, а затем модель станет угловатой. Ограничение в этом случае задаётся на уровне самой модели — с какой точностью изначально была рассчитана сетка, например, при записи в формат STL, с такой точностью и придется работать дальше.
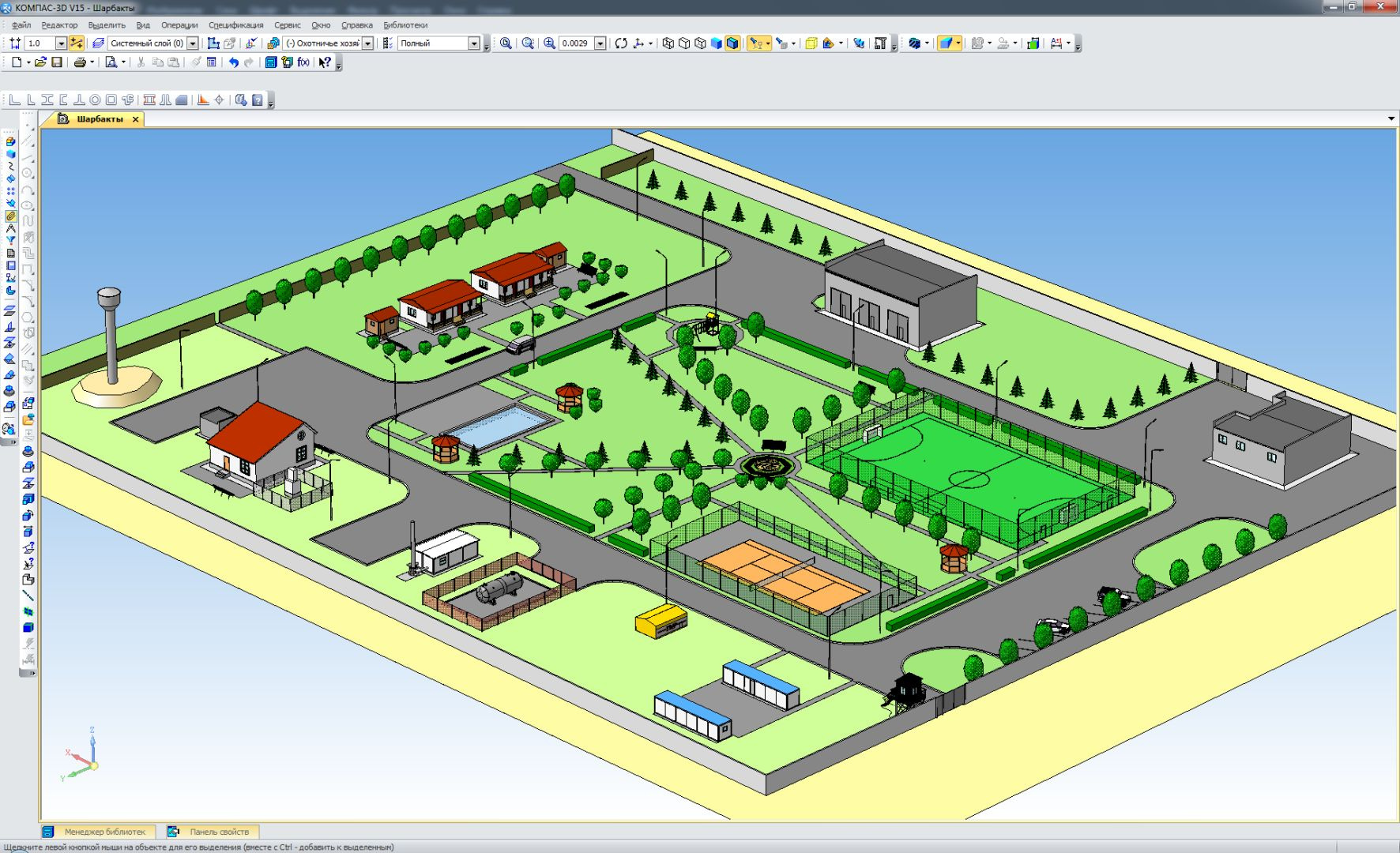
Охотничье хозяйство в натуральный размер. При увеличении модели все грани сохраняют форму (Картинка кликабельна)
Гладкость.
Сетка из треугольников для работы с чертежами не подходит - на чертеже нужны гладкие и чёткие контуры, а сетка создаст визуальную грязь.
Для примера рассмотрим куб. При проецировании его граничного представления на плоскость получится квадрат. В случае с полигональным представлением мы увидим квадрат с диагональю. Если же спроецировать в чертёж полигональный цилиндр, то диагоналей будет гораздо больше. Они и образуют визуальную грязь.
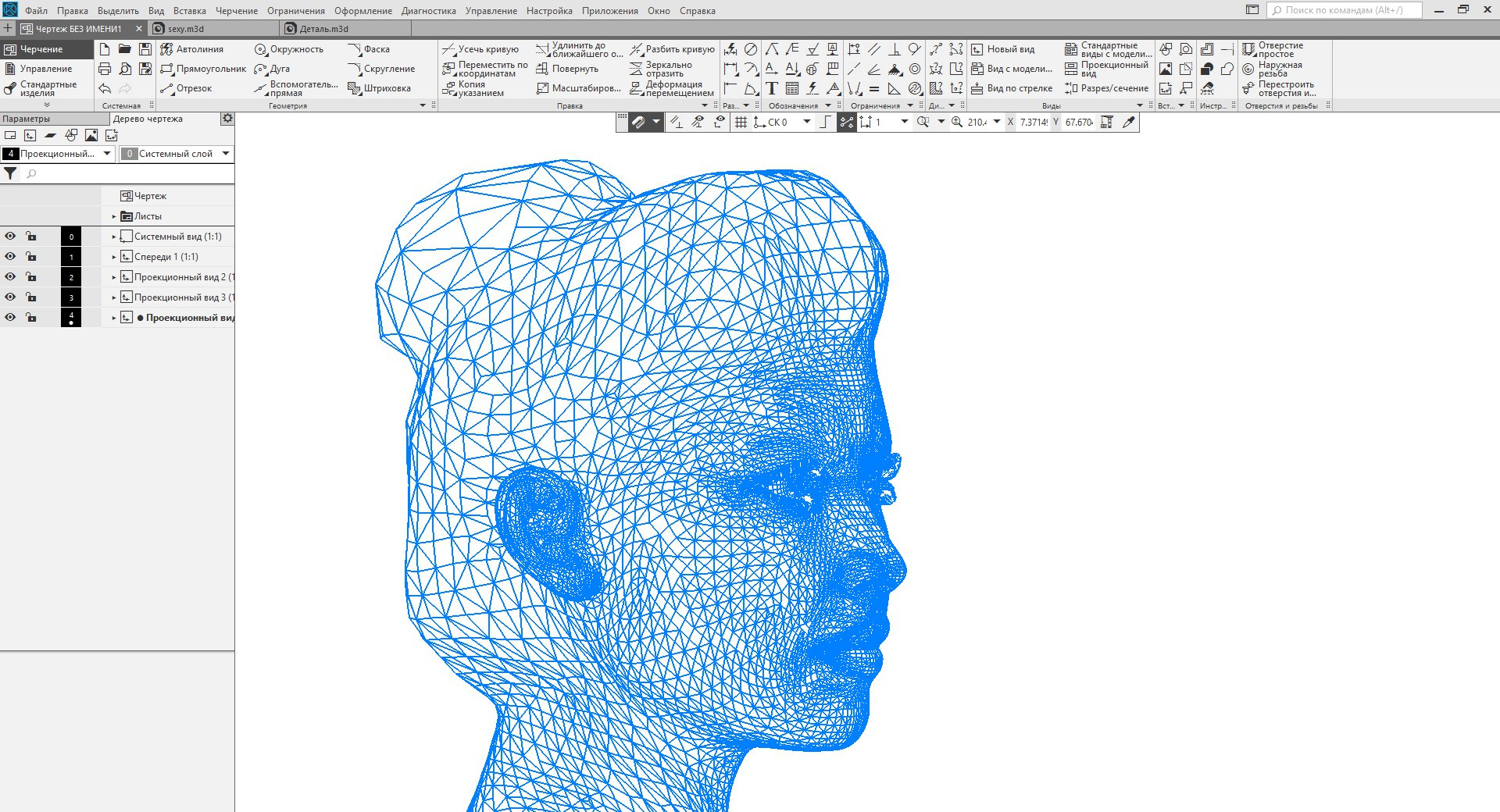
Пример передачи фасетной модели в чертёж. Видно как сливаются места сгущения сетки (Картинка кликабельна)
Точность.
Движение управляющих органов станка с числовым программным управлением, который работает с 3D-моделью, намного проще задавать с помощью математических формул.
Полигональное представление модели не позволяет построить точную траекторию режущего инструмента, так как исходная информация о форме изготавливаемого объекта отсутствует и заменена приближенной.
NB: Готовых CAM-форматов, которые бы принимали NURBS в качестве исходных данных, на сегодняшний день не существует. Встречаются отдельные энтузиасты, которые предлагают собственные версии G-кода, способного выполнять «NURBS interpolation», но пока это всё остаётся в области науки.
NB: Готовых CAM-форматов, которые бы принимали NURBS в качестве исходных данных, на сегодняшний день не существует. Встречаются отдельные энтузиасты, которые предлагают собственные версии G-кода, способного выполнять «NURBS interpolation», но пока это всё остаётся в области науки.

Обработка модели в CAM-системе Esprit
В действительности же причин значительно больше, но это – профессиональные тонкости.
Невероятно, но факт: современные системы проектирования (и КОМПАС-3D – не исключение) работают с двумя представлениями геометрии. Граничное представление используются в процессе моделирования, после чего производится расчёт триангуляционной сетки и строится полигональная модель, которая затем отправляется в видеокарту для отрисовки визуальной сцены. На данном этапе в процесс может вмешаться ядро визуализации, например C3D Vision, которое отвечает за управление отрисовкой модели с использованием средств математической, программной и аппаратной оптимизации. Подробнее об этом мы расскажем в следующих статьях.
Сложный выбор: купить ядро или написать собственное?
Каждый разработчик инженерного программного обеспечения рано или поздно оказывается перед выбором: писать ли необходимые математические алгоритмы самому или приобрести готовые компоненты на стороне? В истории АСКОН использование сторонних модулей рассматривалось в 1995 году, когда обсуждалась разработка КОМПАС-3D. Тогда был выбран тернистый пусть самостоятельного написания геометрических функций, в основе которых лежит довольно сложная математика. Подробнее ознакомиться с ней можно, прочитав книгу Николая Голованова по геометрическому моделированию:


Оглавление и обложка книги «Геометрическое моделирование» Н.Н. Голованова (Картинки кликабельны)
Мало кто знает, что позднее, в 2000-х годах, в АСКОН повторно рассматривался вопрос использования стороннего математического ядра для работы с 3D. Было произведено тестирование доступных на рынке CAD-компонентов и принято стратегически важное решение о продолжении разработки собственного геометрического ядра. Оно получило имя C3D, что является сокращением от внутрикорпоративного названия проекта «Core3D». Сегодня это ядро успешно используется не только внутри АСКОН, но и в проектах других разработчиков систем автоматизированного проектирования в России и за рубежом.
Вторая часть статьи

Аркадий Камнев
Менеджер по маркетингу в C3D Labs