Вот уже более полугода в компании используется единая система для проведения A/B-экспериментов. Одной из самых важных частей этой системы является процедура проверки качества, которая помогает нам понять, насколько мы можем доверять результатам A/B-тестов. В этой статье мы подробно опишем принцип работы процедуры проверки качества в расчете на тех читателей, которые захотят проверить свою систему A/B-тестирования. Поэтому в статье много технических деталей.
Несколько слов про A/B-тестирование
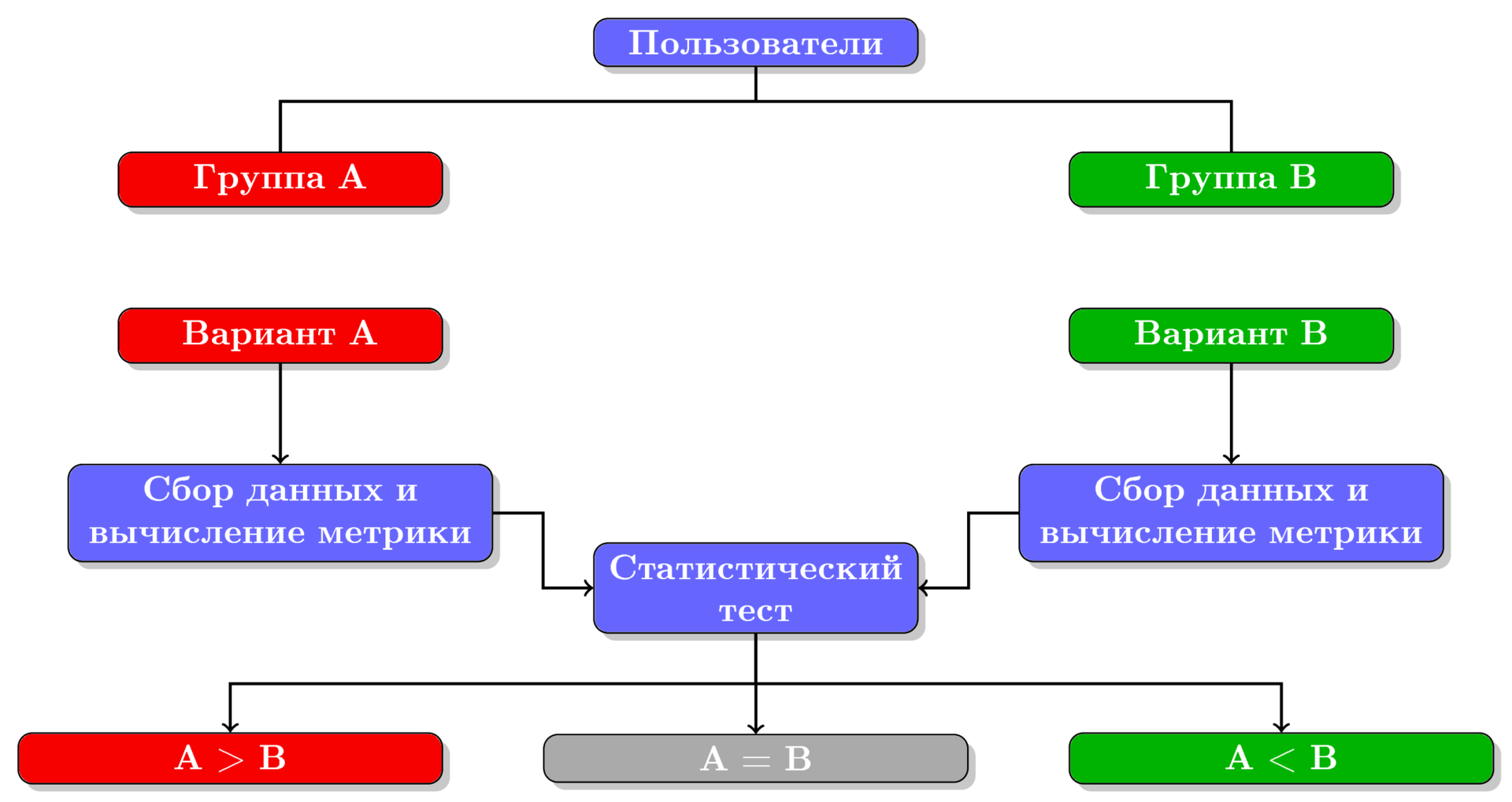
Рисунок 1. Схема процесса A/B-тестирования.
В целом процесс A/B-тестирования можно разделить на следующие шаги (показанные на рисунке):
- Распределение пользователей по двум группам A и B.
- Представление двум группам пользователей двух различных вариантов.
- Сбор данных и вычисление значения метрики для каждой группы.
- Сравнение с помощью статистического теста значений метрики в обеих группах и принятие решения, какой из двух вариантов выиграл.
В принципе, с помощью A/B-тестов можно сравнивать любые два варианта, но мы, для определенности, будем считать, что группе A показывается текущий вариант, работающий в продакшене, а группе B — экспериментальный вариант. Таким образом, группа A — контрольная группа, а группа B — экспериментальная. Если пользователям в группе B показывается такой же вариант, как и в группе A (то есть между вариантами A и B нет никакой разницы), то такой тест называют A/A-тестом.
Если в A/B-тесте победил один из вариантов, то говорят, что тест прокрасился.
История A/B-тестирования в компании
A/B-тестирование в компании HeadHunter началось, можно сказать, стихийно: команды разработчиков произвольно делили аудиторию на группы и проводили эксперименты. При этом общего пула проверенных метрик не было — каждая команда вычисляла свои собственные метрики из логов действий пользователей. Общей системы определения победителя тоже не было: если один вариант сильно превосходил другой, то он признавался победителем; если разница между двумя вариантами была небольшой, то для определения победителя применялись статистические методы. Хуже всего было то, что разные команды могли проводить эксперименты на одной и той же группе пользователей, тем самым влияя на результаты друг друга. Стало понятно, что нам нужна единая система для проведения A/B-тестов.
Такая система была создана и запущена в июле 2016 года. С помощью этой системы в компании уже проведено 77 экспериментов. Количество A/B-экспериментов по месяцам показано на рисунке 2.
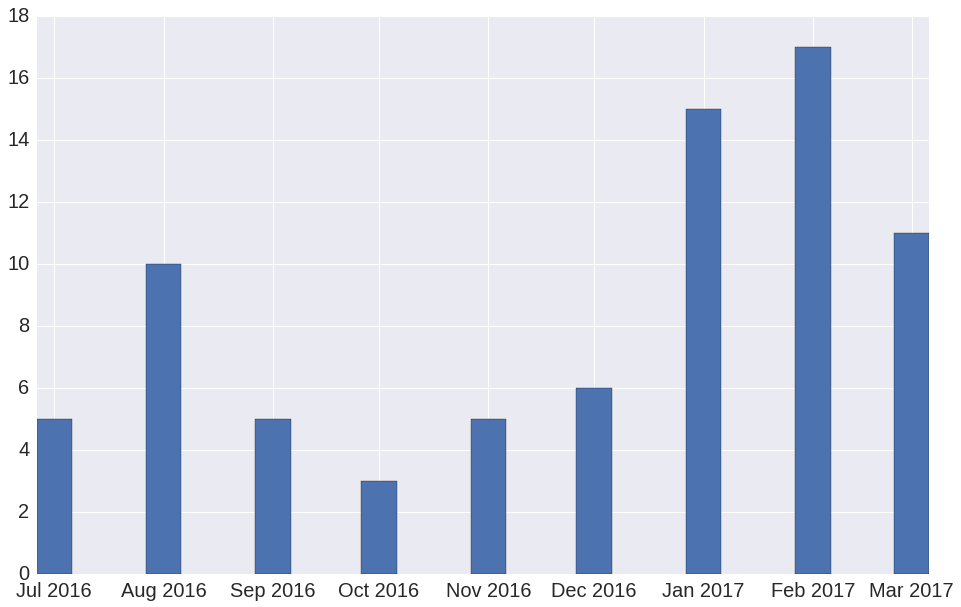
Рисунок 2. Число A/B-экспериментов по месяцам с момента запуска системы A/B-тестирования. Число экспериментов за март 2017 неполное, т.к. на момент публикаций этот месяц еще не закончился.
При создании системы A/B-тестирования мы уделили наибольшее внимание статистическому тесту. В первую очередь нас интересовал ответ на следующий вопрос:
Как убедиться в том, что статистический тест нас не обманывает и мы можем доверять его результатам?
Вопрос вовсе не праздный, поскольку вред от некорректных результатов стат. теста может быть даже больше, чем от отсутствия результатов.
Почему у нас могут быть причины не доверять стат. тесту? Дело в том, что статистический тест предполагает вероятностную интерпретацию измеряемых величин. Например, мы считаем, что у каждого пользователя есть «вероятность» совершить некое успешное действие (успешными действиями могут быть регистрация, покупка товара, лайк и т. д.). При этом мы считаем действия разных пользователей независимыми. Но изначально мы не знаем, насколько хорошо действия пользователей соответствуют вероятностной модели стат. теста.
Чтобы оценить качество системы A/B-тестирования, мы проводили большое количество A/A-тестов и измеряли процент прокрасившихся тестов, то есть процент случаев, в которых стат. тест ошибался, утверждая о статистически значимом превосходстве одного варианта над другим. О пользе A/A-тестов можно прочитать, например, здесь. Измеренный процент ошибок стат. теста сравнивался с заданным теоретическим значением: если они примерно совпадали, значит, все хорошо; если измеренный процент ошибок сильно меньше или сильно больше теоретического, значит, результаты такого стат. теста ненадежны.
Чтобы рассказать подробнее о методе оценки качества системы A/B-тестирования, следует сначала рассказать про уровень значимости и про другие понятия, возникающие при проверке статистических гипотез. Читатели, знакомые с данной темой, могут пропустить следующий параграф и перейти к параграфу Оценка качества системы A/B-тестирования.
Статистический тест, доверительные интервалы и уровень значимости
Давайте для начала рассмотрим простой пример. Пусть у нас всего 6 пользователей и мы разбили их на 2 группы по 3 человека, провели A/B-тест, подсчитали значение метрики для каждого отдельного пользователя и получили в результате такие таблицы:
| Пользователь |
Значение метрики |
|---|---|
| А. Антонов | 1 |
| П. Петров | 0 |
| С. Сергеев | 0 |
| Пользователь |
Значение метрики |
|---|---|
| Б. Быстров | 0 |
| В. Вольнов | 1 |
| У. Умнов | 1 |
Среднее значение метрики в группе A равно
То есть, кроме разности средних значений метрики в двух группах, нам еще хотелось бы оценить и доверительный интервал для истинного значения разности
Представить себе, что означает уровень значимости, можно так. Если мы много раз будем повторять A/A-тест, то процент случаев, в которых A/A-тест прокрасится, будет примерно равен
Собственно, статистический тест как раз и занимается оценкой доверительного интервала для разности
- Если обе границы доверительного интервала больше 0, значит, выиграл вариант B.
- Если 0 внутри интервала, значит, ничья — ни один из вариантов не выиграл.
- Если обе границы меньше 0, значит, выиграл вариант A.
Например, предположим, что мы как-то смогли узнать, что для уровня значимости
Нам осталось понять, как статистический тест из уровня значимости и экспериментальных данных оценивает доверительные интервалы для разности значений метрики между группами A и B.
Определение доверительных интервалов
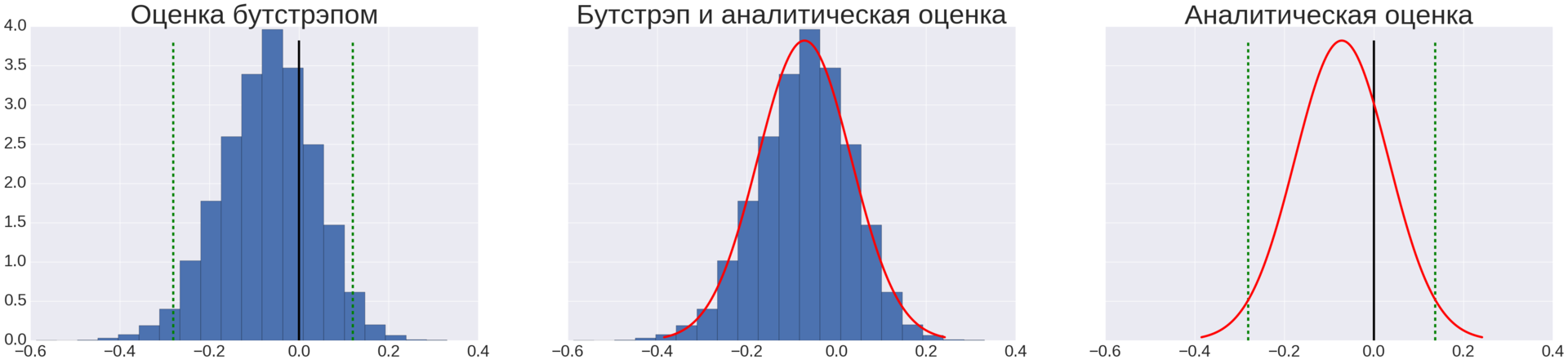
Рисунок 3. Оценка доверительных интервалов для разности
Для определения доверительных интервалов мы пользовались двумя способами, показанными на рисунке 3:
- Аналитически.
- С помощью бутстрэпа.
Аналитическая оценка доверительных интервалов
В аналитическом подходе мы опираемся на утверждение центральной предельной теоремы (ЦПТ) и ожидаем, что разность средних значений метрик в двух группах будет иметь нормальное распределение, с параметрами
Где средние значения (
по стандартным формулам.
Зная параметры нормального распределения и уровень значимости, мы можем вычислить доверительные интервалы. Формулы для вычисления доверительных интервалов мы не приводим, но идея показана на рисунке 3 на правом графике.
Одним из минусов такого подхода является тот факт, что в ЦПТ случайные величины предполагаются независимыми. В реальности это предположение часто нарушается, в частности, из-за того, что действия одного пользователя зависимы. Например, пользователь «Амазона», купивший одну книгу, скорее всего, купит и еще одну. Будет ошибкой считать две покупки одного пользователя независимыми случайными величинами, потому что мы можем в результате получить слишком оптимистичную оценку на доверительный интервал. А это означает, что в реальности процент ложно прокрасившихся A/A-тестов может быть в разы больше, чем заданное значение. Именно это мы и наблюдали на практике. Поэтому мы попробовали другой метод оценки доверительных интервалов, а именно бутстрэп.
Оценка доверительных интервалов с помощью бутстрэпа
Бутстрэп — это один из методов непараметрической оценки доверительных интервалов, в котором не делается никаких предположений о независимости случайных величин. Применение бутстрэпа для оценки доверительных интервалов сводится к следующей процедуре:
- Повторять
раз:
- выбрать с помощью бутстрэпа случайные подвыборки значений из групп A и B;
- подсчитать разность средних значений
в этих подвыборках;
- Упорядочить по возрастанию значения, полученные на каждой итерации
- С помощью упорядоченного массива
определить доверительный интервал так, чтобы
точек лежали внутри интервала. То есть, левой границей интервала будет число с индексом
, а правой границей — число с индексом
в упорядоченном массиве.
На рисунке 3 на левом графике показаны гистограмма для массива значений разности, полученного после 10 000 итераций бутстрэпа, и доверительные интервалы, вычисленные по описанной здесь процедуре.
Оценка качества системы A/B-тестирования
Итак, мы разбили всех пользователей на
Вычислить
- Если
, то либо стат. тест, либо выбранная метрика слишком консервативны. То есть у A/B-тестов заниженная чувствительность («стойкий оловянный солдатик»). И это плохо, т. к. в процессе эксплуатации такой системы A/B-тестирования мы будем часто отклонять изменения, которые действительно что-то улучшили, т. к. мы не почувствовали улучшения (т. е. мы будем часто совершать ошибку второго рода).
- Если
, то либо стат. тест, либо выбранная метрика слишком чувствительны («принцесса на горошине»). Это тоже плохо, т. к. в процессе эксплуатации мы будем часто принимать изменения, которые в действительности ни на что не влияли (т. е. мы будем часто совершать ошибку первого рода).
- Наконец, если
, значит, стат. тест вместе с выбранной метрикой показывают хорошее качество и такой системой можно пользоваться для проведения A/B-тестирования.
 |
 |
| (а) Перебираем все возможные пары | (б) Случайно разбиваем на непересекающиеся пары |
| Рисунок 4. Два варианта разбиения 4 групп пользователей ( |
|
Итак, нам нужно провести много A/A-тестов, чтобы лучше оценить процент ошибок стат. теста
Однако такой подход обладает серьезным недостатком, а именно: мы получаем большое число зависимых пар. Например, если в одной группе среднее значение метрики очень мало, то большинство A/A-тестов для пар, содержащих эту группу, прокрасится. Поэтому мы остановились на подходе, показанном на рисунке 4 (б), в котором все группы разбиваются на непересекающиеся пары. То есть число пар равно
Результаты применения A/A-теста к 64 группам пользователей, которые разбились на 32 независимые пары, показаны на рисунке 5. Из этого рисунка видно, что из 32 пар прокрасились только 2, то есть

Рисунок 5. Результаты A/A-тестов для 64 групп пользователей, случайно разбитых на 32 пары. Доверительные интервалы вычислялись с помощью бутстрэпа, уровень значимости — 5%.
Гистограммы значений
В принципе, на этом можно было бы и остановиться. У нас есть способ вычислить реальный процент ошибок стат. теста. Но в этом способе нас смущало небольшое число A/A-тестов. Кажется, что 32 A/A-теста — это маловато для надежного измерения величины
Если число пар невелико, то как нам надежно измерить
Мы использовали такое решение: давайте много раз случайно перераспределять пользователей по группам. И после каждого перераспределения мы сможем измерять процент ошибок
В итоге мы получили следующую процедуру для оценки качества системы A/B-тестирования:
- Повторять
раз:
- Случайно распределить всех пользователей по
группам;
- Случайно разбить
групп на
пар;
- Для всех пар провести A/A-тест и вычислить процент прокрасившися пар
на данной
-ой итерации
- Случайно распределить всех пользователей по
- вычислить
как среднее по всем итерациям:
Если в процедуре оценки качества системы A/B-тестирования мы зафиксируем стат. тест (например, всегда будем использовать бутстрэп) и поверим, что сам стат. тест непогрешим (или незаменим), то у нас получится система оценки качества метрик.
Пример оценки качества одной из метрик показан на рисунке 6. Из этого графика видно, что средний процент ошибок стат. теста (т.е. значение

Рисунок 6. Результат оценки качества для метрики успешных действий пользователей. Синим показана гистограмма для массива чисел
Результаты оценки качества метрик
 |
 |
 |
| (a) |
(б) |
(в) |
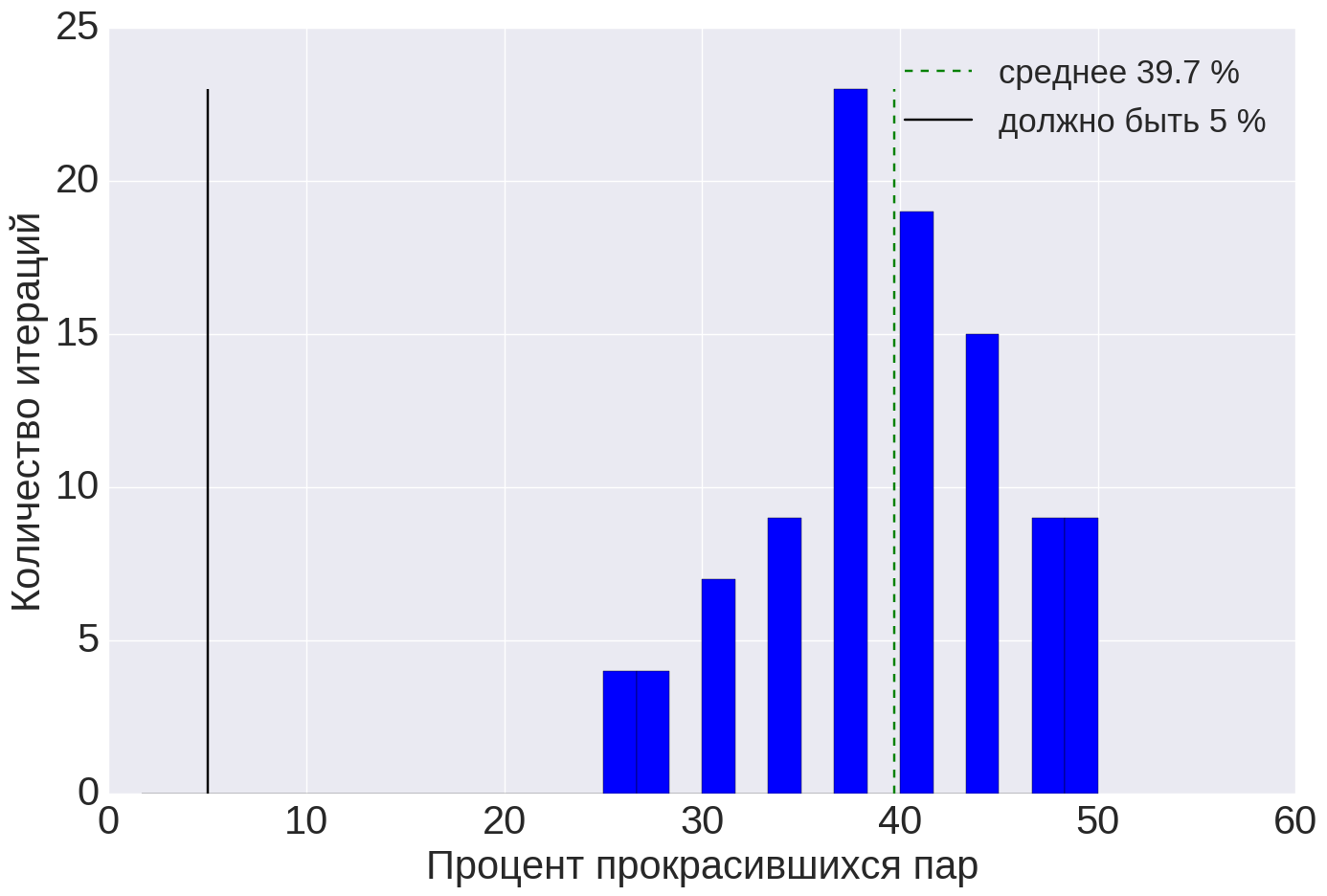
| Рисунок 7. Результаты оценки качества для метрики успешности поисковых сессий: (а) — для исходной метрики и бутстрэпа по значениям, (б) — для исходной метрики и бутстрэпа по пользователям, (в) — для модифицированной метрики и бутстрэпа по значениям. |
||
Когда мы применили процедуру оценки качества к метрике успешности поисковых сессий, то получили такой результат, как на рисунке 7 (а). Стат. тест в теории должен ошибаться в 5% случаев, а в реальности ошибается в 40% случаев! То есть, если мы будем использовать данную метрику, то 40% A/B-тестов будут прокрашиваться, даже если вариант А ничем не отличается от варианта Б.
Данная метрика оказалась «принцессой на горошине». Однако мы все же хотели использовать эту метрику, так как ее значение имеет простую интерпретацию. Поэтому мы стали разбираться, в чем может быть проблема и как с этим можно справиться.
Мы предположили, что проблема может быть связана с тем, что от одного пользователя в метрику попадает несколько значений, которые зависимы. Пример ситуации, когда от одного пользователя (Иван Иванович) в метрику попадает два числа, показан в таблице 3.
| Пользователь |
Значение метрики |
|---|---|
| Иван Иванович | 0 |
| Иван Никифорович | 0 |
| Антон Прокофьевич | 1 |
| Иван Иванович | 1 |
Ослабить влияние зависимости значений одного пользователя мы можем либо модификацией стат. теста, либо изменением метрики. Мы попробовали оба этих варианта.
Модификация стат. теста
Поскольку значения от одного пользователя зависимы, то мы выполняли бутстрэп не по значениям, а по пользователям: если пользователь попал в бутстрэпную выборку, то используются все его значения; если не попал, то не используется ни одно из его значений. Применение такой схемы привело к значительному улучшению (рисунок 7 (б)) — реальный процент ошибок стат. теста на 100 итерациях оказался равным
Модификация метрики
Если нам мешает, что от одного пользователя в метрику попадает несколько зависимых значений, то можно сначала усреднить все значения внутри пользователя, чтобы от каждого пользователя в метрику попадало бы только одно число. Например, таблица 3 после усреднения значений внутри каждого пользователя перейдет в следующую таблицу:
| Пользователь |
Значение метрики |
|---|---|
| Иван Иванович | 0.5 |
| Иван Никифорович | 0 |
| Антон Прокофьевич | 1 |
Результаты оценки качества метрики после данной модификации показаны на рисунке 7 (в). Процент случаев, в которых стат. тест ошибался, оказался почти в 2 раза ниже теоретического значения
Какой из двух подходов лучше
Мы применяли оба подхода (модификация стат. теста и модификация метрики) для оценки качества различных метрик, и для подавляющего большинства метрик оба подхода показывали хорошие результаты. Поэтому использовать можно тот способ, который проще реализовать.
Выводы
Главный вывод, который мы сделали при оценке качества системы A/B-тестирования: нужно обязательно выполнять оценку качества системы A/B-тестирования). Перед тем как использовать новую метрику, ее нужно проверить. Иначе A/B-тесты рискуют превратиться в одну из форм гадания и повредить процессу разработки.
В этой статье мы постарались, насколько это возможно, привести всю информацию о устройстве и принципах работы процедуры оценки качества системы A/B-тестирования, используемой в компании. Но если у Вас остались вопросы, не стесняйтесь задавать их в комментариях.
P.S.
Я хотел бы выразить благодарность lleo за систематизацию процесса A/B-тестирования в компании и за проведение proof-of-concept экспериментов, развитием которых является данная работа, и p0b0rchy за передачу опыта, терпеливые многочасовые разъяснения и за генерацию идей, которые легли в основу наших экспериментов.
