В преддверии первого квалификационного раунда Russian Code Cup, который состоится 19 апреля, мы решили рассказать вам о семи самых интересных задач RCC за всю историю чемпионата по мнению Андрея Станкевича — доцента кафедры компьютерных технологий ИТМО, лауреата Премии Президента Российской Федерации в области образования, лауреата премии ACM-ICPC Founder’s Award, лауреата специальной премии корпорации IBM за успехи в тренерской работе.
Напоминаем, для того чтобы принять участие в Russian Code Cup, нужно зарегистрироваться на сайте http://russiancodecup.ru/ (регистрация будет открыта до начала третьего квалификационного раунда).

2011 год, Финальный раунд, «B» Обратная задача о черепашке
2011 год, Финальный раунд, «D» Архиватор
2012 год, 2-й квалификационный раунд, «C» Тетраэдр
2012 год, Отборочный раунд, «F» Принц
2012 год, Финальный раунд, «E» Перемешивание колоды
2013 год, Отборочный раунд, «E» Лазеры
2013 год, Финальный раунд, «D» Робот
1) 2011 год, Финальный раунд, «B» Обратная задача о черепашке
Разбор:
В этой задаче требовалось по заданному числу k построить лабиринт, в котором количество путей из левой верхней в нижнюю правую клетку было бы равно k при условии, что разрешается двигаться только вправо и вниз.
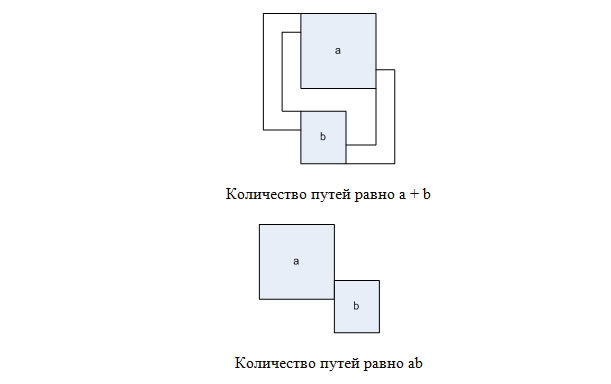
Заметим следующее. Пусть у нас есть два лабиринта, в которых количество способов добраться от верхней левой до правой нижней клетки равно a и b соответственно.
Тогда, разместив их параллельно, как показано на рисунке, мы можем получить лабиринт, для которого есть a + b способов добраться из верхней левой до нижней правой клетки. А разместив их последовательно — получить лабиринт, в котором ab путей.
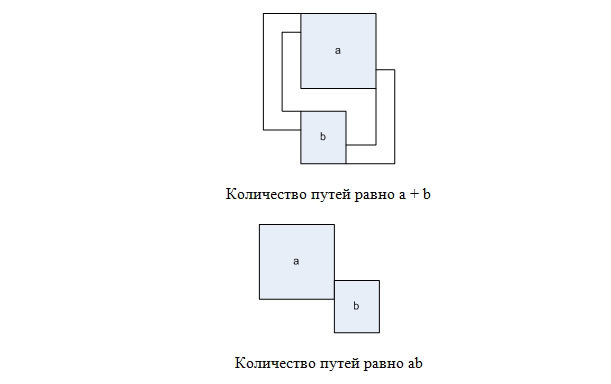
Заметим, что в пустом лабиринте размером 2×2 существует два пути, а в лабиринте размера 1×1 — один путь. Следовательно, разложив число k в двоичную систему счисления и используя описанный метод, можно получить лабиринт с k путями из верхней левой в правую нижнюю клетку.
Пример такого лабиринта для k = 19 приведен на рисунке.
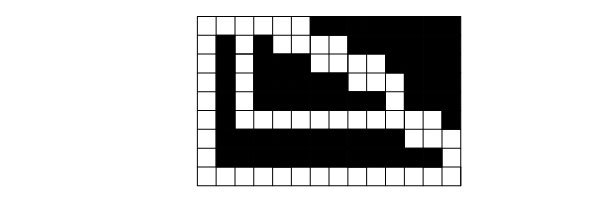
Заметим, что на каждый разряд числа k требуется 5 клеток по горизонтали, а 260 > 1018, поэтому приведенная схема позволяет создать лабиринт размером не более 300×300, что и требуется в условии задачи.
2) 2011 год, Финальный раунд, «D» Архиватор
Разбор:
К этой задаче возможно как минимум два различных подхода: динамическое программирование или жадный алгоритм.
Представим процесс архивации последовательности в виде дерева: каждый символ каждой из промежуточных последовательностей будет вершиной дерева, детьми вершины будут два символа, которые «склеиваются» в процессе архивации в заданный. В листьях записаны исходные числа, а задача состоит в том, чтобы во все промежуточные вершины записать числа, при этом штраф за архивацию равен числу вершин, у которых в детях записаны различные числа.
Решение с помощью динамического программирования устроено следующим образом: в каждой вершине u будем хранить минимальный суммарный штраф p[u][x] для поддерева, если в этой вершине записать число x. Заметим, что в вершине осмысленно записывать только число, которое встречается в одном из листьев в поддереве, поэтому суммарное количество вариантов, которое следует рассмотреть, есть O(n log n).
Пересчет осуществляется следующим образом: рассмотрим вершину u с детьми v и w. Пусть мы планируем записать значение x. Если оба значения p[v][x] и p[w][x] определены, то один из вариантов поставить x в u — это поставить x в обоих детей, цена этого варианта p[v][x] + p[w][x]. Также есть вариант поставить x лишь в одного ребенка. Пусть мы планируем поставить x в v, тогда стоимость этого варианта p[v][x] + minp[w] + 1, где minp[w] — минимальное значение p[w][y] по всем y.
Альтернативой решению с помощью ДП является жадное решение: для каждой вершины будем хранить список всех возможных значений, поставив одно из которых в вершину мы получим минимальный штраф в поддереве. Оказывается, что для того, чтобы найти оптимальное множество для вершины, достаточно пробовать поставить в ее детей лишь оптимальные значения. При этом, если списки оптимальных значений для детей пересекаются, то необходимо взять одно из таких чисел. Если же они не пересекаются, то подойдет любое из значений каждого из детей.
Доказательство корректности приведенного алгоритма оставим в качестве упражнения.
3) 2012 год, 2-й квалификационный раунд, «C» Тетраэдр
Разбор:
Напомню, что тетраэдр — это многогранник, гранями которого являются четыре треугольника (другими словами — треугольная пирамида).
Все начинается с того, что мы перебираем возможные соответствия спичек ребрам тетраэдра. Обозначим искомый тетраэдр как ABCD. У него шесть ребер: AB, AC, AD, BC, BD и CD. Переберем все 6! = 720 вариантов, какая спичка соответствует какому ребру. Теперь осталось проверить, что соответствующий тетраэдр существует.
Как проверить существование тетраэдра? Здесь есть как минимум три решения.
Первое решение основывается на вычислении объема тетраэдра. Самое простое решение — найти формулу для расчета объема тетраэдра по граням. Эта задача сама по себе непростая, приведу здесь формулу:
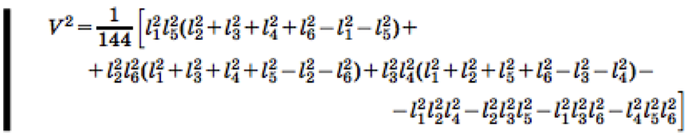
Соответственно, если правая часть равенства оказывается отрицательной или треугольники в гранях построить нельзя (неравенство треугольника), то тетраэдр не сойдется.
Для интересующихся — здесь эта формула выводится.
Второй подход к решению задачи — геометрический. Сначала убедимся, что ABC и BCD существуют. Теперь попытаемся сделать тетраэдр. Понятно, что при построении объемной фигуры проблема может возникнуть только с последним ребром — оно может оказаться или слишком длинным, или слишком коротким. Поэтому в этом решении предлагается найти диапазон длины последнего ребра.
Есть два предельных варианта размещения граней, при которых тетраэдр превращается в плоскую фигуру. Первый — когда грани развернуты друг относительно друга на 180 градусов (CAB и CBD), и вторая — когда они «сложены» и образуют «нулевой угол» (CA’D и CDB). Все допустимые положения граней друг относительно друга находятся в диапазоне между этими граничными. Наибольшей своей длины последнее ребро (A-D) достигает в первом предельном варианте (AD), а наименьшей — в последнем (A’D). Следовательно, тетраэдр будет существовать, если эта длина последнего ребра укладывается в найденный нами диапазон (от A’D до AD).
Для того, чтобы найти расстояние между точками A и D и A’ и D, найдем сначала их координаты, приняв за ноль одну из общих для треугольников вершин, а ось абсцисс проведем через одно из ребер, исходящих из этой вершины. Найти координаты всех остальных вершин в этой системе координат довольно просто: через соотношения сторон и косинусы углов мы определим положения вершин в полярных координатах (угол, расстояние), после чего переведем их в декартову систему координат. Зная координаты вершин, вычислить максимальное и минимальное расстояния между несвязанными вершинами совсем просто.
Программа должна проверять, умещается ли длина оставшейся грани в указанные диапазоны. Если да, то тетраэдр из таких длин «собрать» можно.
Третий способ также геометрический. Сначала необходимо проверить существование всех треугольников с указанными сторонами. Если хотя бы один треугольник не может быть построен по указанным значениям сторон, то тетраэдр также не может быть построен. Для проверки необходимо проверить неравенство невырожденного треугольника: любая из его сторон должна быть строго меньше суммы двух других.
Во многих случаях решение этим и ограничилось; между тем существуют ситуации, когда треугольники с указанными сторонами могут быть построены, а тетраэдр из них собрать невозможно.
Например, если мы имеем грани (100,100,2,101,100,2), то треугольники (100,100,2) и (101,100,2) формально удовлетворяют неравенству треугольника, но тетраэдр сложить из таких треугольников невозможно. Из рисунка мы видим, что ребро AC почти параллельно AB, значит, расстояние от D до C почти не будет меняться при любом наклоне грани ABD относительно AB, из чего можно заключить, что DB почти перпендикулярно BC. В этом случае DC можно приблизительно оценить как корень из суммы квадратов катетов, то есть DC должно быть приблизительно около 10, а совсем не 2, как мы предположили в условии.
Следовательно, кроме проверки на треугольники в гранях, необходимо выполнить дополнительную проверку на трехгранные углы. Необходимых и достаточных условий существования трехгранного угла два:
Плоский угол находится через теорему косинусов для треугольника.
Всего было направлено на проверку 1088 решений, из них правильных всего 74 (7%). 8% участников Russian Code Cup QR2 справились с этой задачей. Первое решение пришло от участника с ником AVictor через 30 минут после начала раунда.
4) 2012 год, Отборочный раунд, «F» Принц
Разбор:
В этой задаче необходимо найти минимальное время, за которое принц попадет к принцессе по одномерному коридору, не попав ни в одну ловушку. Известны расписание, размеры и места появления/исчезновения ловушек, а также скорость движения принца. Поскольку коридор одномерный, то двигаться принц может либо по направлению к принцессе, либо от нее, либо никуда не двигаться вообще. Очевидно, существуют ситуации, когда выхода нет, и принц не попадет к принцессе — в этом случае нужно вывести Impossible.
Решение этой задачи стоит начать с того, что изобразить ловушки на плоскости, где координатой x является позиция в коридоре, а координатой y — время. Теперь задачу можно переформулировать в понятиях этой плоскости: требуется попасть из точки (0, 0) в точку (x, y) с минимальным y, при этом разрешено двигаться вертикально вверх (стоять на месте), по диагонали направо вверх и налево вверх (двигаться по коридору) и запрещено заходить в определенные прямоугольники (ловушки). Находиться на границе прямоугольника разрешено.
Оптимальный путь в такой задаче будет состоять из множества однотипных частей, каждая из которых будет состоять из движения по одной из диагоналей до координаты, соответствующей границе одного из прямоугольников, с последующим движением вертикально вверх до верхнего угла этого прямоугольника. Таким образом, ключевыми точками являются верхние левые и верхние правые углы каждого прямоугольника и про них необходимо выяснить, можно ли туда попасть.
При движении по диагонали будем поддерживать множество прямоугольников, находящихся над текущей позицией. Так как на границе прямоугольников находиться можно, то прямоугольники, начинающиеся или заканчивающиеся на текущей «коридорной» координате, учитывать не будем. Прямоугольники будем хранить в множестве, упорядоченными по нижнему краю. Такое множество будем называть срезом. Для хранения множества можно использовать структуры данных, подобные красно-черным или декартовым деревьям или очереди с приоритетом. Нижний край нижнего прямоугольника будем называть краем среза. Если срез не содержит прямоугольников, то будем считать его край бесконечностью.
Так как при любом движении увеличивается координата времени, то будем рассматривать углы прямоугольников в порядке неубывания этой координаты. Рассматривая очередной угол, попытаемся двигаться от него по диагонали в обе стороны. Движение осуществляется по координатам, соответствующим границам прямоугольников. Достигая очередной координаты, проверяем, можно ли, двигаясь вертикально вверх, попасть в соответствующий верхний угол какого-либо прямоугольника. Достичь угла можно, если этот угол находится не выше края текущего среза. Также необходимо проверить, что движение не уперлось в край одного из прямоугольников, начинающихся в данной координате. Если удалось достигнуть координаты двери x, то необходимо обновить текущий ответ. Если при движении от одной координаты к другой был превышен край среза, то при переходе был достигнут нижний край прямоугольника, и движение необходимо прекратить.
Поочередно рассмотрев все углы и шагая в обе стороны от каждого из них, найдем минимальный возможный ответ или информацию о том, что дверь не достижима. Описанный алгоритм совершает O(n2 log n) операций, так как необходимо из каждого из O(n) углов пройти по диагонали O(n) различных координат и проверить O(n) прямоугольников. Также для каждого угла приходится совершать O(n log n) операций для поддержания среза, так как необходимо добавлять и удалять из среза O(n) прямоугольников.
Далее приведены возможные варианты прохождения мимо прямоугольников, которые необходимо не забыть обработать.
и
В то же время на следующем тесте невозможно успеть попасть к двери.
Эта задача тоже не из простых — ее решили всего 23 человека, первым — Куликов Егор на 100:18. Тут стоит отметить Епифанова Владислава, отправившего решение этой задачи, последней для него, за 2 минуты до конца тура. Владислав занял первое место как в квалификации, так и на отборочном туре.
5) 2012 год, Финальный раунд, «E» Перемешивание колоды
Разбор:
О задаче про перемешивание колоды рассказывает Сергей МЕЛЬНИКОВ, студент НИУ ИТМО.
В этой задаче нужно продумать механизм перемешивания колоды, позволяющий за минимальное число перемещений блоков карт из середины в конец колоды идеально ее перемешать (то есть сделать так, чтобы никакие две одинаковые карты не шли друг за другом), либо сообщить, что идеально перемешать колоду невозможно. Изначально колода отсортирована по неубыванию достоинства. Дано количество разных достоинств карт, порядок карт в колоде, количество колод.
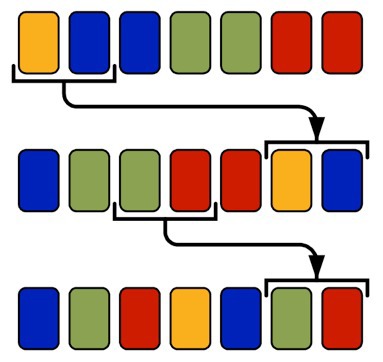
Подробная постановка задачи
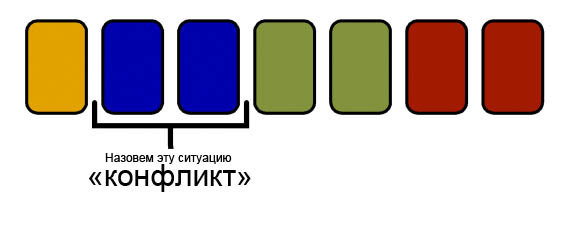
Назовем конфликтом ситуацию, в которой две одинаковые карты стоят подряд:
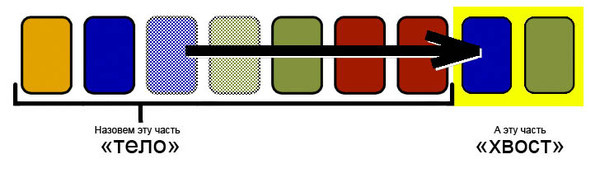
Назовем телом исходную последовательность карт, которую постепенно будем уменьшать, перенося карты в хвост. Хвост будет формироваться таким образом, чтобы карты в нем не образовывали конфликтов.
Преобразуем исходную последовательность в последовательность конфликтов и будем работать с новой последовательностью. Будем называть цветом конфликта число, написанное на карточках, его образующих. Каждый раз перенося отрезок карт в конец колоды, будем выбирать его концы внутри конфликтов.
Обозначим число конфликтов через K. Поскольку одна операция перемещения убирает не более двух конфликтов, задачу невозможно решить быстрее чем за ⌈K / 2⌉ операций (здесь и далее в описании встречаются конструкции ⌊…⌋ и ⌈…⌉ — это округление вниз и вверх соответственно).
Обозначим как M максимальное число конфликтов одного цвета и будем называть сами эти конфликты «максимальными». Научимся решать задачу в случае, когда M = ⌈K / 2⌉.
Также напомню, что по условиям задачи колода отсортирована по неубыванию достоинства.
К примеру, в колоде 1122333344 число М будет равно 3 (три конфликта 33), общее число конфликтов – 6. В данном случае M = ⌈K / 2⌉.
В рассматриваемом случае (не примере) есть два варианта:
Решения для этих случаев оптимальны, так как достигается нижняя граница числа операций ⌈K / 2⌉. Итого, мы умеем оптимально решать задачу, когда число «максимальных» конфликтов составляет половину всех конфликтов (с округлением вверх). Будем называть такой случай базовым.
Теперь классифицируем исходные ситуации по максимальному числу карточек одного достоинства подряд. Будем называть эти карточки максимальными и обозначим их количество как Q.
Теперь будем каждый раз удалять последнюю пару конфликтов, которую можно удалить (два последних конфликта разного цвета) (C1, C2). Если в процессе попадем в базовый случай, то будем решать так, как решаем его. Если больше конфликтов не осталось, то задача решена.
Докажем, что новых конфликтов не возникнет. Рассмотрим цвет последнего конфликта Z, мы будем переносить пары конфликтов (X, Z) пока Z не кончится, при этом на конце останется Z, и получим хвост Z (X1, Z) (X2, Z)…. Если Z-конфликты кончатся, то будет переход на (X, Y) конфликты, то есть пара (Xk, Z) (Xk+1, Y), при Xk+1 ≠ Z.
При переходе к базовому случаю конфликтов не возникнет, потому что после переноса пары (X, Z) ни X, ни Z не могут стать максимальными (M). Так как M ≠ Z, то либо Z кончились и конфликта (X, Z) (Z, ...) не возникнет, либо Z находится после M, то есть получим продолжение (X, Z) (M, Z).
Так как мы на каждом шаге удаляем пару конфликтов, либо используем базовый случай, то построенное решение оптимально и работает за ⌈K / 2⌉ операций.
Можно заметить, что нет необходимости хранить информацию о том, какие числа и в каком порядке записаны в хвосте, поскольку там нет конфликтов. Последовательность значений можно поддерживать при помощи декартового дерева по неявному ключу, при этом суммарное время работы составит O(N log N). Также, если в какой-то момент мы определяем, что в конце тела нет конфликтов, то можно уменьшить длину тела и, соответственно, увеличить хвост. Можно рассмотреть все случаи, когда происходит перемещение отрезка, и убедиться, что тело всегда будет иметь вид: префикс исходного массива с не более чем двумя вырезанными подотрезками. Основываясь на этом факте, можно реализовать решение за O(n), но для решения данной задачи в данных ограничениях этого не требуется.
Задачу «Перемешивание карт» решил только Евгений КАПУН
6) 2013 год, Отборочный раунд, «E» Лазеры
Разбор:
Основная идея решения — двоичный поиск по ответу. Зафиксируем максимальный угол отклонения α и проверим существование решения с таким ответом. Для этого сведем задачу к поиску пути в графе.
Обозначим точки, заданные в условии, как P1, P2, ..., Pn. Построим граф из n(n — 1) вершин, где каждая вершина — это упорядоченная пара различных точек. Проведем ребра из пары (i, j) в пару (j, k) в том случае, если угол между векторами PiPj и PjPk не превосходит α. В построенном графе не более чем n3 ребер. Теперь, если в таком графе существует путь из вершины вида (1, i) в вершину вида (j, 1), то при таком α эксперимент осуществить можно. Проверять существование пути можно с помощью любого алгоритма поиска пути в графе.
Таким образом, одна итерация двоичного поиска работает за O(n3), а значит, весь алгоритм можно реализовать за O(n3 log(1/ε)) или, если заметить, что пространство поиска на самом деле дискретно (нас интересуют лишь не более чем n3 углов), то этот алгоритм можно реализовать за O(n3 log(n3)).
7) 2013 год, Финальный раунд, «D» Робот
Разбор:
В данной задаче необходимо было найти матожидание длины кратчайшего пути из одного угла поля в другой. При этом некоторые клетки поля были покрашены в белый цвет, и при попадании робота на такую клетку он переставлялся в случайную белую клетку поля.
Разберемся подробнее, как устроена оптимальная стратегия выбора пути. Для каждой клетки поля можно посчитать матожидание количества ходов, необходимых для того, чтобы попасть в правую нижнюю клетку. При этом ответ будет соответствовать расстоянию, которое записано в левой верхней клетке. Как же вычислить эти значения? Рассмотрим конкретную клетку и все соседние с ней. Если соседняя клетка покрашена в черный цвет, то ответ для клетки будет как минимум (1 + значение, которое записано в соседней клетке). Если же у клетки есть белый сосед, то ответ для нее равен как минимум (1 + среднее арифметическое ответов для всех белых клеток).
Понятно, что если робот два раза попадает в одну и ту же клетку, то существует оптимальная стратегия, в которой следующий ход в обоих случаях одинаковый. Если это не так, то на каком-то из ходов робот поступил неправильно и пошел в клетку с большим матожиданием количества ходов до конца, а значит, стратегию можно улучшить. Есть два принципиально разных действия, которые может сделать робот, находясь в некоторой клетке. Он может пойти сразу в правый нижний угол по черным клеткам (если такой путь существует), а может пойти в некоторую белую клетку. Очевидно, что среди всех белых клеток, в которые можно пойти, следует выбрать ближайшую.
Посчитаем для каждой клетки расстояние до правой нижней по черным клеткам и расстояние до ближайшей белой. Заметим, что для любой белой клетки расстояние до ближайшей белой не больше двух. Теперь разобьем все белые клетки на два множества — те, из которых робот сразу должен идти в правую нижнюю клетку, и те, из которых робот должен идти в соседнюю белую. Когда такое разбиение произведено, ответ вычислить несложно. Записав рекуррентное соотношение для среднего ответа для всех белых клеток, найдем его. Это будет некоторая дробь со знаменателем не больше количества белых клеток. Теперь ответ — это min(расстояние по черным клеткам до правой нижней, расстояние до ближайшей белой + средний ответ для всех белых).
Осталось научиться находить правильное разбиение белых клеток на множества. Отсортируем все белые клетки по критерию (расстояние до правой нижней по черным — расстояние до ближайшей белой). Утверждается, что оптимальное разбиение следующее — из всех клеток некоторого префикса отсортированного массива необходимо идти сразу в правую нижнюю клетку, а из остальных — в ближайшую белую. Этот факт несложно доказывается методом от противного (пусть оптимальное разбиение имеет другой вид; рассмотрим средний ответ для белых клеток, увидим, что некоторые клетки можно переместить из одного множества в другое, не ухудшив ответ, но приведя разбиение к нужному виду).
В итоге решение сводится к следующему. Посчитаем расстояния, которые обсуждались ранее, для всех клеток. Отсортируем белые клетки. Переберем разбиение на множества, каждый раз пересчитывая средний ответ для белых клеток за O(1). Ответ на задачу — минимум из расстояния по черным клеткам и расстояния до ближайшей белой клетки + средний ответ для белых клеток. Если сортировать белые клетки подсчетом, то общая сложность решения будет O(общее количество клеток).
Какая из задач вам показалась наиболее интересной?
Анонс первого квалификационного раунда 19 апреля.
Напоминаем, для того чтобы принять участие в Russian Code Cup, нужно зарегистрироваться на сайте http://russiancodecup.ru/ (регистрация будет открыта до начала третьего квалификационного раунда).
2011 год, Финальный раунд, «B» Обратная задача о черепашке
2011 год, Финальный раунд, «D» Архиватор
2012 год, 2-й квалификационный раунд, «C» Тетраэдр
2012 год, Отборочный раунд, «F» Принц
2012 год, Финальный раунд, «E» Перемешивание колоды
2013 год, Отборочный раунд, «E» Лазеры
2013 год, Финальный раунд, «D» Робот
1) 2011 год, Финальный раунд, «B» Обратная задача о черепашке
Разбор:
В этой задаче требовалось по заданному числу k построить лабиринт, в котором количество путей из левой верхней в нижнюю правую клетку было бы равно k при условии, что разрешается двигаться только вправо и вниз.
Заметим следующее. Пусть у нас есть два лабиринта, в которых количество способов добраться от верхней левой до правой нижней клетки равно a и b соответственно.
Тогда, разместив их параллельно, как показано на рисунке, мы можем получить лабиринт, для которого есть a + b способов добраться из верхней левой до нижней правой клетки. А разместив их последовательно — получить лабиринт, в котором ab путей.
Заметим, что в пустом лабиринте размером 2×2 существует два пути, а в лабиринте размера 1×1 — один путь. Следовательно, разложив число k в двоичную систему счисления и используя описанный метод, можно получить лабиринт с k путями из верхней левой в правую нижнюю клетку.
Пример такого лабиринта для k = 19 приведен на рисунке.
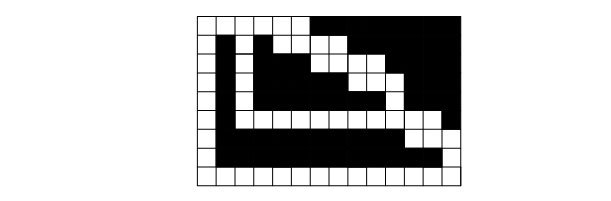
Заметим, что на каждый разряд числа k требуется 5 клеток по горизонтали, а 260 > 1018, поэтому приведенная схема позволяет создать лабиринт размером не более 300×300, что и требуется в условии задачи.
2) 2011 год, Финальный раунд, «D» Архиватор
Разбор:
К этой задаче возможно как минимум два различных подхода: динамическое программирование или жадный алгоритм.
Представим процесс архивации последовательности в виде дерева: каждый символ каждой из промежуточных последовательностей будет вершиной дерева, детьми вершины будут два символа, которые «склеиваются» в процессе архивации в заданный. В листьях записаны исходные числа, а задача состоит в том, чтобы во все промежуточные вершины записать числа, при этом штраф за архивацию равен числу вершин, у которых в детях записаны различные числа.
Решение с помощью динамического программирования устроено следующим образом: в каждой вершине u будем хранить минимальный суммарный штраф p[u][x] для поддерева, если в этой вершине записать число x. Заметим, что в вершине осмысленно записывать только число, которое встречается в одном из листьев в поддереве, поэтому суммарное количество вариантов, которое следует рассмотреть, есть O(n log n).
Пересчет осуществляется следующим образом: рассмотрим вершину u с детьми v и w. Пусть мы планируем записать значение x. Если оба значения p[v][x] и p[w][x] определены, то один из вариантов поставить x в u — это поставить x в обоих детей, цена этого варианта p[v][x] + p[w][x]. Также есть вариант поставить x лишь в одного ребенка. Пусть мы планируем поставить x в v, тогда стоимость этого варианта p[v][x] + minp[w] + 1, где minp[w] — минимальное значение p[w][y] по всем y.
Альтернативой решению с помощью ДП является жадное решение: для каждой вершины будем хранить список всех возможных значений, поставив одно из которых в вершину мы получим минимальный штраф в поддереве. Оказывается, что для того, чтобы найти оптимальное множество для вершины, достаточно пробовать поставить в ее детей лишь оптимальные значения. При этом, если списки оптимальных значений для детей пересекаются, то необходимо взять одно из таких чисел. Если же они не пересекаются, то подойдет любое из значений каждого из детей.
Доказательство корректности приведенного алгоритма оставим в качестве упражнения.
3) 2012 год, 2-й квалификационный раунд, «C» Тетраэдр
Разбор:
Напомню, что тетраэдр — это многогранник, гранями которого являются четыре треугольника (другими словами — треугольная пирамида).
Все начинается с того, что мы перебираем возможные соответствия спичек ребрам тетраэдра. Обозначим искомый тетраэдр как ABCD. У него шесть ребер: AB, AC, AD, BC, BD и CD. Переберем все 6! = 720 вариантов, какая спичка соответствует какому ребру. Теперь осталось проверить, что соответствующий тетраэдр существует.
Как проверить существование тетраэдра? Здесь есть как минимум три решения.
Первое решение основывается на вычислении объема тетраэдра. Самое простое решение — найти формулу для расчета объема тетраэдра по граням. Эта задача сама по себе непростая, приведу здесь формулу:
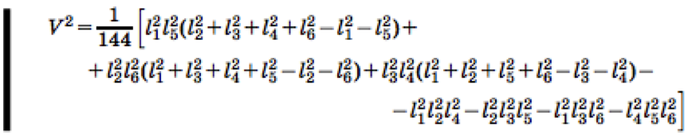
Соответственно, если правая часть равенства оказывается отрицательной или треугольники в гранях построить нельзя (неравенство треугольника), то тетраэдр не сойдется.
Для интересующихся — здесь эта формула выводится.
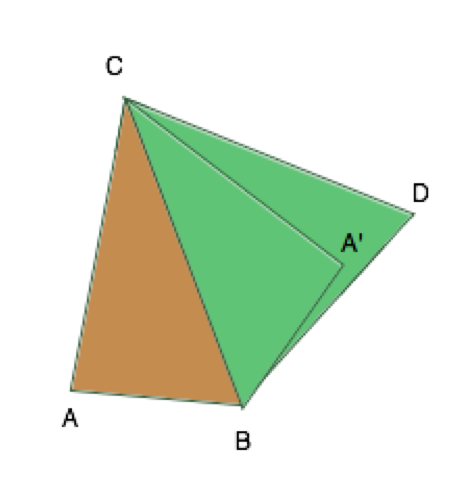
Второй подход к решению задачи — геометрический. Сначала убедимся, что ABC и BCD существуют. Теперь попытаемся сделать тетраэдр. Понятно, что при построении объемной фигуры проблема может возникнуть только с последним ребром — оно может оказаться или слишком длинным, или слишком коротким. Поэтому в этом решении предлагается найти диапазон длины последнего ребра.
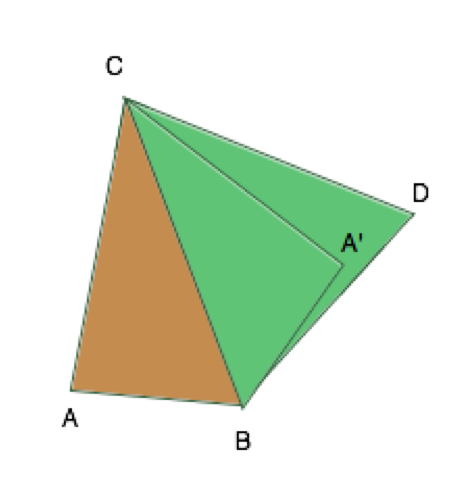
Есть два предельных варианта размещения граней, при которых тетраэдр превращается в плоскую фигуру. Первый — когда грани развернуты друг относительно друга на 180 градусов (CAB и CBD), и вторая — когда они «сложены» и образуют «нулевой угол» (CA’D и CDB). Все допустимые положения граней друг относительно друга находятся в диапазоне между этими граничными. Наибольшей своей длины последнее ребро (A-D) достигает в первом предельном варианте (AD), а наименьшей — в последнем (A’D). Следовательно, тетраэдр будет существовать, если эта длина последнего ребра укладывается в найденный нами диапазон (от A’D до AD).
Для того, чтобы найти расстояние между точками A и D и A’ и D, найдем сначала их координаты, приняв за ноль одну из общих для треугольников вершин, а ось абсцисс проведем через одно из ребер, исходящих из этой вершины. Найти координаты всех остальных вершин в этой системе координат довольно просто: через соотношения сторон и косинусы углов мы определим положения вершин в полярных координатах (угол, расстояние), после чего переведем их в декартову систему координат. Зная координаты вершин, вычислить максимальное и минимальное расстояния между несвязанными вершинами совсем просто.
Программа должна проверять, умещается ли длина оставшейся грани в указанные диапазоны. Если да, то тетраэдр из таких длин «собрать» можно.
Третий способ также геометрический. Сначала необходимо проверить существование всех треугольников с указанными сторонами. Если хотя бы один треугольник не может быть построен по указанным значениям сторон, то тетраэдр также не может быть построен. Для проверки необходимо проверить неравенство невырожденного треугольника: любая из его сторон должна быть строго меньше суммы двух других.
Во многих случаях решение этим и ограничилось; между тем существуют ситуации, когда треугольники с указанными сторонами могут быть построены, а тетраэдр из них собрать невозможно.
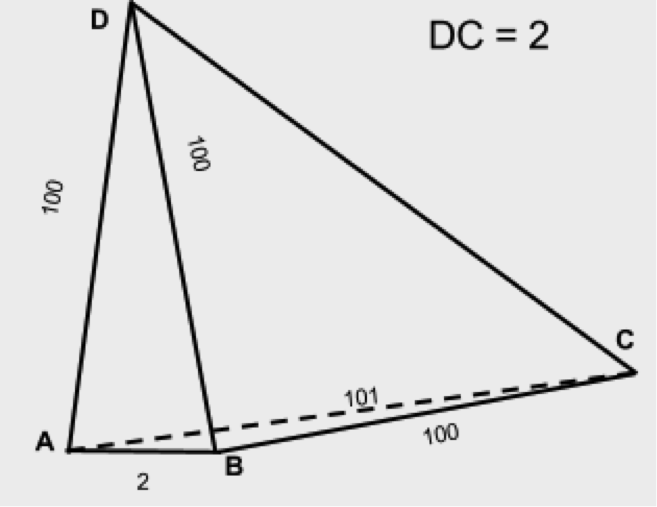
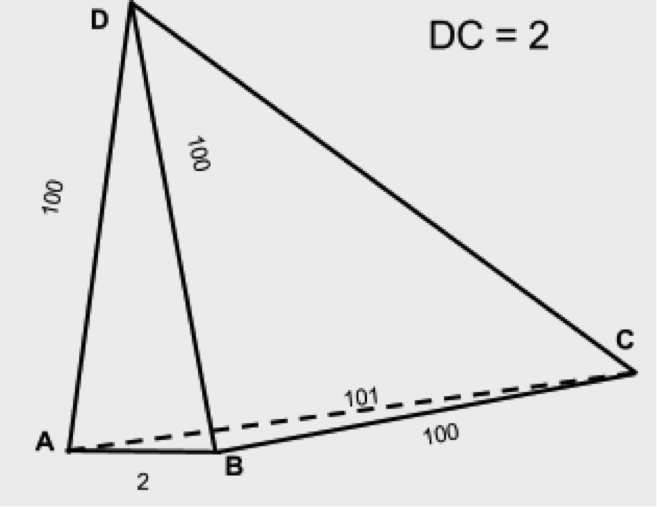
Например, если мы имеем грани (100,100,2,101,100,2), то треугольники (100,100,2) и (101,100,2) формально удовлетворяют неравенству треугольника, но тетраэдр сложить из таких треугольников невозможно. Из рисунка мы видим, что ребро AC почти параллельно AB, значит, расстояние от D до C почти не будет меняться при любом наклоне грани ABD относительно AB, из чего можно заключить, что DB почти перпендикулярно BC. В этом случае DC можно приблизительно оценить как корень из суммы квадратов катетов, то есть DC должно быть приблизительно около 10, а совсем не 2, как мы предположили в условии.
Следовательно, кроме проверки на треугольники в гранях, необходимо выполнить дополнительную проверку на трехгранные углы. Необходимых и достаточных условий существования трехгранного угла два:
- сумма плоских углов трехгранного угла должна быть меньше 360 градусов,
- каждый плоский угол трехгранного угла должен быть меньше суммы двух других плоских углов.
Плоский угол находится через теорему косинусов для треугольника.
Всего было направлено на проверку 1088 решений, из них правильных всего 74 (7%). 8% участников Russian Code Cup QR2 справились с этой задачей. Первое решение пришло от участника с ником AVictor через 30 минут после начала раунда.
4) 2012 год, Отборочный раунд, «F» Принц
Разбор:
В этой задаче необходимо найти минимальное время, за которое принц попадет к принцессе по одномерному коридору, не попав ни в одну ловушку. Известны расписание, размеры и места появления/исчезновения ловушек, а также скорость движения принца. Поскольку коридор одномерный, то двигаться принц может либо по направлению к принцессе, либо от нее, либо никуда не двигаться вообще. Очевидно, существуют ситуации, когда выхода нет, и принц не попадет к принцессе — в этом случае нужно вывести Impossible.
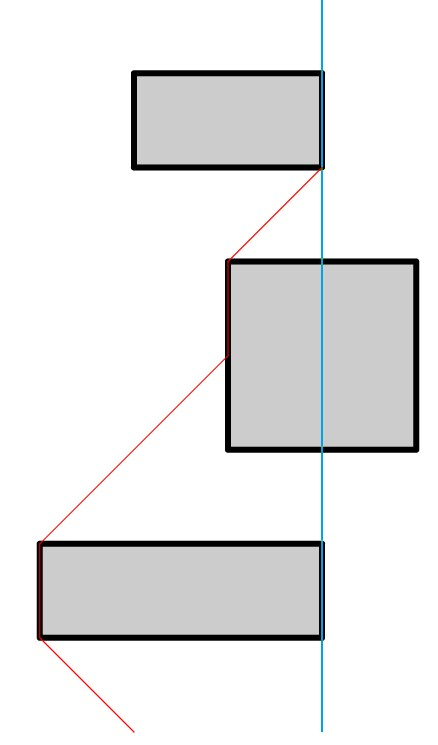
Решение этой задачи стоит начать с того, что изобразить ловушки на плоскости, где координатой x является позиция в коридоре, а координатой y — время. Теперь задачу можно переформулировать в понятиях этой плоскости: требуется попасть из точки (0, 0) в точку (x, y) с минимальным y, при этом разрешено двигаться вертикально вверх (стоять на месте), по диагонали направо вверх и налево вверх (двигаться по коридору) и запрещено заходить в определенные прямоугольники (ловушки). Находиться на границе прямоугольника разрешено.
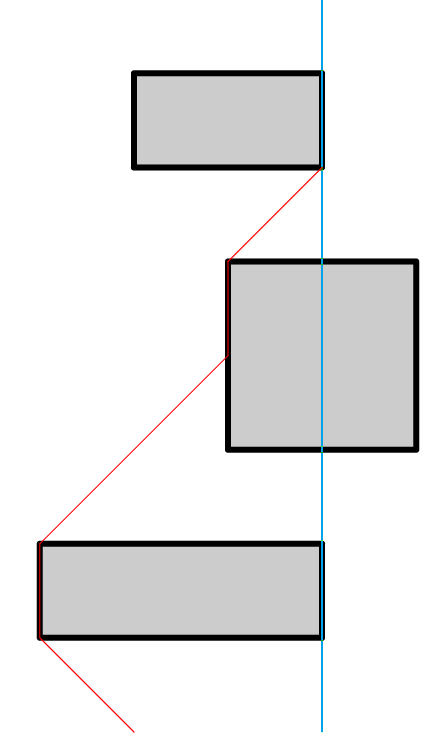
Оптимальный путь в такой задаче будет состоять из множества однотипных частей, каждая из которых будет состоять из движения по одной из диагоналей до координаты, соответствующей границе одного из прямоугольников, с последующим движением вертикально вверх до верхнего угла этого прямоугольника. Таким образом, ключевыми точками являются верхние левые и верхние правые углы каждого прямоугольника и про них необходимо выяснить, можно ли туда попасть.
При движении по диагонали будем поддерживать множество прямоугольников, находящихся над текущей позицией. Так как на границе прямоугольников находиться можно, то прямоугольники, начинающиеся или заканчивающиеся на текущей «коридорной» координате, учитывать не будем. Прямоугольники будем хранить в множестве, упорядоченными по нижнему краю. Такое множество будем называть срезом. Для хранения множества можно использовать структуры данных, подобные красно-черным или декартовым деревьям или очереди с приоритетом. Нижний край нижнего прямоугольника будем называть краем среза. Если срез не содержит прямоугольников, то будем считать его край бесконечностью.
Так как при любом движении увеличивается координата времени, то будем рассматривать углы прямоугольников в порядке неубывания этой координаты. Рассматривая очередной угол, попытаемся двигаться от него по диагонали в обе стороны. Движение осуществляется по координатам, соответствующим границам прямоугольников. Достигая очередной координаты, проверяем, можно ли, двигаясь вертикально вверх, попасть в соответствующий верхний угол какого-либо прямоугольника. Достичь угла можно, если этот угол находится не выше края текущего среза. Также необходимо проверить, что движение не уперлось в край одного из прямоугольников, начинающихся в данной координате. Если удалось достигнуть координаты двери x, то необходимо обновить текущий ответ. Если при движении от одной координаты к другой был превышен край среза, то при переходе был достигнут нижний край прямоугольника, и движение необходимо прекратить.
Поочередно рассмотрев все углы и шагая в обе стороны от каждого из них, найдем минимальный возможный ответ или информацию о том, что дверь не достижима. Описанный алгоритм совершает O(n2 log n) операций, так как необходимо из каждого из O(n) углов пройти по диагонали O(n) различных координат и проверить O(n) прямоугольников. Также для каждого угла приходится совершать O(n log n) операций для поддержания среза, так как необходимо добавлять и удалять из среза O(n) прямоугольников.
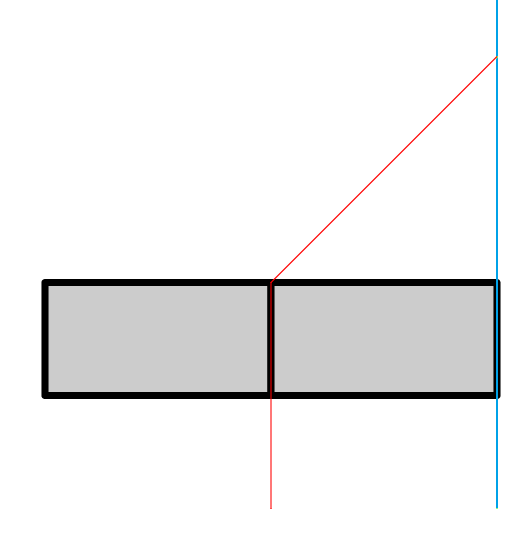
Далее приведены возможные варианты прохождения мимо прямоугольников, которые необходимо не забыть обработать.
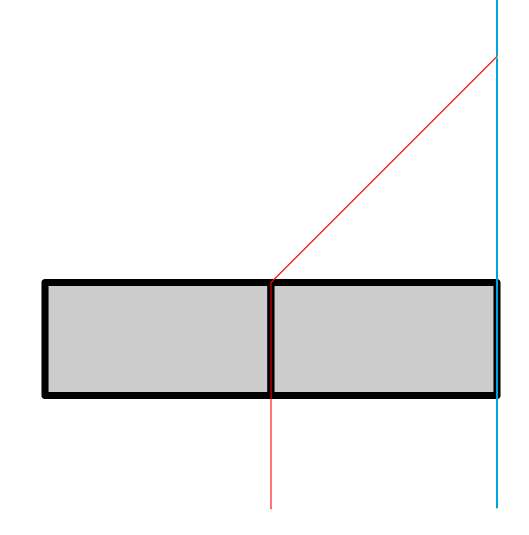
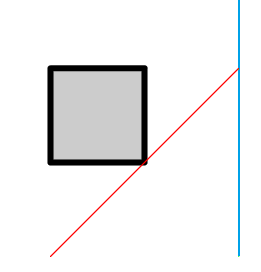
и
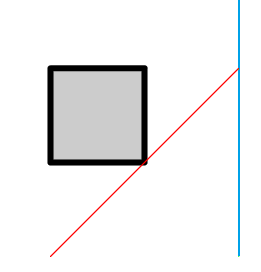
В то же время на следующем тесте невозможно успеть попасть к двери.
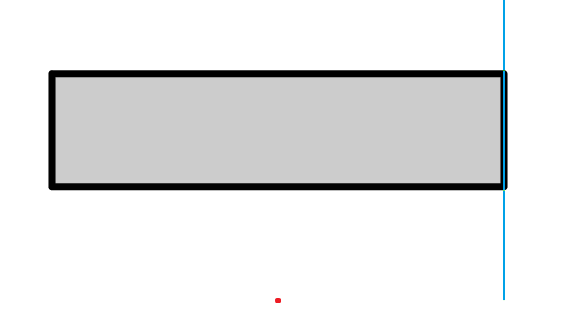
Эта задача тоже не из простых — ее решили всего 23 человека, первым — Куликов Егор на 100:18. Тут стоит отметить Епифанова Владислава, отправившего решение этой задачи, последней для него, за 2 минуты до конца тура. Владислав занял первое место как в квалификации, так и на отборочном туре.
5) 2012 год, Финальный раунд, «E» Перемешивание колоды
Разбор:
О задаче про перемешивание колоды рассказывает Сергей МЕЛЬНИКОВ, студент НИУ ИТМО.
В этой задаче нужно продумать механизм перемешивания колоды, позволяющий за минимальное число перемещений блоков карт из середины в конец колоды идеально ее перемешать (то есть сделать так, чтобы никакие две одинаковые карты не шли друг за другом), либо сообщить, что идеально перемешать колоду невозможно. Изначально колода отсортирована по неубыванию достоинства. Дано количество разных достоинств карт, порядок карт в колоде, количество колод.
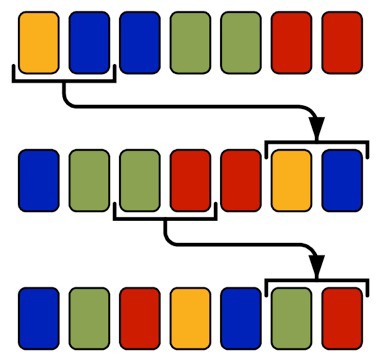
Подробная постановка задачи
Назовем конфликтом ситуацию, в которой две одинаковые карты стоят подряд:
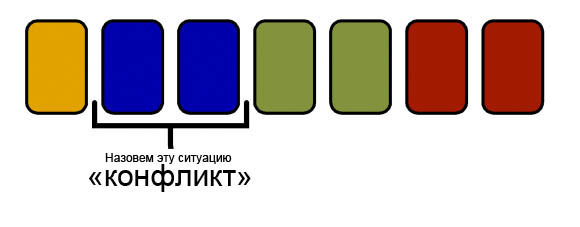
Назовем телом исходную последовательность карт, которую постепенно будем уменьшать, перенося карты в хвост. Хвост будет формироваться таким образом, чтобы карты в нем не образовывали конфликтов.
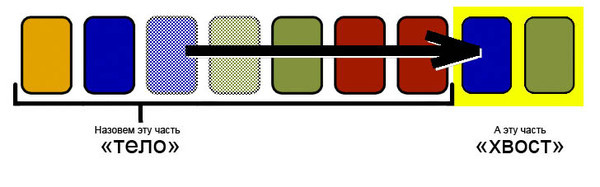
Преобразуем исходную последовательность в последовательность конфликтов и будем работать с новой последовательностью. Будем называть цветом конфликта число, написанное на карточках, его образующих. Каждый раз перенося отрезок карт в конец колоды, будем выбирать его концы внутри конфликтов.
Обозначим число конфликтов через K. Поскольку одна операция перемещения убирает не более двух конфликтов, задачу невозможно решить быстрее чем за ⌈K / 2⌉ операций (здесь и далее в описании встречаются конструкции ⌊…⌋ и ⌈…⌉ — это округление вниз и вверх соответственно).
Обозначим как M максимальное число конфликтов одного цвета и будем называть сами эти конфликты «максимальными». Научимся решать задачу в случае, когда M = ⌈K / 2⌉.
Также напомню, что по условиям задачи колода отсортирована по неубыванию достоинства.
К примеру, в колоде 1122333344 число М будет равно 3 (три конфликта 33), общее число конфликтов – 6. В данном случае M = ⌈K / 2⌉.
В рассматриваемом случае (не примере) есть два варианта:
- K — четное (как в примере). Покрасим все конфликты, предшествующие «максимальным» в цвет A, «максимальные» конфликты в цвет B, а следующие за ним — в цвет C. |A| + |B| + |C| = |K|, следовательно |A| + |C| = |B| = M. В приведенном выше примере цветовая раскраска для 1122333344 будет AABBBC. Будем ликвидировать конфликты парами: сначала пары (B, C), потом, когда таких пар не останется — пары (A, B). Отметим, что хвост будет иметь вид (B, C)* (A, B)*, где * — одно или более повторение. В нашем примере это: 1122333344 (AABBC) ->1122333-4.34 (AAB) -> 1-2333-4.3412 (BB) (дефисы обозначают места, откуда взяты карты перед переносом в хвост. Точка — разделитель тела и хвоста). Очевидно, два конфликта одного цвета подряд не идут. При сопряжении с телом тоже все будет хорошо: если |C| > 0, то последняя карточка со значением C останется на месте, а хвост будет начинаться с B. Если же |C| = 0, то хвост имеет вид (A, B)*, при этом последняя карточка со значением B останется на месте.
- K — нечетное. Применим аналогичную раскраску. Если есть хотя бы одна карточка цвета A, то сведем задачу к предыдущему случаю, добавив в начало виртуальную карточку и A-конфликт. Если есть карточка цвета C, то добавим новую виртуальную карточку и C-конфликт в конец, опять сведя к предыдущему случаю.
Решения для этих случаев оптимальны, так как достигается нижняя граница числа операций ⌈K / 2⌉. Итого, мы умеем оптимально решать задачу, когда число «максимальных» конфликтов составляет половину всех конфликтов (с округлением вверх). Будем называть такой случай базовым.
Теперь классифицируем исходные ситуации по максимальному числу карточек одного достоинства подряд. Будем называть эти карточки максимальными и обозначим их количество как Q.
- Q = 0. Конфликты отсутствуют, ничего делать не надо.
- Если Q > ⌈N / 2⌉, то задача не имеет решения. В этом случае, у нас есть менее Q−1 не максимальных карточек, чего не достаточно для разделения карточек максимального достоинства.
- Q = ⌈N / 2⌉. В этом случае не максимальных карточек хватает, но каждая вторая карточка должна быть максимальной. Покрасив карточки в три цвета получим:
- a A-карточек идущих до максимальных,
- b = Q B-карточек являющихся максимальными
- c C-карточек после максимальных.
- При этом будем считать, что все A- и C-карточки образуют конфликты Рассмотрим следующие случаи:
- a = 0. Следовательно c = N − Q = ⌊N / 2⌋, и тогда b отличается от c не более чем на единицу, то есть мы свели к базовому случаю.
- с = 0. Аналогично предыдущему случаю.
- a > 0, b > 0 Среди А-карточек a − 1 конфликт, среди B: b − 1, среди C: c − 1. (a − 1) + (c − 1) = N − Q − 2, отличается от Q − 1 не более чем на единицу, а это значит, что это базовый случай.
- M < ⌊ ( N + 1) / 2 ⌋. Если можно добавить некоторое количество виртуальных конфликтов (конфликтов между карточками с разными значениями), чтобы задача свелась к базовому случаю, то добавим их и решим как базовый случай.
Теперь будем каждый раз удалять последнюю пару конфликтов, которую можно удалить (два последних конфликта разного цвета) (C1, C2). Если в процессе попадем в базовый случай, то будем решать так, как решаем его. Если больше конфликтов не осталось, то задача решена.
Докажем, что новых конфликтов не возникнет. Рассмотрим цвет последнего конфликта Z, мы будем переносить пары конфликтов (X, Z) пока Z не кончится, при этом на конце останется Z, и получим хвост Z (X1, Z) (X2, Z)…. Если Z-конфликты кончатся, то будет переход на (X, Y) конфликты, то есть пара (Xk, Z) (Xk+1, Y), при Xk+1 ≠ Z.
При переходе к базовому случаю конфликтов не возникнет, потому что после переноса пары (X, Z) ни X, ни Z не могут стать максимальными (M). Так как M ≠ Z, то либо Z кончились и конфликта (X, Z) (Z, ...) не возникнет, либо Z находится после M, то есть получим продолжение (X, Z) (M, Z).
Так как мы на каждом шаге удаляем пару конфликтов, либо используем базовый случай, то построенное решение оптимально и работает за ⌈K / 2⌉ операций.
Можно заметить, что нет необходимости хранить информацию о том, какие числа и в каком порядке записаны в хвосте, поскольку там нет конфликтов. Последовательность значений можно поддерживать при помощи декартового дерева по неявному ключу, при этом суммарное время работы составит O(N log N). Также, если в какой-то момент мы определяем, что в конце тела нет конфликтов, то можно уменьшить длину тела и, соответственно, увеличить хвост. Можно рассмотреть все случаи, когда происходит перемещение отрезка, и убедиться, что тело всегда будет иметь вид: префикс исходного массива с не более чем двумя вырезанными подотрезками. Основываясь на этом факте, можно реализовать решение за O(n), но для решения данной задачи в данных ограничениях этого не требуется.
Задачу «Перемешивание карт» решил только Евгений КАПУН
6) 2013 год, Отборочный раунд, «E» Лазеры
Разбор:
Основная идея решения — двоичный поиск по ответу. Зафиксируем максимальный угол отклонения α и проверим существование решения с таким ответом. Для этого сведем задачу к поиску пути в графе.
Обозначим точки, заданные в условии, как P1, P2, ..., Pn. Построим граф из n(n — 1) вершин, где каждая вершина — это упорядоченная пара различных точек. Проведем ребра из пары (i, j) в пару (j, k) в том случае, если угол между векторами PiPj и PjPk не превосходит α. В построенном графе не более чем n3 ребер. Теперь, если в таком графе существует путь из вершины вида (1, i) в вершину вида (j, 1), то при таком α эксперимент осуществить можно. Проверять существование пути можно с помощью любого алгоритма поиска пути в графе.
Таким образом, одна итерация двоичного поиска работает за O(n3), а значит, весь алгоритм можно реализовать за O(n3 log(1/ε)) или, если заметить, что пространство поиска на самом деле дискретно (нас интересуют лишь не более чем n3 углов), то этот алгоритм можно реализовать за O(n3 log(n3)).
7) 2013 год, Финальный раунд, «D» Робот
Разбор:
В данной задаче необходимо было найти матожидание длины кратчайшего пути из одного угла поля в другой. При этом некоторые клетки поля были покрашены в белый цвет, и при попадании робота на такую клетку он переставлялся в случайную белую клетку поля.
Разберемся подробнее, как устроена оптимальная стратегия выбора пути. Для каждой клетки поля можно посчитать матожидание количества ходов, необходимых для того, чтобы попасть в правую нижнюю клетку. При этом ответ будет соответствовать расстоянию, которое записано в левой верхней клетке. Как же вычислить эти значения? Рассмотрим конкретную клетку и все соседние с ней. Если соседняя клетка покрашена в черный цвет, то ответ для клетки будет как минимум (1 + значение, которое записано в соседней клетке). Если же у клетки есть белый сосед, то ответ для нее равен как минимум (1 + среднее арифметическое ответов для всех белых клеток).
Понятно, что если робот два раза попадает в одну и ту же клетку, то существует оптимальная стратегия, в которой следующий ход в обоих случаях одинаковый. Если это не так, то на каком-то из ходов робот поступил неправильно и пошел в клетку с большим матожиданием количества ходов до конца, а значит, стратегию можно улучшить. Есть два принципиально разных действия, которые может сделать робот, находясь в некоторой клетке. Он может пойти сразу в правый нижний угол по черным клеткам (если такой путь существует), а может пойти в некоторую белую клетку. Очевидно, что среди всех белых клеток, в которые можно пойти, следует выбрать ближайшую.
Посчитаем для каждой клетки расстояние до правой нижней по черным клеткам и расстояние до ближайшей белой. Заметим, что для любой белой клетки расстояние до ближайшей белой не больше двух. Теперь разобьем все белые клетки на два множества — те, из которых робот сразу должен идти в правую нижнюю клетку, и те, из которых робот должен идти в соседнюю белую. Когда такое разбиение произведено, ответ вычислить несложно. Записав рекуррентное соотношение для среднего ответа для всех белых клеток, найдем его. Это будет некоторая дробь со знаменателем не больше количества белых клеток. Теперь ответ — это min(расстояние по черным клеткам до правой нижней, расстояние до ближайшей белой + средний ответ для всех белых).
Осталось научиться находить правильное разбиение белых клеток на множества. Отсортируем все белые клетки по критерию (расстояние до правой нижней по черным — расстояние до ближайшей белой). Утверждается, что оптимальное разбиение следующее — из всех клеток некоторого префикса отсортированного массива необходимо идти сразу в правую нижнюю клетку, а из остальных — в ближайшую белую. Этот факт несложно доказывается методом от противного (пусть оптимальное разбиение имеет другой вид; рассмотрим средний ответ для белых клеток, увидим, что некоторые клетки можно переместить из одного множества в другое, не ухудшив ответ, но приведя разбиение к нужному виду).
В итоге решение сводится к следующему. Посчитаем расстояния, которые обсуждались ранее, для всех клеток. Отсортируем белые клетки. Переберем разбиение на множества, каждый раз пересчитывая средний ответ для белых клеток за O(1). Ответ на задачу — минимум из расстояния по черным клеткам и расстояния до ближайшей белой клетки + средний ответ для белых клеток. Если сортировать белые клетки подсчетом, то общая сложность решения будет O(общее количество клеток).
Какая из задач вам показалась наиболее интересной?
Анонс первого квалификационного раунда 19 апреля.
