
В конце концов я должен был к этому прийти. Когда-то я опубликовал статью «Я написал быструю хеш-таблицу», а потом ещё одну — «Я написал ещё более быструю хеш-таблицу». Теперь я завершил работу над самой быстрой хеш-таблицей. И под этим я подразумеваю, что реализовал самый быстрый поиск по сравнению со всеми хеш-таблицами, какие мне только удалось найти. При этом операции вставки и удаления также работают очень быстро (хотя и не быстрее конкурентов).
Я использовал хеширование по алгоритму Robin Hood с ограничением максимального количества наборов. Если элемент должен быть на расстоянии больше Х позиций от своей идеальной позиции, то увеличиваем таблицу и надеемся, что в этом случае каждый элемент сможет быть ближе к своей желаемой позиции. Похоже, такой подход действительно хорошо работает. Величина Х может быть относительно невелика, что позволяет реализовать некоторые оптимизации внутреннего цикла поиска по хеш-таблице.
Если вы хотите только попробовать её в работе, то можете скачать отсюда. Либо пролистайте вниз до раздела «Исходный код и использование». Хотите подробностей — читайте дальше.
Тип хеш-таблицы
Существует много типов хеш-таблиц. Для своей я выбрал:
- Открытую адресацию.
- Линейное размещение.
- Хеширование Robin Hood.
- Количество слотов — простое число (но я реализовал возможность использовать для этой цели числа, являющиеся степенями двойки).
- Ограничение максимального количества наборов.
Я считаю, что последний пункт — новинка в сфере хеш-таблиц. Это главная причина высокой производительности моего решения. Но сначала я хотел бы рассказать о предыдущих пунктах.
Открытая адресация означает, что хеш-таблица использует в качестве хранилища данных непрерывный массив. Это не аналог std::unordered_map, когда каждый элемент находится в отдельной куче (heap).
Линейное размещение означает, что если вы пытаетесь вставить элемент в массив, а текущий слот уже заполнен, то вы просто переходите к следующему слоту. Если и он тоже заполнен, то берётся следующий слот, и так далее. У этого простого подхода есть известные недостатки, но я считаю, что они исправляются с помощью ограничения максимального количества наборов.
Хеширование Robin Hood означает, что при линейном размещении вы пытаетесь расположить каждый элемент как можно ближе к его идеальной позиции. Это делается с помощью перемещения окружающих элементов при вставке или удалении какого-то элемента. Принцип такой: берём из богатых элементов (rich elements) и передаём в бедные элементы (poor elements). Отсюда и взялось название Robin Hood. Богатым называется элемент, получивший слот поблизости от своей идеальной точки вставки (insertion point). Бедный элемент находится далеко от идеальной точки вставки. Вставляя новый элемент, вы отсчитываете, насколько далеко он находится от идеальной позиции. Если дальше, чем текущий элемент, то вы ставите новый на место текущего, а затем уже для него пытаетесь найти новое место.
Количество слотов — простое число: размер массива, лежащего в основе хеш-таблицы, равен простому числу. Это означает, что он может вырасти, например, с 5 слотов до 11, затем до 23, до 47 и так далее. Когда нужно найти точку вставки, то для присваивания слоту значения хеша элемента используется оператор по модулю (modulo operator). Другой вариант — делать размер массива равным степени двойки. Ниже мы поговорим о том, почему по умолчанию я использую простые числа и когда целесообразно применять оба варианта.
Ограничение максимального количества наборов
C основами разобрались, давайте теперь обсудим моё решение: ограничение максимального количества слотов, в которых таблица будет выполнять поиск, после чего плюнет и увеличит размер массива.
Сначала идея была в том, чтобы сделать это количество очень небольшим, например равным 4. То есть при вставке я сначала пробую идеальный слот, если не получается — то обращаюсь к следующему, затем к следующему, затем к следующему, и если все они оказываются заполнены, то я увеличиваю таблицу и снова пытаюсь вставить элемент. Это прекрасно работает на маленьких таблицах. Но при вставке случайного значения в большую таблицу я всё время буду терпеть неудачу с этими четырьмя наборами, мне придётся увеличивать размер таблицы, даже если она по большей части пустая.
В конце концов я обнаружил, что при верхней границе, равной log2(n), где n — количество слотов в таблице, перераспределение (reallocate) выполняется, только когда она заполнена примерно на 2/3. Это при вставке случайного значения. А если вставлять последовательные значения, то можно заполнить таблицу целиком, и только тогда она будет перераспределена.
Но несмотря на эмпирически найденный порог в 2/3, время от времени перераспределение запускалось при 60%-м заполнении таблицы. Изредка — даже при 55%-м. Поэтому я присвоил max_load_factor таблицы значение 0,5. Это означает, что таблица будет увеличиваться при заполнении в 50 %, даже если не был достигнут предел по количеству наборов. Я сделал это для того, чтобы вы могли доверить таблице перераспределение, когда вы действительно увеличиваете её размер: если вы вставляете тысячу элементов, затем пару из них удаляете, а потом снова вставляете столько же, то можете быть почти полностью уверены, что таблица не будет перераспределена. У меня нет точной статистики, но я прогнал простой тест, в котором построил тысячи таблиц всевозможных размеров и заполнил их случайными числами. В сумме я выполнил вставку сотен миллиардов чисел, и лишь один раз было перераспределение при коэффициенте заполнения (load factor) меньше 0,5 (таблица увеличилась при заполнении 48 %). Так что вы можете доверять такому механизму: он очень-очень-очень редко перераспределяет, когда вы этого не ждёте.
В общем, если вам не нужно контролировать увеличение таблицы, свободно присваивайте max_load_factor значение повыше. Без опаски ставьте вплоть до 0,9: высокая скорость выполнения всех операций обеспечивается комбинацией Robin Hood и ограничения на количество наборов. Но не присваивайте значение 1,0: может возникнуть ситуация, когда при вставке начнётся перемещение каждого элемента таблицы, чтобы заполнить последний оставшийся слот. Например, все слоты, в которых хочет быть последний элемент, уже заняты, за исключением последнего пустого. Тогда вы вставляете элемент в первый слот, в котором он хочет находиться, но тот уже занят. Вам придётся переместить существующий элемент во второй слот, оттуда выселить элемент в третий, и так по цепочке до конца таблицы. В результате вы получите таблицу, в которой все элементы, за исключением самого первого, находятся в одном слоте от своих идеальных позиций. Поиск всё ещё будет выполняться быстро, но последняя вставка займёт много времени. Если же у вас окажется несколько свободных слотов поблизости, то вставляемый элемент передвинет не так много соседей.
Если задать max_load_factor такое низкое значение, что предел по количеству наборов никогда не будет достигнут, то зачем вообще что-то ограничивать? Благодаря этому ограничению можно реализовать тонкую оптимизацию: допустим, вы перехешировали таблицу, чтобы получить 1000 слотов. В моём случае таблица вырастет до 1009, это ближайшее простое число. Двоичный логарифм 1009 округлённо равен 10, так что я ограничиваю количество наборов десятью. Теперь применим хитрость: вместо массива на 1009 слотов сделаем массив на 1019. Но все остальные операции хеширования будут считать, что у нас всего 1009 слотов. Теперь, если два элемента хешируются в индекс 1008, то я могу перейти в конец и вставить в индекс 1009. Мне не нужно проверять диапазон изменения индексов (bounds checking), потому что ограничение количества наборов не даст мне выйти за индекс 1018. Если же у меня будет 11 элементов, которые хотят попасть в последний слот, то таблица увеличится и все эти элементы захешируются в разные слоты. Благодаря отсутствию граничной проверки у меня получаются компактные внутренние циклы. Вот как выглядит функция поиска:
iterator find(const FindKey & key)
{
size_t index = hash_policy.index_for_hash(hash_object(key));
EntryPointer it = entries + index;
for (int8_t distance = 0;; ++distance, ++it)
{
if (it->distance_from_desired < distance)
return end();
else if (compares_equal(key, it->value))
return { it };
}
}По сути, это линейный поиск. Код прекрасно преобразуется в ассемблер. Такой подход лучше простого линейного размещения по двум причинам:
- Нет проверки диапазона изменения индексов. Пустые слоты имеют значение
distance_from_desired, равное –1, так что это аналогично поиску другого элемента. - В цикле выполняется не больше log2(n) итераций. Обычно при поиске в хеш-таблицах худшая временная сложность равна O(n). В моей таблице — O(log n). Это серьёзная разница. Особенно с учётом того, что при линейном размещении предпочтительнее худший вариант, поскольку элементы склонны к группированию.
Мои накладные расходы по памяти — 1 байт на элемент. Я храню distance_from_desired в int8_t. То есть при выравнивании типа (alignment of the type) вставляемого элемента будет плюсоваться (padded out) 1 байт. Так что если вы вставляете целочисленные значения, то 1 байт получит ещё 3 байта паддинга, в результате выйдет 4 байта накладных расходов на каждый элемент. Если вы вставляете указатели, то паддинг будет уже 7 байтов, получаем 8 байтов накладных расходов. Для решения этой проблемы я рассматриваю вариант с изменением схемы использования памяти, но опасаюсь, что тогда у меня на каждый поиск будет два промаха кеша (cache misses) вместо одного. Так что накладные расходы по памяти — 1 байт на элемент + паддинг. И при значении max_load_factor по умолчанию 0,5 ваша таблица будет заполняться только на 25—50 %, так что общие накладные расходы ещё выше. Напомню, что ради экономии памяти можно без боязни увеличивать max_load_factor до 0,9, это приведёт лишь к незначительному снижению скорости.
Производительность поиска
Не так-то просто выяснить производительность хеш-таблиц. Как минимум нужно измерять скорость в таких ситуациях:
- Поиск элемента, находящегося в таблице.
- Поиск элемента, отсутствующего в таблице.
- Вставка группы случайных чисел.
- Вставка группы случайных чисел после вызова
reserve(). - Удаление элементов.
И каждую из этих ситуаций нужно прогонять с разными ключами и значениями разных размеров. В качестве ключа я использую целочисленное или строковое значение, а типы-значения размером 4, 32 и 1024. Предпочитаю целочисленные значения, потому что со строковыми вы по большей части измеряете накладные расходы хеш-функции и оператора сравнения, одинаковые для всех хеш-таблиц.
Нужно тестировать поиск как при наличии элемента в таблице, так и при его отсутствии, потому что в этих случаях производительность может кардинально различаться. Например, я столкнулся с непростой ситуацией, когда вставил все числа от 0 до 500 000 в google::dense_hash_map (не случайные числа), а потом выполнил поиск отсутствующего элемента. Неожиданно оказалось, что хеш-таблица работает в 500 раз медленнее, чем обычно. Это крайний случай — использование степени двойки для задания размера таблицы. Вероятно, нужно было проводить измерения со случайными числами и с последовательными, но тогда получилось бы слишком много графиков. Так что я ограничусь только случайными числами, они избавляют от возникновения неудачных ситуаций с производительностью из-за специфических паттернов.
Первый график — поиск элемента, присутствующего в таблице:
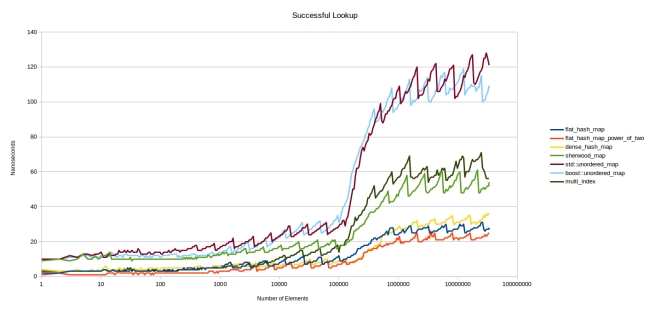
Графики расположены довольно плотно. flat_hash_map — это моя новая хеш-таблица. flat_hash_map_power_of_two — та же самая таблица, но размер массива определяется степенью двойки, а не простым числом. Как видите, второй вариант заметно быстрее, причину я объясню потом. dense_hash_map — это google::dense_hash_map, самая быстрая из найденных мной хеш-таблиц. sherwood_map — старая таблица из «Я написал более быструю хеш-таблицу». К моему конфузу, она показала посредственные результаты… std::unordered_map и boost::unordered_map — всё понятно из названий. multi_index — это boost::multi_index.
Немного обсудим этот график. Ось Y — количество наносекунд, затраченных на поиск одного элемента. Я использовал Google Benchmark, который за полсекунды раз за разом вызывает функцию table.find(), а потом подсчитывает, сколько раз он смог это сделать. Общая длительность итераций делится на их количество, получаются наносекунды. Все искомые ключи присутствуют в таблице. Для оси Х я взял логарифмическую шкалу, потому что она хорошо описывает изменение производительности. К тому же такая шкала позволяет оценить производительность для таблиц разных размеров: если вас интересуют маленькие таблицы, то смотрите на левую часть графика.
Сразу бросается в глаза зубчатость графиков. Дело в том, что все таблицы имеют разную производительность в зависимости от текущего коэффициента заполнения (load factor), то есть степени заполнения. При 25 % поиск будет выполняться быстрее, чем при 50 %: чем больше заполнена таблица, тем больше возникает коллизий хешей. Стоимость поиска растёт, и в какой-то момент таблица решает, что она заполнилась слишком сильно и пора перераспределяться, что снова приводит к ускорению поиска.
Это было бы очевидно, если бы я вывел графики коэффициента заполнения для каждой таблицы. Также вы бы сразу увидели, что нижние графики получены при max_load_factor, равном 0,5, а верхние — при 1,0. Сразу возникает вопрос: были бы таблицы из верхних графиков быстрее нижних при том же значении — 0,5? Были бы, но очень незначительно. Далее мы рассмотрим эту ситуацию более развёрнуто. На приведённом графике видно, что нижняя точка верхних графиков, когда таблицы только что перераспределились и имеют коэффициент заполнения чуть больше 0,5, расположена гораздо выше верхней точки нижних графиков прямо перед перераспределением, из-за того что их коэффициент заполнения приближается к 0,5.
Также вы видите, что в левой части все графики относительно плоские. Причина в том, что таблицы полностью отправляются в кеш. Только когда данные перестают помещаться в кеше L3, графики заметно расходятся. Я считаю это большой проблемой. На мой взгляд, правая часть графиков гораздо точнее отражает ситуацию, чем левая: вы получите результаты аналогично левой части только тогда, когда искомый элемент уже находится в кеше.
Поэтому я попытался придумать тест, который показал бы скорость работы таблицы, не находящейся в кеше. Я создал столько таблиц, чтобы они не помещались в L3, и использовал разные таблицы для каждого искомого элемента. Допустим, я хочу измерить скорость работы таблицы, содержащей 32 элемента по 8 байтов. Размер моего кеша L3 — 6 Мб, так что в него помещается примерно 25 тыс. таких таблиц. Чтобы удостовериться, что таблицы в кеше отсутствуют, я создал их с запасом — 75 тыс. штук. И каждый поиск выполнялся в отдельной таблице.
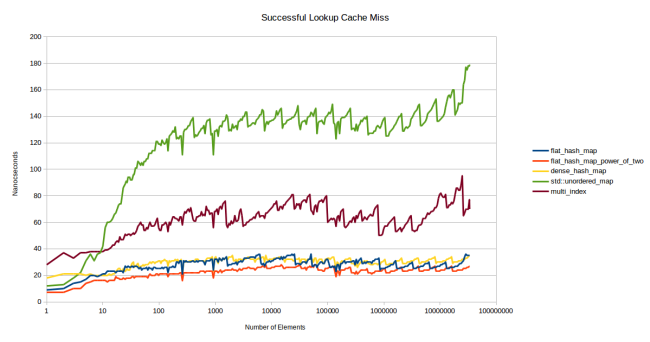
Я убрал пару линий, потому что они были малоинформативны. boost::unordered_map и std::unordered_map обычно демонстрируют одинаковую производительность, и никому нет дела до моей старой медленной таблицы sherwood_map. Теперь у нас остались: std::unordered_map в качестве обычного контейнера на базе узлов (node based container), boost::multi_index в качестве быстрого контейнера на базе узлов (думаю, что std::unordered_map может быть не менее быстрым), google::dense_hash_map в качестве быстрого контейнера с открытой адресацией (open addressing container) и мой новый контейнер в двух версиях — на основе простых чисел и степеней двойки.
В новом бенчмарке графики сразу начали сильно различаться. Паттерн, который проявился на графике первого бенчмарка, на графике второго бенчмарка стал заметен очень рано, начиная с 10 элементов. Впечатляет: все таблицы демонстрируют стабильную производительность в очень большом диапазоне количества элементов.
Давайте посмотрим графики неудачного поиска — то есть поиска элемента, отсутствующего в таблице.
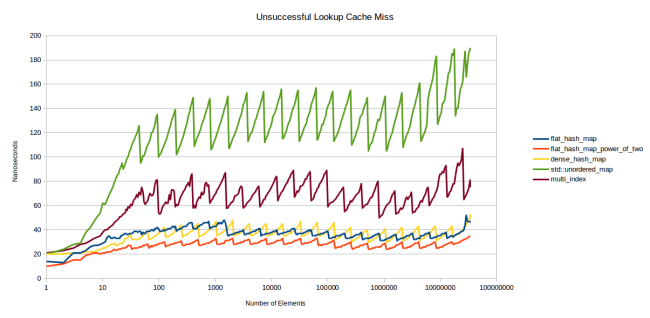
Зубчатость проявляется ещё сильнее, коэффициент заполнения играет заметную роль. Чем сильнее заполнена таблица, тем больше элементов приходится просматривать, прежде чем система решит, что элемент отсутствует. Но мне очень нравятся результаты моей таблицы: похоже, ограничение количества наборов работает. Моя таблица демонстрирует более стабильную производительность, чем другие.
Эти графики убедили меня, что моя новая таблица — большой шаг вперёд. Красная линия показывает работу моей таблицы, сконфигурированной так же, как dense_hash_map: max_load_factor 0,5, а выбор для определения размера степени двойки позволяет помещать хеш в слот просто по младшим битам. Единственное большое отличие: моя таблица использует дополнительный байт для хранения (плюс паддинг) на каждый слот, то есть потребляет чуть больше памяти, чем dense_hash_map.
При этом моя таблица не уступает по скорости даже при использовании простых чисел для определения размера таблицы. Давайте поговорим об этом подробнее.
Простые числа или степень двойки
Поиск элемента в таблице проходит через три дорогостоящих этапа:
- Хеширование ключа.
- Размещение ключа в слоте.
- Получение памяти для этого слота.
Этап 1 может быть дёшев, если ключ — целое число: просто бросьте его в size_t. Но при ключах других типов, например строковых, этап будет дороже.
Этап 2 — целое число по модулю (integer modulo).
Этап 3 — разыменование указателя. В случае с std::unordered_map это разыменование нескольких указателей.
Может показаться, что если у вас не слишком медленная хеш-функция, то этап 3 получается самым дорогим из всех. Но если у вас нет промахов кеша при каждом одиночном поиске, то, скорее всего, самым дорогим этапом окажется второй. Целое число по модулю обрабатывается медленно даже на мощном железе. Согласно данным Intel, это требует от 80 до 95 циклов.
Это главная причина, по которой действительно быстрые хеш-таблицы обычно используют степень двойки для определения размера массива. Потому что потом вам будет достаточно убирать старшие биты, что можно делать в один цикл.
Но у степени двойки есть большой недостаток: немало паттернов вводимых данных создают многочисленные коллизии хешей при использовании степени двойки. Вот график второго бенчмарка, но в этот раз я не использовал случайные числа:
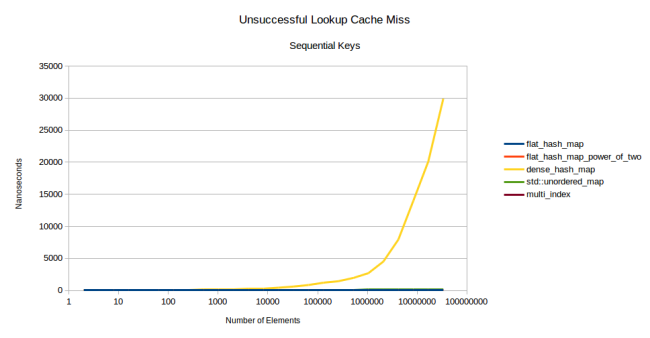
Да, всё верно: google::dense_hash_map ушла в стратосферу. Для этого достаточно было дать ей набор чисел по порядку: [0, 1, 2, …, n – 2, n – 1]. Если сделать это и поискать ключ, которого нет в таблице, то поиск будет крайне медленным. Если ключ есть, то всё нормально, работает быстро. При этом разница в производительности между удачным и неудачным поиском может достигать тысячи крат.
Ещё один пример проблемы из-за степени двойки: стандартная хеш-таблица в Rust стала демонстрировать квадратичное поведение (quadratic) при вставке ключей из одной таблицы в другую. Так что использование степени двойки может привести к неприятным сюрпризам.
Так произошло, что моя таблица избежала всех этих проблем благодаря ограничению количества наборов. Не было даже ненужных перераспределений. Но это не означает, что моя таблица неуязвима для побочных эффектов использования степени двойки. Например, как-то я столкнулся с тем, что при вставке указателей в такую таблицу некоторые слоты постоянно пустовали. Причина в том, что в моей программе кучи были выделены с 16-байтным выравниванием, при этом я использовал хеш-функцию, которая по отношению к указателю просто выполняла reinterpret_casted в size_t. Из-за этого в таблице использовалась лишь одна шестнадцатая всех слотов. Вы можете столкнуться с той же проблемой при использовании степени двойки в моей хеш-таблице.
Все эти проблемы решаемы, если вы позаботитесь о выборе хеш-функции, которая подходит для вводимых вами данных. Но это не слишком удобно: приходится быть настороже при использовании хеш-таблицы. Иногда с этим нет проблем, но иногда не хочется заморачиваться. Хочется, чтобы просто работало, и без неожиданных тормозов. Поэтому я решил в своей таблице по умолчанию использовать размер на основе простых чисел (а степень двойки задаётся опционально).
Почему с простыми числами нет проблем? Не могу объяснить с точки зрения математики, но интуиция подсказывает, что у них нет общих делителей с другими числами, всегда будут разные остатки. Допустим, я использую степень двойки, в моей таблице 32 слота, и я пытаюсь вставить указатели с 16-байтным выравниванием (то есть все мои числа кратны 16). Теперь при поиске слота в таблице с помощью целого числа по модулю я получу только два возможных слота: 0 или 16. Поскольку 32 кратно 16, вы просто не можете получить других значений. Если же взять размер на основе простого числа, то этой проблемы не возникнет. Допустим, у меня 37 слотов, тогда при всех делениях с кратностью 16 я смогу использовать все 37 слотов.
Как можно решить проблему низкой производительности вычисления целого числа по модулю? Я позаимствовал трюк из boost::multi_index: заставил все числа по модулю использовать статическую константу (compile time constant). Я не разрешаю брать в качестве размера таблицы любые возможные простые числа. Я сделал специальную подборку чисел, которая и применяется при увеличении таблиц. Также я сохраняю индекс числа из вашей таблицы. Когда для присвоения слоту хеш-значения нужно вычислить целое число по модулю, выполняется вот что:
switch(prime_index)
{
case 0:
return 0llu;
case 1:
return hash % 2llu;
case 2:
return hash % 3llu;
case 3:
return hash % 5llu;
case 4:
return hash % 7llu;
case 5:
return hash % 11llu;
case 6:
return hash % 13llu;
case 7:
return hash % 17llu;
case 8:
return hash % 23llu;
case 9:
return hash % 29llu;
case 10:
return hash % 37llu;
case 11:
return hash % 47llu;
case 12:
return hash % 59llu;
//
// ... ещё варианты
//
case 185:
return hash % 14480561146010017169llu;
case 186:
return hash % 18446744073709551557llu;
}
Каждый из вариантов — целое число по модулю на основе статической константы. Чем это хорошо? Если использовать константу, то компилятор применит кучу оптимизаций для ускорения вычисления. Для каждого из вариантов вы получаете кастомный ассемблерный код, который будет работать гораздо быстрее, чем целое число по модулю. Выглядит несколько безумно, но даёт огромный прирост скорости.
Вы можете наблюдать разницу на вышеприведённом графике: при использовании простых чисел скорость чуть ниже, но всё равно высокая по сравнению с другими хеш-таблицами, к тому же мы получаем защиту от большинства проблем. Конечно, это не панацея. Если вас сильно это беспокоит, то можете прибегнуть к std::map со строгим ограничением верхней границы. Однако дело в том, что при использовании степени двойки риск куда выше, и приходится проявлять осторожность. В случае же с простыми числами вы нарвётесь на проблему, только если специально создадите ключи с подвохом.
Это подводит нас к вопросу о безопасности. На хеш-таблицу можно провести умную атаку с помощью ключей, которые все конфликтуют друг с другом. Как это провернуть? Если вы знаете, что веб-сайт использует во внутренних кешах хеш-таблицу, то можете составить такие запросы к сайту, которые все будут конфликтовать в этой таблице. Таким образом можно сильно замедлить работу внутреннего кеша веб-сервера с вероятностью положить сайт. Например, если вы знаете, что использует dense_hash_map, у которой проблемы с последовательными числами, то можно просто последовательно запрашивать сайты в надежде, что это загадит их кеши.
Надо сказать, что настройка максимального количества наборов в моей таблице не даёт злоумышленникам заполнить её плохими ключами. Но тут возникает новый источник угрозы: если вы знаете, какой набор простых чисел используется в моей таблице, то вы можете вставить ключи в таком порядке, чтобы таблица постоянно упиралась в ограничение по наборам и постоянно перераспределялась. Это приведёт к исчерпанию памяти на сервере. Уязвимость закрывается с помощью кастомной хеш-функции, но я не буду советовать, что вам искать. Могу лишь сказать, что если используете хеш-таблицу в окружении, где пользователи могут вставлять ключи, то откажитесь от std::hash в качестве хеш-функции, поищите функцию с сохранением текущего состояния (stateful), поведение которой нельзя прогнозировать с течением времени. С другой стороны, если вы не думаете, что среди ваших пользователей будут злоумышленники, то спокойно используйте мою таблицу в версии с простыми числами.
Но, допустим, вы знаете, что ваша хеш-функция возвращает хорошо распределённые числа, и у вас редко могут возникать коллизии даже при использовании степени двойки. Тогда пускайте в дело вторую версию моей таблицы. Для этого достаточно с помощью typedef определить тип hash_policy в объекте хеш-функции. Я решил поместить эту настройку в объект, потому что именно здесь можно выяснить качество возвращаемых ключей.
Итак, вы поместили typedef в свой объект кастомной хеш-функции:
struct CustomHashFunction
{
size_t operator()(const YourStruct & foo)
{
// ваша хеш-функция
}
typedef ska::power_of_two_hash_policy hash_policy;
};
// далее:
ska::flat_hash_map<YourStruct, int, CustomHashFunction> your_hash_map;В вашей хеш-функции задаём для hash_policy тип ska::power_of_two_hash_policy. После этого flat_hash_map переключится на использование степени двойки. Если в данном случае вам подходит std::hash, то можете взять тип power_of_two_std_hash, который просто вызывает std::hash, но с применением power_of_two_hash_policy:
ska::flat_hash_map<K, V, ska::power_of_two_std_hash<K>> your_hash_map;В любом случае вы можете получить ещё более быструю хеш-таблицу, если знаете, что у вас будет мало коллизий.
Производительность вставки и удаления
После такого отвлечения на теорию давайте вернёмся обратно к производительности моей таблицы. Ниже приведён график, на котором отражена производительность при вставке элемента. Я измерял, сколько времени уходит на вставку N элементов, и делил время на их количество. График отражает скорость работы таблицы без вызова reserve() перед вставкой элемента:
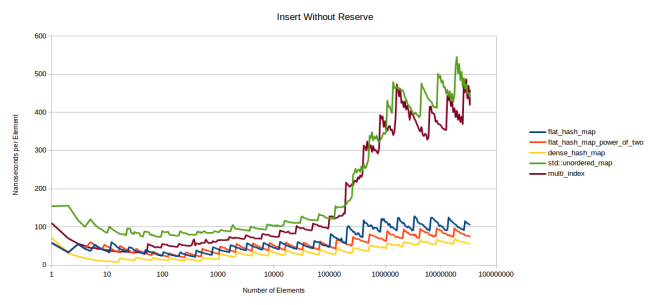
Зубцы ярко выражены, но направлены в другую сторону. Средняя стоимость подскакивает каждый раз, когда нужно перераспределить таблицу. Затем она снижается, пока снова не приходит время перераспределять.
Опять же, в левой части графика отражена ситуация, когда таблицы целиком умещаются в кеш L3. В этот раз я решил не писать текст с инициализацией промаха кеша, потому что это требует времени, да к тому же мы уже знаем, что правая часть графика — хорошая аппроксимация для промаха.
В этом бенчмарке google::dense_hash_map обошла мою новую таблицу, но не сильно. Дело в том, что dense_hash_map не перемещает элементы при вставке. Она просто ищет пустой слот и вставляет туда элемент. Используемое мной хеширование Robin Hood требует перемещать уже существующие элементы при вставке нового, чтобы сохранить свойство «каждый узел должен быть как можно ближе к своей идеальной позиции». Это компромисс между стоимостью вставки и скоростью поиска. Но я рад, что у меня небольшое падение производительности.
Теперь измерим, как будет вставляться элемент, если сначала вызвать reserve():
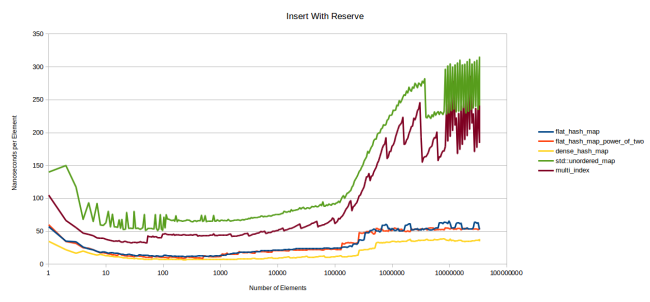
Не знаю, что происходит в конце с контейнерами на базе узлов. Интересно было бы разобраться, но я этого не сделал. Подозреваю, что дело в вызове malloc в моей стандартной библиотеке (Linux gcc). Во время измерений для этого и других графиков я столкнулся с несколькими проблемами, потому что некоторые операции по непонятным причинам занимали много времени.
Но в целом график выглядит аналогичным предыдущему, за исключением меньшей зубчатости из-за того, что reserve избавляет от необходимости перераспределять. Моя таблица выполняет вставку быстро, но не так, как google::dense_hash_map.
Теперь посмотрим, сколько времени уходит на удаление элементов. Для этого я построил массив из N элементов и замерил длительность удаления каждого из них в случайном порядке. Затем поделил общее время на N:
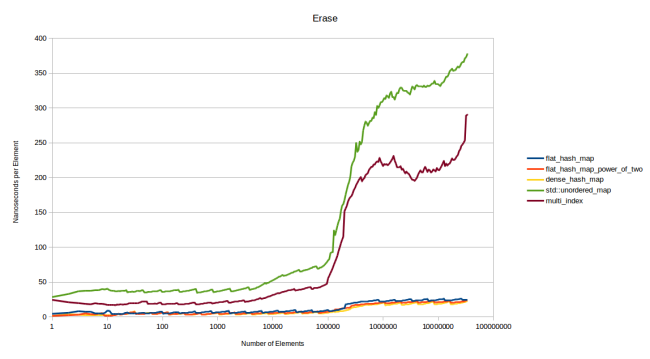
Контейнеры на базе узлов снова показали плохие результаты, остальные идут ноздря в ноздрю. Моя таблица стирает примерно за 23 наносекунды, а dense_hash_map — за 20. В целом обе работают очень быстро.
Но между ними есть одно большое различие: когда dense_hash_map стирает элемент, то оставляет в таблице «надгробие» (tombstone). Оно будет убрано только в том случае, если вы вставили в слот новый элемент. «Надгробие» представляет собой требование квадратичного размещения (quadratic probing), которое google::dense_hash_map выполняет в ходе поиска: при стирании элемента очень трудно найти другой элемент, чтобы взять его слот. При хешировании Robin Hood с его линейным размещением нет никаких трудностей с поиском элемента, который может занять опустевший слот: просто перемещаем следующий элемент вперёд, если он ещё не находится на своей идеальной позиции. А при квадратичных наборах может потребоваться элемент, расположенный через четыре слота. И при его перемещении снова придётся решать проблему поиска узла для вставки в свежеосвободившийся слот. Так что вместо этого вставляются «надгробия», которые игнорируются таблицей при поиске. Они будут заменены при следующей операции вставки.
Всё это означает, что если в таблице есть «надгробия», то она будет работать чуть медленнее. Поэтому быстрое удаление в dense_hash_map оборачивается некоторым замедлением поиска после удаления. Оценить это влияние довольно трудно, но мне кажется, что я нашёл подходящий тест: я снова и снова вставляю и удаляю элементы:
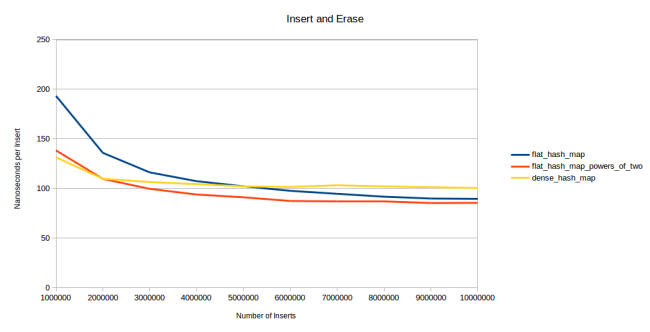
Сначала генерирую миллион случайных целых чисел. Затем вставляю их в хеш-таблицу, стираю, снова вставляю. Причём делаю это в случайном порядке. Скажем, у меня есть только четыре числа: 1, 2, 3 и 4. Правильный порядок для «вставить, стереть, снова вставить» будет: вставить 1, вставить 3, стереть 1, вставить 2, вставить 4, стереть 4, вставить 4, вставить 1, стереть 2, стереть 3, вставить 3, вставить 2. Каждый элемент вставляется, стирается и снова вставляется, но в случайном порядке. На графике показана длительность вставки одного элемента в зависимости от общего количества вставок. Первая контрольная точка — просто вставка миллиона элементов. Вторая — вставка миллиона элементов, их удаление и снова вставка (в случайном порядке). Третья контрольная точка — вставка, удаление, вставка, удаление, вставка. То есть всего три вставки. И так далее.
Поначалу dense_hash_map работает быстрее за счёт того, что у неё процедура вставки выполняется быстрее. На второй контрольной точке моя таблица её догнала, а на третьей — обогнала. После 6 миллионов вставок версия моей таблицы с простыми числами даже вышла на второе место. Мои таблицы становились всё быстрее, потому что чем больше удалений, тем ниже должен быть коэффициент заполнения. Если достаточно часто вставлять и удалять миллион элементов, то в таблице постоянно будет одномоментно находиться около 500 тыс. элементов. И чем дольше прогонять цикл вставка-удаление-вставка, тем ниже будет средняя одномоментная заполненность. Моя таблица от этого выигрывает, а в dense_hash_map накапливаются «надгробия», мешающие увеличивать производительность. Хотя по сравнению с другими таблицами dense_hash_map остаётся очень быстрой:
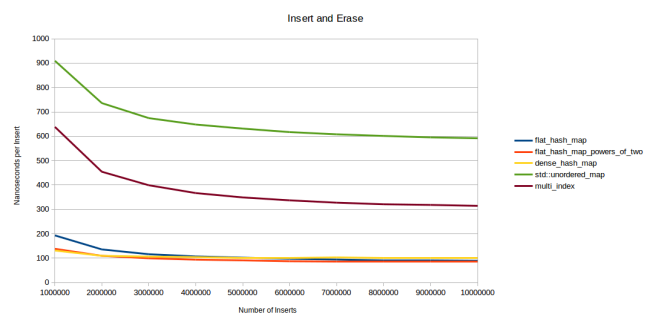
Как показывает график, использование квадратичного размещения в dense_hash_map полностью оправданно, даже с учётом вставки «надгробий». Эта таблица работает гораздо быстрее любых других контейнеров на базе узлов. Но всё же линейное размещение Robin Hood обеспечивает более элегантный способ удаления элементов: не составляет труда найти элемент, который отправится в освободившийся слот. Это будет преимуществом для страниц, где часто приходится удалять и вставлять элементы.
Сравнение таблиц с разным max_load_factor()
Давайте посмотрим, как можно решить проблему использования таблицами std::unordered_map и boost::multi_index коэффициента max_load_factor, равного 1,0, в то время как моя таблица и google::dense_hash_map используют 0,5. Станут ли другие таблицы работать быстрее при более низком max_load_factor? Чтобы выяснить это, я прибегнул к первому бенчмарку (удачный поиск), задал на каждой таблице max_load_factor 0,5. А затем провёл замеры перед самыми перераспределениями таблиц.
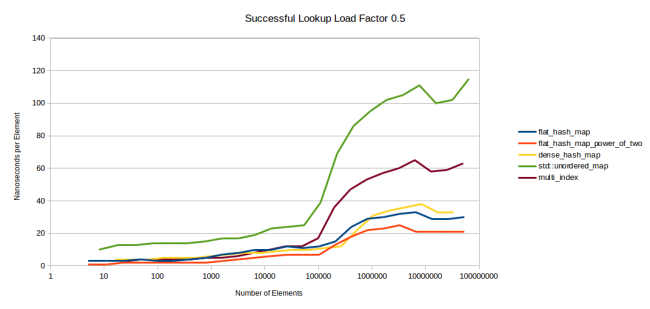
Итак, max_load_factor у всех равен 0,5, и я хотел измерить скорость работы, когда у них действительно будет такой коэффициент заполнения, так что я провёл измерения прямо перед перераспределениями. Если вернётесь к самому первому графику, то представьте, что я просто соединил прямыми линиями пики зубцов. Думаю, это правильный график, если вам нужно сравнить производительность хеш-таблиц напрямую, без влияния различных значений max_load_factor и стратегий перераспределения.
Здесь flat_hash_map работает быстрее dense_hash_map, как и в первом бенчмарке. Кстати, причина недолгого преимущества dense_hash_map в том, что эта таблица использует меньше памяти: она ещё помещается в кеш L3, а flat_hash_map уже нет.
Но всё же главной задачей этого бенчмарка было сравнение boost::multi_index и std::unordered_map, использующих max_load_factor 1,0, с flat_hash_map и dense_hash_map, чей max_load_factor — 0,5. Как видите, при одинаковом значении flat-таблицы работают быстрее.
Результат ожидаемый, но я считаю, что его нужно было подтвердить экспериментально. По ощущениям, это наиболее честный тест производительности хеш-таблиц, потому что здесь они сконфигурированы одинаково и имеют одинаковый коэффициент заполнения. Я не придерживался этого принципа в других бенчмарках, потому что в реальных ситуациях вы вряд ли будете менять max_load_factor. И в тех же реальных ситуациях вы будете наблюдать зубчатый график производительности, как на первой иллюстрации, когда одинаковые таблицы работают по-разному в зависимости от количества коллизий. И коэффициент заполнения — лишь один из факторов. Также этот график скрывает одно из преимуществ моей таблицы: ограничение количества наборов приводит к более стабильной производительности.
Разные ключи и значения
До сих пор я измерял производительность при сопоставлении целочисленного ключа и целочисленного значения (map from int to int). Но при разных ключах или более крупных значениях результаты могут быть иными. Для начала — вот графики удачных и неудачных поисков при использовании в качестве ключей строковых значений:

Это версия графика для таблиц, которые помещаются в кеш. Так было проще. Как видите, использование строковых значений лишь незначительно приподняло графики. Это было ожидаемо, потому что основные затраты связаны с изменением хеш-функции и более дорогим сравнением. Взглянем на неудачные поиски:
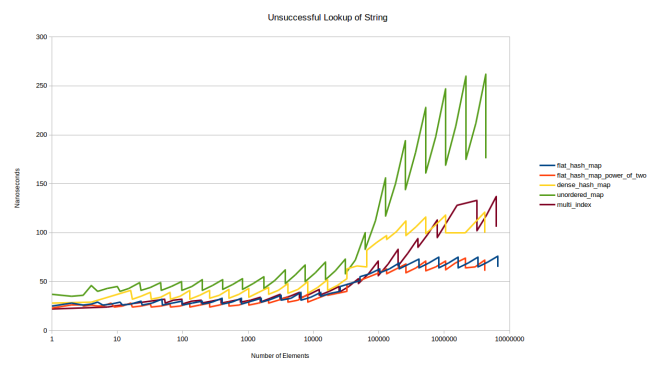
Очень интересно: похоже, поиск отсутствующего в таблице элемента в google::dense_hash_map обходится дороже, чем в boost::multi_index. Причина в следующем: при создании dense_hash_map вы должны предоставить специальный ключ, обозначающий пустой слот, и ещё один специальный ключ, обозначающий слот с «надгробием». Я использовал, соответственно, std::string(1, 0) и std::string(1, 255). Но это означает, что таблица должна сравнить строковые значения, чтобы увидеть, что слот пуст. Все остальные таблицы для этого сравнивают целочисленные значения.
Тем не менее если нам нужно сравнить лишь одиночные символы, то сравнение строковых значений остаётся недорогим. И действительно, накладные расходы не так уж велики. Они только выглядят такими на предыдущем графике, потому что при каждом поиске у нас было попадание в кеш. А вот при промахах кеша ситуация иная:
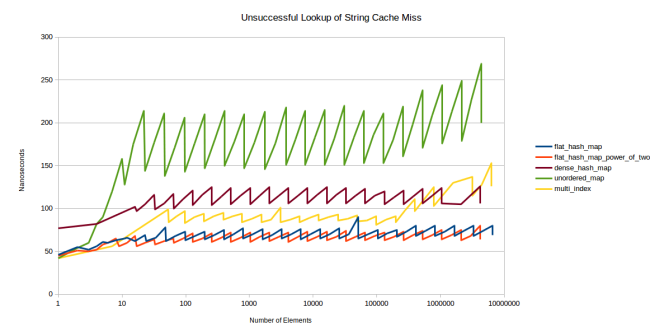
Здесь таблица уже не в кеше, dense_hash_map остаётся быстрее и уступает лишь на таблицах очень большого размера (больше миллиона записей). Я не выяснял причину.
Затем я поиграл с размером значения. А если у меня сопоставлены не целочисленные ключ и значение (map from int to int), а целочисленный ключ и 32-байтная структура? Или целочисленный ключ и 1024-байтная структура? Для операций поиска я построил 12 графиков ([целочисленное, 32-байтное, 1024-байтное] × [целочисленное, строковое] × [удачный поиск, неудачный поиск]), и большинство из них выглядели точно так же, как и вышеприведённые: все поиски строковых значений не зависели от размера значения, а большинство поисков целочисленных значений выглядели одинаково. За исключением одного: неудачного поиска целочисленного ключа и 1024-байтного значения:
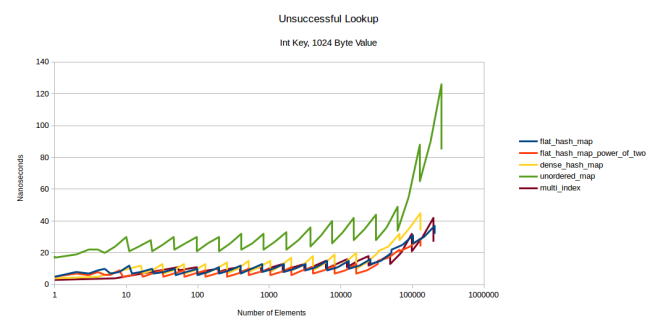
Как видите, при 1024-байтном значении multi_index может конкурировать с flat-таблицами. Причина в том, что при неудачном поиске приходится выполнять максимальное количество поисков, а при таком огромном типе-значении ваш prefetcher должен работать очень напряжённо. Моя таблица ещё удерживается в лидерах, но при 1024 байтах превращается в контейнер на базе узлов.
Графики для всех остальных поисков выглядят одинаково, потому что в случае с контейнерами на базе узлов вам не нужно беспокоиться о размере значения: всё распределено по отдельным кучам. В случае с flat-контейнерами можно ожидать увеличения количества промахов кеша. Но поскольку у нас max_load_factor равен 0,5, элемент довольно быстро обнаруживается в таблице. Чаще всего выполняется только один поиск: с помощью первого набора вы либо находите его, либо понимаете, что элемент в таблице отсутствует. Два обхода набора тоже бывают довольно часто, но три — уже редко. В моей таблице поиск выполняется линейно, потому что при линейном поиске процессоры прекрасно делают предварительную выборку (prefetch) следующего элемента вне зависимости от его размера.
Так что процедуры поиска по большей части не зависят от размера типа (size of the type), хотя графики вставок и удалений сильно отличаются. Вот график вставки с использованием целочисленного ключа и 32-байтной структуры в качестве значения:
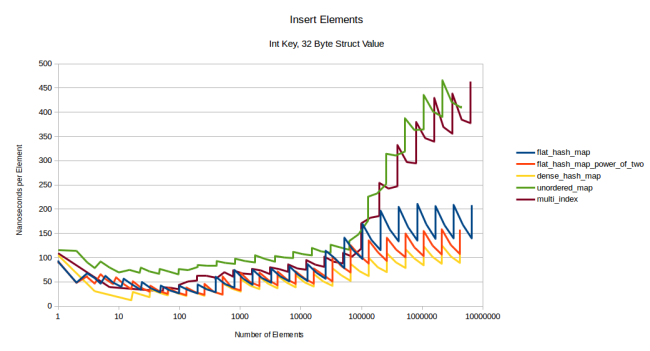
Все линии немного поднялись, но больше всего это проявилось у flat-таблиц, зубчатость у них тоже стала ярко выраженной: чем больше данных нужно перемещать, тем сильнее перераспределения ухудшают производительность. Но на контейнеры на базе узлов это не влияет, и boost::multi_index долгое время остаётся конкурентной. Давайте посмотрим, какая будет ситуация с 1024-байтной структурой:
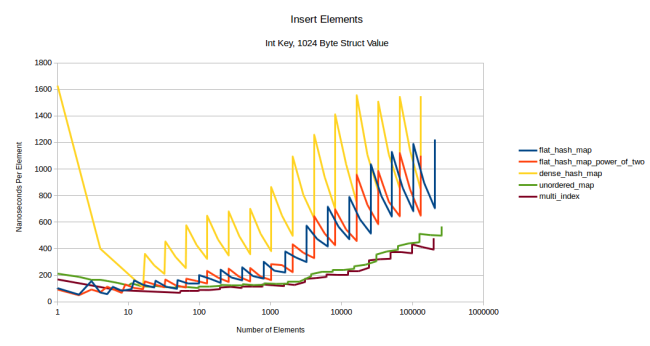
Всё изменилось: flat-контейнеры стали дороже, их графики имеют сильную зубчатость, а контейнеры на базе узлов сохранили свою производительность. В данном случае главную роль играет стоимость перераспределения.
Тут есть одна странность: в dense_hash_map очень дорого вставлять одиночный элемент (левая часть жёлтой линии). Причина в том, что эта таблица сначала распределяет 32 слота и заполняет их сконструированным по умолчанию типом-значением (default constructed value type). А поскольку размер моего типа-значения — 1024 байта, то таблице приходится обнулять 32 килобайта данных. Вероятно, на вас это не повлияет, но я должен был объяснить странность графика.
Также в этом бенчмарке dense_hash_map оказалась медленнее моей таблицы. Я не разбирался с причиной, но предположу, что всё дело опять в заполнении каждого слота сконструированным по умолчанию типом-значением, так что перераспределение получается ещё дороже из-за необходимости инициализации слотов, даже тех, что никогда не будут использоваться.
Если перераспределение дорого, то, чтобы его не делать, можно заранее вызывать применительно к контейнеру функцию reserve(). Посмотрим, что будет, когда мы вставим те же элементы, но с предварительным вызовом reserve():
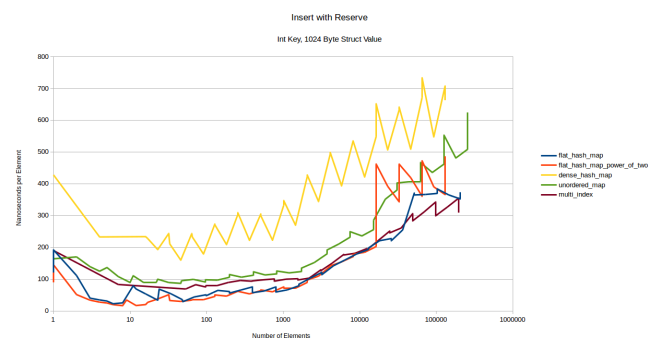
Сначала мой контейнер работает быстрее контейнеров на базе узлов, но в какой-то момент boost::multi_index обгоняет его. dense_hash_map по прежнему отстаёт, и причина, как мне кажется, по-прежнему в инициализации избыточного количества элементов и настолько большом значении, что даже инициализация всей таблицы с «пустой» парой ключ/значение занимает много времени. Вероятно, это можно оптимизировать, инициализируя для «пустой» пары только ключ без значения, но как часто вам приходится вставлять значение размером 1024 байта? В бенчмарке можно потестировать поведение контейнеров при вставке таких больших значений, но в реальной жизни вы можете никогда с этим не столкнуться.
Мои контейнеры остаются быстрее, пока не увеличиваются в размерах: при 16 385 элементах происходит внезапный скачок стоимости. С 16 384 элементами всё ещё работает быстро. Поскольку каждый элемент имеет размер 1028 байтов, то, когда контейнер становится больше 16 Мб, его скорость резко падает. Сначала я думал, что причина в случайном перераспределении из-за достижения ограничения по количеству наборов. Это было бы досадно, потому что выше я рассказывал о том, что вероятность такого события очень невелика. Но, к счастью, причина оказалась в другом: именно в этой контрольной точке резко возрастает количество времени, затрачиваемое на clear_page_c_e. Разобраться с этим мне помогла статья, в которой описывается стоимость обнуления памяти, в том числе применительно к функции clear_page_c_e. По какой-то причине именно в этой контрольной точке ОС начинает гораздо дольше предоставлять очищенные страницы памяти. Вас это может и не коснуться, в зависимости от диспетчера памяти и используемой ОС.
Хотя это также означает, что речь идёт о единовременном росте стоимости. После увеличения контейнера вы уже не столкнётесь с этим пиком на графике. Если контейнер живёт долго, всплеск стоимости будет сглажен.
Измерим теперь скорость вставки строковых ключей:
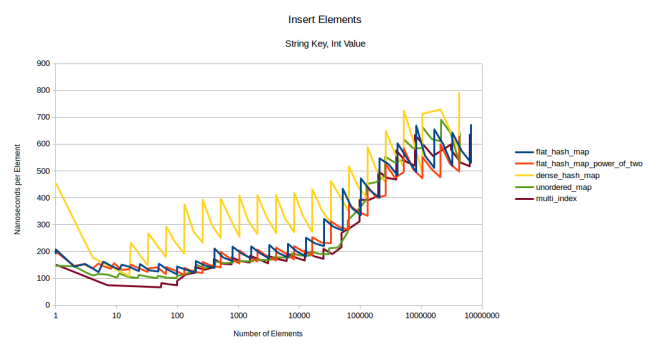
dense_hash_map оказалась на удивление медленной. Дело в том, что использованная мной версия этой таблицы (поставляется с Ubuntu 16.04) ещё не поддерживала семантику перемещения, поэтому копировать строковые не было нужды.
На этом графике мы будем по большей части сравнивать мою таблицу с контейнерами на базе узлов, и результат окажется не в пользу моей таблицы. Я снова виню более высокую стоимость перераспределения. Давайте попробуем сначала запускать reserve():
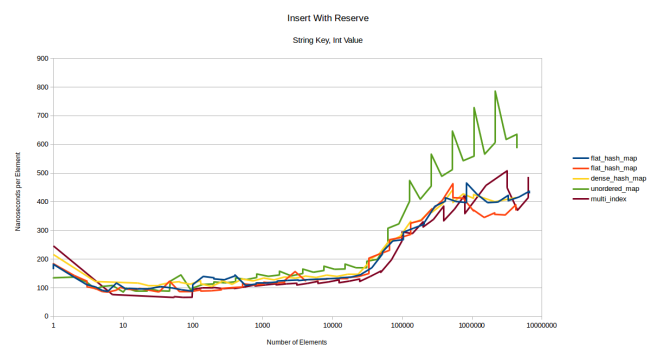
Честно говоря, я не знаю, какие тут можно сделать выводы. Здесь преобладает стоимость копирования строкового ключа, и все таблицы ведут себя схоже. Основной вывод: если ваш тип дорог в копировании, то это будет играть основную роль при вставке, так что лучше выбирать хеш-таблицу на основе других бенчмарков, например скорости поиска. При использовании строкового ключа с большим типом-значением мы будем наблюдать ту же картину:

dense_hash_map опять тормозит из-за инициализирования всех этих байтов. Другие таблицы идут кучно в связи с ключевой ролью стоимости копирования. Кроме того, моя таблица flat_hash_map_power_of_two имеет тот же самый странный всплеск при 16 385 элементах из-за роста продолжительности работы с clear_page_c_e.
Выводы: если у вас тип-значение большого размера, то все таблицы покажут низкую производительность вставки, поэтому лучше предварительно вызывать reserve(). Контейнеры на базе узлов оказываются гораздо более конкурентными решениями при использовании больших типов, чем маленьких.
Теперь измерим скорость удаления элементов. Я прогнал три теста для целочисленных ключей и три теста для строковых ключей: со значениями размером 4, 32 и 1024 байта. Выше был представлен график для 4-байтного значения. На 32 байтах результаты те же, так что я этот график не привожу. А с 1024 байтами ситуация такая:
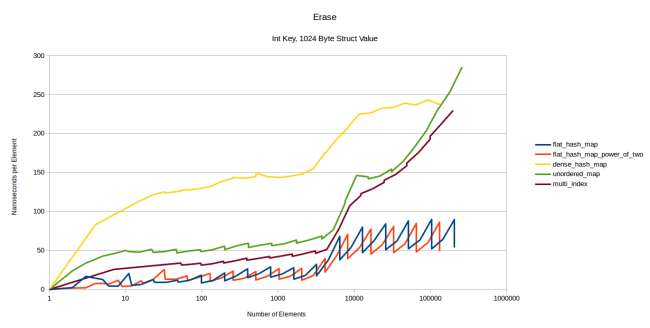
dense_hash_map работает гораздо медленнее. Проблема всё та же: другие таблицы просто считают элемент удалённым и вызывают деструктор, который является no-op для моей структуры, а dense_hash_map перезаписывает значение «пустой» парой ключ/значение, что представляет собой большую операцию, когда у вас 1024 байта данных.
Другое важное отличие: график удаления из flat_hash_map стал гораздо более зубчатым по сравнению с ранее измеренным удалением. При этом его линия существенно поднялась, то есть на этой операции таблица оказалась почти такой же медленной, как и контейнеры на базе узлов. Думаю, дело в том, что во время удаления элемента flat_hash_map приходится перемещать соседние элементы, а это дорогая операция, если у вас 1028 байтов данных.
Графики удаления строковых ключей выглядят достаточно похожими на графики удаления целочисленных, так что нет смысла их показывать. Вот один из них:
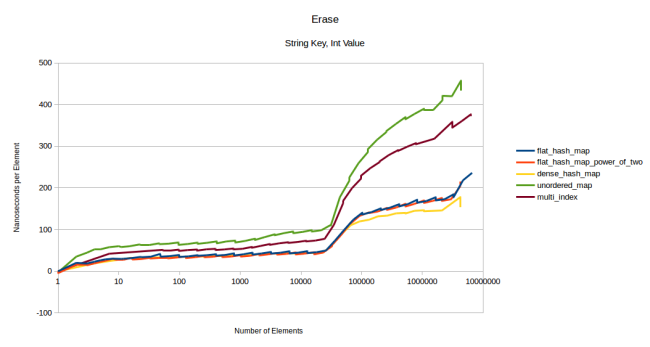
Если сделать размер значения 1024 байта, то график будет очень похож на один из вышеприведённых.
Последний тест — «вставка, удаление, снова вставка» в случайном порядке. Количество элементов я уменьшил до 10 тыс., потому что при 10 млн у меня на машине кончалась память. К тому же при 10 тыс. гораздо быстрее строятся графики. Начнём с типа-значения размером 32 байта:
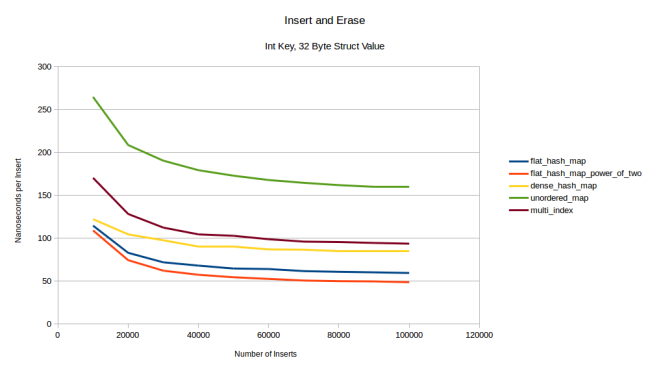
flat_hash_map обогнала dense_hash_map. Причём с ростом размера значения разрыв между ними увеличивается.
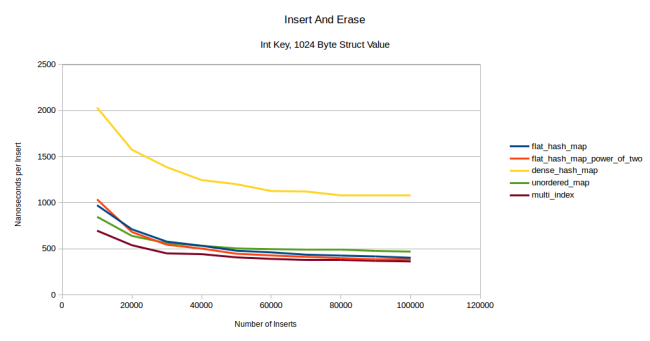
При большом размере типа-значения моя таблица обогнала dense_hash_map. Вначале она проигрывает контейнерам на базе узлов, но со временем нагоняет их. Причина в том, что я не вызывал предварительно функцию reserve(), поэтому при первой вставке таблица была вынуждена несколько раз перераспределиться. Для flat-контейнеров это очень дорого, а для контейнеров на базе узлов — дешевле. Но по мере стирания и вставки элементов стоимость перераспределения снижается, мои таблицы обгоняют unordered_map и в какой-то момент, вероятно, смогут обогнать multi_index. Если применить предварительное резервирование, то multi_index сразу оказывается позади:
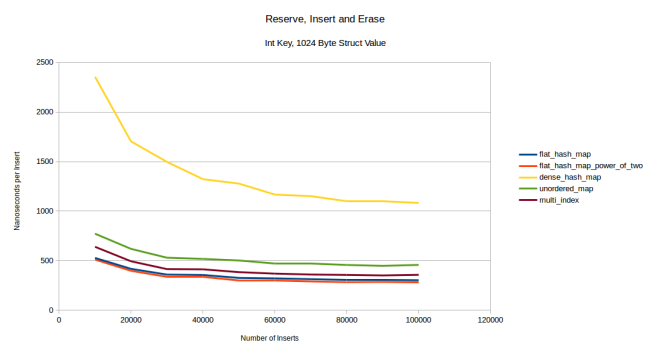
На самом деле я такого не ожидал, ведь даже с учётом резервирования моему контейнеру приходится перемещать больше элементов, что для 1028 байтов данных должно быть очень недёшево. Так что у меня есть лишь одно объяснение, почему мой контейнер оказался быстрее: у него достаточно низкий коэффициент заполнения и редко возникают коллизии. При прогоне этого теста со строковыми ключами я вижу, что мой контейнер предсказуемо замедляется, а на второе место выходит multi_index:
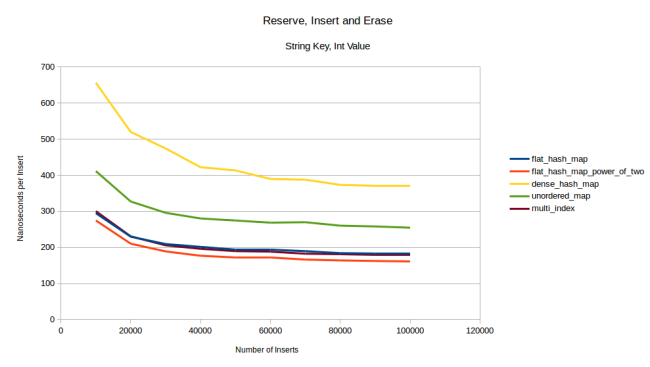
Другие графики вставки строковых ключей выглядят очень похоже на предыдущий. С 32-байтным типом-значением получается один в один. А если взять тип-значение размером 1024 байта, то графики получатся аналогичными тем, где ключ был целочисленным, как с резервированием, так и без.
Итоги по производительности
Проведя немало измерений, могу сказать, что тестировать хеш-таблицы на удивление сложно. Я не уверен, надо ли было тестировать все таблицы с одинаковым коэффициентом заполнения или с настройками по умолчанию. Я выбрал второй вариант. К тому же пришлось тестировать в разных условиях: с разными ключами, разными размерами значений и таблиц, с резервированием и без, и так далее. Тестов тоже пришлось сделать немало. Я мог бы вывалить в эту статью тысячи графиков, но это лишнее, так что подытожу:
- Моя новая таблица выполняет поиск быстрее всех остальных таблиц, которые я смог найти.
- Также она очень быстро выполняет вставки и удаления. Особенно если воспользоваться предварительным резервированием.
- Контейнеры на базе узлов могут быть быстрее при работе с большими типами, если вы не знаете заранее, сколько элементов у вас будет. Стоимость перераспределения губит производительность flat-контейнеров. Без перераспределений мой flat-контейнер оказывается самым быстрым во всех бенчмарках с использованием больших типов.
- Ключевым фактором при вставке строковых ключей является стоимость хеширования строковых значений, сравнения и копирования. Поэтому выбор хеш-таблицы не играет особой роли.
google::dense_hash_mapв ряде случаев демонстрировала неожиданное падение производительности.boost::multi_index— очень впечатляющая хеш-таблица. У неё очень высокая производительность для контейнера на базе узлов.- Если вы знаете, что ваша хеш-функция возвращает хорошее распределение значений, то вы можете значительно увеличить скорость работы, воспользовавшись моей хеш-таблицей, в которой размер массива определяется степенью двойки.
Исключения
При использовании моей таблицы можете без опаски бросать исключения в свой конструктор, в конструктор копий, в хеш-функцию, в функцию проверки равенства (equality function) и в аллокатор. Нельзя бросать исключения в конструктор перемещений (move constructor) или в деструктор. Дело в том, что моя таблица должна перемещать элементы и поддерживать инварианты. Но она не сможет этого делать, если вы будете бросать исключения в конструктор перемещений.
Исходный код и использование
Можете скачать исходный код с Github. Он распространяется под Boost-лицензией. Под общим заголовком вы найдёте ska::flat_hash_map и ska::flat_hash_set. Интерфейс такой же, как в std::unordered_map и std::unordered_set.
Есть одна сложность с использованием версии таблицы, в которой размер массива определяется степенью двойки. Я выше это объяснял, ищите по ska::power_of_two_hash_policy.
Также хочу обратить ваше внимание, что max_load_factor у меня по умолчанию равен 0,5. Можете спокойно задавать ему значения вплоть до 0,9. Только имейте в виду, что есть вероятность перераспределения таблицы до достижения этого ограничения. Она склонна к перераспределению до того, как заполнится на 70 %, потому что упирается в ограничение максимального количества наборов. Но если вас не смущает возможность неожиданного перераспределения, то можете сэкономить память и назначить max_load_factor значение повыше, это приведёт к незначительному падению производительности.
Итог
Думаю, я написал самую быструю хеш-таблицу. Она определённо быстрее всех выполняет поиск и очень быстро выполняет вставки и удаления. Главное — задайте ограничение максимального количества наборов. Его можно вычислить как log2(n), что в худшем случае даст временную сложность операции поиска на уровне O(log(n)) вместо O(n). Это большая разница. Ограничение количества наборов прекрасно сочетается с хешированием Robin Hood и позволяет выполнять ряд тонких оптимизаций внутреннего цикла.
Хеш-таблица распространяется под Boost-лицензией в виде версий hash_map и hash_set. Приятного использования!
