
(Полный исходный код лежит тут)
Сидя на пятичасовом занятии по химии, я часто скользил взглядом по таблице Менделеева, висящей на стене. Чтобы скоротать время, я начал искать слова, которые мог бы написать, используя лишь обозначения элементов из таблицы. Например: ScAlEs, FeArS, ErAsURe, WAsTe, PoInTlEsSnEsS, MoISTeN, SAlMoN, PuFFInEsS.
Затем я подумал, какое самое длинное слово можно составить (мне удалось подобрать TiNTiNNaBULaTiONS), поэтому я решил написать программу на Python, которая искала бы слова, состоящие из обозначений химических элементов. Она должна была получать слово и возвращать все его возможные варианты преобразования в наборы химических элементов:
Генерирование группировок обозначений
Если бы обозначения всех элементов были одной длины, задача оказалась бы тривиальной. Но некоторые обозначения состоят из двух символов, некоторые — из одного. Это сильно усложняет дело. Например, pu в Amputations может означать плутоний (Pu) или фосфор с ураном (PU). Любое входное слово нужно разбивать на все возможные комбинации одно- и двухсимвольных обозначений.
Такие преобразования я решил назвать «группировки». Они определяют конкретное разделение слова на обозначения. Группировка может быть представлена как кортеж из единиц и двоек, где 1 представляет односимвольное обозначение, а 2 — двухсимвольное. Каждое разбиение на элементы соответствует какой-то группировке:
- 'AmPuTaTiONS'
(2,2,2,2,1,1,1)
- 'AmPUTaTiONS'
(2,1,1,2,2,1,1,1)
Анализируя задачу, в попытке найти паттерны я написал в тетради такую таблицу.
Вопрос: дана строка длиной n, сколько для неё может существовать последовательностей единиц и двоек, чтобы количество цифр в каждой последовательности равнялось n?
| n | # группировок | Группировки |
|---|---|---|
| 0 | 1 | () |
| 1 | 1 | (1) |
| 2 | 2 | (1,1), (2) |
| 3 | 3 | (1,1,1), (2,1), (1,2) |
| 4 | 5 | (1,1,1,1), (2,1,1), (1,2,1), (1,1,2), (2,2) |
| 5 | 8 | (1,1,1,1,1), (2,1,1,1), (1,2,1,1), (1,1,2,1), (1,1,1,2), (2,2,1), (2,1,2), (1,2,2) |
| 6 | 13 | (1,1,1,1,1,1), (2,1,1,1,1), (1,2,1,1,1), (1,1,2,1,1), (1,1,1,2,1), (1,1,1,1,2), (2,2,1,1), (2,1,2,1), (2,1,1,2), (1,2,2,1), (1,2,1,2), (1,1,2,2), (2,2,2) |
| 7 | 21 | (1,1,1,1,1,1,1), (2,1,1,1,1,1), (1,2,1,1,1,1), (1,1,2,1,1,1), (1,1,1,2,1,1), (1,1,1,1,2,1), (1,1,1,1,1,2), (2,2,1,1,1), (2,1,2,1,1), (2,1,1,2,1), (2,1,1,1,2), (1,2,2,1,1), (1,2,1,2,1), (1,2,1,1,2), (1,1,2,2,1), (1,1,2,1,2), (1,1,1,2,2), (2,2,2,1), (2,2,1,2), (2,1,2,2), (1,2,2,2) |
Ответ: fib(n + 1)!?
Я был удивлён, обнаружив последовательность Фибоначчи в таком неожиданном месте. Во время последующих изысканий я был удивлён ещё больше, узнав, что об этом паттерне было известно ещё две тысячи лет назад. Стихотворцы-просодисты из древней Индии открыли его, исследуя преобразования коротких и длинных слогов ведических песнопений. Об этом и о других прекрасных исследованиях в истории комбинаторики можете почитать в главе 7.2.1.7 книги The Art of Computer Programming Дональда Кнута.
Я был впечатлён этим открытием, но всё ещё не достиг начальной цели: генерирования самих группировок. После некоторых размышлений и экспериментов я пришёл к наиболее простому решению, какое смог придумать: сгенерировать все возможные последовательности единиц и двоек, а затем отфильтровать те, сумма элементов которых не совпадает с длиной входного слова.
from itertools import chain, product
def generate_groupings(word_length, glyph_sizes=(1, 2)):
cartesian_products = (
product(glyph_sizes, repeat=r)
for r in range(1, word_length + 1)
)
# включаем группировки, состоящие только из правильного количества символов
groupings = tuple(
grouping
for grouping in chain.from_iterable(cartesian_products)
if sum(grouping) == word_length
)
return groupingsДекартово произведение — это набор всех кортежей, скомпонованных из имеющегося набора элементов. Стандартная библиотека Python предоставляет функцию itertools.product(), которая возвращает декартово произведение элементов для данного итерируемого. cartesian_products — генерирующее выражение, которое собирает все возможные преобразования элементов в glyph_sizes вплоть до заданной в word_length длины.
Если word_length равно 3, то cartesian_products сгенерирует:
[
(1,), (2,), (1, 1), (1, 2), (2, 1), (2, 2), (1, 1, 1), (1, 1, 2),
(1, 2, 1), (1, 2, 2), (2, 1, 1), (2, 1, 2), (2, 2, 1), (2, 2, 2)
]Затем результат фильтруется, чтобы groupings включало только те преобразования, количество элементов которых удовлетворяет word_length.
>>> generate_groupings(3)
((1, 2), (2, 1), (1, 1, 1))Конечно, здесь много лишней работы. Функция вычислила 14 преобразований, но остались только 3. Производительность сильно падает с увеличением длины слова. Но к этому мы вернёмся позже. А пока я получил работающую функцию и перешёл к следующей задаче.
Сопоставление слов с группировками
После вычисления всех возможных группировок для слова нужно было «сопоставить» его с каждой из группировок:
def map_word(word, grouping):
chars = (c for c in word)
mapped = []
for glyph_size in grouping:
glyph = ""
for _ in range(glyph_size):
glyph += next(chars)
mapped.append(glyph)
return tuple(mapped)Функция обращается с каждым обозначением в группировке, как с чашкой: сначала заполняет её таким количеством символов из слова, каким сможет, а затем переходит к следующему. Когда все символы будут помещены в правильные обозначения, получившееся сопоставленное слово возвращается в виде кортежа:
>>> map_word('because', (1, 2, 1, 1, 2))
('b', 'ec', 'a', 'u', 'se')После сопоставления слово готово к сравнению со списком обозначений химических элементов.
Поиск вариантов написания
Я написал функцию spell(), которая собирает вместе все предыдущие операции:
def spell(word, symbols=ELEMENTS):
groupings = generate_groupings(len(word))
spellings = [map_word(word, grouping) for grouping in groupings]
elemental_spellings = [
tuple(token.capitalize() for token in spelling)
for spelling in spellings
if set(s.lower() for s in spelling) <= set(s.lower() for s in symbols)
]
return elemental_spellingsspell() получает все возможные варианты написания и возвращает только те из них, которые полностью состоят из обозначений элементов. Для эффективной фильтрации неподходящих вариантов я использовал множества (set).
Множества в Python очень похожи на математические множества. Это неупорядоченные коллекции уникальных элементов. За кулисами они реализованы как словари (хеш-таблицы) с ключами, но без значений. Поскольку все элементы множества хешируемы, то проверка на принадлежность (membership test) работает очень эффективно (в среднем О(1)). Операторы сравнения перегружаются для проверки на подмножества с использованием этих эффективных операций по проверке на принадлежность. Множества и словари хорошо описаны в замечательной книге Fluent Python Лучано Рамальо (Luciano Ramalho).
Заработал последний компонент, и я получил функционирующую программу!
>>> spell('amputation')
[('Am', 'Pu', 'Ta', 'Ti', 'O', 'N'), ('Am', 'P', 'U', 'Ta', 'Ti', 'O', 'N')]
>>> spell('cryptographer')
[('Cr', 'Y', 'Pt', 'Og', 'Ra', 'P', 'H', 'Er')]Самое длинное слово?
Довольный своей реализацией основной функциональности, я назвал программу Stoichiograph и сделал для неё обёртку, использующую командную строку. Обёртка берёт слово в качестве аргумента или из файла и выводит варианты написания. Добавив функцию сортировки слов по убыванию, я натравил программу на список слов.
$ ./stoichiograph.py --sort --batch-file /usr/share/dict/american-english
NoNRePReSeNTaTiONaL
NoNRePReSeNTaTiONAl
[...]Отлично! Сам я бы это слово не нашёл. Программа уже решает поставленную задачу. Я поигрался ещё и нашёл более длинное слово:
$ ./stoichiograph.py nonrepresentationalisms
NoNRePReSeNTaTiONaLiSmS
NONRePReSeNTaTiONaLiSmS
NoNRePReSeNTaTiONAlISmS
NONRePReSeNTaTiONAlISmSИнтересно. Мне захотелось узнать, действительно ли это самое длинное слово (спойлер), и я решил исследовать более длинные слова. Но сначала нужно было разобраться с производительностью.
Решение проблем с производительностью
Обработка 119 095 слов (многие из которых были довольно короткими) заняла у программы примерно 16 минут:
$ time ./stoichiograph.py --sort --batch-file /usr/share/dict/american-english
[...]
real 16m0.458s
user 15m33.680s
sys 0m23.173sВ среднем около 120 слов в секунду. Я был уверен, что можно делать гораздо быстрее. Мне требовалась более подробная информация о производительности, чтобы понять, где копать.
Line profiler — инструмент для определения узких мест в производительности кода на Python. Я воспользовался им для профилирования программы, когда она искала написание для 23-буквенного слова. Вот сжатая версия отчёта:
Line # % Time Line Contents
===============================
30 @profile
31 def spell(word, symbols=ELEMENTS):
32 71.0 groupings = generate_groupings(len(word))
33
34 15.2 spellings = [map_word(word, grouping) for grouping in groupings]
35
36 elemental_spellings = [
37 0.0 tuple(token.capitalize() for token in spelling)
38 13.8 for spelling in spellings
39 if set(s.lower() for s in spelling) <= set(s.lower() for s in symbols)
40 ]
41
42 0.0 return elemental_spellings
Line # % Time Line Contents
===============================
45 @profile
46 def generate_groupings(word_length, glyhp_sizes=(1, 2)):
47 cartesian_products = (
48 0.0 product(glyph_sizes, repeat=r)
49 0.0 for r in range(1, word_length + 1)
50 )
51
52 0.0 groupings = tuple(
53 0.0 grouping
54 100.0 for grouping in chain.from_iterable(cartesian_products)
55 if sum(grouping) == word_length
56 )
57
58 0.0 return groupingsНеудивительно, что generate_groupings() работает так долго. Проблема, которую она пытается решить, — это особый случай задачи о сумме подмножеств, которая является NP-полной задачей. Поиск декартова произведения быстро становится дорогим, а generate_groupings() ищет многочисленные декартовы произведения.
Можно провести асимптотический анализ, чтобы понять, насколько всё плохо:
- Мы предполагаем, что
glyph_sizesвсегда содержат два элемента (1 и 2). product()находитrраз декартово произведение множества из двух элементов, так что временная сложность дляproduct()равнаO(2^r).product()вызывается в цикле, который повторяетсяword_lengthраз, так что, если мы приравняемnкword_length, временная сложность для всего цикла будет равнаO(2^r * n).- Но
rполучает разные значения при каждом прогоне цикла, так что на самом деле временная сложность ближе кO(2^1 + 2^2 + 2^3 + ... + 2^(n-1) + 2^n). - А поскольку
2^0 + 2^1 + ... + 2^n = 2^(n+1) - 1, результирующая временная сложность равнаO(2^(n+1) - 1), илиO(2^n).
С O(2^n) можно ожидать, что время выполнения будет удваиваться при каждом инкрементировании word_length. Ужасно!
Я раздумывал над проблемой производительности много недель. Нужно было решить две взаимосвязанных, но различных задачи:
- Обработка списка слов разной длины.
- Обработка одного, но очень длинного слова.
Вторая задача оказалась гораздо важнее, потому что она влияла на первую. Хотя я сразу не придумал, как улучшить обработку во втором случае, но у меня были идеи насчёт первого, потому я с него и начал.
Задача 1: быть ленивым
Лень — добродетель не только для программистов, но и для самих программ. Решение первой задачи требовало добавления лени. Если программа будет проверять длинный список слов, то как сделать так, чтобы она выполняла как можно меньше работы?
Проверка на неправильные символы
Естественно, я подумал, что в списке наверняка есть слова, содержащие символы, не представленные в таблице Менделеева. Нет смысла тратить время на поиск написаний для таких слов. А значит, список можно будет обработать быстрее, если быстро найти и выкинуть такие слова.
К сожалению, единственными символами, не представленными в таблице, оказались j и q.
>>> set('abcdefghijklmnopqrstuvwxyz') - set(''.join(ELEMENTS).lower())
('j', 'q')А в моём словаре только 3 % слов содержали эти буквы:
>>> with open('/usr/share/dict/american-english', 'r') as f:
... words = f.readlines()
...
>>> total = len(words)
>>> invalid_char_words = len(
... [w for w in words if 'j' in w.lower() or 'q' in w.lower()]
... )
...
>>> invalid_char_words / total * 100
3.3762962340988287Выкинув их, я получил прирост производительности всего на 2 %:
$ time ./stoichiograph.py --sort --batch-file /usr/share/dict/american-english
[...]
real 15m44.246s
user 15m17.557s
sys 0m22.980sЭто было не то улучшение, на которое я надеялся, так что я перешёл к следующей идее.
Мемоизация
Мемоизация — это методика сохранения выходных данных функции и их возврата, если функция снова вызывается с теми же входными данными. Мемоизированной функции нужно на основании конкретных входных только один раз сгенерировать выходные данные. Это очень полезно при использовании дорогих функций, многократно вызываемых с одними и теми же несколькими входными данными. Но работает мемоизация только для чистых функций.
generate_groupings() была идеальным кандидатом. Она вряд ли столкнётся с очень большим диапазоном входных данных и очень дорога в выполнении при обработке длинных слов. Пакет functools облегчает мемоизацию, предоставляя декоратор @lru_cache().
Мемоизация generate_groupings() привела к тому, что время выполнения уменьшилось — заметно, хотя и недостаточно:
$ time ./stoichiograph.py --sort --batch-file /usr/share/dict/american-english
[...]
real 11m15.483s
user 10m54.553s
sys 0m17.083sНо всё же неплохо для единственного декоратора из стандартной библиотеки!
Задача 2: быть умным
Мои оптимизации немного помогли с первой задачей, но ключевой нерешённой проблемой оставалась неэффективность работы generate_groupings(), большие отдельные слова всё ещё обрабатывались очень долго:
$ time ./stoichiograph.py nonrepresentationalisms
[...]
real 0m20.275s
user 0m20.220s
sys 0m0.037sЛень может привести к определённому прогрессу, но иногда нужно быть умным.
Рекурсия и DAG
Задремав однажды вечером, я испытал вспышку вдохновения и побежал к маркерной доске, чтобы нарисовать это:

Я подумал, что могу взять любую строку, вытащить все одно- и двухсимвольные обозначения, а затем в обоих случаях рекурсировать оставшуюся часть. Пройдя по всей строке, я найду все обозначения элементов и, что особенно важно, получу информацию об их структуре и порядке расположения. Также я подумал, что граф может быть отличным вариантом для хранения такой информации.
Если серия рекурсивных вызовов функции для прекрасного слова amputation выглядит так:
'a' 'mputation'
'm' 'putation'
'p' 'utation'
'u' 'tation'
't' 'ation'
'a' 'tion'
't' 'ion'
'i' 'on'
'o' 'n'
'n' ''
'on' ''
'io' 'n'
'ti' 'on'
'at' 'ion'
'ta' 'tion'
'ut' 'ation'
'pu' 'tation'
'mp' 'utation'
'am' 'putation'то после фильтрации всех обозначений, не удовлетворяющих таблице Менделеева, можно получить подобный граф:
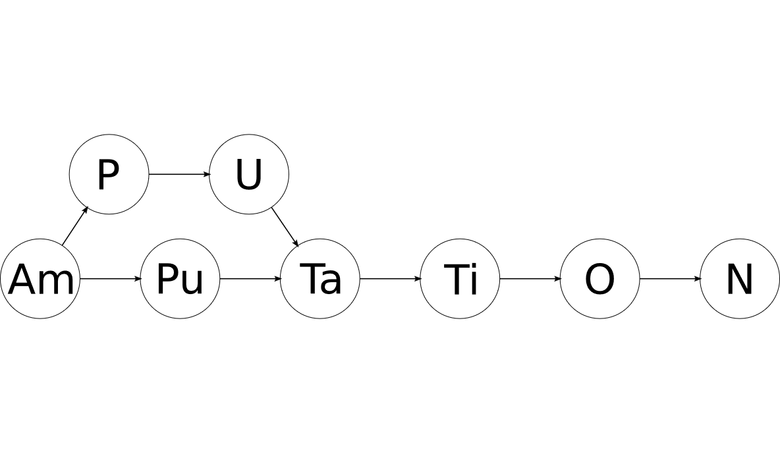
Получился направленный ациклический граф (DAG), каждый узел которого содержит обозначение химического элемента. Все пути от первого узла к последнему будут валидными написаниями исходного слова в виде химических элементов!
До этого я не работал с графами, но нашёл очень полезное эссе, в котором описаны основы, включая эффективный поиск всех путей между двумя узлами. В прекрасной книге 500 Lines or Less есть глава с другим примером реализации графа на Python. Эти примеры я и взял за основу.
Реализовав и протестировав простой графовый класс, я превратил свой рисунок на доске в функцию:
# Один узел графа. Обозначение химического элемента и его позиция в слове.
Node = namedtuple('Node', ['value', 'position'])
def build_spelling_graph(word, graph, symbols=ELEMENTS):
"""Даётся слово и граф, надо найти все одно- и двухсимвольные
обозначения элементов. Добавляем их в граф, только если они соответствуют
заданному множеству допустимых символов.
"""
def pop_root(remaining, position=0, previous_root=None):
if remaining == '':
graph.add_edge(previous_root, None)
return
single_root = Node(remaining[0], position)
if single_root.value.capitalize() in symbols:
graph.add_edge(previous_root, single_root)
if remaining not in processed:
pop_root(
remaining[1:], position + 1, previous_root=single_root
)
if len(remaining) >= 2:
double_root = Node(remaining[0:2], position)
if double_root.value.capitalize() in symbols:
graph.add_edge(previous_root, double_root)
if remaining not in processed:
pop_root(
remaining[2:], position + 2, previous_root=double_root
)
processed.add(remaining)
processed = set()
pop_root(word)Выигрыш
В то время как алгоритм «в лоб» выполнялся ужасно долго (O(2^n)), рекурсивный длился O(n). Гораздо лучше! Когда я в первый раз прогнал свежеоптимизированную программу на своём словаре, то был потрясён:
$ time ./stoichiograph.py --sort --batch-file /usr/share/dict/american-english
[...]
real 0m11.299s
user 0m11.020s
sys 0m0.17ysВместо 16 минут я получил 10 секунд, вместо 120 слов в секунду — 10 800 слов!
Впервые я действительно оценил силу и ценность структур данных и алгоритмов.
Самое длинное слово
С новоприобретёнными возможностями я смог отыскать самое длинное слово, разбиваемое на химические элементы: floccinaucinihilipilificatiousness. Это производное от floccinaucinihilipilification, что означает действие или привычку описывать что-то или относиться к чему-либо как к неважному, не имеющему ценности или бесполезному. Это слово часто называют самым длинным нетехническим словом в английском языке.
Floccinaucinihilipilificatiousness можно представить в виде 54 написаний, все они зашифрованы в этом прекрасном графе:
Хорошо потраченное время
Кто-то может сказать, что всё вышеописанное — полная ерунда, но для меня это стало ценным и важным опытом. Когда я начинал свой проект, то был относительно неопытен в программировании и не представлял, с чего начать. Дело двигалось медленно, и прошло немало времени, пока я добился удовлетворительного результата (см. историю коммитов, там видны большие перерывы, когда я переключался на другие проекты).
Тем не менее я многому научился и много с чем познакомился. Это:
- Комбинаторика
- Профилирование производительности
- Временная сложность
- Мемоизация
- Рекурсия
- Графы и деревья
Мне неоднократно помогало понимание этих концепций. Особенно оказались важны для моего проекта по симуляции n-тел рекурсии и деревья.
Наконец, приятно было отыскать ответ на собственный изначальный вопрос. Я знаю, что больше не нужно раздумывать над разбиением на химические элементы, потому что у меня теперь есть для этого инструмент, который можете получить и вы с помощью pip install stoichiograph.
Обсуждение
Добрые люди (и несколько благонамеренных ботов) поучаствовали в обсуждении этой статьи в ветке r/programming.
Допматериалы
Я получил немалую часть вдохновения из элегантных решений некоторых интересных проблем, решения принадлежат Питеру Норвигу (Peter Norvig):
Две информативные статьи о профилировании производительности в Python:

