Прошел месяц с появления моей первой статьи на Хабре и 20 дней с момента появления второй статьи про линейную регрессию. Статистика по просмотрам и целевым действиям аудитории копится, и именно она послужила отправной точкой для данной статьи. В ней мы коротко рассмотрим пример нелинейной регрессии (а именно, экспоненциальной) и с ее помощью построим модель конверсии, выделив среди пользователей две группы.
Когда известно, что случайная величина y зависит от чего-то (например, от времени или от другой случайной величины x) линейно, т.е. по закону y(x)= Ax+b, то применяется линейная регрессия (так в прошлой статье мы строили зависимость числа регистраций от числа просмотров). Для линейной регрессии коэффициенты A и b вычисляются по известным формулам. В случае регрессии другого вида, например, экспоненциальной, для того чтобы определить неизвестные параметры, необходимо решить соответствующую оптимизационную задачу: а именно, в рамках метода наименьших квадратов (МНК) задачу нахождения минимума суммы квадратов (y(xi) — yi)2.
Итак, вот данные, которые будем использовать в качестве примера. Пики посещаемости (ряд Views, красный пунктир) приходятся на моменты выхода статей. Второй ряд данных (Regs, с множителем 100) показывает число читателей, выполнивших после прочтения определенное действие (регистрацию и скачивание Mathcad Express – с его помощью, к слову, вы сможете повторить все расчеты этой и предыдущих статей). Все картинки — это скриншоты Mathcad Express, а файл с расчетами вы можете взять здесь.
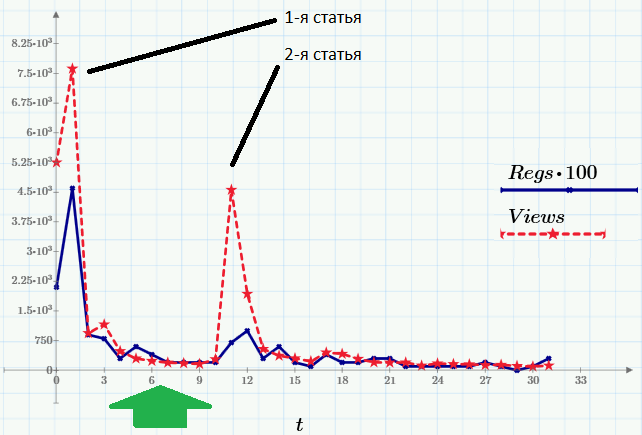
Зеленой стрелкой на графике я обозначил фрагмент данных, для которого мы будем строить нелинейную регрессию. Согласно модели, которую мы примем за основу, после короткого переходного периода после выхода публикации, количество просмотров уменьшается со временем приблизительно по экспоненциальному закону:
Views ≈ C0∙exp(C1∙t).
Обоснование этой модели пока отложим до одной из будущих статей, когда речь пойдет о пуассоновском случайном процессе.
Понятно, что для анализа нужно выбрать тот фрагмент, который соответствует модели (на слишком близко к начальному пику и без суммирования со статистикой посещений после выхода второй статьи). Именно этот промежуток выделен зеленой стрелкой на первом графике, а в более крупном масштабе он выглядит вот так:
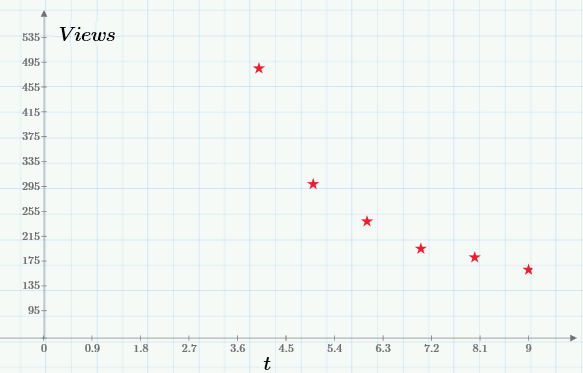
Экспоненциальная регрессия, напомню, определит график такой экспоненциальной функции, который будет «в среднем» ближе всего располагаться к показанным экспериментальным точкам. Для того чтобы найти коэффициенты регрессии, необходимо будет решить оптимизационную задачу на отыскание минимума целевой функции:
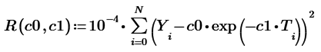
(T,Y) – массив из N экспериментальных точек, а множитель мы ввели для удобства (он не влияет на положение минимума). Дальше, конечно, можно было бы сразу написать одну-две строчки кода со встроенной функцией поиска минимума для получения искомых С0 и С1, однако, мы используем бесплатный Mathcad Express, где все они выключены, поэтому пойдем чуть более громоздким (зато более простым для понимания и наглядным) путем.
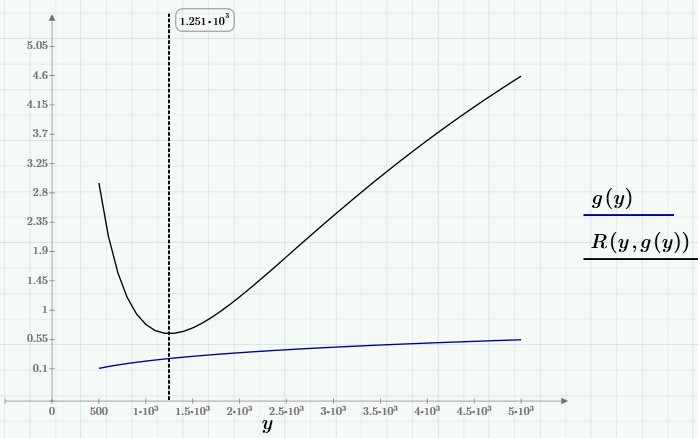
Для начала, посмотрим, как ведет себя функция R(c0, c1). Для этого зафиксируем несколько значений с0 и построим для каждого из них график функции одной переменной R(c0, х).
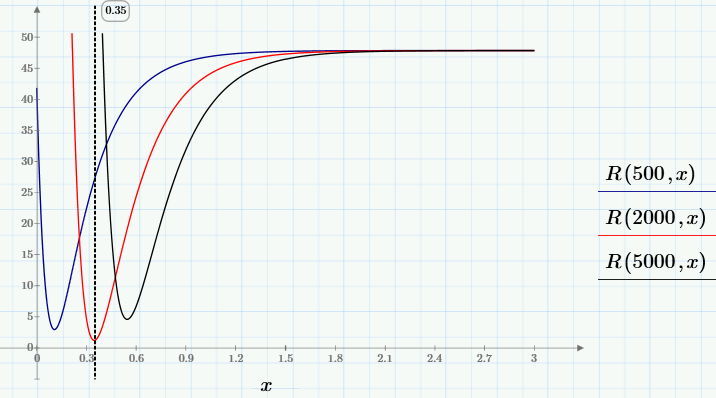
Видно, что для выбранных с0 любой из графиков семейства имеет один минимум, положение которого х зависит от с0, т.е. можно записать x=g(c0). Самый глубокий минимум, т.е., минимум R(c0, g(c0))~min будет искомым глобальным минимумом. Его-то нам и надо найти для решения задачи. Чтобы найти глобальный минимум, сначала (средствами, доступными в Mathcad Express) определим пользовательскую функцию g(y), а потом найдем минимум R(y, g(y)).
Не буду останавливаться на численном алгоритме вычисления минимума (кому интересно, он приведен в первой строчке следующего скриншота). Решение задачи (точка, в выбранных обозначениях с0=y0 и с1=х0), значение целевой функции в этой точке и график регрессии приведен ниже:
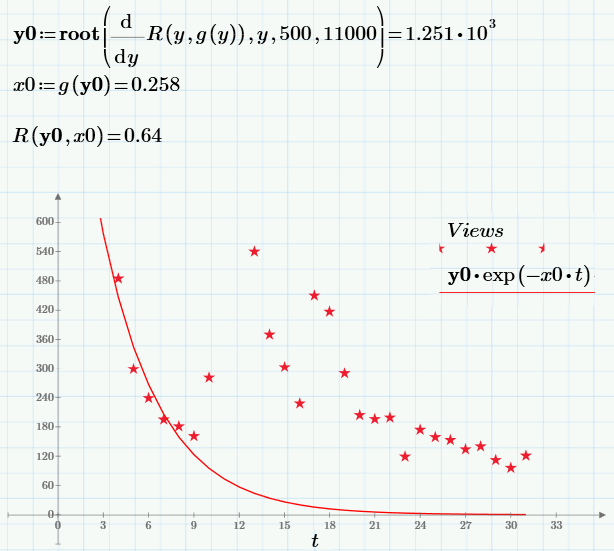
Может ли нас удовлетворить полученный результат? Скорее нет, поскольку построенная регрессия не очень хорошо ложится на экспериментальные точки. Мешает «хвост», который сильно отличается у регрессии (экспонента быстро падает почти до нуля) и данных (как видно, даже по прошествии значительного времени число просмотров ненулевое, а составляет значение около сотни).
Поэтому для улучшения результата давайте усовершенствуем модель. Будем считать моделью числа просмотров статьи сумму посещений, идущих по двум каналам:
Этот третий параметр с2 как раз можно определить из анализа «хвоста» данных, когда пуассоновских посетителей практически нет, просто как среднее значение просмотров за последние 10 дней наблюдений.
Наконец, зная с2, можно построить уточненную регрессию вида
Views ≈ с0∙exp(с1∙t)+с2,
полностью повторив описанный выше алгоритм:

Обратите внимание на то, что значение целевой функции в минимуме (т.е. сумма квадратов невязок) снижается по сравнению со случаем с2=0 больше, чем на порядок!
В заключение, приведу результат работы встроенной функции expfit для нахождения экспоненциальной регрессии (имеющейся в коммерческой версии Mathcad Prime). Результат работы показан на графике зеленым пунктиром, а наш результат (тот же, что и на предыдущем графике) – красной сплошной линией.
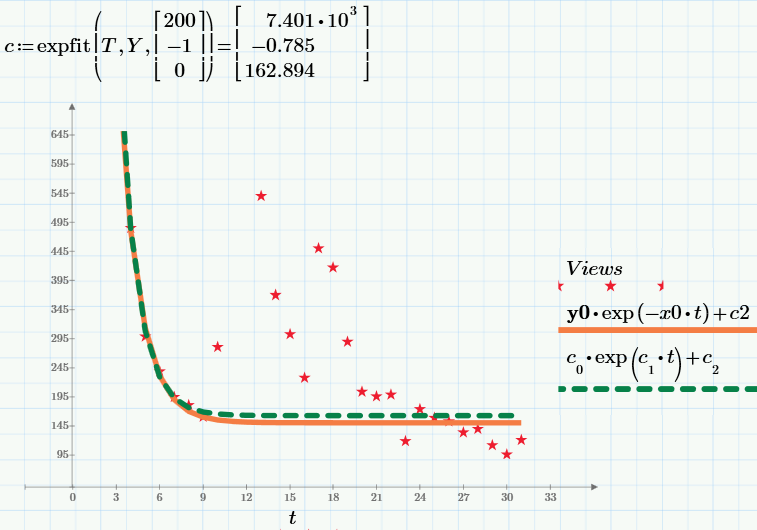
Все картинки — это скриншоты Mathcad Express (сами расчеты можете взять здесь, повторить, а при желании изменить и использовать для своих нужд). Не забудьте в начале расчетов задать с2=0 или с2=150, чтобы выбрать первую или вторую модель соответственно.
Когда известно, что случайная величина y зависит от чего-то (например, от времени или от другой случайной величины x) линейно, т.е. по закону y(x)= Ax+b, то применяется линейная регрессия (так в прошлой статье мы строили зависимость числа регистраций от числа просмотров). Для линейной регрессии коэффициенты A и b вычисляются по известным формулам. В случае регрессии другого вида, например, экспоненциальной, для того чтобы определить неизвестные параметры, необходимо решить соответствующую оптимизационную задачу: а именно, в рамках метода наименьших квадратов (МНК) задачу нахождения минимума суммы квадратов (y(xi) — yi)2.
Итак, вот данные, которые будем использовать в качестве примера. Пики посещаемости (ряд Views, красный пунктир) приходятся на моменты выхода статей. Второй ряд данных (Regs, с множителем 100) показывает число читателей, выполнивших после прочтения определенное действие (регистрацию и скачивание Mathcad Express – с его помощью, к слову, вы сможете повторить все расчеты этой и предыдущих статей). Все картинки — это скриншоты Mathcad Express, а файл с расчетами вы можете взять здесь.

Зеленой стрелкой на графике я обозначил фрагмент данных, для которого мы будем строить нелинейную регрессию. Согласно модели, которую мы примем за основу, после короткого переходного периода после выхода публикации, количество просмотров уменьшается со временем приблизительно по экспоненциальному закону:
Views ≈ C0∙exp(C1∙t).
Обоснование этой модели пока отложим до одной из будущих статей, когда речь пойдет о пуассоновском случайном процессе.
Понятно, что для анализа нужно выбрать тот фрагмент, который соответствует модели (на слишком близко к начальному пику и без суммирования со статистикой посещений после выхода второй статьи). Именно этот промежуток выделен зеленой стрелкой на первом графике, а в более крупном масштабе он выглядит вот так:

Экспоненциальная регрессия, напомню, определит график такой экспоненциальной функции, который будет «в среднем» ближе всего располагаться к показанным экспериментальным точкам. Для того чтобы найти коэффициенты регрессии, необходимо будет решить оптимизационную задачу на отыскание минимума целевой функции:
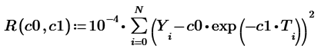
(T,Y) – массив из N экспериментальных точек, а множитель мы ввели для удобства (он не влияет на положение минимума). Дальше, конечно, можно было бы сразу написать одну-две строчки кода со встроенной функцией поиска минимума для получения искомых С0 и С1, однако, мы используем бесплатный Mathcad Express, где все они выключены, поэтому пойдем чуть более громоздким (зато более простым для понимания и наглядным) путем.
Для начала, посмотрим, как ведет себя функция R(c0, c1). Для этого зафиксируем несколько значений с0 и построим для каждого из них график функции одной переменной R(c0, х).
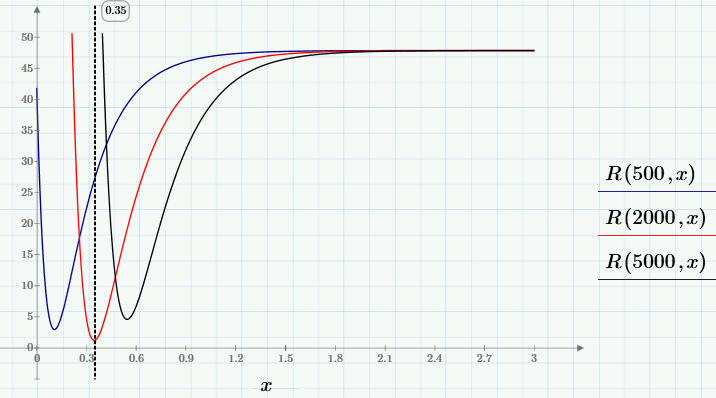
Видно, что для выбранных с0 любой из графиков семейства имеет один минимум, положение которого х зависит от с0, т.е. можно записать x=g(c0). Самый глубокий минимум, т.е., минимум R(c0, g(c0))~min будет искомым глобальным минимумом. Его-то нам и надо найти для решения задачи. Чтобы найти глобальный минимум, сначала (средствами, доступными в Mathcad Express) определим пользовательскую функцию g(y), а потом найдем минимум R(y, g(y)).
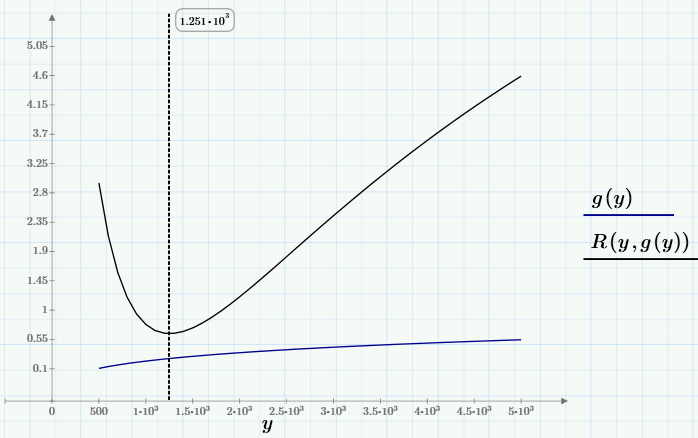
Не буду останавливаться на численном алгоритме вычисления минимума (кому интересно, он приведен в первой строчке следующего скриншота). Решение задачи (точка, в выбранных обозначениях с0=y0 и с1=х0), значение целевой функции в этой точке и график регрессии приведен ниже:
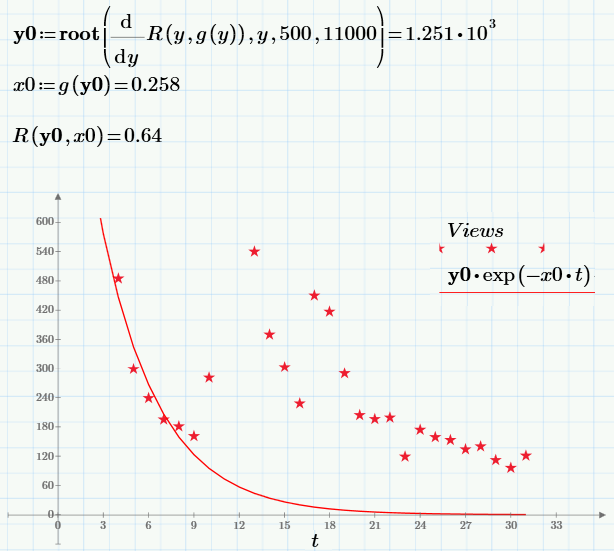
Может ли нас удовлетворить полученный результат? Скорее нет, поскольку построенная регрессия не очень хорошо ложится на экспериментальные точки. Мешает «хвост», который сильно отличается у регрессии (экспонента быстро падает почти до нуля) и данных (как видно, даже по прошествии значительного времени число просмотров ненулевое, а составляет значение около сотни).
Поэтому для улучшения результата давайте усовершенствуем модель. Будем считать моделью числа просмотров статьи сумму посещений, идущих по двум каналам:
- канал с пуассоновской статистикой Views ≈ с0∙exp(с1∙t);
- канал с приблизительно постоянным числом просмотров (назовем его параметром с2).
Этот третий параметр с2 как раз можно определить из анализа «хвоста» данных, когда пуассоновских посетителей практически нет, просто как среднее значение просмотров за последние 10 дней наблюдений.
Наконец, зная с2, можно построить уточненную регрессию вида
Views ≈ с0∙exp(с1∙t)+с2,
полностью повторив описанный выше алгоритм:
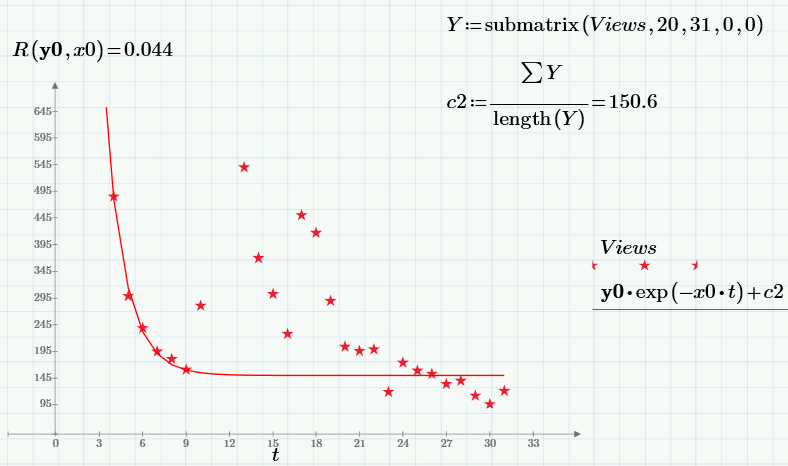
Обратите внимание на то, что значение целевой функции в минимуме (т.е. сумма квадратов невязок) снижается по сравнению со случаем с2=0 больше, чем на порядок!
В заключение, приведу результат работы встроенной функции expfit для нахождения экспоненциальной регрессии (имеющейся в коммерческой версии Mathcad Prime). Результат работы показан на графике зеленым пунктиром, а наш результат (тот же, что и на предыдущем графике) – красной сплошной линией.
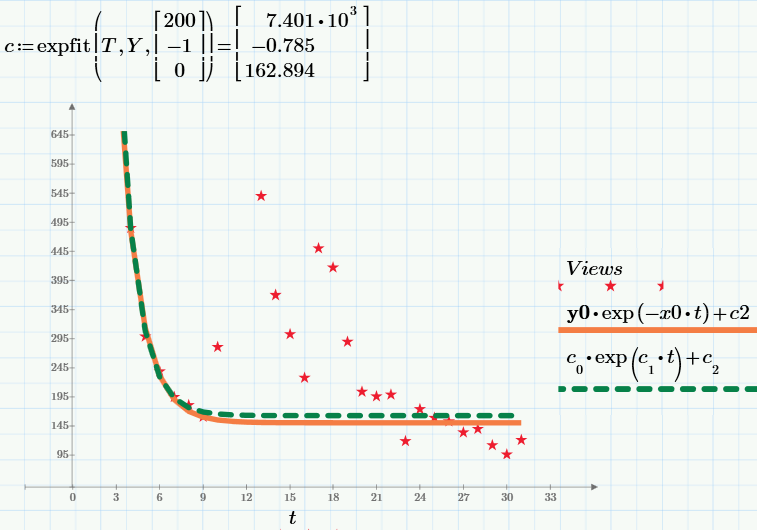
Все картинки — это скриншоты Mathcad Express (сами расчеты можете взять здесь, повторить, а при желании изменить и использовать для своих нужд). Не забудьте в начале расчетов задать с2=0 или с2=150, чтобы выбрать первую или вторую модель соответственно.