Продолжаю зарисовки об использовании бесплатного математического редактора Mathcad Express. На этот раз предлагаю обратиться к численному решению дифференциальных уравнений (в сегодняшнем примере — с частными производными). Файл с дальнейшими расчетами в форматах Mathcad и XPS вы найдете здесь.
В этой статье рассмотрим, как можно посчитать в Mathcad Express дифференциальное уравнение диффузии тепла при помощи самой простой явной разностной схемы и остановимся на свойстве устойчивости разностных схем. Речь пойдет о том, как получить вот такое решение уравнения, моделирующего остывание одномерного объекта:
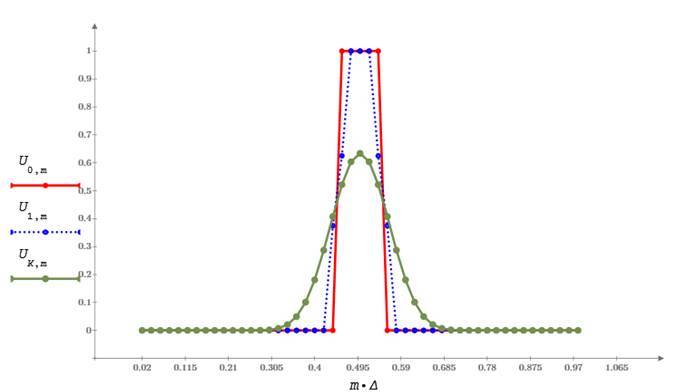
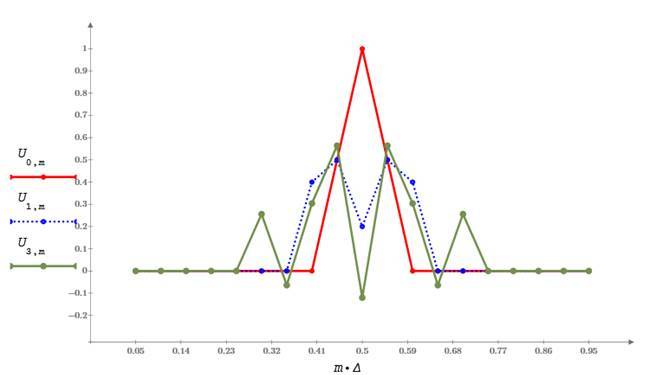
На графике показано начальное распределение температуры вдоль оси Х (красная линия) и два расчетных профиля – после первого шага и после нескольких шагов по времени.
В качестве примера дифференциального уравнения в частных производных мы рассматриваем уравнение теплопроводности (или, по-другому, диффузии тепла).
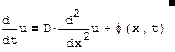
Это уравнение параболического типа, содержащее первую производную по времени t и вторую по пространственной координате x. Оно описывает динамику температуры u(x,t) в присутствии источников тепла, например, при нагреве металлического стержня. Таким образом, неизвестной функцией, подлежащей определению, является функция u(x,t). Это уравнение линейно, если источник и коэффициент диффузии D либо не зависят от температуры, либо источник зависит от нее линейно, т.к. в этом случае неизвестная функция u(x,t) (и все ее производные) входит в уравнение в первой степени.
Линейное уравнение теплопроводности имеет аналитическое решение, в то время, как подавляющее большинство нелинейных уравнений в частных производных можно решить только численно. Для того, чтобы уравнения в частных производных имело единственное решение, необходимо поставить нужное количество начальных и граничных условий, т.е., в данном случае, соотношения типа u(x,0)=Init(x) (начальное условие) вместе с u(0,t)=f1(t) и u(L,t)=f2(t) (граничные условия, если уравнение решается на интервале от 0 до L).
В приведенной интерпретации одномерное уравнение диффузии тепла описывает динамику температуры некоторого удлиненного тела, например, металлического стержня:
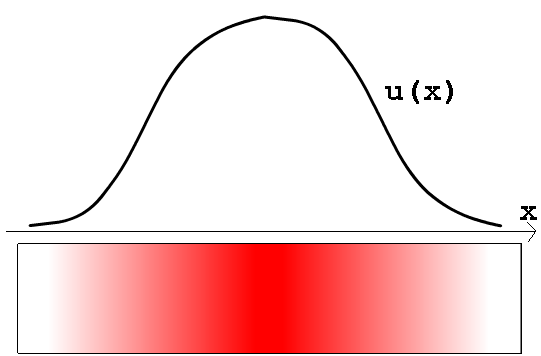
Мы будем рассматривать случай нулевого источника тепла, а в качестве начального условия выберем некоторый реалистичный профиль температуры (стержень, сильно нагретый в центре). В качестве граничных условий зададим поддержание краев стержня при постоянной температуре. Разумеется, динамика решения описывает ожидаемую картину выравнивания температуры стержня со временем (за счет перетекания тепла от центра к периферии стержня благодаря механизму теплопроводности). Скорость передачи тепла определяется значением коэффициента диффузии D. (Заинтересовавшемуся читателю я предлагаю поэкспериментировать с прилагаемыми расчетами в Mathcad Express, выбирая различные значения коэффициента диффузии).
Покажем, как реализовывать в Mathcad основной вычислительный подход к решению уравнений в частных производных – метод сеток. Будем делать это «вручную», чтобы не выйти за рамки бесплатной версии Mathcad Express.
Суть метода сеток заключается в покрытии расчетной области (x,t) сеткой из МхN точек, что определит шаги по времени и пространству τ и Δ соответственно. Тем самым, определяются узлы, в которых будет осуществляться поиск решения. Затем надо заменить дифференциальное уравнения аппроксимирующим его уравнением в конечных разностях, для каждого (i,n)-го узла сетки. В случае уравнения теплопроводности достаточно просто заменить первую производную по времени и вторую по пространству их разностными аналогами (такой метод дискретизации называют методом Эйлера, а получившуюся систему разностных уравнений – разностной схемой).
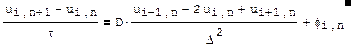
Выписанная схема является явной, т.к. в ней неизвестное значение искомой функции (на n+1 шаге по времени) можно выразить через уже вычисленные ранее значения функции на предыдущем n-м шаге («слое») по времени. Более того, т.к. и на каждом слое уравнения связаны между собой рекуррентно, т.е. значение в каждом неизвестном узле на n-м слое можно найти, зная только вычисленные ранее значения с предыдущего слоя. Это позволяет организовать процесс т.н. «бегущего счета», решая соответствующие уравнения на каждом слое (исходя из известного решения на предыдущем слое).
Следующий расчет реализует описанный алгоритм разностной явной схемы бегущего счета в Mathcad Express:
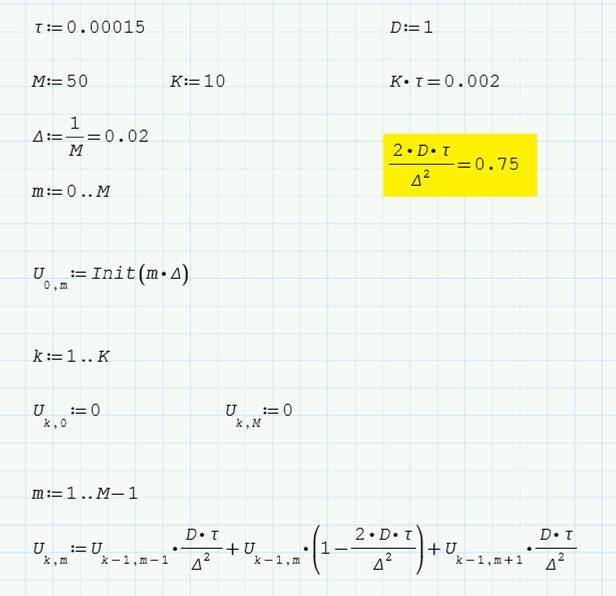
Собственно, вычисленные значения матрицы U и приведены на графике, который был показан в самом начале статьи (до ката).
В заключение, остановимся на свойстве устойчивости разностных схем. Параметр задачи, который характеризует отношение шагов разностной схемы по пространству и времени, называется коэффициентом (или «числом») Куранта:
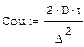
Существенно, что предыдущие расчеты по явной схеме проводились при соотношении Куранта менее 1. А вот если попробовать увеличить шаг по времени в явной схеме, так, чтобы соотношение Куранта стало больше 1, то мы столкнемся с катастрофой: решение «разваливается», и вместо ожидаемого (и просчитанного при меньших соотношениях Куранта случаях) решения получается быстроосцилирующее, совершенно неправдоподобное решение.
Этот пример демонстрирует важное свойство разностных схем, называемое устойчивостью. Оказывается, многие схемы (безусловно, или при определенном соотношении параметров, как наша схема) им не обладают, и применять такие схемы для решения задач нельзя.
Более подробную информацию о разностных схемах и примерах их расчета в Mathcad читатель может найти в моей книге по вычислительной физике (разностным схемам посвящены главы 5 и 6, книга в свободном доступе). В частности, предлагаю попробовать решить разностным методом «обратное уравнение теплопроводности», которое получается заменой переменной t на -t и которое (по идее) должно описывать реконструкцию исходного профиля температуры стержня по данным наблюдения через некоторое время.
И повторюсь, что файл с расчетами, описанными в этой статье, вы найдете здесь, а дистрибутив Mathcad Express можно скачать по ссылке.
В этой статье рассмотрим, как можно посчитать в Mathcad Express дифференциальное уравнение диффузии тепла при помощи самой простой явной разностной схемы и остановимся на свойстве устойчивости разностных схем. Речь пойдет о том, как получить вот такое решение уравнения, моделирующего остывание одномерного объекта:

На графике показано начальное распределение температуры вдоль оси Х (красная линия) и два расчетных профиля – после первого шага и после нескольких шагов по времени.
Уравнение теплопроводности
В качестве примера дифференциального уравнения в частных производных мы рассматриваем уравнение теплопроводности (или, по-другому, диффузии тепла).
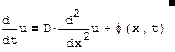
Это уравнение параболического типа, содержащее первую производную по времени t и вторую по пространственной координате x. Оно описывает динамику температуры u(x,t) в присутствии источников тепла, например, при нагреве металлического стержня. Таким образом, неизвестной функцией, подлежащей определению, является функция u(x,t). Это уравнение линейно, если источник и коэффициент диффузии D либо не зависят от температуры, либо источник зависит от нее линейно, т.к. в этом случае неизвестная функция u(x,t) (и все ее производные) входит в уравнение в первой степени.
Линейное уравнение теплопроводности имеет аналитическое решение, в то время, как подавляющее большинство нелинейных уравнений в частных производных можно решить только численно. Для того, чтобы уравнения в частных производных имело единственное решение, необходимо поставить нужное количество начальных и граничных условий, т.е., в данном случае, соотношения типа u(x,0)=Init(x) (начальное условие) вместе с u(0,t)=f1(t) и u(L,t)=f2(t) (граничные условия, если уравнение решается на интервале от 0 до L).
В приведенной интерпретации одномерное уравнение диффузии тепла описывает динамику температуры некоторого удлиненного тела, например, металлического стержня:

Мы будем рассматривать случай нулевого источника тепла, а в качестве начального условия выберем некоторый реалистичный профиль температуры (стержень, сильно нагретый в центре). В качестве граничных условий зададим поддержание краев стержня при постоянной температуре. Разумеется, динамика решения описывает ожидаемую картину выравнивания температуры стержня со временем (за счет перетекания тепла от центра к периферии стержня благодаря механизму теплопроводности). Скорость передачи тепла определяется значением коэффициента диффузии D. (Заинтересовавшемуся читателю я предлагаю поэкспериментировать с прилагаемыми расчетами в Mathcad Express, выбирая различные значения коэффициента диффузии).
Разностная схема
Покажем, как реализовывать в Mathcad основной вычислительный подход к решению уравнений в частных производных – метод сеток. Будем делать это «вручную», чтобы не выйти за рамки бесплатной версии Mathcad Express.
Суть метода сеток заключается в покрытии расчетной области (x,t) сеткой из МхN точек, что определит шаги по времени и пространству τ и Δ соответственно. Тем самым, определяются узлы, в которых будет осуществляться поиск решения. Затем надо заменить дифференциальное уравнения аппроксимирующим его уравнением в конечных разностях, для каждого (i,n)-го узла сетки. В случае уравнения теплопроводности достаточно просто заменить первую производную по времени и вторую по пространству их разностными аналогами (такой метод дискретизации называют методом Эйлера, а получившуюся систему разностных уравнений – разностной схемой).
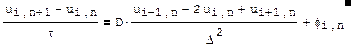
Выписанная схема является явной, т.к. в ней неизвестное значение искомой функции (на n+1 шаге по времени) можно выразить через уже вычисленные ранее значения функции на предыдущем n-м шаге («слое») по времени. Более того, т.к. и на каждом слое уравнения связаны между собой рекуррентно, т.е. значение в каждом неизвестном узле на n-м слое можно найти, зная только вычисленные ранее значения с предыдущего слоя. Это позволяет организовать процесс т.н. «бегущего счета», решая соответствующие уравнения на каждом слое (исходя из известного решения на предыдущем слое).
Следующий расчет реализует описанный алгоритм разностной явной схемы бегущего счета в Mathcad Express:

Собственно, вычисленные значения матрицы U и приведены на графике, который был показан в самом начале статьи (до ката).
Устойчивость
В заключение, остановимся на свойстве устойчивости разностных схем. Параметр задачи, который характеризует отношение шагов разностной схемы по пространству и времени, называется коэффициентом (или «числом») Куранта:
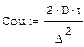
Существенно, что предыдущие расчеты по явной схеме проводились при соотношении Куранта менее 1. А вот если попробовать увеличить шаг по времени в явной схеме, так, чтобы соотношение Куранта стало больше 1, то мы столкнемся с катастрофой: решение «разваливается», и вместо ожидаемого (и просчитанного при меньших соотношениях Куранта случаях) решения получается быстроосцилирующее, совершенно неправдоподобное решение.

Этот пример демонстрирует важное свойство разностных схем, называемое устойчивостью. Оказывается, многие схемы (безусловно, или при определенном соотношении параметров, как наша схема) им не обладают, и применять такие схемы для решения задач нельзя.
Более подробную информацию о разностных схемах и примерах их расчета в Mathcad читатель может найти в моей книге по вычислительной физике (разностным схемам посвящены главы 5 и 6, книга в свободном доступе). В частности, предлагаю попробовать решить разностным методом «обратное уравнение теплопроводности», которое получается заменой переменной t на -t и которое (по идее) должно описывать реконструкцию исходного профиля температуры стержня по данным наблюдения через некоторое время.
И повторюсь, что файл с расчетами, описанными в этой статье, вы найдете здесь, а дистрибутив Mathcad Express можно скачать по ссылке.