Доброго времени суток, Хабрапользователи!
Визуальная криптография [1] впервые была введена Мони Наором и Ади Шамиром в 1994 году [3]. Она используется для шифрования изображения или текста, представленного в виде изображения. Основная идея модели визуальной криптографии состоит в разбиении исходного изображения на несколько шифрованных («теневых» изображений, shadow images), каждое из которых не дает никакой информации об исходном изображении кроме, может быть, его размера (изображение – а-ля «белый шум»). При наложении шифрованных изображений друг на друга, можно получить исходное изображение. Таким образом, для декодирования не требуется специальных знаний, высокопроизводительных вычислений и даже компьютера (в случае, если распечатать теневые изображения на прозрачных пленках). В случае использования этого алгоритма в компьютерных системах, наложить все части изображения друг на друга можно используя логические операции AND, OR, XOR (или установив более высокую степень прозрачности в графическом редакторе). Данная технология обладает криптоустойчивостью за счет того, что при разделении исходного изображения на множество шифроизображений происходит случайным образом.
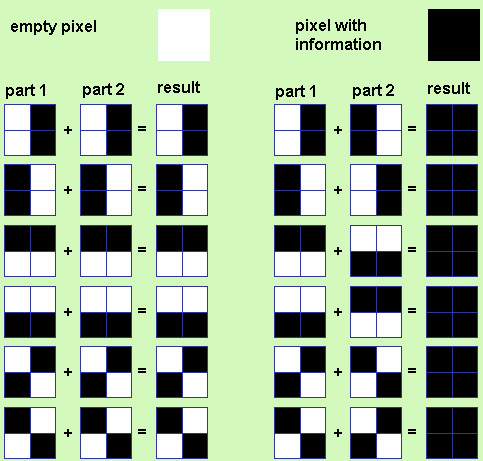
Рисунок 1. Возможные состояния пикселя при (2, 2)-визуальной схеме секретного обмена
Приложением таких технологий является защита от копирования и проверка подлинности (авторских прав, watermarking), отслеживание электронных бланков при удаленном голосовании, шифрование финансовых документов, управление ключами доступа и совместное использование паролей.
Наор и Шамир продемонстрировали (k, n)-визуальную схему секретного обмена, где изображение было разбито на n частей, таким образом, что кто-либо, обладавший любыми k частями мог расшифровать его, в то время как любые k-1 частей не давали никакой информации о содержании исходного изображения. Когда все k частей будут наложены друг на друга, мы увидим исходное изображение [3].
Для того чтобы разбить исходное черно-белое изображение на n частей, каждый пиксель изображения представляется в виде некоторого количества меньших частей (subpixels). Количество белых и черных частей всегда одинаковое. Если пиксель делится на две части, то получается один белый и один черный блок. Если пиксель делится на четыре равные части, то получаем два белых и два черных блока.
Рассмотрим (2, 2)-визуальную схему секретного обмена, т.е. исходное изображение разбивается на два теневых изображения, каждое из которых представляет собой изображение белого шума, но при наложении дают исходное изображении. Каждый пиксель исходного изображения будем разбивать на четыре части, таким образом, если размер исходного изображения был M×N, то размеры теневых изображений будут 2M×2N.
На рисунке 1 показано, что пиксель, разделенный на четыре части, может иметь шесть разных состояний.
Если пиксель на первом слое имеет одно положение, пиксель на втором слое в свою очередь может иметь два положения: идентичное либо инвертированное пикселю первого слоя. Если пиксель части 2 идентичен пикселю части 1, то пиксель, полученный в результате наложения обоих теневых изображений, будет наполовину белый и наполовину черный. Такой пиксель называют серым или пустым. Если пиксели части 1 и части 2 противоположны, то пиксель, полученный в результате наложения, будет полностью черным. Он будет являться информационным.
Опишем процесс получения теневых изображений для исходного изображения для схемы (2, 2): для каждого пикселя исходного изображения, для первого теневого изображения случайным образом выбирается одно из шести возможных состояний пикселя, приведенных на рисунке 1. Состояние пикселя второго теневого изображения выбирается идентичным или симметричным состоянию пикселя первой «тени» в зависимости от того, белый или черный это был пиксель в исходном изображении соответственно. Схожим образом можно построить любую (k, n) визуальную схему секретного обмена [3].
Теоретически, этот алгоритм может быть эффективно использован для безопасного обмена сообщениями по сети, если множество возможных сообщений не очень большое (например, множество различных сигналов тревоги). Реализовать такой обмен можно следующим образом.
Пусть и на стороне источника сообщений имеются только все первые теневые изображения из пары (изображения 1), а на стороне приемника сообщений – только все вторые изображения из пары теневых изображений (изображения 2). Каждое теневое изображение – совершенно случайное и, при попадании в руки злоумышленника в отдельности (без второго изображения из пары), не дает никакой информации. При получении одного из теневых изображений 1 приемник последовательно накладывает его на изображения из своего множества и находит первое семантически нагруженное изображение-сообщение (исходящий от источника сообщений конкретный тревожный сигнал).
Matlab-функция, выполняющая разделения исходного двоичного изображения на два теневых «в лоб», использующая 4 (из 6 возможных, см. рис. 6) состояния пикселя будет иметь следующий вид:
Функция
Ниже приведен код Matlab-скрипта, демонстрирующий работу алгоритма разделения секретной визуальной информации.
Ниже приведены результаты выполнение операции кодирования и декодирования исходного «секретного» изображения. Рассматриваются различные операции совмещения полученных из исходного теневых изображений: с помощью XOR (Рис. 6), AND (Рис. 7) и OR (Рис. 8).

Рисунок 2. Исходное изображение

Рисунок 3. После преобразования изображения в ч/б

Рисунок 4. Теневое изображение 1

Рисунок 5. Теневое изображение 2

Рисунок 6. Результат для NOT(XOR(S1, S2))

Рисунок 7. Результат для AND(S1, S2)

Рисунок 8. Результат для OR(S1, S2)
(k, n)-визуальная схема разделения секретной информации является криптостойкой до тех пор, пока k частей изображения не попадут в руки злоумышленника. Если же перехвачено менее k частей, то расшифровка исходного изображения – невозможна.
Если в процессе использования данной системы полностью соблюдается случайный подход к разбитию пикселей на блоки, то визуальная криптография предлагает абсолютную надежность и секретность.
Здесь был рассмотрен классический алгоритм визуальной криптографии. На сегодняшний день существует множество улучшенных моделей этого алгоритма, например, для кодирования цветных изображений [4, 6], или схемы, где, вместо теневых изображений в виде белого шума, используются семантически значимые изображения [5], а также схемы визуальной криптографии на основе техник стеганографии [2, 7].
1. en.wikipedia.org/wiki/Visual_cryptography
2. ru.wikipedia.org/wiki/%D0%A1%D1%82%D0%B5%D0%B3%D0%B0%D0%BD%D0%BE%D0%B3%D1%80%D0%B0%D1%84%D0%B8%D1%8F
3. M. Naor and A. Shamir. Visual cryptography. In EUROCRYPT’94. — Springer-Verlag Berlin, 1995.
4. D. Jin, W.Q. Yan, and M.S. Kankanhalli. Progressive color visual cryptography. In Journal Of Electronic Imaging, 2005.— Vol. 14, Issue 3.
5. Feng Liu and ChuanKun Wu. Embedded extended visual cryptography schemes. — China, 2006.
6. Y.C. Hou. Visual cryptography for color images. In Pattern Recognition, 2003.
7. Ritesh Murherjee, Nabin Ghoshal. Steganography based visual cryptography. – Berlin: Springer-Verlag, 2013.
Визуальная криптография [1] впервые была введена Мони Наором и Ади Шамиром в 1994 году [3]. Она используется для шифрования изображения или текста, представленного в виде изображения. Основная идея модели визуальной криптографии состоит в разбиении исходного изображения на несколько шифрованных («теневых» изображений, shadow images), каждое из которых не дает никакой информации об исходном изображении кроме, может быть, его размера (изображение – а-ля «белый шум»). При наложении шифрованных изображений друг на друга, можно получить исходное изображение. Таким образом, для декодирования не требуется специальных знаний, высокопроизводительных вычислений и даже компьютера (в случае, если распечатать теневые изображения на прозрачных пленках). В случае использования этого алгоритма в компьютерных системах, наложить все части изображения друг на друга можно используя логические операции AND, OR, XOR (или установив более высокую степень прозрачности в графическом редакторе). Данная технология обладает криптоустойчивостью за счет того, что при разделении исходного изображения на множество шифроизображений происходит случайным образом.

Рисунок 1. Возможные состояния пикселя при (2, 2)-визуальной схеме секретного обмена
Приложением таких технологий является защита от копирования и проверка подлинности (авторских прав, watermarking), отслеживание электронных бланков при удаленном голосовании, шифрование финансовых документов, управление ключами доступа и совместное использование паролей.
Алгоритм визуальной криптографии
Наор и Шамир продемонстрировали (k, n)-визуальную схему секретного обмена, где изображение было разбито на n частей, таким образом, что кто-либо, обладавший любыми k частями мог расшифровать его, в то время как любые k-1 частей не давали никакой информации о содержании исходного изображения. Когда все k частей будут наложены друг на друга, мы увидим исходное изображение [3].
Для того чтобы разбить исходное черно-белое изображение на n частей, каждый пиксель изображения представляется в виде некоторого количества меньших частей (subpixels). Количество белых и черных частей всегда одинаковое. Если пиксель делится на две части, то получается один белый и один черный блок. Если пиксель делится на четыре равные части, то получаем два белых и два черных блока.
Рассмотрим (2, 2)-визуальную схему секретного обмена, т.е. исходное изображение разбивается на два теневых изображения, каждое из которых представляет собой изображение белого шума, но при наложении дают исходное изображении. Каждый пиксель исходного изображения будем разбивать на четыре части, таким образом, если размер исходного изображения был M×N, то размеры теневых изображений будут 2M×2N.
На рисунке 1 показано, что пиксель, разделенный на четыре части, может иметь шесть разных состояний.
Если пиксель на первом слое имеет одно положение, пиксель на втором слое в свою очередь может иметь два положения: идентичное либо инвертированное пикселю первого слоя. Если пиксель части 2 идентичен пикселю части 1, то пиксель, полученный в результате наложения обоих теневых изображений, будет наполовину белый и наполовину черный. Такой пиксель называют серым или пустым. Если пиксели части 1 и части 2 противоположны, то пиксель, полученный в результате наложения, будет полностью черным. Он будет являться информационным.
Опишем процесс получения теневых изображений для исходного изображения для схемы (2, 2): для каждого пикселя исходного изображения, для первого теневого изображения случайным образом выбирается одно из шести возможных состояний пикселя, приведенных на рисунке 1. Состояние пикселя второго теневого изображения выбирается идентичным или симметричным состоянию пикселя первой «тени» в зависимости от того, белый или черный это был пиксель в исходном изображении соответственно. Схожим образом можно построить любую (k, n) визуальную схему секретного обмена [3].
Теоретически, этот алгоритм может быть эффективно использован для безопасного обмена сообщениями по сети, если множество возможных сообщений не очень большое (например, множество различных сигналов тревоги). Реализовать такой обмен можно следующим образом.
Пусть и на стороне источника сообщений имеются только все первые теневые изображения из пары (изображения 1), а на стороне приемника сообщений – только все вторые изображения из пары теневых изображений (изображения 2). Каждое теневое изображение – совершенно случайное и, при попадании в руки злоумышленника в отдельности (без второго изображения из пары), не дает никакой информации. При получении одного из теневых изображений 1 приемник последовательно накладывает его на изображения из своего множества и находит первое семантически нагруженное изображение-сообщение (исходящий от источника сообщений конкретный тревожный сигнал).
Matlab-реализация алгоритма
Matlab-функция, выполняющая разделения исходного двоичного изображения на два теневых «в лоб», использующая 4 (из 6 возможных, см. рис. 6) состояния пикселя будет иметь следующий вид:
function [S1,S2] =getShdwImg(Img)
% получение теневых изображений S1 и S2 из исходного бинарного изображения (Img)
%
% получаем размер исходного изображения
[m,n] = size(Img);
% запасаемся памятью для каждого теневого изображения :)
S1= zeros(2*m,2*n);
S2= zeros(2*m,2*n);
% для каждого пикселя исходного изображения - действуем согласно Рис. 1
% Примечание:
for i=1:m-1
for j=1:n-1
r = randi(4);
if(Img(i,j)==1)
switch r
case 1,
S1(2*i,2*j)=1;
S1(2*i+1,2*j)=1;
S1(2*i,2*j+1)=0;
S1(2*i+1,2*j+1)=0;
S2(2*i,2*j)=1;
S2(2*i+1,2*j)=1;
S2(2*i,2*j+1)=0;
S2(2*i+1,2*j+1)=0;
case 2,
S1(2*i,2*j)=0;
S1(2*i+1,2*j)=0;
S1(2*i,2*j+1)=1;
S1(2*i+1,2*j+1)=1;
S2(2*i,2*j)=0;
S2(2*i+1,2*j)=0;
S2(2*i,2*j+1)=1;
S2(2*i+1,2*j+1)=1;
case 3,
S1(2*i,2*j)=0;
S1(2*i+1,2*j)=1;
S1(2*i,2*j+1)=1;
S1(2*i+1,2*j+1)=0;
S2(2*i,2*j)=0;
S2(2*i+1,2*j)=1;
S2(2*i,2*j+1)=1;
S2(2*i+1,2*j+1)=0;
case 4,
S1(2*i,2*j)=1;
S1(2*i+1,2*j)=0;
S1(2*i,2*j+1)=0;
S1(2*i+1,2*j+1)=1;
S2(2*i,2*j)=1;
S2(2*i+1,2*j)=0;
S2(2*i,2*j+1)=0;
S2(2*i+1,2*j+1)=1;
end
else
switch r
case 1,
S1(2*i,2*j)=1;
S1(2*i+1,2*j)=1;
S1(2*i,2*j+1)=0;
S1(2*i+1,2*j+1)=0;
S2(2*i,2*j)=0;
S2(2*i+1,2*j)=0;
S2(2*i,2*j+1)=1;
S2(2*i+1,2*j+1)=1;
case 2,
S1(2*i,2*j)=0;
S1(2*i+1,2*j)=0;
S1(2*i,2*j+1)=1;
S1(2*i+1,2*j+1)=1;
S2(2*i,2*j)=1;
S2(2*i+1,2*j)=1;
S2(2*i,2*j+1)=0;
S2(2*i+1,2*j+1)=0;
case 3,
S1(2*i,2*j)=0;
S1(2*i+1,2*j)=1;
S1(2*i,2*j+1)=1;
S1(2*i+1,2*j+1)=0;
S2(2*i,2*j)=1;
S2(2*i+1,2*j)=0;
S2(2*i,2*j+1)=0;
S2(2*i+1,2*j+1)=1;
case 4,
S1(2*i,2*j)=1;
S1(2*i+1,2*j)=0;
S1(2*i,2*j+1)=0;
S1(2*i+1,2*j+1)=1;
S2(2*i,2*j)=0;
S2(2*i+1,2*j)=1;
S2(2*i,2*j+1)=1;
S2(2*i+1,2*j+1)=0;
end
end
end
end
Функция
getShdwImg разбивает исходное изображение так, как показано на Рис. 1, с единственной разницей только в том, что в двоичных изображениях Matlab — черные пиксели изображения равну нулю, а белые, соответственно, равны единице.Ниже приведен код Matlab-скрипта, демонстрирующий работу алгоритма разделения секретной визуальной информации.
close all
% считываем исходное RGB-изображение и преобразуем его в бинарное
biImg = imread('nordavind_logo.jpg');
biImg = rgb2gray(biImg);
level = graythresh(biImg); % пороговая фильтрация по Отсу (Otsu)
biImg = im2bw(biImg,level);
% выводим результат на экран
figure(1)
imshow(biImg);
title(['Original binary image']);
% получаем два теневых изображения
[S1,S2] =getShdwImg(biImg);
% выводим их на экран
figure(2)
imshow(S1);
title(['Shadow image S1']);
%
figure(3)
imshow(S2);
title(['Shadow image S2']);
% выводим на экран результат их наложения друг на друга
% различными способами
figure(4)
% imshow(or(S1, S2));
% imshow(and(S1,S2));
imshow(~xor(S1, S2)); % операция “~”(NOT) используется, чтобы получить черный текст на белом фоне, а не наоборот
title(['Superimposed image']);
Результаты
Ниже приведены результаты выполнение операции кодирования и декодирования исходного «секретного» изображения. Рассматриваются различные операции совмещения полученных из исходного теневых изображений: с помощью XOR (Рис. 6), AND (Рис. 7) и OR (Рис. 8).

Рисунок 2. Исходное изображение

Рисунок 3. После преобразования изображения в ч/б

Рисунок 4. Теневое изображение 1

Рисунок 5. Теневое изображение 2

Рисунок 6. Результат для NOT(XOR(S1, S2))

Рисунок 7. Результат для AND(S1, S2)

Рисунок 8. Результат для OR(S1, S2)
Заключение
(k, n)-визуальная схема разделения секретной информации является криптостойкой до тех пор, пока k частей изображения не попадут в руки злоумышленника. Если же перехвачено менее k частей, то расшифровка исходного изображения – невозможна.
Если в процессе использования данной системы полностью соблюдается случайный подход к разбитию пикселей на блоки, то визуальная криптография предлагает абсолютную надежность и секретность.
Здесь был рассмотрен классический алгоритм визуальной криптографии. На сегодняшний день существует множество улучшенных моделей этого алгоритма, например, для кодирования цветных изображений [4, 6], или схемы, где, вместо теневых изображений в виде белого шума, используются семантически значимые изображения [5], а также схемы визуальной криптографии на основе техник стеганографии [2, 7].
Ссылки
1. en.wikipedia.org/wiki/Visual_cryptography
2. ru.wikipedia.org/wiki/%D0%A1%D1%82%D0%B5%D0%B3%D0%B0%D0%BD%D0%BE%D0%B3%D1%80%D0%B0%D1%84%D0%B8%D1%8F
3. M. Naor and A. Shamir. Visual cryptography. In EUROCRYPT’94. — Springer-Verlag Berlin, 1995.
4. D. Jin, W.Q. Yan, and M.S. Kankanhalli. Progressive color visual cryptography. In Journal Of Electronic Imaging, 2005.— Vol. 14, Issue 3.
5. Feng Liu and ChuanKun Wu. Embedded extended visual cryptography schemes. — China, 2006.
6. Y.C. Hou. Visual cryptography for color images. In Pattern Recognition, 2003.
7. Ritesh Murherjee, Nabin Ghoshal. Steganography based visual cryptography. – Berlin: Springer-Verlag, 2013.