 Здравствуйте, коллеги! Это блог открытой русскоговорящей дата саентологической ложи. Нас уже легион, точнее 2500+ человек в слаке. За полтора года мы нагенерили 800к+ сообщений (ради этого слак выделил нам корпоративный аккаунт). Наши люди есть везде и, может, даже в вашей организации. Если вы интересуетесь машинным обучением, но по каким-то причинам не знаете про Open Data Science, то возможно вы в курсе мероприятий, которые организовывает сообщество. Самым масштабным из них является DataFest, который проходил недавно в офисе Mail.Ru Group, за два дня его посетило 1700 человек. Мы растем, наши ложи открываются в городах России, а также в Нью-Йорке, Дубае и даже во Львове, да, мы не воюем, а иногда даже и употребляем горячительные напитки вместе. И да, мы некоммерческая организация, наша цель — просвещение. Мы делаем все ради искусства. (пс: на фотографии вы можете наблюдать заседание ложи в одном из тайных храмов в Москве).
Здравствуйте, коллеги! Это блог открытой русскоговорящей дата саентологической ложи. Нас уже легион, точнее 2500+ человек в слаке. За полтора года мы нагенерили 800к+ сообщений (ради этого слак выделил нам корпоративный аккаунт). Наши люди есть везде и, может, даже в вашей организации. Если вы интересуетесь машинным обучением, но по каким-то причинам не знаете про Open Data Science, то возможно вы в курсе мероприятий, которые организовывает сообщество. Самым масштабным из них является DataFest, который проходил недавно в офисе Mail.Ru Group, за два дня его посетило 1700 человек. Мы растем, наши ложи открываются в городах России, а также в Нью-Йорке, Дубае и даже во Львове, да, мы не воюем, а иногда даже и употребляем горячительные напитки вместе. И да, мы некоммерческая организация, наша цель — просвещение. Мы делаем все ради искусства. (пс: на фотографии вы можете наблюдать заседание ложи в одном из тайных храмов в Москве).Мне выпала честь сделать первый пост, и я, пожалуй, отклонюсь от своей привычной нейросетевой тематики и сделаю пост о базовых понятиях машинного обучения на примере одной из самых простых и самых полезных моделей — линейной регрессии. Я буду использовать язык питон для демонстрации экспериментов и отрисовки графиков, все это вы с легкостью сможете повторить на своем компьютере. Поехали.
Формализмы
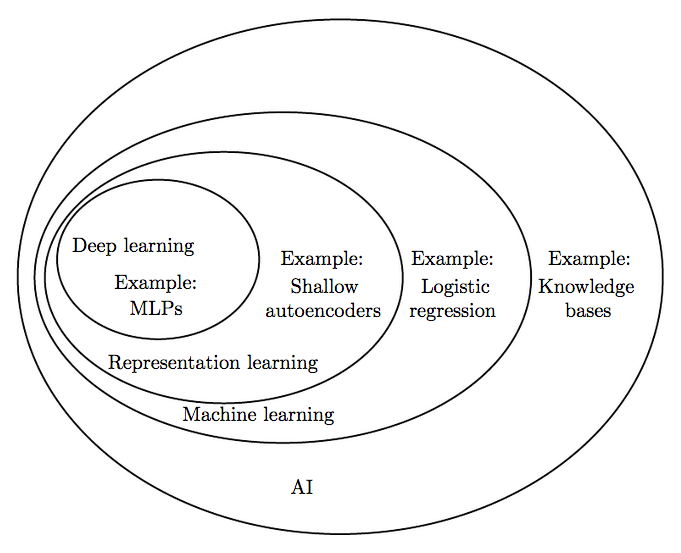
Машинное обучение — это подраздел искусственного интеллекта, в котором изучаются алгоритмы, способные обучаться без прямого программирования того, что нужно изучать. Линейная регрессия является типичным представителем алгоритмов машинного обучения. Для начала ответим на вопрос «а что вообще значит обучаться?». Ответ на этот вопрос мы возьмем из книги 1997 года (стоит отметить, что оглавление этой книги не сильно отличается от современных книг по машинному обучению).
Говорят, что программа обучается на опытеотносительно класса задач
в смысле меры качества
, если при решении задачи
качество, измеряемое мерой
, возрастает при демонстрации нового опыта
.
Можно выделить следующие задачи
У нас есть задача, данные и способ оценки программы/модели. Давайте определим, что такое модель, и что значит обучить модель. Предиктивная модель – это параметрическое семейство функций (семейство гипотез):
где
-
-
— множество параметров
Таким образом, из большого семейства гипотез мы должны выбрать какую-то одну конкретную, которая с точки зрения меры
Получается, что алгоритм обучения — это отображение из набора данных в пространство гипотез. Обычно процесс обучения с учителем состоит из двух шагов:
- обучение:
;
- применение:
.
Часто для обучения модели пользуются принципом минимизации эмпирического риска. Риском гипотезы
Но, к сожалению, такой интеграл не посчитать, т.к. распределение
Тогда, согласно принципу минимизации эмпирического риска, мы должны выбрать такую гипотезу
У данного принципа есть существенный недостаток, решения найденные таким путем будут склонны к переобучению. Мы говорим, что модель обладает обобщающей способностью, тогда, когда ошибка на новом (тестовом) наборе данных (взятом из того же распределения
Линейная регрессия
Давайте ограничим пространство гипотез только линейными функциями от
Эмпирический риск (функция стоимости) принимает форму среднеквадратичной ошибки:
строки матрицы
приравняем к нулю и найдем решение в явном виде:
Поздравляю, дамы и господа, мы только что с вами вывели алгоритм машинного обучения. Реализуем же этот алгоритм. Начнем с датасета, состоящего всего из одного признака. Будем брать случайную точку на синусе и добавлять к ней шум — таким образом получим целевую переменную; признаком в этом случае будет координата
def generate_wave_set(n_support=1000, n_train=25, std=0.3):
data = {}
# выберем некоторое количество точек из промежутка от 0 до 2*pi
data['support'] = np.linspace(0, 2*np.pi, num=n_support)
# для каждой посчитаем значение sin(x) + 1
# это будет ground truth
data['values'] = np.sin(data['support']) + 1
# из support посемплируем некоторое количество точек с возвратом, это будут признаки
data['x_train'] = np.sort(np.random.choice(data['support'], size=n_train, replace=True))
# опять посчитаем sin(x) + 1 и добавим шум, получим целевую переменную
data['y_train'] = np.sin(data['x_train']) + 1 + np.random.normal(0, std, size=data['x_train'].shape[0])
return data
data = generate_wave_set(1000, 250)
Отрисовка графика
print 'Shape of X is', data['x_train'].shape
print 'Head of X is', data['x_train'][:10]
margin = 0.3
plt.plot(data['support'], data['values'], 'b--', alpha=0.5, label='manifold')
plt.scatter(data['x_train'], data['y_train'], 40, 'g', 'o', alpha=0.8, label='data')
plt.xlim(data['x_train'].min() - margin, data['x_train'].max() + margin)
plt.ylim(data['y_train'].min() - margin, data['y_train'].max() + margin)
plt.legend(loc='upper right', prop={'size': 20})
plt.title('True manifold and noised data')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

А теперь реализуем алгоритм обучения, используя магию NumPy:
# добавим колонку единиц к единственному столбцу признаков
X = np.array([np.ones(data['x_train'].shape[0]), data['x_train']]).T
# перепишем, полученную выше формулу, используя numpy
# шаг обучения - в этом шаге мы ищем лучшую гипотезу h
w = np.dot(np.dot(np.linalg.inv(np.dot(X.T, X)), X.T), data['y_train'])
# шаг применения: посчитаем прогноз
y_hat = np.dot(w, X.T)
Отрисовка графика
margin = 0.3
plt.plot(data['support'], data['values'], 'b--', alpha=0.5, label='manifold')
plt.scatter(data['x_train'], data['y_train'], 40, 'g', 'o', alpha=0.8, label='data')
plt.plot(data['x_train'], y_hat, 'r', alpha=0.8, label='fitted')
plt.xlim(data['x_train'].min() - margin, data['x_train'].max() + margin)
plt.ylim(data['y_train'].min() - margin, data['y_train'].max() + margin)
plt.legend(loc='upper right', prop={'size': 20})
plt.title('Fitted linear regression')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

Как мы видим, линия не очень-то совпадает с настоящей кривой. Среднеквадратичная ошибка равна 0.26704 условных единиц. Очевидно, что если бы вместо линии мы использовали кривую третьего порядка, то результат был бы куда лучше. И, на самом деле, с помощью линейной регрессии мы можем обучать нелинейные модели.
Полиномиальная регрессия
В линейной регрессии мы ограничивали пространство гипотез только линейными функциями от признаков. Давайте теперь расширим пространство гипотез до всех полиномов степени
Если заранее предрассчитать все степени признаков, то задача опять сводится к описанному выше алгоритму — методу наименьших квадратов. Попробуем отрисовать графики нескольких полиномов разных степеней.
# список степеней p полиномов, который мы протестируем
degree_list = [1, 2, 3, 5, 7, 10, 13]
cmap = plt.get_cmap('jet')
colors = [cmap(i) for i in np.linspace(0, 1, len(degree_list))]
margin = 0.3
plt.plot(data['support'], data['values'], 'b--', alpha=0.5, label='manifold')
plt.scatter(data['x_train'], data['y_train'], 40, 'g', 'o', alpha=0.8, label='data')
w_list = []
err = []
for ix, degree in enumerate(degree_list):
# список с предрасчитанными степенями признака
dlist = [np.ones(data['x_train'].shape[0])] + \
map(lambda n: data['x_train']**n, range(1, degree + 1))
X = np.array(dlist).T
w = np.dot(np.dot(np.linalg.inv(np.dot(X.T, X)), X.T), data['y_train'])
w_list.append((degree, w))
y_hat = np.dot(w, X.T)
err.append(np.mean((data['y_train'] - y_hat)**2))
plt.plot(data['x_train'], y_hat, color=colors[ix], label='poly degree: %i' % degree)
Отрисовка графика
plt.xlim(data['x_train'].min() - margin, data['x_train'].max() + margin)
plt.ylim(data['y_train'].min() - margin, data['y_train'].max() + margin)
plt.legend(loc='upper right', prop={'size': 20})
plt.title('Fitted polynomial regressions')
plt.xlabel('x')
plt.ylabel('y')
plt.show()
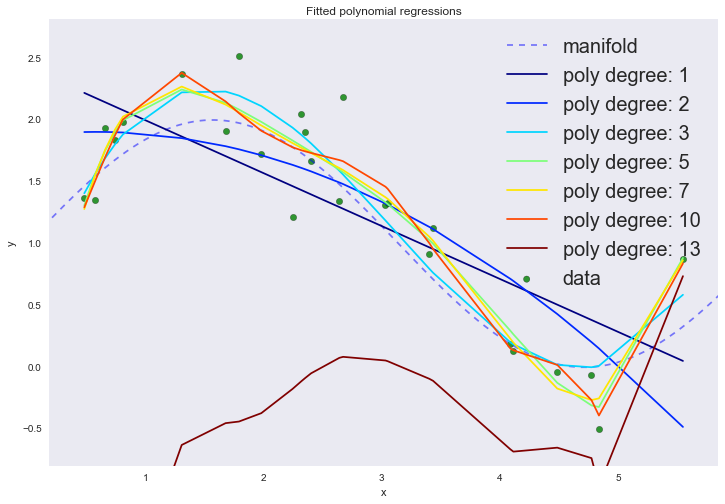
На графике мы можем наблюдать сразу два феномена. Пока не обращайте внимание на 13-ую степень полинома. При увеличении степени полинома, средняя ошибка продолжает уменьшаться, хотя мы вроде были уверены, что именно кубический полином должен лучше всего описывать наши данные.
| p | error |
|---|---|
| 1 | 0.26704 |
| 2 | 0.22495 |
| 3 | 0.08217 |
| 5 | 0.05862 |
| 7 | 0.05749 |
| 10 | 0.0532 |
| 13 | 5.76155 |
Это явный признак переобучения, который можно заметить по визуализации даже не используя тестовый набор данных: при увеличении степени полинома выше третьей модель начинает интерполировать данные, вместо экстраполяции. Другими словами, график функции проходит точно через точки из тренировочного набора данных, причем чем выше степень полинома, тем через большее количество точек он проходит. Степень полинома отражает сложность модели. Таким образом, сложные модели, у которых степеней свободы достаточно много, могут попросту запомнить весь тренировочный набор, полностью теряя обобщающую способность. Это и есть проявление негативной стороны принципа минимизации эмпирического риска.
Вернемся к полиному 13-ой степени, с ним явно что-то не так. По идее, мы ожидаем, что полином 13-ой степени будет описывать тренировочный набор данных еще лучше, но результат показывает, что это не так. Из курса линейной алгебры мы помним, что обратная матрица существует только для несингулярных матриц, т.е. тех, у которых нет линейной зависимости колонок или строк. В методе наименьших квадратов нам необходимо инвертировать следующую матрицу:
np.linalg.eigvals(np.cov(X[:, 1:].T))
Out[10]:
array([
9.29965299e+17+0.j , 4.04567033e+13+0.j ,
5.44657111e+09+0.j , 3.54104756e+06+0.j ,
8.36745166e+03+0.j , 6.82745279e+01+0.j ,
8.88434986e-01+0.j , 2.42827315e-02+0.00830052j,
2.42827315e-02-0.00830052j, 1.17621840e-03+0.j ,
1.72254789e-04+0.j , -5.68384880e-06+0.j ,
2.39611454e-07+0.j ])

Все так, numpy вернул два комплекснозначных собственных значения, что идет вразрез с теорией. Для симметричных и положительно определенных матриц (каковой и является матрица
UPDATE (один из членов ложи по имени Андрей Оськин, с ником в слаке skoffer, без аккаунта на хабре, подсказывает):
Есть только одно замечание — не надо пользоваться формулой `(X^T X^{-1}) X^T` для вычисления коэффициентов линейной регрессии. Проблема с расходящимися значениями хорошо известна и на практике используют `QR` или `SVD`.
Ну, то есть вот такой кусок кода даст вполне приличный результат:
degree = 13 dlist = [np.ones(data['x_train'].shape[0])] + \ list(map(lambda n: data['x_train']**n, range(1, degree + 1))) X = np.array(dlist).T q, r = np.linalg.qr(X) y_hat = np.dot(np.dot(q, q.T), data['y_train']) plt.plot(data['x_train'], y_hat, label='poly degree: %i' % degree)
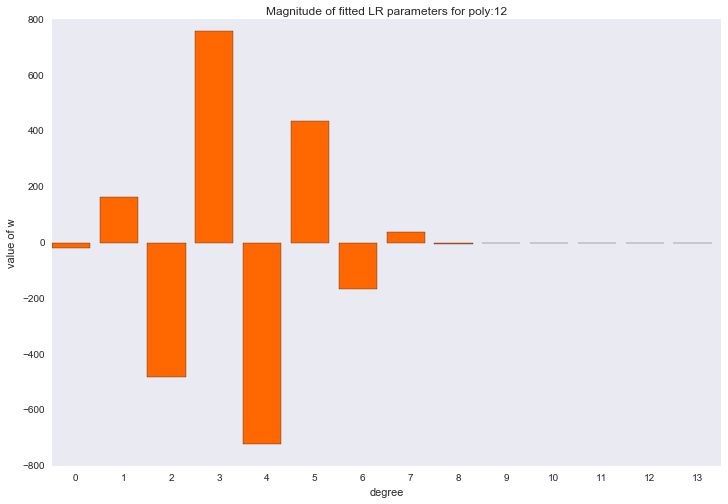
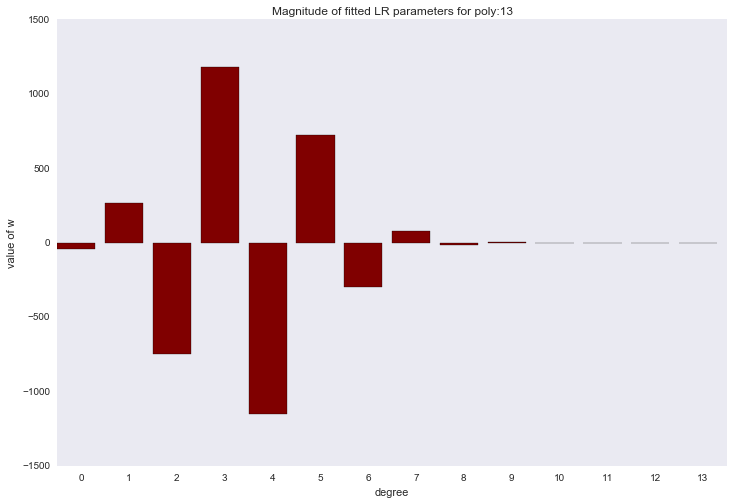
Перед тем как перейти к следующему разделу, давайте посмотрим на амплитуду параметров полиномиальной регрессии. Мы увидим, что при увеличении степени полинома, размах значений коэффициентов растет чуть ли не экспоненциально. Да, они еще и скачут в разные стороны.
Визуализация коэффициентов
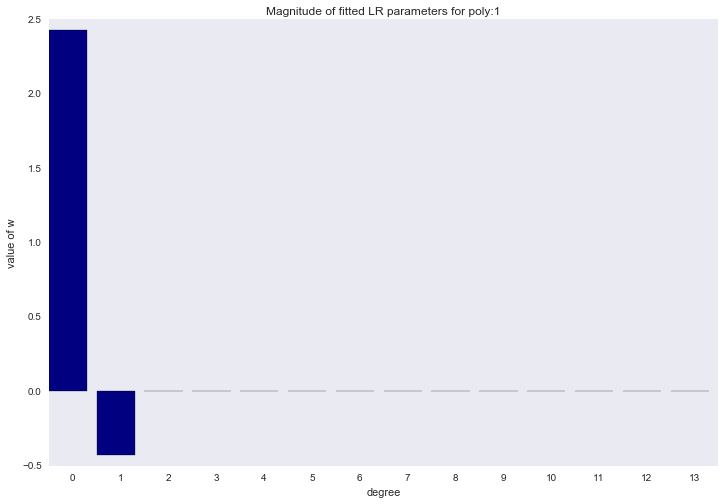
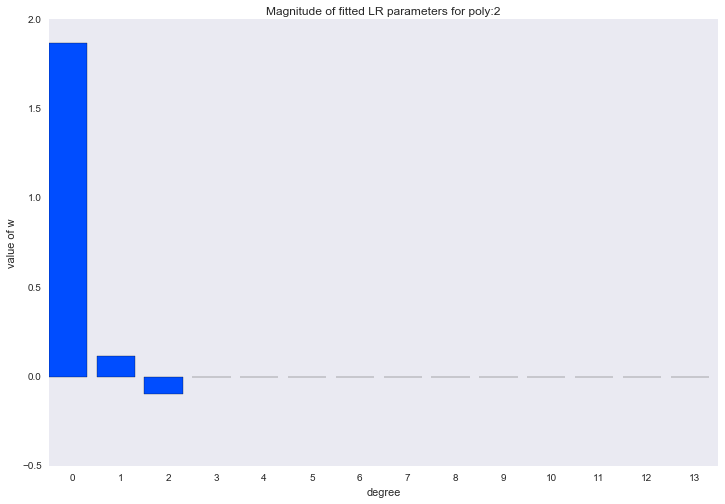
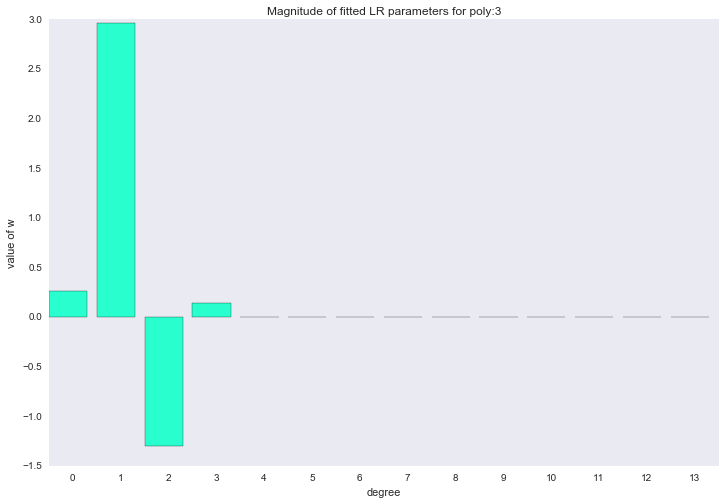
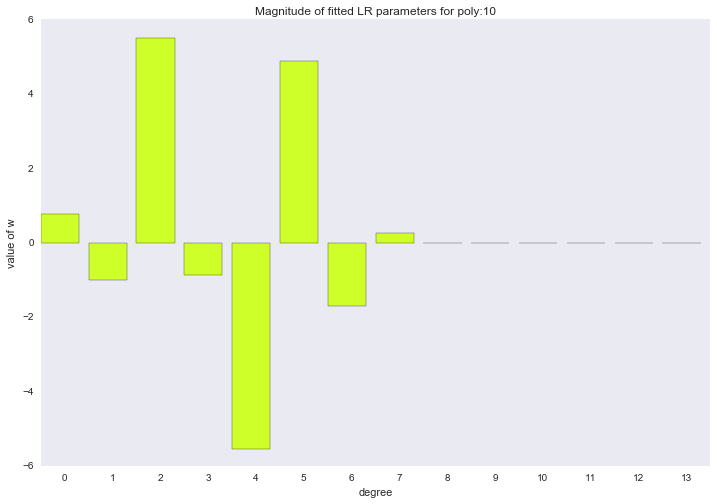
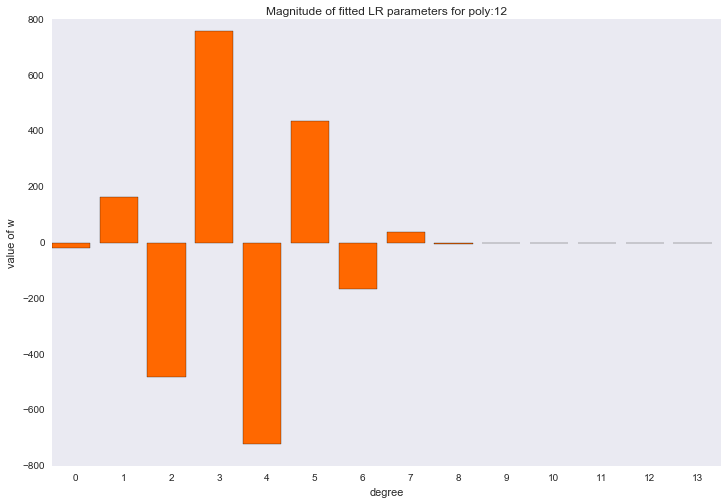
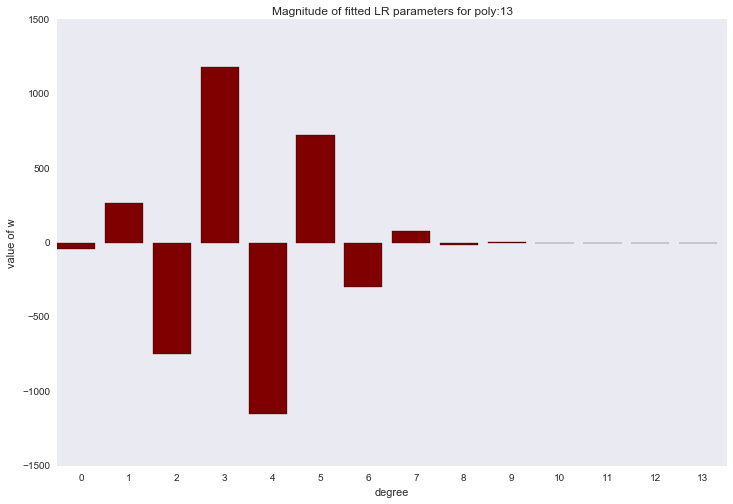
for ix, t in enumerate(w_list):
degree, w = t
fig, ax = plt.subplots()
plt.bar(range(max(degree_list) + 1), np.hstack((w, [0]*(max(degree_list) - w.shape[0] + 1))), color=colors[ix])
plt.title('Magnitude of fitted LR parameters for poly:%i' % degree)
plt.xlabel('degree')
plt.ylabel('value of w')
ax.set_xticks(np.array(range(max(degree_list) + 1)) + 0.5)
ax.set_xticklabels(range(max(degree_list) + 1))
plt.show()




 Регуляризация
Регуляризация
Регуляризация — это способ уменьшить сложность модели чтобы предотвратить переобучение или исправить некорректно поставленную задачу. Обычно это достигается добавлением некоторой априорной информации к условию задачи. Например так:
-
— это коэффициент регуляризации, то, насколько сильно мы хотим учитывать условие
На графиках мы увидели, что амплитуда значений коэффициентов слишком большая, попробуем ее уменьшить, добавив ограничение на
Новая функция стоимости примет вид:
Вычислим производную по параметрам:
И найдем решение в явном виде:
-
— единичная диагональна матрица
Такая регрессия называется гребневой регрессией (ridge regression). А гребнем является как раз диагональная матрица которую мы прибавляем к матрице

Для такой матрицы число обусловленности будет равно:
# define regularization parameter
lmbd = 0.1
degree_list = [1, 2, 3, 10, 12, 13]
cmap = plt.get_cmap('jet')
colors = [cmap(i) for i in np.linspace(0, 1, len(degree_list))]
margin = 0.3
plt.plot(data['support'], data['values'], 'b--', alpha=0.5, label='manifold')
plt.scatter(data['x_train'], data['y_train'], 40, 'g', 'o', alpha=0.8, label='data')
w_list_l2 = []
err = []
for ix, degree in enumerate(degree_list):
dlist = [[1]*data['x_train'].shape[0]] + map(lambda n: data['x_train']**n, range(1, degree + 1))
X = np.array(dlist).T
w = np.dot(np.dot(np.linalg.inv(np.dot(X.T, X) + lmbd*np.eye(X.shape[1])), X.T), data['y_train'])
w_list_l2.append((degree, w))
y_hat = np.dot(w, X.T)
plt.plot(data['x_train'], y_hat, color=colors[ix], label='poly degree: %i' % degree)
err.append(np.mean((data['y_train'] - y_hat)**2))
Отрисовка графика
plt.xlim(data['x_train'].min() - margin, data['x_train'].max() + margin)
plt.ylim(data['y_train'].min() - margin, data['y_train'].max() + margin)
plt.legend(loc='upper right', prop={'size': 20})
plt.title('Fitted polynomial regressions with L2 reg')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

| p | error |
|---|---|
| 1 | 0.26748 |
| 2 | 0.22546 |
| 3 | 0.08803 |
| 10 | 0.05833 |
| 12 | 0.05585 |
| 13 | 0.05638 |
В результате даже 13-ая степень ведет себя так, как мы ожидаем. Графики немного сгладились, хотя мы все равно наблюдаем небольшое переобучение на степенях выше третьей, что выражается в интерполяции данных в правой части графика.
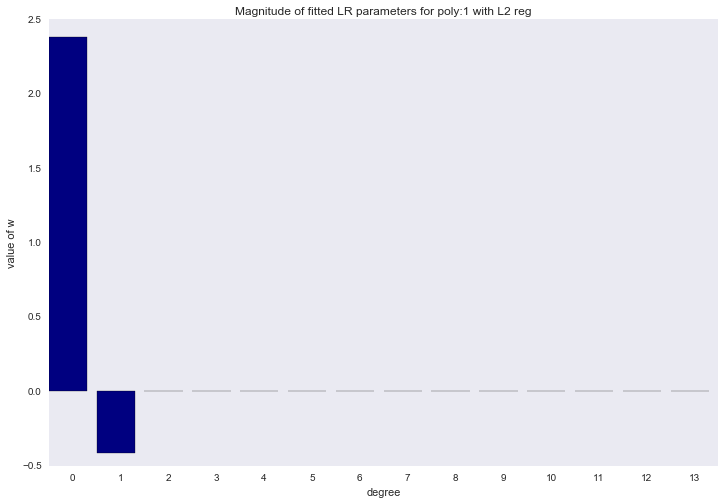
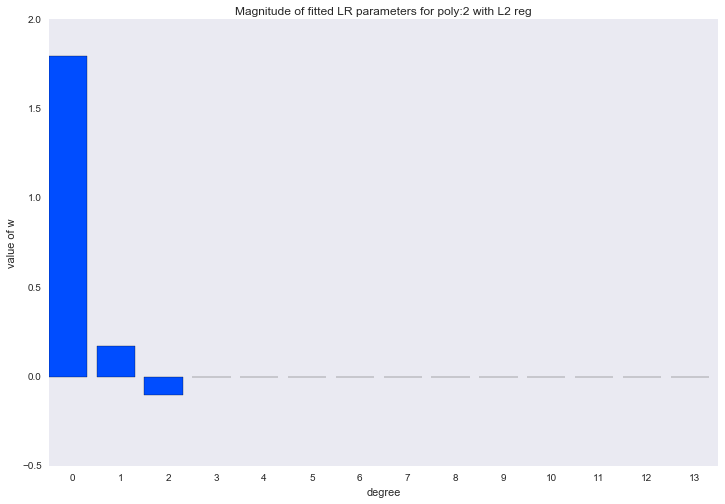
Визуализация коэффициентов
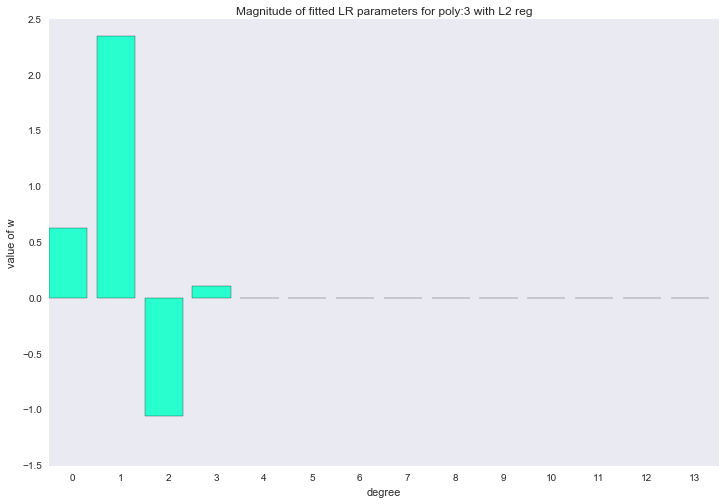
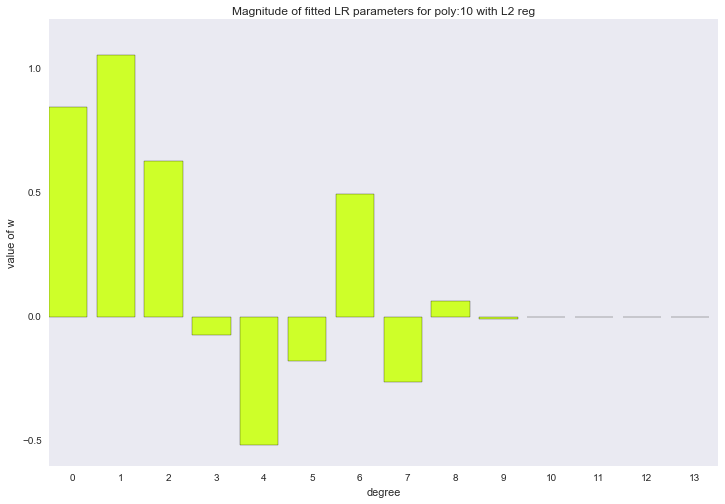
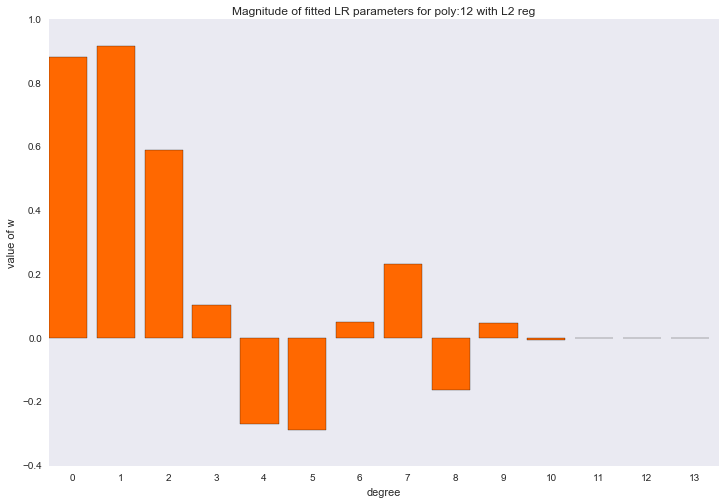
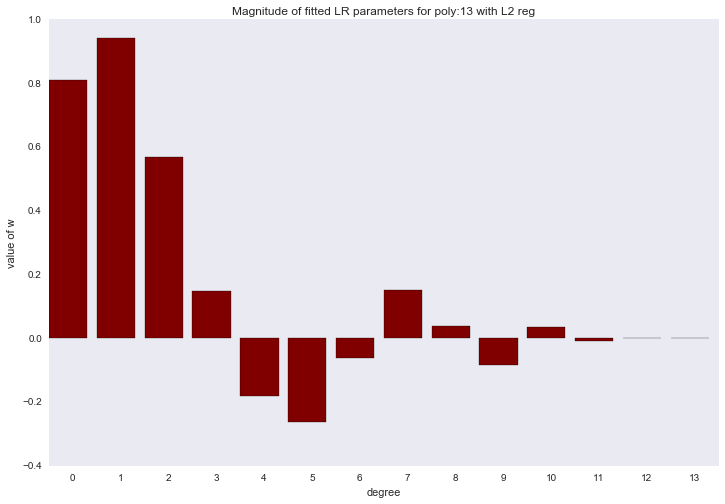
for ix, t in enumerate(w_list_l2):
degree, w = t
fig, ax = plt.subplots()
plt.bar(range(max(degree_list) + 1), np.hstack((w, [0]*(max(degree_list) - w.shape[0] + 1))), color=colors[ix])
plt.title('Magnitude of fitted LR parameters for poly:%i with L2 reg' % degree)
plt.xlabel('degree')
plt.ylabel('value of w')
ax.set_xticks(np.array(range(max(degree_list) + 1)) + 0.5)
ax.set_xticklabels(range(max(degree_list) + 1))
plt.show()

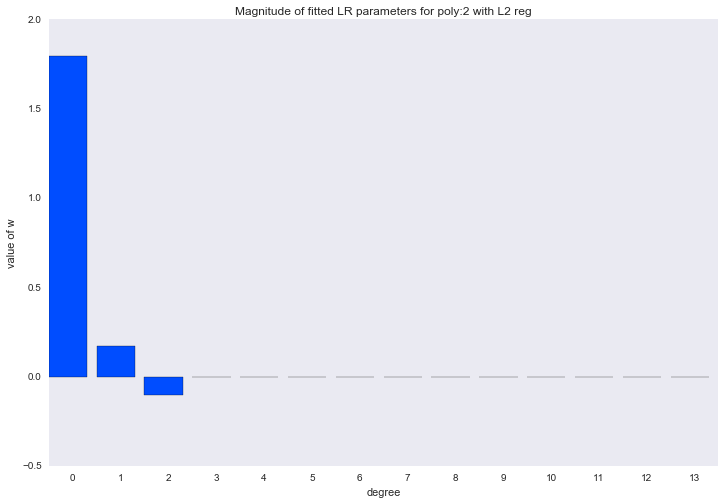



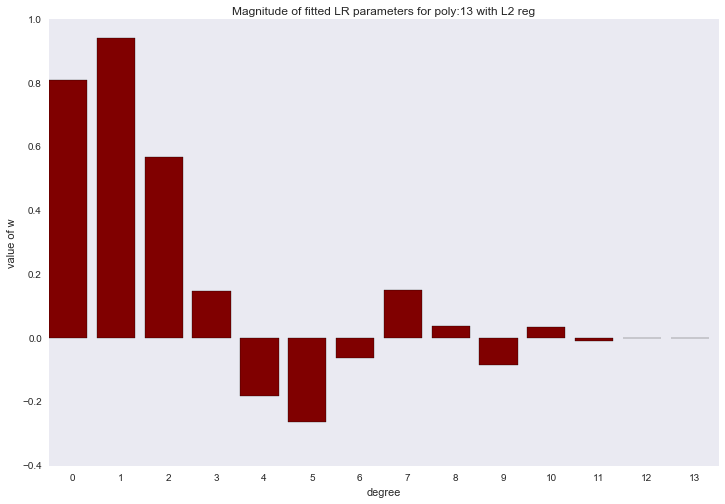
Амплитуда коэффициентов также изменилась, хотя скакать в разные стороны они не перестали. Мы помним, что полином третьей степени должен лучше всего описывать наши данные, хотелось бы, чтобы в результате регуляризации все коэффициенты при полиномиальных признаках степени выше третьей были равны нулю. И, оказывается, есть и такой регуляризатор.
 регуляризация
регуляризация
Попробуем теперь ограничить вектор параметров модели, используя
Тогда задача примет вид:
Посчитаем производную по параметрам модели (надеюсь уважаемые господа не будут пинать меня, за то, что я вжух и взял производную по модулю):
К сожалению, такая задача не имеет решения в явном виде. Для поиска хорошего приближенного решения мы воспользуемся методом градиентного спуска, тогда формула обновления весов примет вид:
а в задаче появляется еще один гиперпараметр
Запрограммировать такой алгоритм не составит труда, но нас ждет еще один сюрприз:
lmbd = 1
degree = 13
dlist = [[1]*data['x_train'].shape[0]] + map(lambda n: data['x_train']**n, range(1, degree + 1))
X = np.array(dlist).T
# функция для вычисления среднеквадратичное ошибки
def mse(u, v):
return ((u - v)**2).sum()/u.shape[0]
# начальное приближение
w = np.array([-1.0] * X.shape[1])
# максимальное количество итераций
n_iter = 20
# сделаем скорость обучения очень маленькой, на всякий случай
lr = 0.00000001
loss = []
for ix in range(n_iter):
w -= lr*(np.dot(np.dot(X, w) - data['y_train'], X)/X.shape[0] + lmbd*np.sign(w))
y_hat = np.dot(X, w)
loss.append(mse(data['y_train'], y_hat))
print loss[-1]
Получим такую вот эволюцию ошибки:
1.3051230958e+38
1.21979102398e+58
1.14003816725e+78
1.06549974318e+98
9.95834819687e+117
9.30724755635e+137
8.69871743413e+157
8.12997446782e+177
7.59841727794e+197
7.10161456943e+217
6.63729401109e+237
6.20333184222e+257
5.79774315864e+277
5.41867283397e+297
inf
inf
inf
inf
inf
inf
Даже при такой небольшой скорости обучения, ошибка все равно растет и очень даже стремительно. Причина в том, что каждый признак измеряется в разных масштабах, от небольших чисел у полиномиальных признаков 1-2 степени, до огромных при 12-13 степени. Для того чтобы итеративный процесс сошелся, необходимо либо выбрать экстремально мелкую скорость обучения, либо каким-то образом нормализовать признаки. Применим следующее преобразование к признакам и попробуем запустить процесс еще раз:
Такое преобразование называется стандартизацией, распределение каждого признака теперь имеет нулевое матожидание и единичную дисперсию.
lmbd = 1
degree = 13
dlist = [[1]*data['x_train'].shape[0]] + map(lambda n: data['x_train']**n, range(1, degree + 1))
X = np.array(dlist).T
# вычислим выборочное среднее каждого признака
x_mean = X.mean(axis=0)
# вычислим выборочное стандартное отклонение признаков
x_std = X.std(axis=0)
# применим преобразование
X = (X - x_mean)/x_std
X[:, 0] = 1.0
w = np.array([-1.0] * X.shape[1])
n_iter = 100
lr = 0.1
loss = []
for ix in range(n_iter):
w -= lr*(np.dot(np.dot(X, w) - data['y_train'], X)/X.shape[0] + lmbd*np.sign(w))
y_hat = np.dot(X, w)
loss.append(mse(data['y_train'], y_hat))
plt.plot(loss)
plt.title('Train error')
plt.xlabel('Iteration')
plt.ylabel('MSE')
plt.show()
Все стало сильно лучше.

Нарисуем теперь все графики:
degree_list = [1, 2, 3, 10, 12, 13]
cmap = plt.get_cmap('jet')
colors = [cmap(i) for i in np.linspace(0, 1, len(degree_list))]
margin = 0.3
plt.plot(data['support'], data['values'], 'b--', alpha=0.5, label='manifold')
plt.scatter(data['x_train'], data['y_train'], 40, 'g', 'o', alpha=0.8, label='data')
def mse(u, v):
return ((u - v)**2).sum()/u.shape[0]
def fit_lr_l1(X, y, lmbd, n_iter=100, lr=0.1):
w = np.array([-1.0] * X.shape[1])
loss = []
for ix_iter in range(n_iter):
w -= lr*(np.dot(np.dot(X, w) - y, X)/X.shape[0] +lmbd*np.sign(w))
y_hat = np.dot(X, w)
loss.append(mse(y, y_hat))
return w, y_hat, loss
w_list_l1 = []
for ix, degree in enumerate(degree_list):
dlist = [[1]*data['x_train'].shape[0]] + map(lambda n: data['x_train']**n, range(1, degree + 1))
X = np.array(dlist).T
x_mean = X.mean(axis=0)
x_std = X.std(axis=0)
X = (X - x_mean)/x_std
X[:, 0] = 1.0
w, y_hat, loss = fit_lr_l1(X, data['y_train'], lmbd=0.05)
w_list_l1.append((degree, w))
plt.plot(data['x_train'], y_hat, color=colors[ix], label='poly degree: %i' % degree)
Отрисовка графика
plt.xlim(data['x_train'].min() - margin, data['x_train'].max() + margin)
plt.ylim(data['y_train'].min() - margin, data['y_train'].max() + margin)
plt.legend(loc='upper right', prop={'size': 20})
plt.title('Fitted polynomial regressions with L1 reg')
plt.xlabel('x')
plt.ylabel('y')
plt.show()
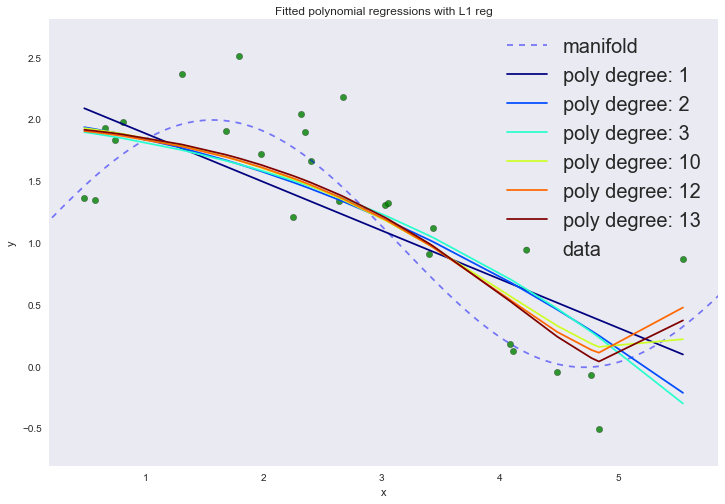
| p | error |
|---|---|
| 1 | 0.27204 |
| 2 | 0.23794 |
| 3 | 0.24118 |
| 10 | 0.18083 |
| 12 | 0.16069 |
| 13 | 0.15425 |
Если посмотреть на коэффициенты, мы увидим, что большая часть из них близка к нулю (то, что у 13-ой степени коэффициент совсем не нулевой, можно списать на шум и малое количество примеров в обучающей выборке; так же стоит помнить, что теперь все признаки измеряются в одинаковых шкалах).
Визуализация коэффициентов
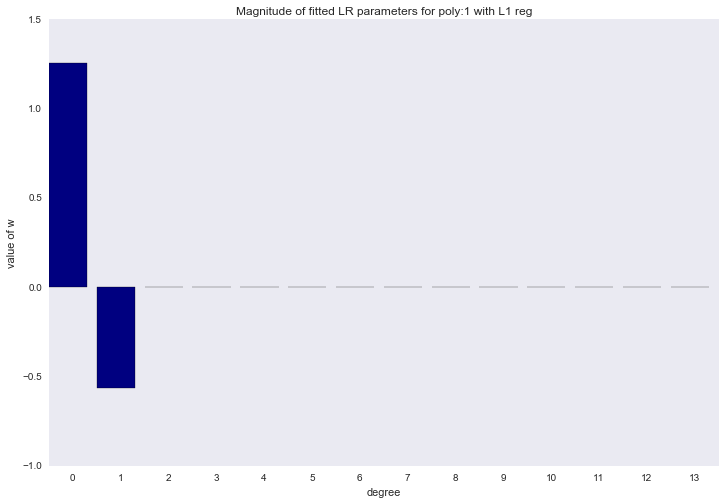
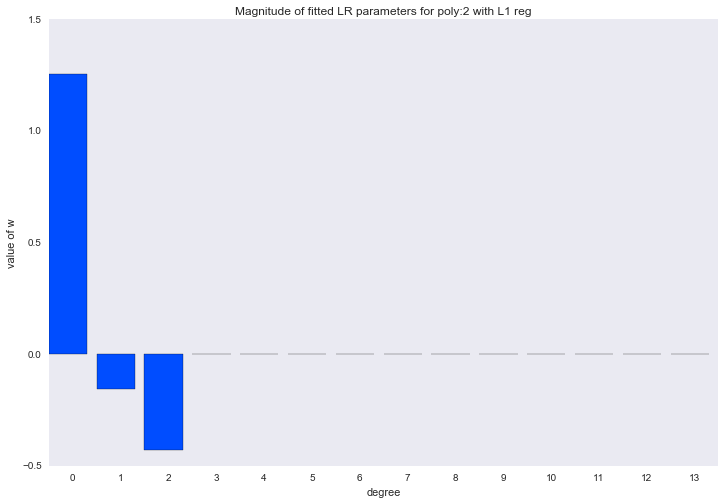
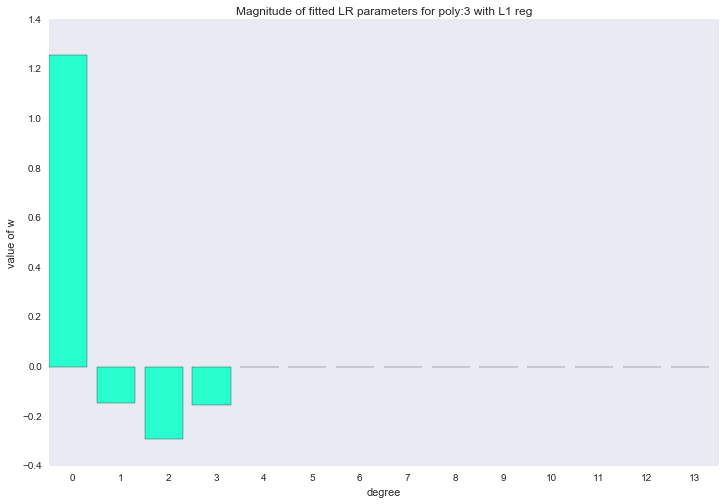
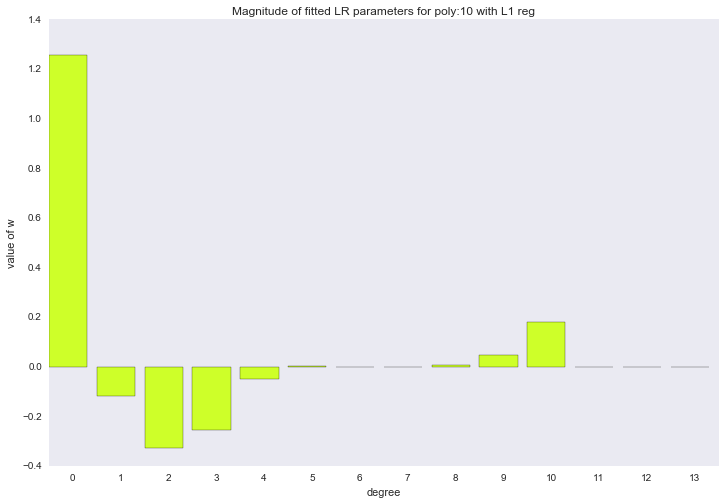
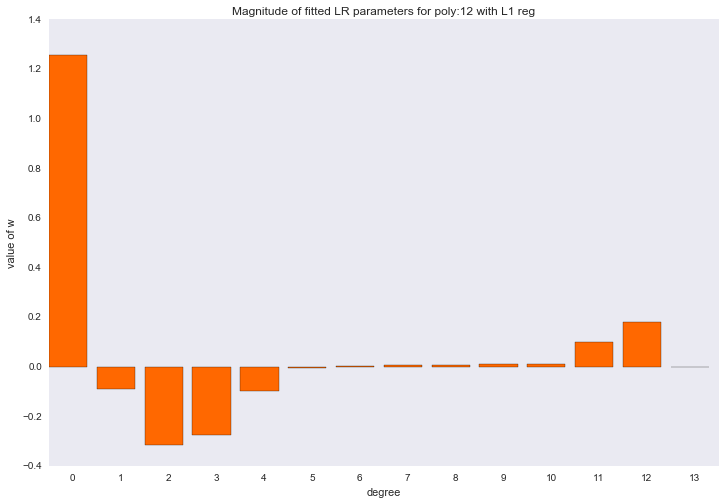
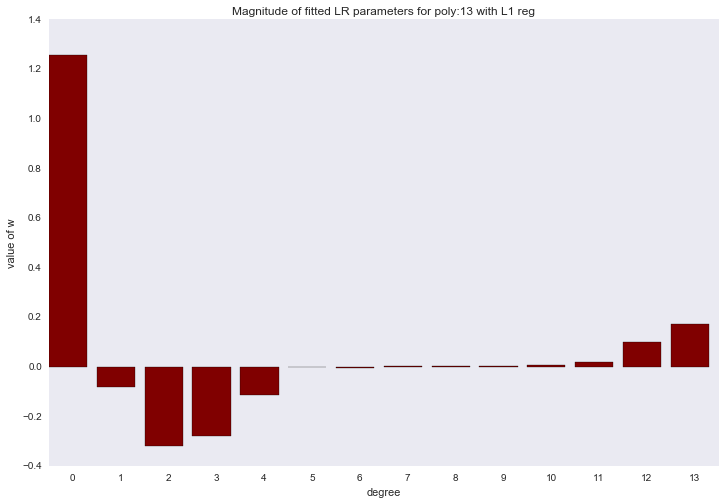
for ix, t in enumerate(w_list_l1):
degree, w = t
fig, ax = plt.subplots()
plt.bar(range(max(degree_list) + 1), np.hstack((w, [0]*(max(degree_list) - w.shape[0] + 1))), color=colors[ix])
plt.title('Magnitude of fitted LR parameters for poly:%i with L1 reg' % degree)
plt.xlabel('degree')
plt.ylabel('value of w')
ax.set_xticks(np.array(range(max(degree_list) + 1)) + 0.5)
ax.set_xticklabels(range(max(degree_list) + 1))
plt.show()


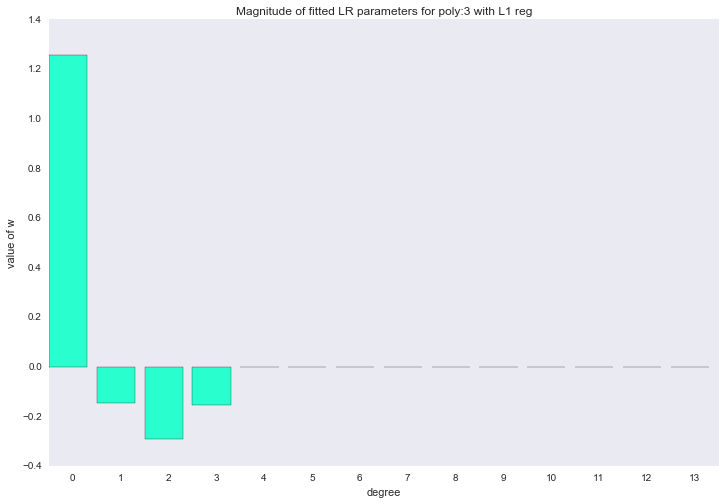
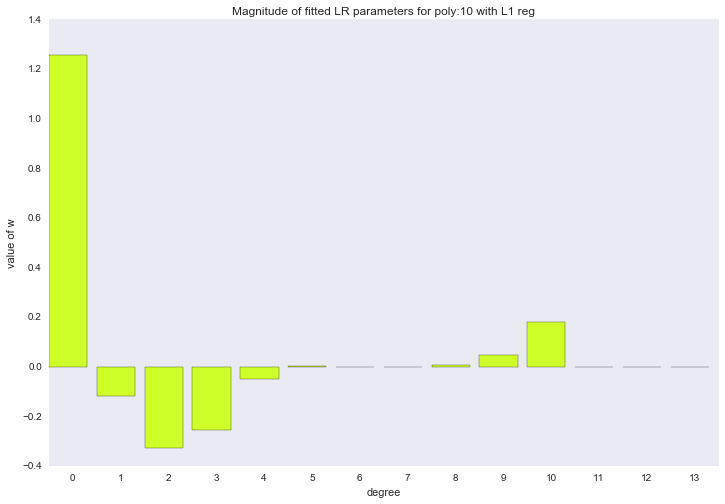


Описанный способ построения регрессии называется LASSO регрессия. Очень хотелось бы думать, что дядька на коне бросает веревку и ворует коэффициенты, а на их месте остается нуль. Но нет, LASSO = least absolute shrinkage and selection operator.
Байесовская интерпретация линейной регрессии
Две вышеописанные регуляризации, да и сама лининейная регрессия с квадратичной функцией ошибки, могут показаться какими-то грязными эмпирическими трюками. Но, оказывается, если взглянуть на эту модель с другой точки зрения, с точки зрения байесовой статистики, то все становится по местам. Грязные эмпирические трюки станут априорными предположениями. В основе байесовой статистики находится формула Байеса:
-
— априорные ожидания (prior): насколько правдоподобна гипотеза перед наблюдением данных;
-
— правдоподобие (likelihood): насколько правдоподобны данные при условии того, что гипотеза верна;
-
— маргинальная вероятность (marginal probability или evidence): вероятность данных, усредненная по всевозможным гипотезам;
-
— апостериорное распределение (posterior): насколько правдоподобна гипотеза при наблюдаемых данных.
В статистике обычно ищут точечную оценку максимума правдоподобия (ML = maximum likelihood):
В то время как в байесовом подходе интересуются апостериорным распределением:
Часто получается так, что интеграл, полученный в результате байесового вывода, крайне нетривиален (в случае линейной регрессии это, к счастью, не так), и тогда нужна точечная оценка. Тогда мы интересуемся максимумом апостериорного распределения (MAP = maximum a posteriori):
Давайте сравним ML и MAP гипотезы для линейной регрессии, это даст нам четкое понимание смысла регуляризаций. Будем считать, что все объекты из обучающей выборки были взяты из общей популяции независимо и равномерно распределенно. Это позволит нам записать совместную вероятность данных (правдоподобие) в виде:
А также будем считать, что целевая переменная подчиняется следующему закону:
или
Т.е. верное значение целевой переменной складывается из значения детерминированной линейной функции и некоторой непрогнозируемой случайной ошибки, с нулевым матожиданием и некоторой дисперсией. Тогда, мы можем записать правдоподобие данных как:
удобнее будет прологарифмировать это выражение:
И внезапно мы увидим, что оценка, полученная методом максимального правдоподобия, – это то же самое, что и оценка, полученная методом наименьших квадратов. Сгенерируем новый набор данных большего размера, найдем ML решение и визуализируем его.
data = generate_wave_set(1000, 100)
X = np.vstack((np.ones(data['x_train'].shape[0]), data['x_train'])).T
w = np.dot(np.dot(np.linalg.inv(np.dot(X.T, X)), X.T), data['y_train'])
Отрисовка графика
w0_support = np.linspace(-3, 3, 1000)
w1_support = np.linspace(-3, 3, 1000)
# create cartesian product of parameters
wx_space = list(it.product(w0_support, w1_support))
w0, w1 = zip(*wx_space)
# calculate MSE on dataset for each pairs of parameters
y = ((data['y_train'][:, np.newaxis] - np.dot(X, np.array(wx_space).T))**2).mean(axis=0)
plt.hexbin(w0, w1, C=y**(0.2), cmap=cm.jet_r, bins=None)
plt.axvline(0, color='black', linestyle='-', label='origin')
plt.axhline(0, color='black', linestyle='-')
plt.axvline(w[0], color='w', linestyle='--', label='ML solution')
plt.axhline(w[1], color='w', linestyle='--')
plt.axes().set_aspect('equal', 'datalim')
plt.title('ML solution')
plt.xlabel('w_0')
plt.ylabel('w_1')
plt.legend(loc='upper left', prop={'size': 20})
plt.show()

По оси абсцисс и ординат отложены различные значения всех двух параметров модели (решаем именно линейную регрессию, а не полиномиальную), цвет фона пропорционален значению правдоподобия в соответствующей точке значений параметров. ML решение находится на самом пике, где правдоподобие максимально.
Найдем MAP оценку параметров линейной регрессии, для этого придется задать какое-нибудь априорное распределение на параметры модели. Пусть для начала это будет опять нормальное распределение:
Нормальное распределение
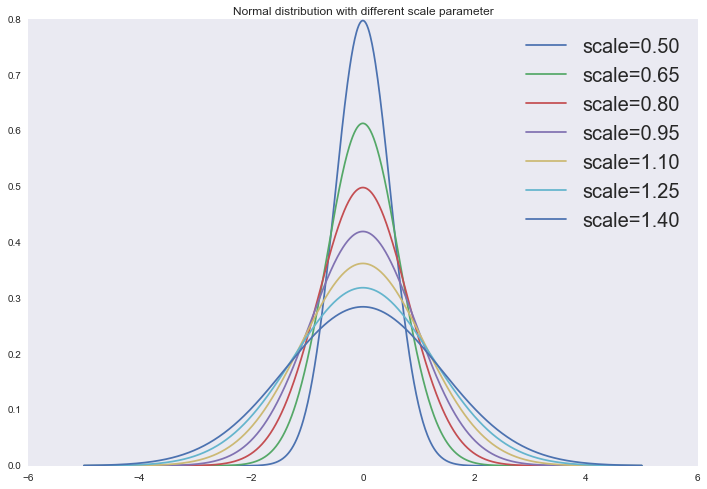
x = np.linspace(-5, 5, 1000)
for scale in np.linspace(0.5, 1.4, 7):
plt.plot(x, norm.pdf(x, scale=scale), label='scale=%0.2f' % scale)
plt.legend(loc='upper right', prop={'size': 20})
plt.title('Normal distribution with different scale parameter')
plt.show()

Тогда апостериорное распределение примет вид:
Если расписать логарифм этого выражения, то вы легко увидите, что добавление нормального априорного распределения — это то же самое, что и добавление
Отрисовка графика
w = np.dot(np.dot(np.linalg.inv(np.dot(X.T, X)), X.T), data['y_train'])
# solve L2 problems for different values of
w_l2 = {}
lmbd_space = np.linspace(0.5, 1500, 500)
for lmbd in lmbd_space:
w_l2[lmbd] = np.dot(np.dot(np.linalg.inv(np.dot(X.T, X) + lmbd*np.eye(X.shape[1])), X.T), data['y_train'])
w0_support = np.linspace(-3, 3, 1000)
w1_support = np.linspace(-3, 3, 1000)
wx_space = list(it.product(w0_support, w1_support))
w0, w1 = zip(*wx_space)
y = ((data['y_train'][:, np.newaxis] - np.dot(X, np.array(wx_space).T))**2).mean(axis=0)
plt.hexbin(w0, w1, C=y**(0.2), cmap=cm.jet_r, bins=None)
plt.axvline(0, color='black', linestyle='-', label='origin')
plt.axhline(0, color='black', linestyle='-')
# plot prior distribution of parameters
for i in range(1, 6):
plt.gcf().gca().add_artist(plt.Circle((0, 0), i*0.3, color='black', linestyle='--', alpha=0.1))
plt.axvline(w[0], color='w', linestyle='--', label='ML solution')
plt.axhline(w[1], color='w', linestyle='--')
# plot MAP solutions
flag = True
for _, w_l2_solution in w_l2.items():
plt.plot(w_l2_solution[0], w_l2_solution[1], color='c', marker='.', mew=1, alpha=0.5,
label='MAP L2 solution' if flag else None)
flag = False
plt.axes().set_aspect('equal', 'datalim')
plt.title('ML and MAP L2 for different values of lambda')
plt.xlabel('w_0')
plt.ylabel('w_1')
plt.legend(loc='upper left', prop={'size': 20})
plt.show()

Теперь на график добавились круги, исходящие от центра — это плотность априорного распределения (круги, а не эллипсы из-за того, что матрица ковариации данного нормального распределения диагональна, а на диагонали находится одно и то же число). Точками обозначены различные решения MAP задачи. При увеличении параметра регуляризации (что эквивалентно уменьшению дисперсии), мы заставляем решение отдаляться от ML оценки и приближаться к центру априорного распределения. При большом значении параметра регуляризации, все параметры будут близки к нулю.
Естественно мы можем наложить и другое априорное распределение на параметры модели, например распределение Лапласа, тогда получим то же самое, что и при
Распределение Лапласа
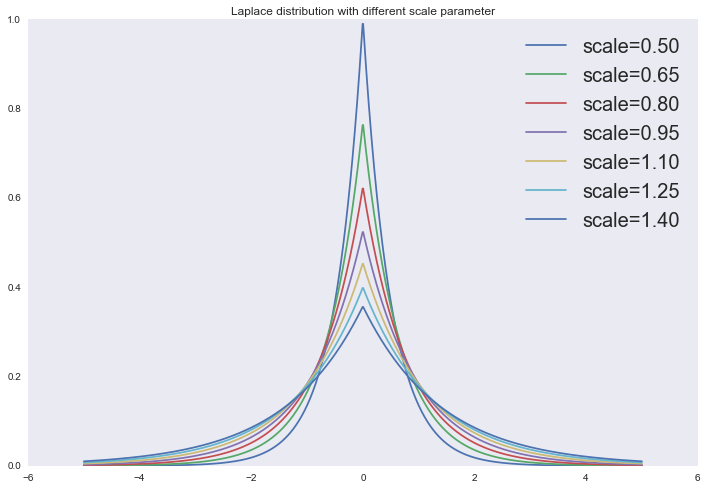
from scipy.stats import laplace
x = np.linspace(-5, 5, 1000)
for scale in np.linspace(0.5, 1.4, 7):
plt.plot(x, laplace.pdf(x, scale=scale), label='scale=%0.2f' % scale)
plt.legend(loc='upper right', prop={'size': 20})
plt.title('Laplace distribution with different scale parameter')
plt.show()

Тогда апостериорное распределение примет вид:
Отрисовка графика
w_l1 = {}
lmbd_space = np.linspace(0.001, 2, 200)
for lmbd in tqdm(lmbd_space):
w_l1[lmbd] = fit_lr_l1(X, data['y_train'], lmbd, n_iter=10000, lr=0.001)[0]
w0_support = np.linspace(-3, 3, 1000)
w1_support = np.linspace(-3, 3, 1000)
wx_space = list(it.product(w0_support, w1_support))
w0, w1 = zip(*wx_space)
y = ((data['y_train'][:, np.newaxis] - np.dot(X, np.array(wx_space).T))**2).mean(axis=0)
plt.hexbin(w0, w1, C=y**(0.2), cmap=cm.jet_r, bins=None)
plt.axvline(0, color='black', linestyle='-', label='origin')
plt.axhline(0, color='black', linestyle='-')
# function to plot rhomb
def plot_rhomb(cx=0, cy=0, r=0.5):
plt.gcf().gca().add_artist(plt.Rectangle((cx, cy - np.sqrt(2*r**2)), 2*r, 2*r, angle=45,
color='black', linestyle='--', alpha=0.1))
# plot Laplace distribution density
for i in range(1, 6):
plot_rhomb(r=0.2*i)
plt.axvline(w[0], color='w', linestyle='--', label='ML solution')
plt.axhline(w[1], color='w', linestyle='--')
# plot MAP solutions
flag = True
for _, w_l1_solution in w_l1.items():
plt.plot(w_l1_solution[0], w_l1_solution[1], color='c', marker='.', mew=1, alpha=0.5,
label='MAP L1 solution' if flag else None)
flag = False
plt.axes().set_aspect('equal', 'datalim')
plt.title('ML and MAP L1 for different values of lambda')
plt.xlabel('w_0')
plt.ylabel('w_1')
plt.legend(loc='upper left', prop={'size': 20})
plt.show()

Глобальная динамика не изменилась: увеличиваем параметр регуляризации — решение приближается к центру априорного распределения. Также мы можем наблюдать, что такая регуляризация способствует нахождению разреженных решений: вы можете видеть два участка, на которых сначала один параметр равен нулю, затем второй параметр (в конце оба равны нулю).
И на самом деле два описанных регуляризатора — это частные случаи наложения обобщенного нормального распределения в качестве априорного распределения на параметры линейной регрессии:
Отрисовка графика
from scipy.stats import gennorm
x = np.linspace(-5, 5, 1000)
for beta in np.linspace(0, 3, 11):
plt.plot(x, gennorm.pdf(x, beta=beta), label='beta=%0.2f' % beta)
plt.legend(loc='upper right', prop={'size': 20})
plt.title('Generalized normal distribution with different beta parameter')
plt.show()
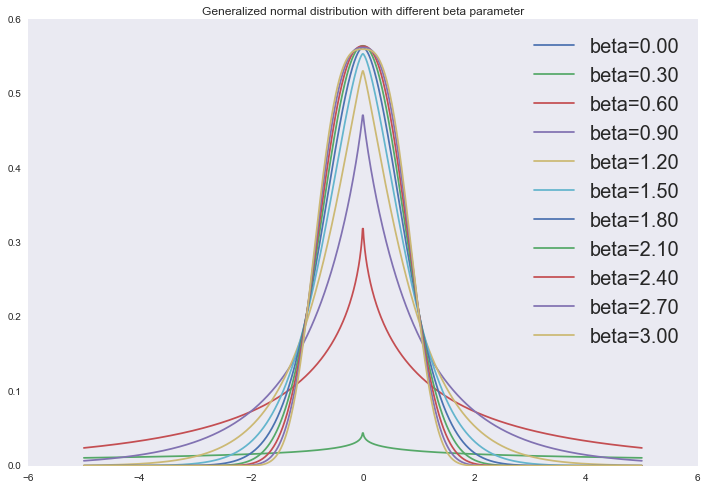
Или же мы можем смотреть на эти регуляризаторы с точки зрения ограничения
Отрисовка графика
f, ax = plt.subplots(3, 4)
ax = reduce(lambda a, b: a + b, ax.tolist())
a_list = np.linspace(0, 2*np.pi, 361)
r_list = np.linspace(0, 1.1, 100)
for ix, p in enumerate(np.linspace(0.25, 3, 12)):
points = []
for a in a_list:
r_inner = []
for r in r_list:
if np.linalg.norm([r*np.cos(a), r*np.sin(a)], p) > 1:
break
r_inner.append(r)
r = max(r_inner)
points.append([r*np.cos(a), r*np.sin(a)])
points = np.array(points)
ax[ix].plot(points[:, 0], points[:, 1])
ax[ix].set_aspect('equal', 'datalim')
ax[ix].set_title('Circle in Lp space, p=%0.2f' % p)
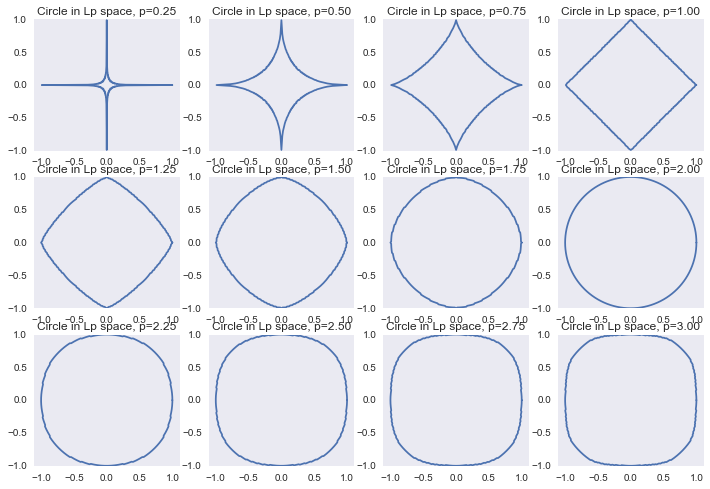
Заключение
Здесь вы найдете jupyter notebook со всем вышеописанным и несколькими бонусами. Отдельное спасибо тем, кто осилил этот текст до конца.
Желающим копнуть эту тему глубже, рекомендую:
- лекции Сергея Николенко, откуда позаимствована идея этого jupyter notebook'a;
- лекции Бориса Демешева по эконометрике (со 146ого видео), и его же курс на курсере.
Понимание линейной регрессии является ключом к пониманию более сложных моделей, вплоть до глубоких нейронных сетей. Если мы возьмем сигмойд от линейной функции — получим логистическую регрессию. Состекаем несколько логрегрессоров в один слой — получим softmax regression/max entropy regression. А если состекать несколько слоев — будет неронная сеть. Такие дела.
Вступайте в ods.ai, приходите на наши сходки, we will make ML great again!
