Постоянно падающая популярность предыдущих публикаций побуждает предпринимать поступки, помогающие популярность поддержать. Приметил – популярность первых публикаций порядочно превышает последующие; поэтому попробую перезагрузиться.
На протяжении предыдущих серий мы тщательно рассмотрели метод SVD и даже довели его до программного кода; начиная с этого текста, я буду рассматривать более общие вещи. Вещи эти, конечно, всегда будут тесно связаны с рекомендательными системами, и я буду рассказывать о том, как они в рекомендательных системах возникают, но постараюсь делать упор на более общих концепциях машинного обучения. Сегодня – об оверфиттинге и регуляризации.

Начну с классического, но от этого не менее показательного примера. Давайте откроем R (если кто не знает, R – это один из лучших в мире инструментов для всевозможной статистики, машинного обучения и вообще обработки данных; очень рекомендую) и сгенерируем себе какой-нибудь маленький простенький датасет. Я возьму простой кубический многочлен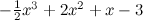 и добавлю к его точкам нормально распределённый шум.
и добавлю к его точкам нормально распределённый шум.
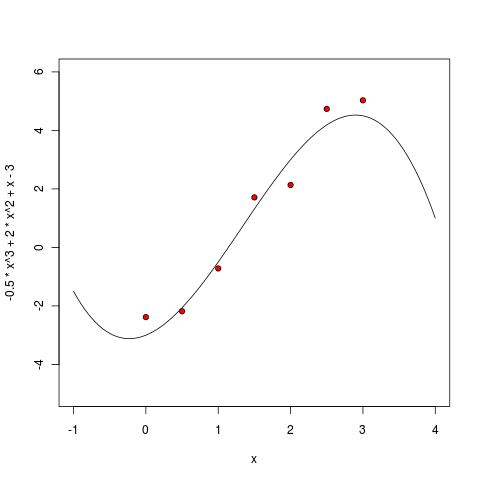
Эти точки теперь можно нарисовать вместе с идеальной кривой.
Получится как на рисунке:
А теперь давайте попробуем обучить многочлен по этим данным. Мы будем минимизировать сумму квадратов отклонений точек от многочлена (будем делать самую обычную классическую регрессию), то есть будем искать такой многочлен p(x), который минимизирует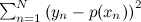 .
.
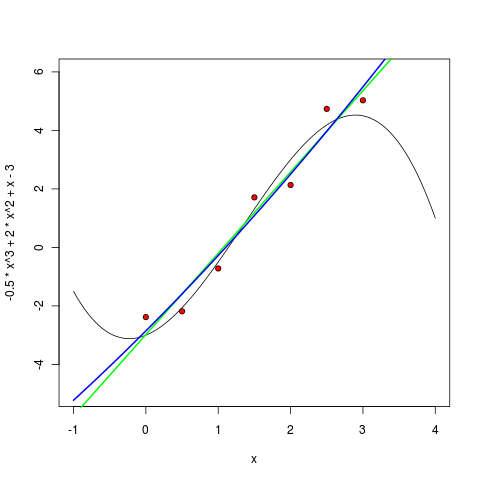
Разумеется, в R это делается одной командой. Сначала обучим и нарисуем линейный многочлен:
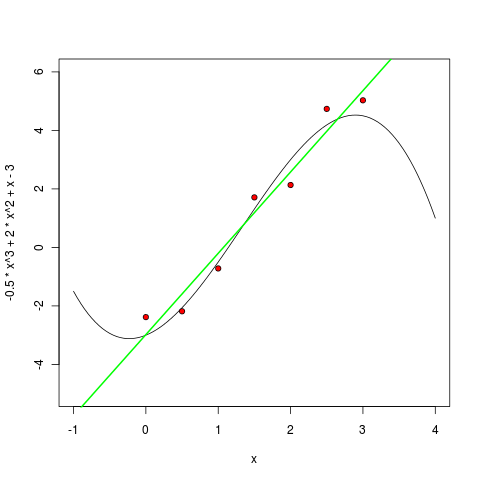
Потом многочлен второй степени:
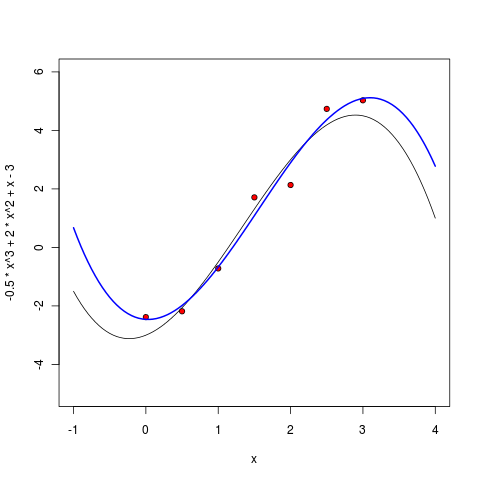
Многочлен третьей степени, как и ожидалось, уже вполне себе похож:
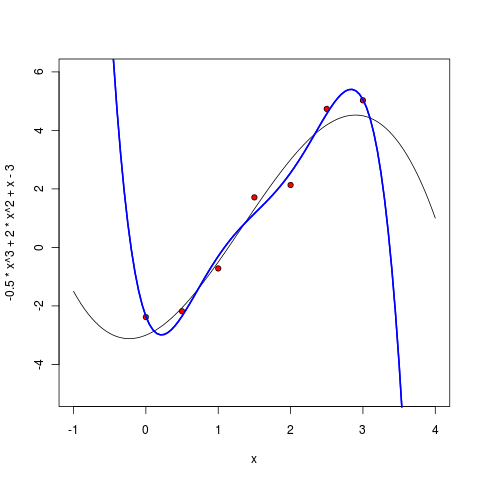
Но что произойдёт, если увеличивать степень дальше? На практике ведь мы, скорее всего, не будем знать «истинной степени многочлена», т.е. истинной сложности модели. Может показаться, что мы будем, усложняя модель, всё лучше приближать имеющиеся точки, и результаты будут всё лучше и лучше, просто обучить модель будет всё сложнее и сложнее. Посмотрим, так ли это на самом деле.
Уже многочлен пятой степени выглядит весьма подозрительно – он, конечно, всё ещё хорошо себя ведёт между точками, но уже видно, что экстраполировать по этой модели будет нехорошо – слишком резко он начинает уходить на бесконечность, как только точки заканчиваются.
Начиная с шестой степени, мы видим уже несомненный epic fail нашего подхода. Ошибка, которую мы хотели минимизировать, теперь строго равна нулю – ведь через семь точек можно точно провести многочлен шестой степени! Но вот польза от получившейся модели тоже, пожалуй, строго равна нулю – многочлен теперь не только плохо экстраполирует за пределы имеющихся точек, но даже интерполирует между ними чрезвычайно странно, далеко убегая на локальные экстремумы там, где этого из точек трудно ожидать.
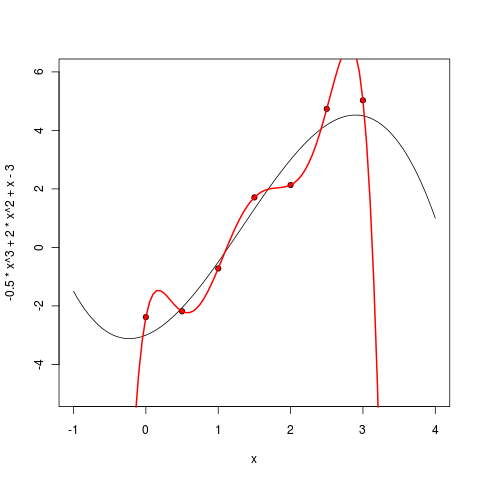
Что же произошло? Произошло то, что в машинном обучении называется словом оверфиттинг (overfitting): мы взяли модель, в которой было слишком много параметров, и модель слишком хорошо обучилась по данным, а главное – предсказательная сила – от этого, наоборот, пострадала.
Что же делать? Я в следующих сериях расскажу, как это может получиться более концептуально, а сейчас давайте просто примем на веру: оверфиттинг в данном случае проявляется в том, что в получающихся многочленах слишком большие коэффициенты. Например, вот многочлен третьей степени, который мы обучили:
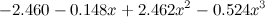 ,
,
а вот – почувствуйте разницу – шестой степени:
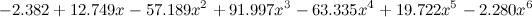 .
.
Соответственно, и бороться с этим можно довольно естественным способом: нужно просто добавить в целевую функцию штраф, который бы наказывал модель за слишком большие коэффициенты:
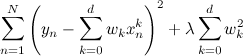 .
.
Именно такой оверфиттинг сплошь и рядом происходил бы в SVD, если бы мы позволили ему происходить. Действительно, мы вводим на каждого пользователя и каждый продукт число свободных параметров, равное числу факторов (т.е. минимум несколько, а может быть, и несколько десятков). Поэтому SVD без регуляризации совершенно неприменимо – обучится, конечно, хорошо, но для предсказаний, скорее всего, будет практически бесполезно.
Регуляризаторы в SVD работают точно так же, как в обычной регрессии – мы добавляем штраф, который тем больше, чем больше размеры коэффициентов; в одной из предыдущих серий я сразу с регуляризаторами и выписывал целевую функцию:
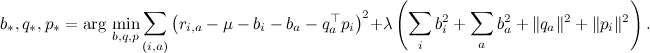
Формулы градиентного подъёма приведены там же – за регуляризацию в них отвечает коэффициент λ.
Однако пока это всё выглядит довольно загадочно – с какой стати вдруг большие коэффициенты хуже маленьких? В дальнейшем я буду рассказывать о том, как можно смотреть на этот вопрос с более концептуальной байесовской стороны.
На протяжении предыдущих серий мы тщательно рассмотрели метод SVD и даже довели его до программного кода; начиная с этого текста, я буду рассматривать более общие вещи. Вещи эти, конечно, всегда будут тесно связаны с рекомендательными системами, и я буду рассказывать о том, как они в рекомендательных системах возникают, но постараюсь делать упор на более общих концепциях машинного обучения. Сегодня – об оверфиттинге и регуляризации.

Начну с классического, но от этого не менее показательного примера. Давайте откроем R (если кто не знает, R – это один из лучших в мире инструментов для всевозможной статистики, машинного обучения и вообще обработки данных; очень рекомендую) и сгенерируем себе какой-нибудь маленький простенький датасет. Я возьму простой кубический многочлен
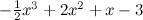 и добавлю к его точкам нормально распределённый шум.
и добавлю к его точкам нормально распределённый шум.> x <- c(0:6) / 2
> y_true <- -.5*x^3 + 2*x^2 + x – 3
> err <- rnorm( 7, mean=0, sd=0.4 )
> y <- y_true + err
> y
[1] -2.3824664 -2.1832300 -0.7187618 1.7105423 2.1338531 4.7356023 5.0291615
Эти точки теперь можно нарисовать вместе с идеальной кривой.
> curve(-.5*x^3 + 2*x^2 + x - 3, -1, 4, ylim=c(-5,6) )
> points(x, y, pch=21, bg="red")
Получится как на рисунке:

А теперь давайте попробуем обучить многочлен по этим данным. Мы будем минимизировать сумму квадратов отклонений точек от многочлена (будем делать самую обычную классическую регрессию), то есть будем искать такой многочлен p(x), который минимизирует
 .
.Разумеется, в R это делается одной командой. Сначала обучим и нарисуем линейный многочлен:
> m1 <- lm ( y ~ poly(x, 1, raw=TRUE) )
> pol1 <- function(x) m1$coefficients[1] + m1$coefficients[2] * x
> curve(pol1, col="green", lwd=2, add=TRUE)
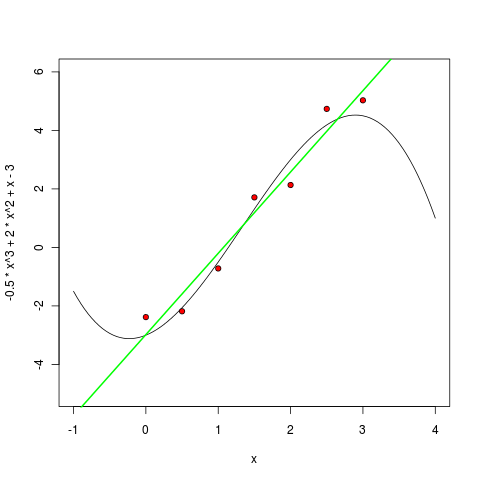
Потом многочлен второй степени:
> m2 <- lm ( y ~ poly(x, 2, raw=TRUE) )
> pol2 <- function(x) m2$coefficients[1] + m1$coefficients[2] * x + m1$coefficients[3] * (x^2)
> curve(pol2, col="blue", lwd=2, add=TRUE)
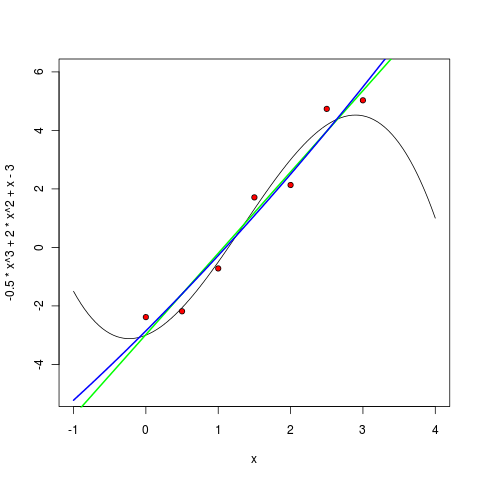
Многочлен третьей степени, как и ожидалось, уже вполне себе похож:

Но что произойдёт, если увеличивать степень дальше? На практике ведь мы, скорее всего, не будем знать «истинной степени многочлена», т.е. истинной сложности модели. Может показаться, что мы будем, усложняя модель, всё лучше приближать имеющиеся точки, и результаты будут всё лучше и лучше, просто обучить модель будет всё сложнее и сложнее. Посмотрим, так ли это на самом деле.
Уже многочлен пятой степени выглядит весьма подозрительно – он, конечно, всё ещё хорошо себя ведёт между точками, но уже видно, что экстраполировать по этой модели будет нехорошо – слишком резко он начинает уходить на бесконечность, как только точки заканчиваются.
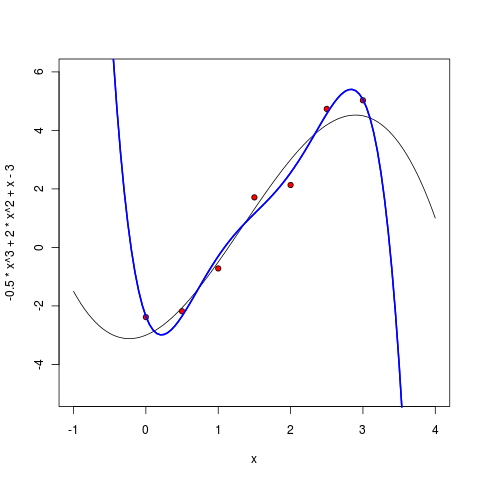
Начиная с шестой степени, мы видим уже несомненный epic fail нашего подхода. Ошибка, которую мы хотели минимизировать, теперь строго равна нулю – ведь через семь точек можно точно провести многочлен шестой степени! Но вот польза от получившейся модели тоже, пожалуй, строго равна нулю – многочлен теперь не только плохо экстраполирует за пределы имеющихся точек, но даже интерполирует между ними чрезвычайно странно, далеко убегая на локальные экстремумы там, где этого из точек трудно ожидать.
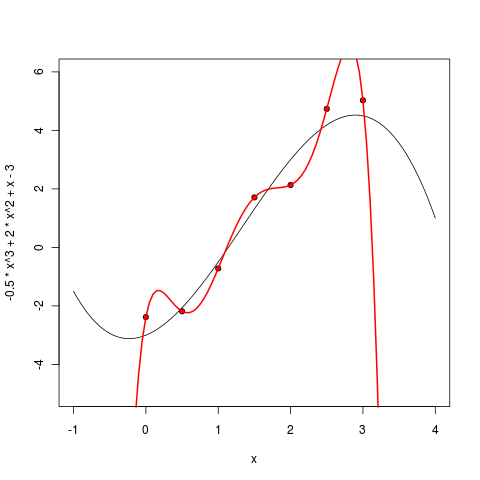
Что же произошло? Произошло то, что в машинном обучении называется словом оверфиттинг (overfitting): мы взяли модель, в которой было слишком много параметров, и модель слишком хорошо обучилась по данным, а главное – предсказательная сила – от этого, наоборот, пострадала.
Что же делать? Я в следующих сериях расскажу, как это может получиться более концептуально, а сейчас давайте просто примем на веру: оверфиттинг в данном случае проявляется в том, что в получающихся многочленах слишком большие коэффициенты. Например, вот многочлен третьей степени, который мы обучили:
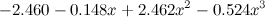 ,
,а вот – почувствуйте разницу – шестой степени:
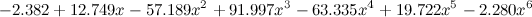 .
.Соответственно, и бороться с этим можно довольно естественным способом: нужно просто добавить в целевую функцию штраф, который бы наказывал модель за слишком большие коэффициенты:
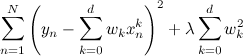 .
.Именно такой оверфиттинг сплошь и рядом происходил бы в SVD, если бы мы позволили ему происходить. Действительно, мы вводим на каждого пользователя и каждый продукт число свободных параметров, равное числу факторов (т.е. минимум несколько, а может быть, и несколько десятков). Поэтому SVD без регуляризации совершенно неприменимо – обучится, конечно, хорошо, но для предсказаний, скорее всего, будет практически бесполезно.
Регуляризаторы в SVD работают точно так же, как в обычной регрессии – мы добавляем штраф, который тем больше, чем больше размеры коэффициентов; в одной из предыдущих серий я сразу с регуляризаторами и выписывал целевую функцию:
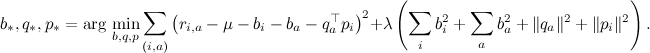
Формулы градиентного подъёма приведены там же – за регуляризацию в них отвечает коэффициент λ.
Однако пока это всё выглядит довольно загадочно – с какой стати вдруг большие коэффициенты хуже маленьких? В дальнейшем я буду рассказывать о том, как можно смотреть на этот вопрос с более концептуальной байесовской стороны.