Это первый пост из блога Surfingbird, который я выношу в общие хабы алгоритмов и искусственного интеллекта; честно говоря, раньше просто не догадался. Если интересно, заходите к нам, чтобы прочесть предыдущие тексты, – я не знаю, что произойдёт, если просто добавить новые хабы к постам несколькомесячной давности.
Краткое содержание предыдущих серий о рекомендательных системах:
В этот раз начинаем новую тему – о многоруких бандитах. Бандиты – это самая простая, но от этого только более важная постановка задачи в так называемом обучении с подкреплением…

Мы всё время говорим, что то, что мы делаем, – это машинное обучение (machine learning). Однако задумайтесь: как вы на самом деле обучаетесь? Неужели мы с вами строим регрессию движения пальцев на основе наблюдений за машинистками для того, чтобы научиться слепой печати? Неужели ребёнок, чтобы научиться ходить, сначала собирает и обобщает коллекцию примеров прямохождения родителей? На самом деле, конечно, нет: в таких случаях мы просто пробуем что-нибудь сделать, смотрим, получилось ли, а затем пытаемся (обычно бессознательно) скорректировать своё поведение на основе полученного результата.
Такая постановка задачи называется обучением с подкреплением: есть агент, который действует в какой-то среде; агент пытается что-то делать, а среда в ответ на его действия выдаёт агенту плюшки или, наоборот, бьёт током. Агент старается получить плюшек побольше, а током – пореже. В общем, типичная мышка в лабиринте.
Сегодня, однако, мы поговорим о мышке, которая попала даже не в лабиринт, а в самый обычный skinner box – давайте предположим, что состояние среды/агента от действия к действию не изменяется. Иначе говоря, у агента есть некоторый набор возможных действий, агент выбирает одно из них, получает за это некоторое вознаграждение (которое является случайной величиной), а затем снова может выбирать из тех же действий. В машинном обучении такая постановка задачи получила название многоруких бандитов (multiarmed bandits): вы сидите в комнате перед несколькими игровыми автоматами и должны постараться выиграть как можно больше.
(картинка с сайта Microsoft Research)
Зачем это нужно в реальной жизни? К примеру, представьте себе, что вы – Yahoo! или, скажем, mail.ru. У вас есть домашняя страница, на которой бывают миллионы людей каждый день. Вы хотите размещать на ней ссылки так, чтобы на них кликали как можно чаще. Как выбрать те ссылки, которые дают максимальный CTR (click-through ratio)? Здесь каждый показ ссылки пользователю соответствует «дёрганию за ручку»; каждый клик – успех, положительное подкрепление от среды; не-клик – неудача. Задача алгоритма будет в том, чтобы как можно быстрее понять, что та или иная новость «горяча», и начать её показывать (да, это чуть модифицированная задача, в которой бандиты время от времени умирают и рождаются вновь).
Другой пример: представьте себе, что вы хотите протестировать какой-то набор изменений в интерфейсе своего сайта. Обычно это делается при помощи так называемого A/B testing – вы должны выбрать группу для эксперимента (по каждому изменению в отдельности), контрольную группу, для которой ничего не изменится, затем собрать статистику и оценить, значимо ли улучшение. Однако такая схема сама по себе не отвечает на главный вопрос – как долго надо собирать статистику? Здесь бандиты тоже могут придти на помощь, постановка задачи ведь в точности бандитская: показ того или иного варианта соответствует дёрганию за ручку, а действия пользователя определяют ответ окружающей среды (см., например, вот этот пост).
Однако вернёмся к постановке задачи. На первый взгляд кажется, что задача выбрать оптимальную ручку очень простая: нужно дёрнуть за каждую ручку по тысяче раз, а потом выбрать ручку с наибольшим средним. И действительно, такой алгоритм, скорее всего, сделает правильный выбор – но сколько он потеряет «денег» на субоптимальных ручках! Многих из этих потерь можно было бы избежать. Вообще, лучшая метрика для оценки качества «бандитского» алгоритма – это его потери (regret) по сравнению с оптимальным алгоритмом, т.е. ожидание разности дохода от стратегии «всегда дёргать за оптимальную ручку» и рассматриваемой стратегии.
В качестве примера я сразу приведу алгоритм с одними из самых лучших гарантий на эту самую меру потерь на обучение. Это алгоритм UCB1; сам алгоритм очень простой, доказательство его оптимальности, конечно, не такое простое, но в это мы углубляться не будем, а интересующихся я отсылаю к статье [Auer et al., 2002]; там же можно найти и более «продвинутую» версию с улучшенными константами.
Хотя формальное доказательство того, что здесь должно быть именно два натуральных логарифма, а не что-то другое, выходит за пределы этой статьи, интуитивно совершенно понятно, что происходит в этом алгоритме: мы придумали эвристику, оценку приоритета, по которой мы выбираем, за какую ручку дёргать. Логично, что этот приоритет тем больше, чем больше средний доход, но не только: бонус также получают те ручки, за которые мы дёргали редко (по сравнению с другими ручками). Поскольку числитель дроби растёт гораздо медленнее, чем знаменатель, при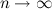 эвристика становится всё больше похожа на простой выбор ручки с оптимальным средним. Однако если какой-то из ni совсем перестанет расти (мы совсем разочаруемся в одной из ручек), рано или поздно даже логарифмический числитель заставит нас её ещё раз перепроверить.
эвристика становится всё больше похожа на простой выбор ручки с оптимальным средним. Однако если какой-то из ni совсем перестанет расти (мы совсем разочаруемся в одной из ручек), рано или поздно даже логарифмический числитель заставит нас её ещё раз перепроверить.
Реализация этого алгоритма на вашем любимом языке, понятное дело, никаких трудностей не представляет – нужно просто запоминать, сколько раз дёргали за каждую ручку. Главный пафос здесь в том, что хорошо работает такая простая эвристика: можно просто выбирать ручку с максимальным приоритетом и больше ни на что не обращать внимания. Это связано с так называемой теоремой Гиттинса: оказывается, что в достаточно общих предположениях выбор оптимальной стратегии в задаче о многоруких бандитах сводится к подсчёту независимых приоритетов для каждой ручки в отдельности. Правда, теорема Гиттинса сама по себе даёт только крайне сложный и медленный алгоритм вычисления этих приоритетов (так называемых индексов Гиттинса), и алгоритм UCB – это не просто частный случай общей теоремы, а отдельный результат.
В следующей серии мы продолжим рассматривать «бандитские» задачи и обобщим их до задач следования за трендами, когда доходы разных «ручек» могут изменяться во времени, и наша задача – быстро понимать, что и где изменилось.
Краткое содержание предыдущих серий о рекомендательных системах:
- рекомендательные системы: постановка задачи;
- user-based и item-based коллаборативная фильтрация;
- SVD, часть I;
- SVD и базовые предикторы;
- SVD на Perl;
- оверфиттинг и регуляризация;
- теорема Байеса и наивный Байес;
- LDA (Latent Dirichlet allocation, тематическое моделирование).
В этот раз начинаем новую тему – о многоруких бандитах. Бандиты – это самая простая, но от этого только более важная постановка задачи в так называемом обучении с подкреплением…

Мы всё время говорим, что то, что мы делаем, – это машинное обучение (machine learning). Однако задумайтесь: как вы на самом деле обучаетесь? Неужели мы с вами строим регрессию движения пальцев на основе наблюдений за машинистками для того, чтобы научиться слепой печати? Неужели ребёнок, чтобы научиться ходить, сначала собирает и обобщает коллекцию примеров прямохождения родителей? На самом деле, конечно, нет: в таких случаях мы просто пробуем что-нибудь сделать, смотрим, получилось ли, а затем пытаемся (обычно бессознательно) скорректировать своё поведение на основе полученного результата.
Такая постановка задачи называется обучением с подкреплением: есть агент, который действует в какой-то среде; агент пытается что-то делать, а среда в ответ на его действия выдаёт агенту плюшки или, наоборот, бьёт током. Агент старается получить плюшек побольше, а током – пореже. В общем, типичная мышка в лабиринте.
Сегодня, однако, мы поговорим о мышке, которая попала даже не в лабиринт, а в самый обычный skinner box – давайте предположим, что состояние среды/агента от действия к действию не изменяется. Иначе говоря, у агента есть некоторый набор возможных действий, агент выбирает одно из них, получает за это некоторое вознаграждение (которое является случайной величиной), а затем снова может выбирать из тех же действий. В машинном обучении такая постановка задачи получила название многоруких бандитов (multiarmed bandits): вы сидите в комнате перед несколькими игровыми автоматами и должны постараться выиграть как можно больше.

(картинка с сайта Microsoft Research)
Зачем это нужно в реальной жизни? К примеру, представьте себе, что вы – Yahoo! или, скажем, mail.ru. У вас есть домашняя страница, на которой бывают миллионы людей каждый день. Вы хотите размещать на ней ссылки так, чтобы на них кликали как можно чаще. Как выбрать те ссылки, которые дают максимальный CTR (click-through ratio)? Здесь каждый показ ссылки пользователю соответствует «дёрганию за ручку»; каждый клик – успех, положительное подкрепление от среды; не-клик – неудача. Задача алгоритма будет в том, чтобы как можно быстрее понять, что та или иная новость «горяча», и начать её показывать (да, это чуть модифицированная задача, в которой бандиты время от времени умирают и рождаются вновь).
Другой пример: представьте себе, что вы хотите протестировать какой-то набор изменений в интерфейсе своего сайта. Обычно это делается при помощи так называемого A/B testing – вы должны выбрать группу для эксперимента (по каждому изменению в отдельности), контрольную группу, для которой ничего не изменится, затем собрать статистику и оценить, значимо ли улучшение. Однако такая схема сама по себе не отвечает на главный вопрос – как долго надо собирать статистику? Здесь бандиты тоже могут придти на помощь, постановка задачи ведь в точности бандитская: показ того или иного варианта соответствует дёрганию за ручку, а действия пользователя определяют ответ окружающей среды (см., например, вот этот пост).
Однако вернёмся к постановке задачи. На первый взгляд кажется, что задача выбрать оптимальную ручку очень простая: нужно дёрнуть за каждую ручку по тысяче раз, а потом выбрать ручку с наибольшим средним. И действительно, такой алгоритм, скорее всего, сделает правильный выбор – но сколько он потеряет «денег» на субоптимальных ручках! Многих из этих потерь можно было бы избежать. Вообще, лучшая метрика для оценки качества «бандитского» алгоритма – это его потери (regret) по сравнению с оптимальным алгоритмом, т.е. ожидание разности дохода от стратегии «всегда дёргать за оптимальную ручку» и рассматриваемой стратегии.
В качестве примера я сразу приведу алгоритм с одними из самых лучших гарантий на эту самую меру потерь на обучение. Это алгоритм UCB1; сам алгоритм очень простой, доказательство его оптимальности, конечно, не такое простое, но в это мы углубляться не будем, а интересующихся я отсылаю к статье [Auer et al., 2002]; там же можно найти и более «продвинутую» версию с улучшенными константами.
- Инициализация: дёрнуть за каждую ручку один раз.
- Пока продолжается работа:
- дёрнуть за ручку j, для которой максимальна величина
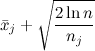 ,
,
где – средний доход от ручки j, nj – то, сколько раз мы дёрнули за ручку j, а n – то, сколько раз мы дёргали за все ручки.
– средний доход от ручки j, nj – то, сколько раз мы дёрнули за ручку j, а n – то, сколько раз мы дёргали за все ручки.
- дёрнуть за ручку j, для которой максимальна величина
Хотя формальное доказательство того, что здесь должно быть именно два натуральных логарифма, а не что-то другое, выходит за пределы этой статьи, интуитивно совершенно понятно, что происходит в этом алгоритме: мы придумали эвристику, оценку приоритета, по которой мы выбираем, за какую ручку дёргать. Логично, что этот приоритет тем больше, чем больше средний доход, но не только: бонус также получают те ручки, за которые мы дёргали редко (по сравнению с другими ручками). Поскольку числитель дроби растёт гораздо медленнее, чем знаменатель, при
 эвристика становится всё больше похожа на простой выбор ручки с оптимальным средним. Однако если какой-то из ni совсем перестанет расти (мы совсем разочаруемся в одной из ручек), рано или поздно даже логарифмический числитель заставит нас её ещё раз перепроверить.
эвристика становится всё больше похожа на простой выбор ручки с оптимальным средним. Однако если какой-то из ni совсем перестанет расти (мы совсем разочаруемся в одной из ручек), рано или поздно даже логарифмический числитель заставит нас её ещё раз перепроверить.Реализация этого алгоритма на вашем любимом языке, понятное дело, никаких трудностей не представляет – нужно просто запоминать, сколько раз дёргали за каждую ручку. Главный пафос здесь в том, что хорошо работает такая простая эвристика: можно просто выбирать ручку с максимальным приоритетом и больше ни на что не обращать внимания. Это связано с так называемой теоремой Гиттинса: оказывается, что в достаточно общих предположениях выбор оптимальной стратегии в задаче о многоруких бандитах сводится к подсчёту независимых приоритетов для каждой ручки в отдельности. Правда, теорема Гиттинса сама по себе даёт только крайне сложный и медленный алгоритм вычисления этих приоритетов (так называемых индексов Гиттинса), и алгоритм UCB – это не просто частный случай общей теоремы, а отдельный результат.
В следующей серии мы продолжим рассматривать «бандитские» задачи и обобщим их до задач следования за трендами, когда доходы разных «ручек» могут изменяться во времени, и наша задача – быстро понимать, что и где изменилось.
 ,
, – средний доход от ручки j, nj – то, сколько раз мы дёрнули за ручку j, а n – то, сколько раз мы дёргали за все ручки.
– средний доход от ручки j, nj – то, сколько раз мы дёрнули за ручку j, а n – то, сколько раз мы дёргали за все ручки.