
Перевод поста Эда Пегга Младшего (Ed Pegg Jr) "Martin Gardner’s 100th Birthday"
Я думаю, содержание этого поста будет интересно всем, кто любит математику и ее красоту, всем, кто знаком с замечательными книгами и задачами Мартина Гарднера, а также будет полезно учителям, школьникам и студентам. Все ссылки в данном посте ведут на сайты Wolfram Demonstrations Project (коллекция бесплатных интерактивных демонстраций, созданных пользователями системы Mathematica на языке Wolfram Language с помощью технологии Computable Document Format (CDF), при этом для вас доступны исходные коды всех демонстраций, а значит, вы можете каждую из них скачать, изучить и изменить под себя) и Wolfram MathWorld (крупнейшая и самая авторитетная онлайн-энциклопедия по математике).

Сто лет назад, 21 октября 1914 г., в Оклахоме родился Мартин Гарднер.
Коротко о Мартине Гарднере (материал из википедии)
Был ведущим рубрики математических игр и развлечений журнала «Scientific American», в которой была представлена широкой общественности игра «Жизнь», изобретенная Джоном Конвеем, а также многие другие интересные игры, задачи, головоломки.
Особую популярность снискали статьи и книги Гарднера по занимательной математике. Гарднер трактовал занимательность как синоним увлекательного, интересного в познании, но чуждого праздной развлекательности.
Известен также как автор нескольких фантастических рассказов («Остров пяти красок», «Нульсторонний профессор»), комментатор Льюиса Кэрролла («Алисы в Стране чудес», «Алисы в Зазеркалье» и «Охоты на Снарка») и Г. К. Честертона («Человека, который был четвергом» и «Неведения отца Брауна»).
Среди произведений Гарднера есть философские эссе, очерки по истории математики, математические фокусы и «комиксы», научно-популярные этюды, научно-фантастические рассказы, задачи на сообразительность.
«Гарднеровский» стиль характеризуют доходчивость, яркость, убедительность изложения, блеск, парадоксальность мысли, новизна и глубина научных идей, многие из которых почерпнуты из современных научных публикаций и в свою очередь стали стимулом проведения серьёзных исследований, активного вовлечения читателя в самостоятельное творчество.
Особую популярность снискали статьи и книги Гарднера по занимательной математике. Гарднер трактовал занимательность как синоним увлекательного, интересного в познании, но чуждого праздной развлекательности.
Известен также как автор нескольких фантастических рассказов («Остров пяти красок», «Нульсторонний профессор»), комментатор Льюиса Кэрролла («Алисы в Стране чудес», «Алисы в Зазеркалье» и «Охоты на Снарка») и Г. К. Честертона («Человека, который был четвергом» и «Неведения отца Брауна»).
Среди произведений Гарднера есть философские эссе, очерки по истории математики, математические фокусы и «комиксы», научно-популярные этюды, научно-фантастические рассказы, задачи на сообразительность.
«Гарднеровский» стиль характеризуют доходчивость, яркость, убедительность изложения, блеск, парадоксальность мысли, новизна и глубина научных идей, многие из которых почерпнуты из современных научных публикаций и в свою очередь стали стимулом проведения серьёзных исследований, активного вовлечения читателя в самостоятельное творчество.
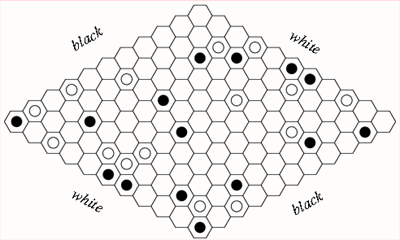
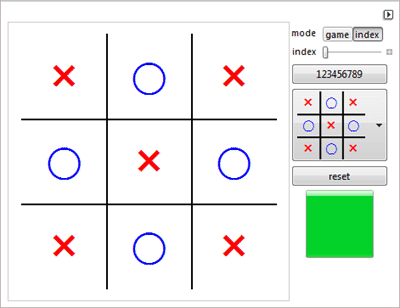
Он писал о игре гекс и крестики-нолики.
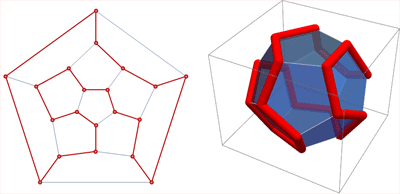
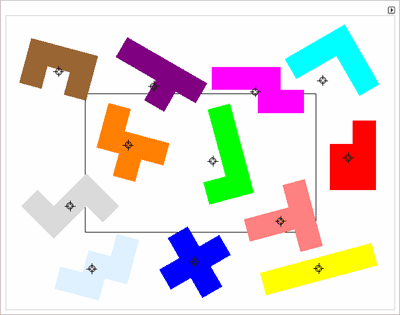
Поиске гамильтоновых циклах на ребрах додекаэдра (игра “Икосиан”) и о полиомино.
Флексагонах из бумаги, пазлах Сэмюэля Лойда, и игре Ним.



Цифровом корне из числа, кубиках Сома, лабиринтах, логике, и магических квадратах.
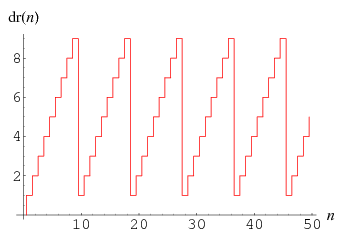
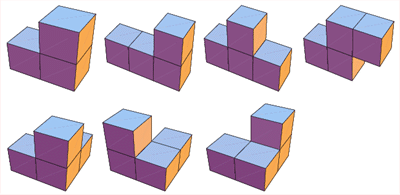


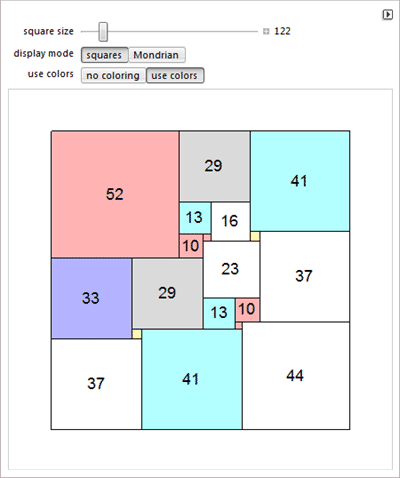
Квадрировании квадрата и золотом сечении.
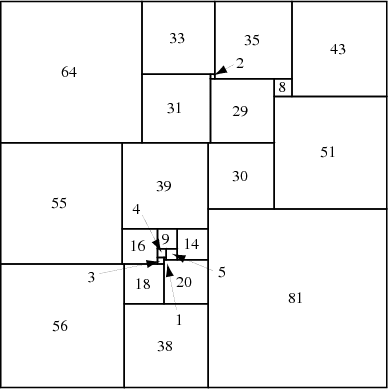
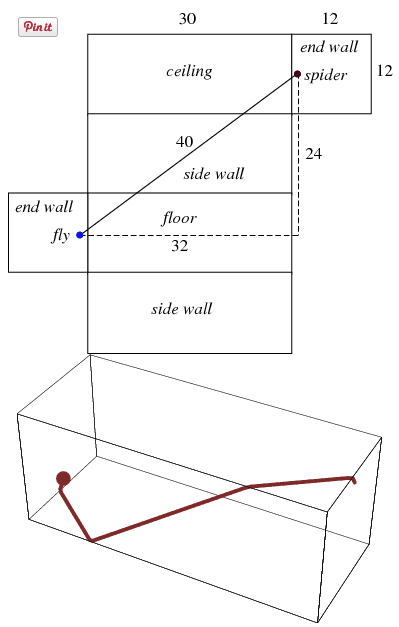
Решил "задачу о пауке и мухе".
Писал о задаче упаковки кругов, свойствах эллипса, числа пи и конических сечений.


Теории групп и ее применении в теории кос, интервалах между простыми числами, латинских квадратах, теореме о четырех красках.
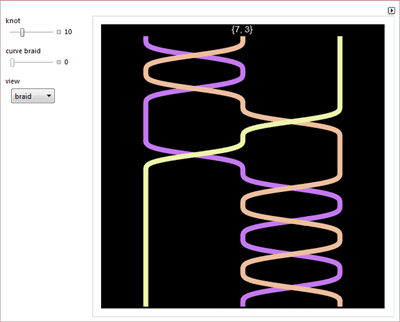
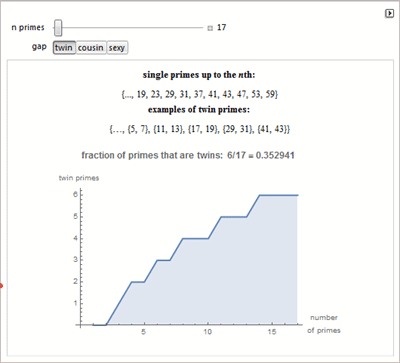
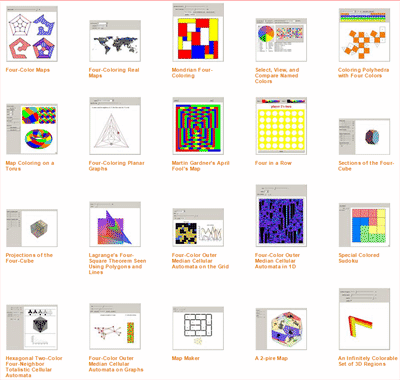
Гиперкубах, машинах Тьюринга, кривых постоянной ширины, задаче о восьми ферзях.
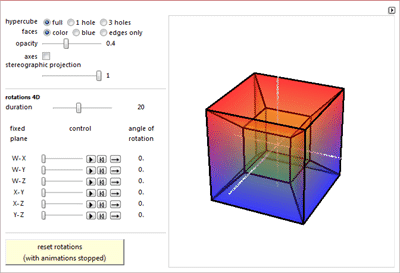


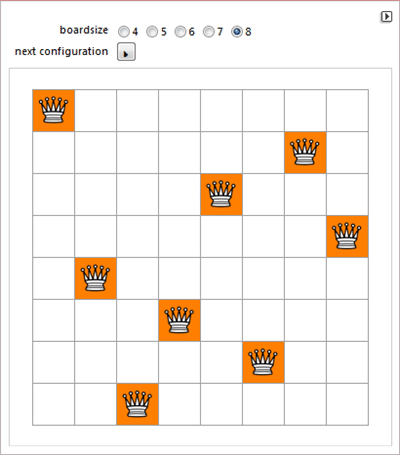
Бутылке Клейна, разрезанной на ленты, винтовых линиях и "изящных графах".
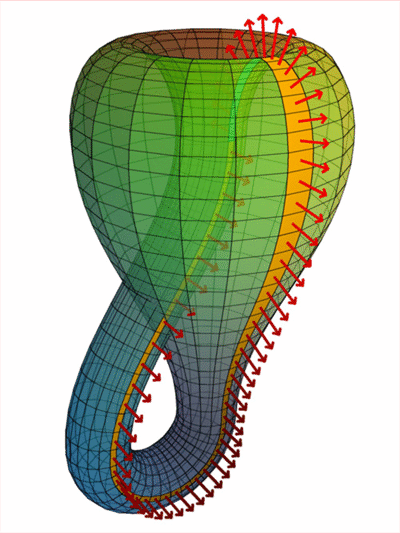


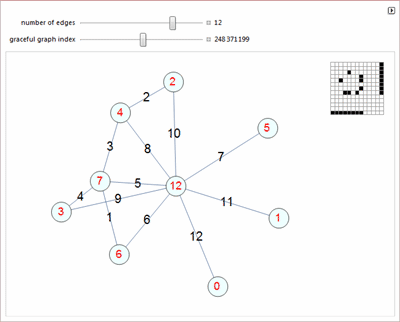
О послании Аресибо, и признаках делимости чисел.

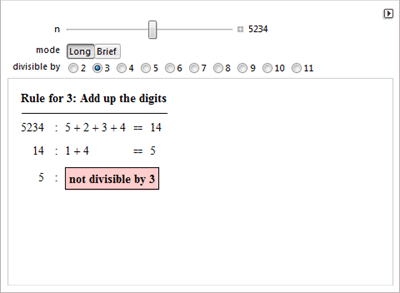
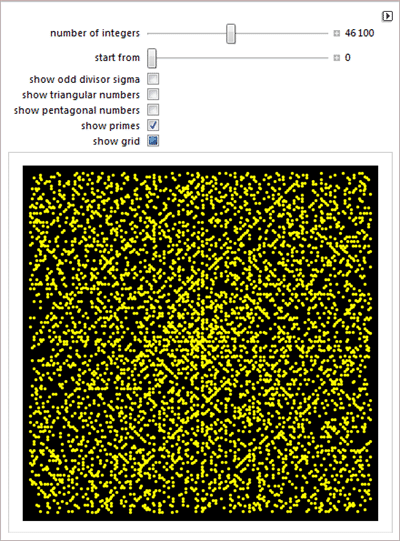
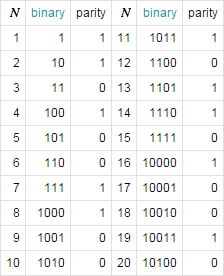
О коврах Улама и четности/нечетности чисел.
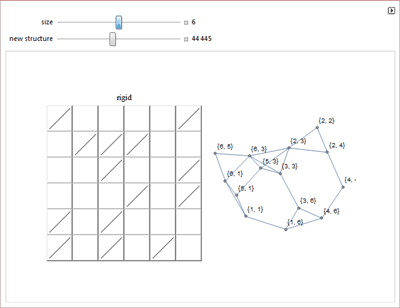
Зданиях на основе ферм, которые будут устойчивы, трисекции угла, и задаче о одеяле миссис Перкинс.

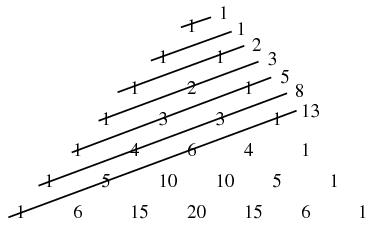
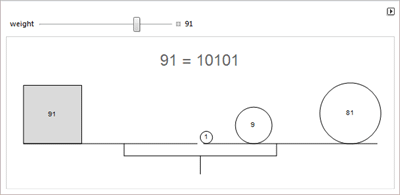
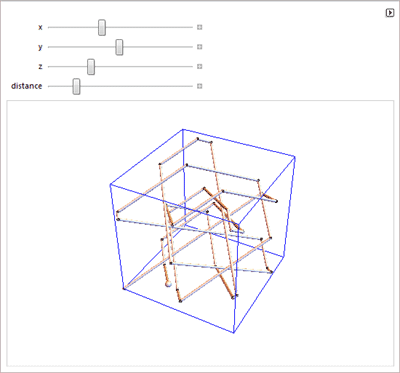
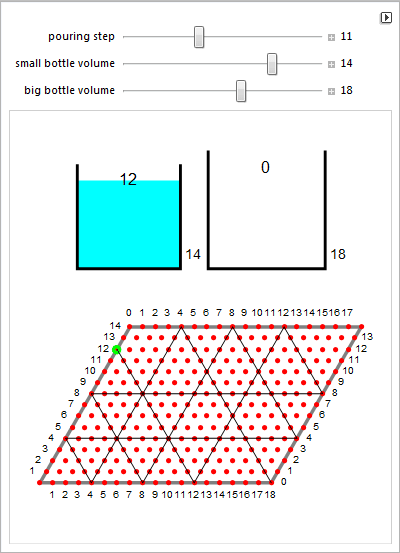
О треугольнике Паскаля, уравновешивании весов с троичными весами и задаче о бильярдной траектории применительно к задаче о переливании воды.
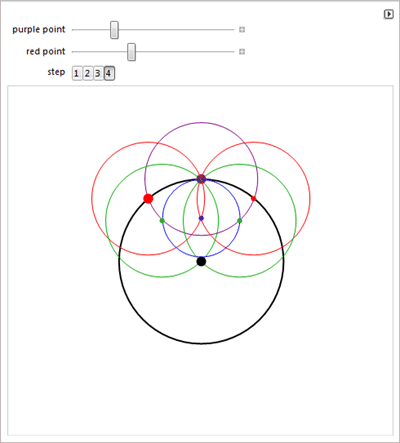
О геометрических построениях с ограничениями , числе e и доказательстве задач по индукции.


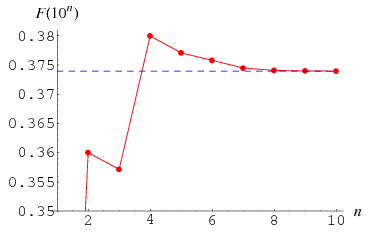
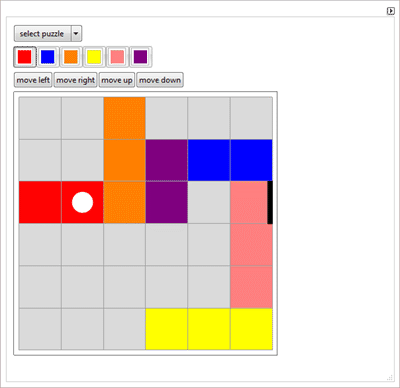
О абаке, случайных блужданиях, периодических десятичных дробях и пазлах типа пятнашек.


О теореме Пифагора, шестеренках, исскусстве М. К. Эшера и сферах.



Узорах на основе домино, башни на основе гармонического ряда, бесконечных рядах и задачи о разрезании пирога.

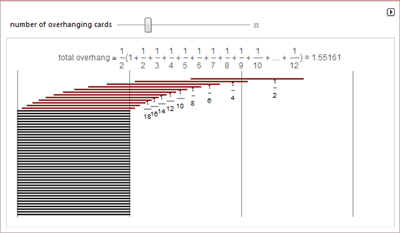

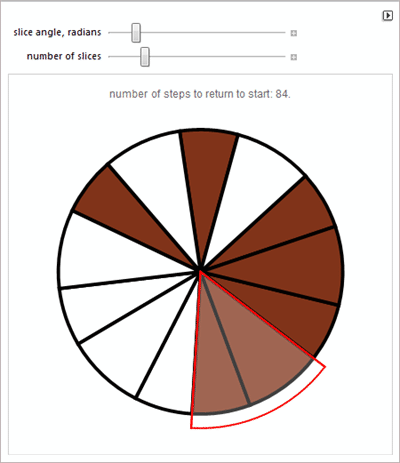
О Алеф-нуль и Алеф-один.
О Игре жизни и ружье Госпера.
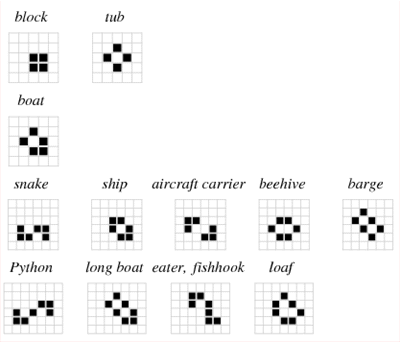
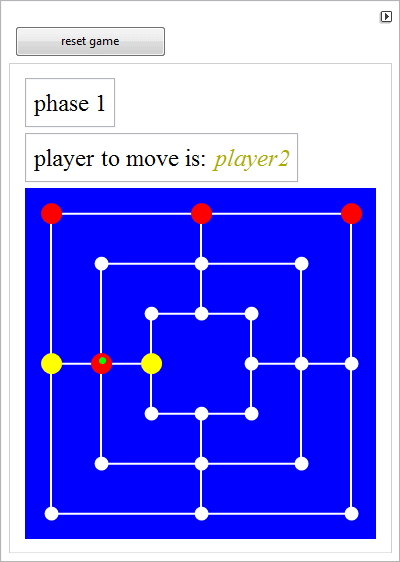
О червях Патерсона и скрученном в узел торе, сгибании листа бумаги и игре Мельница.
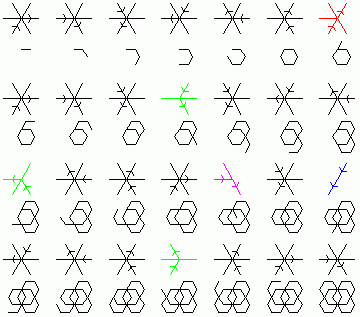

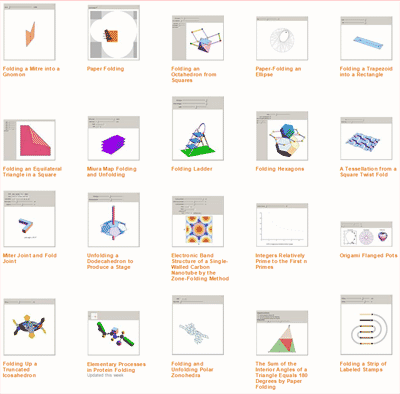
О проблеме, решенной Эндрю Уайлсом (Великая теорема Ферма).
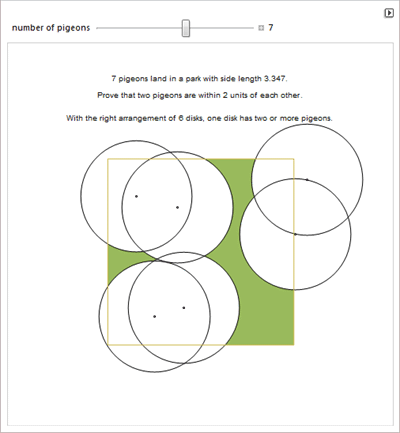
О принципе Дирихле и узорах Пенроуза.

О игре солитер, фигурах из нити, кривых дракона, и книге перемен.
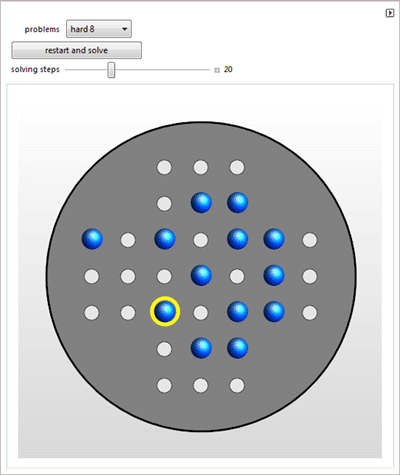
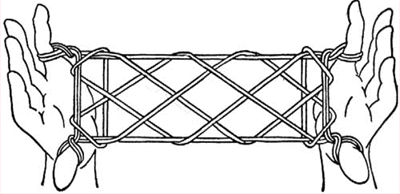


О фигурах, которые могут быть разбиты на подобные самой фигуре, и кольцах Борромео.
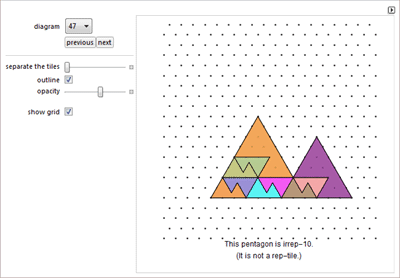

О замощении плоскости пятиугольниками, задаче о тасовании, задаче о "Точном касании ", тетраэдрах, циклоидах и кубике для игры в кости.
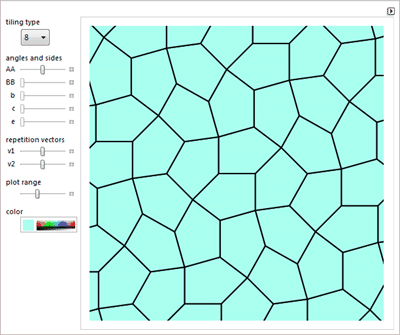
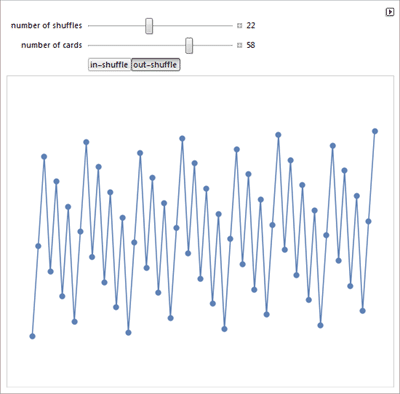
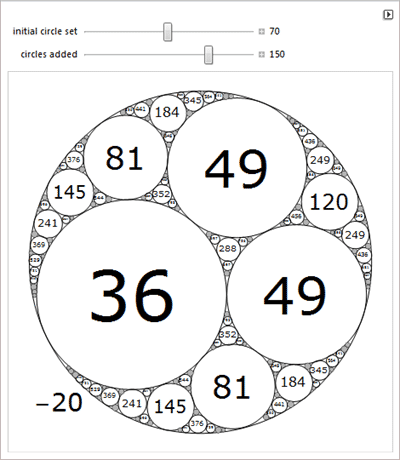
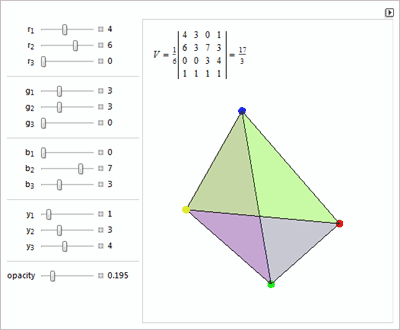


Диофантовых уравнениях и геометрических заблуждениях.


Нетранзитивных игральных костях и специальной теории относительности.
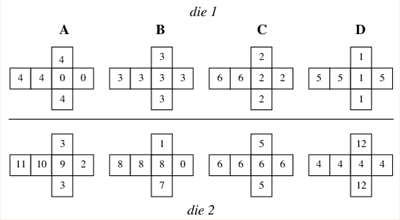

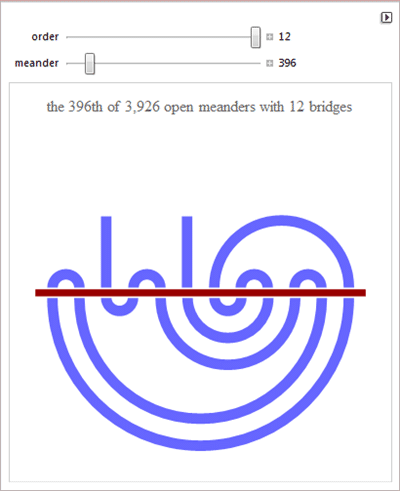
Меандры… на самом деле можно продолжать пожалуй не один день перечислять то, чем занимался и о чем писал Мартин Гарднер, но думаю, того, что я уже перечислил вполне достаточно, чтобы почтить его память.
Ресурсы для изучения Wolfram Language (Mathematica) на русском языке: http://habrahabr.ru/post/244451