
Скачать перевод в виде документа Mathematica, который содержит весь код использованный в статье, можно здесь (архив, ~76 МБ).
Введение
Некоторое время назад, если быть точным — 515 дней, вышел пост Маттиаса Одисио (Matthias Odisio) под названием “Random and Optimal Mathematica Walks on IMDb’s Top Films” (Случайные и оптимальные блуждания Mathematica по списку 250 лучших фильмов по версии IMDB). В нем рассказывается о том, каким образом можно получить оптимальную последовательность просмотра фильмов из соответствующего списка, основанную на близости жанров фильмов и близости постеров фильмов с точки зрения цвета.
In[1]:=
Out[1]=
Идея этого поста показалась мне довольно интересной, но мне захотелось её существенно расширить и углубить, следуя нескольким идеям:
- Построить более совершенную функцию, оценивающую близость фильмов, так как мне кажется, что построение функции расстояния между фильмами на основе близости постеров фильмов по использующимся в них цветам и жанрам фильмов не достаточно объективно. Мне представляется разумным построить функцию расстояния между фильмами на основе нескольких факторов: жанров фильма, описания фильма, актерского состава, режиссера(-ов), года производства, сценариста(-ов) и пр.
- В статье Маттиаса использовались лишь данные Wolfram|Alpha, что, безусловно, упрощает задачу и компактизирует код. Мне же хочется рассказать о том, как можно использовать в расчетах данные, взятые откуда угодно, например, полученные с помощью веб-парсинга со страниц Википедии, подгруженные из текстовых баз данных и т. п.
Я не буду рассказывать в этой статье о том, как построить оптимальную последовательность просмотра списка 250 лучших фильмов КиноПоиска по той причине, что просто не хочется иметь проблем с условиями использования данного ресурса, которые довольно четко говорят (см. п. 6), что просто взять их список фильмов и произвести его анализ без их согласия не получится. При этом применить алгоритмы, которые я приведу ниже для этого списка довольно просто. Также мне хотелось бы отметить, что во время моей работы с одной из отечественных кинокомпаний для их нужд на языке Wolfram Language был написан парсер, который подгружал информацию о фильмах с сайта КиноПоиск (юридическая сторона вопроса была улажена) для последующего автоматического формирования рекламного буклета о нескольких тысячах фильмов, права на которые принадлежали этой компании. Ниже вы можете видеть пример одной такой полностью автоматически созданной страницы буклета (приведена неокончательная версия, ввиду NDA).
Пример страницы

В данной статье будет использоваться информация о фильмах, представленная в Википедии, что позволит избежать любых проблем с правообладателями. Это с одной стороны усложняет задачу (парсер с централизованного хранилища вроде IMDB или КиноПоиска написать проще), но в тоже время позволяет построить некоторые дополнительные, интересные, программы.
Импорт данных с сайта Википедии
Для начала, подгрузим символьное представление HTML кода страницы Википедии “250 лучших фильмов по версии IMDb” (в документе отобразим при этом лишь часть результата с помощью функции Short):
In[2]:=
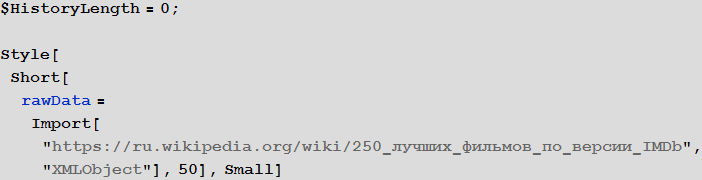
Out[3]=

Теперь выделим ссылки на фильмы, приведенные на странице в таблице:
In[4]:=

Out[4]=

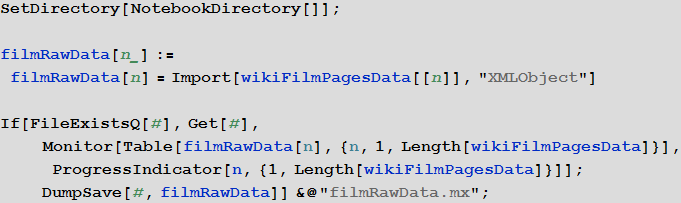
Создадим функцию, которая подгрузит и сохранит символьное представление HTML кода страниц каждого из фильмов:
In[5]:=
Вспомогательные функции
Создадим набор вспомогательных функций, который понадобится нам для обработки погруженного символьного HTML:
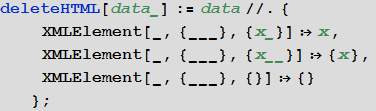
- Функция для удаления HTML-оберток, оставляющая только данные:
In[8]:=
- Функция, которая определяет, может ли быть некоторая строка словом на русском языке (т. е. состоит из букв русского алфавита или дефиса):
In[9]:=

In[10]:=
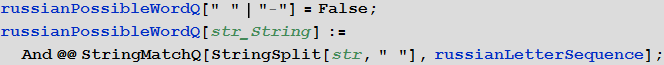
- Функция, которая определяет, может ли быть некоторая строка словом на русском или английском языке (т. е. состоит из букв русского, английского алфавита или дефиса):
In[12]:=

In[13]:=

- Функция, преобразующая (в строке) заглавные буквы русского алфавита в прописные:
In[15]:=

In[16]:=
- Для анализа описаний фильмов нам потребуется информация о словах русского языках и связях между формами одного и того же слова. Подгрузим морфологический словарь русского языка, созданный академиком Андреем Анатольевичем Зализняком:
In[17]:=

Out[17]=

- Обработаем данные словаря, составив на его основе список слов русского языка (russianWords) и список правил замены форм слов русского языка в их стандартную форму (russianWordsStandardForm):
In[18]:=
В словаре содержится 2 645 347 слов:
In[19]:=
Out[19]=
Out[20]=

- Создадим функцию, которая проверяет, содержится ли слово в словаре, а также функцию, преобразующую русское слово в его стандартную форму:
In[21]:=
In[22]:=
Примеры работы функций:
In[23]:=
Out[23]=
In[24]:=
Out[24]=
- Создадим функцию, которая будет устанавливать, является ли слово прилагательным:
In[25]:=

In[26]:=
Обработка данных
Теперь можно обработать данные каждого из фильмов. При этом на выходе в переменной filmsData будет храниться база данных информации о фильмах, построенная на основе функции Association, что позволит нам очень легко обращаться к данным.
In[27]:=

In[29]:=

Пример обращения к сформированной базе по номеру фильма:
In[31]:=
Out[31]=

Пример обращения с запросом о режиссёре и годе выхода каждого из фильмов:
In[32]:=
Out[32]//Short=

Немного статистики на основе данных
Для начала, просто сформируем коллаж из постеров всех фильмов:
In[33]:=
Out[33]=

Построим распределение количества фильмов в зависимости от года:
In[34]:=

Out[34]=

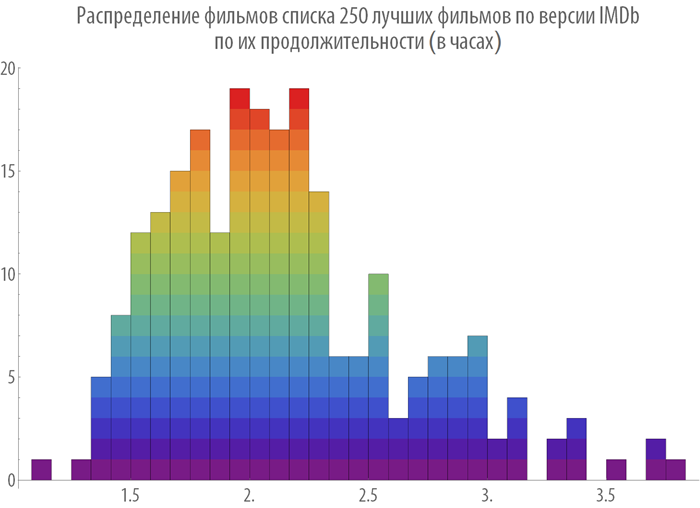
Построим распределение фильмов по их продолжительности:
In[35]:=

Out[35]=
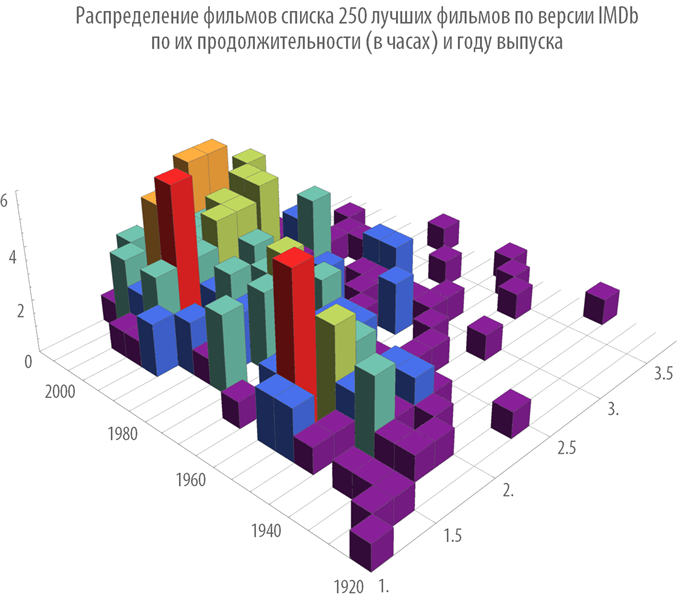
Построим распределение фильмов по их продолжительности и году выпуска:
In[36]:=

Out[36]=
Первые 10 актеров по количеству фильмов, в которых они сыграли:
In[37]:=

Out[37]=

Первые 10 режиссёров по количеству фильмов, которые они сняли:
In[38]:=

Out[38]=

Первые 10 сценаристов по количеству фильмов, сценарий к которым они написали:
In[39]:=

Out[39]=

Первые 10 композиторов по количеству фильмов, музыку к которым они написали:
In[40]:=

Out[40]=

Первые 10 стран по количеству фильмов, которые были в них сняты:
In[41]:=

Out[41]=

Первые 10 жанров по количеству фильмов, которые к ним относятся:
In[42]:=
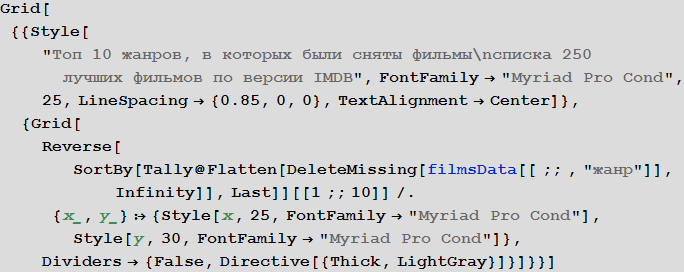
Out[42]=

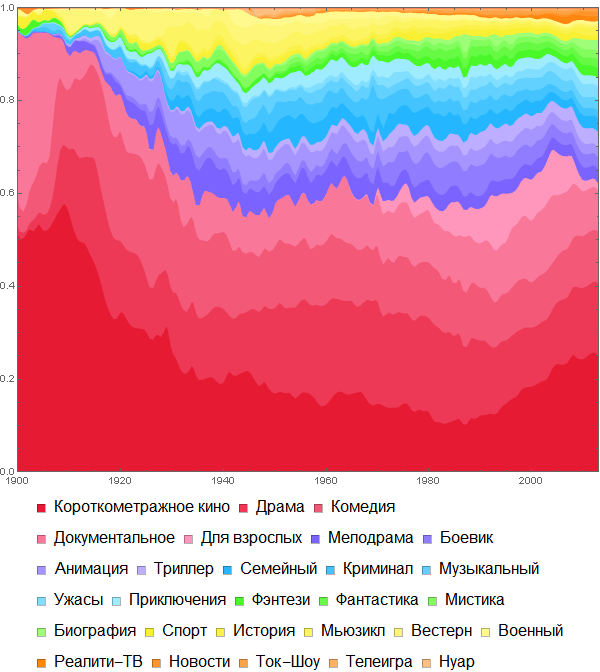
Для тех, кого интересуют жанры кино, могу порекомендовать написанную некоторое время назад статью “Фильмы и Mathematica: импорт и обработка информации из базы данных IMDB”, в которой, в частности, получено следующее распределение фильмов по жанрам:
Функция, определяющая расстояние между фильмами
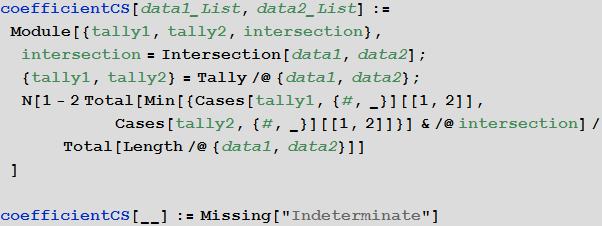
Для определения меры различия двух списков объектов мы будем использовать обобщение коэффициента (меры) Чекановского-Съёренсена:
In[43]:=
Пример:
In[45]:=
Out[45]=
Для определения близости описаний с помощью этого коэффициента создадим функцию, выбирающую из описания фильма слова русского языка с переводом их в стандартную форму:
In[46]:=

Пример работы функции (дополнительно было посчитана частота каждого слова с помощью функции Tally, при этом частоты были отсортированы по их уменьшению):
In[47]:=

Out[47]=

Теперь создадим функцию, определяющую степень близости фильмов между собой. Она представляет собой нормированную на единицу сумму нескольких параметров с разными весами. Всего взято 11 параметров (степеней) сходства: описание фильма, жанр(-ы), режиссёр, сценарист(-ы), актёры, оператор(-ы), композитор(-ы), страна(-ы) производства, год выхода, длительность, близость постеров. При этом можно задавать им разные веса, но по умолчанию они будут одинаковы.
In[48]:=

Выберем для дальнейшей работы те фильмы, для которых известна хоть какая-то информация (ввиду того, что для нескольких фильмов их страницы Википедии пусты):
In[62]:=

Вычислим все меры близости (расстояния) между фильмами:
In[63]:=

Анализ связей между фильмами
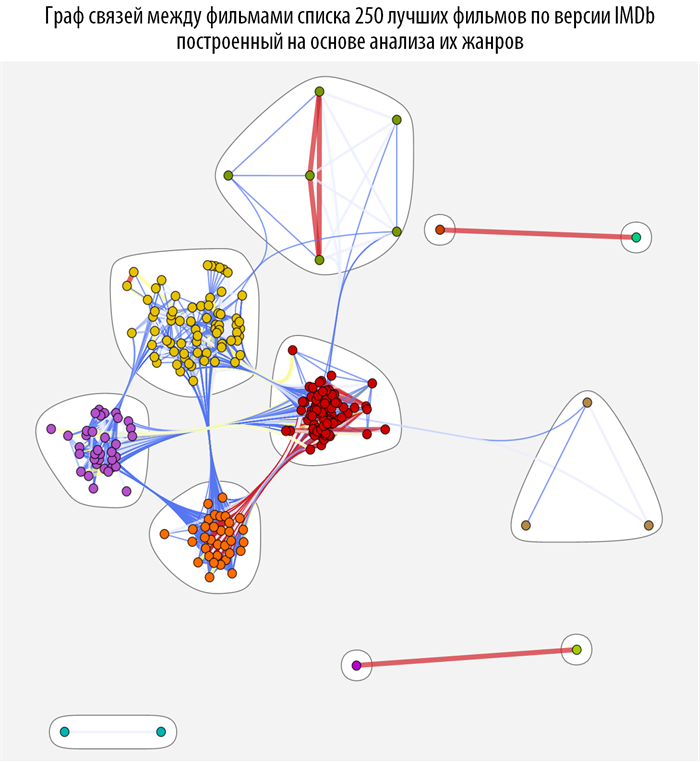
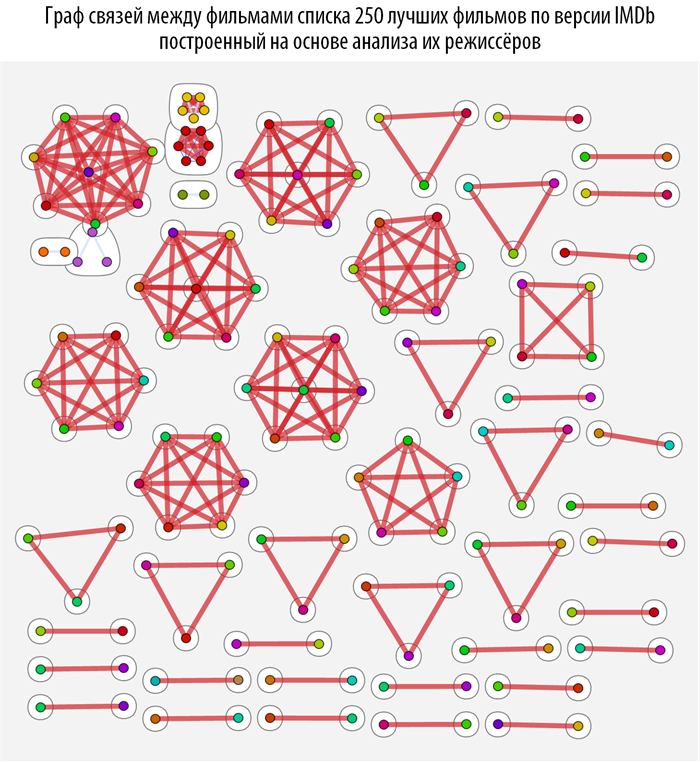
Изучим связи между фильмами с помощью методов теории графов, а именно с помощью теории о структуре комьюнити в графах. Для этого создадим функцию на основе CommunityGraphPlot:
In[64]:=

Данная функция ищет, на основе построенной ранее функции расстояния между фильмами, комьюнити в графе, при этом чем краснее и толще связь между вершинами, тем они теснее связаны (ближе). При наведении на каждую из вершин графа вы можете получить всплывающую подсказку с постером и названием фильма (скачать документ с интерактивными графами и исходным кодом вы можете по ссылке, приведенной в самом начале поста).

In[65]:=

Out[65]=

In[66]:=

Out[66]=
In[67]:=

Out[67]=
In[68]:=

Out[68]=

In[69]:=

Out[69]=

In[70]:=

Out[70]=

In[71]:=

Out[71]=
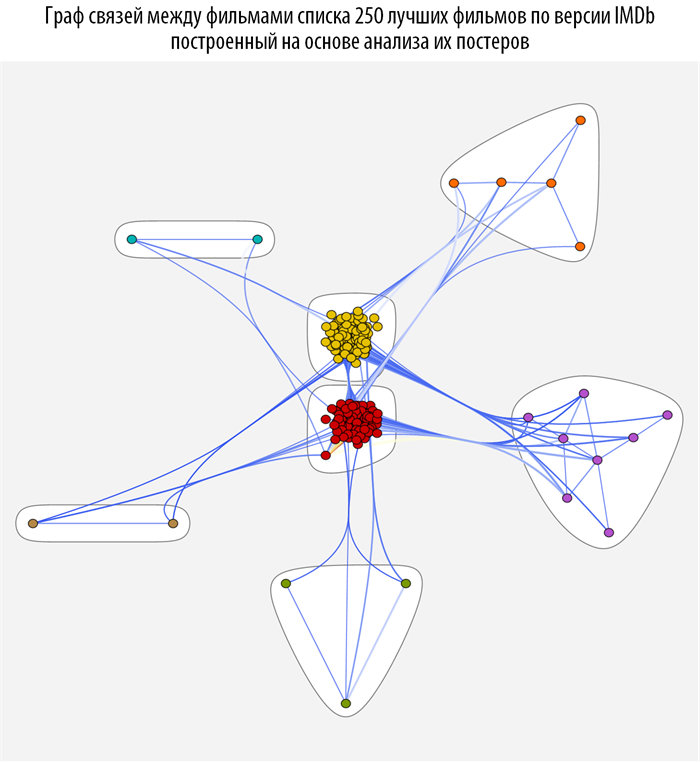
In[72]:=

Out[72]=
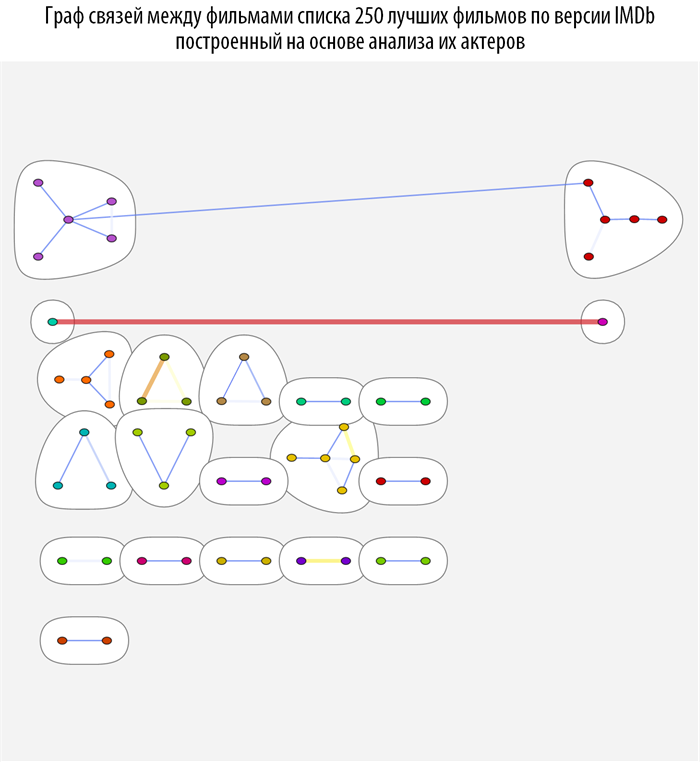
Построение оптимальной последовательности просмотра фильмов
Мы проделали довольно большую работу и теперь, наконец, можем построить оптимальную последовательность просмотра фильмов:
In[73]:=

Итак, теперь мы можем получить ее (функция предусматривает вывод либо в виде таблицы, либо в виде плаката из постеров):
In[74]:=

Таблица оптимальной последовательности просмотра фильмов из списка 250 лучших фильмов по версии IMDb
Out[74]=


Также, можно отобразить её в виде плаката из постеров (последовательность просмотра фильмов при этом будет слева направо, сверху вниз):
In[75]:=

Out[75]=

Мы может также рассмотреть оптимальные последовательности по отдельным критериям:
Последовательность просмотра на основе описания фильма
In[76]:=

Out[76]=


Out[76]=

Последовательность просмотра на основе жанра фильма
In[77]:=

Out[77]=


Out[77]=

Последовательность просмотра на основе актерского состава фильма
In[78]:=

Out[78]=


Out[78]=

Последовательность просмотра на основе режиссёра фильма
In[79]:=

Out[79]=


Out[79]=

Последовательность просмотра на основе сценаристов фильма
In[80]:=

Out[80]=


Out[80]=

Последовательность просмотра на основе композиторов фильма
In[82]:=

Out[82]=


Out[82]=

Последовательность просмотра на основе длительности фильма
In[83]:=

Out[83]=


Out[83]=

Последовательность просмотра на основе постера фильма
In[84]:=

Out[84]=


Out[84]=

Последовательность просмотра на основе страны производства фильма
In[85]:=

Out[85]=


Out[85]=

Заключение
Надеюсь, что мой пост смог заинтересовать вас, а некоторые идеи и программы, представленные в нем окажутся вам полезны. Безусловно, можно придумать множество путей применения этих алгоритмов, их дальнейшего расширения и совершенствования. Многие вещи были специально упрощены мной, так как не все готовые коды могут быть выложены полностью в свободном доступе. Думаю, что если вам будет интересно, вы можете самостоятельно создать парсер с КиноПоиска или IMDB напрямую (в последнем случае вам может помочь статья о подгрузке и анализе информации из баз данных IMDB, выложенных этим ресурсов в свободном доступе) и на его основе уже произвести еще более подробный и качественный анализ кино, а также улучшить полученную в этой статье оптимальную последовательность просмотра фильмов. Надеюсь, что все эти задачи заинтересуют и вас!
Ресурсы для изучения Wolfram Language (Mathematica) на русском языке: http://habrahabr.ru/post/244451