
Перевод поста Matthias Odisio "Seeing Skin with Mathematica".
Скачать файл, содержащий текст статьи, интерактивные модели и весь код, приведенный в статье, можно здесь.
Выражаю огромную благодарность Кириллу Гузенко за помощь в переводе.
Детекция кожи может быть довольно полезной — это один из основных шагов к более совершенным системам, нацеленным на обнаружение людей, распознавание жестов, лиц, фильтрации на основе содержания и прочего. Несмотря на всё вышеперечисленное, моя мотивация при создании приложения заключалась в другом. Отдел разработки и исследований в Wolfram Research, в котором я работаю, подвергся небольшой реорганизации. С моими коллегами, которые занимаются вероятностями и статистикой, которые стали находиться ко мне значительно ближе, я решил разработать небольшое приложение, которое использовало бы как функционал по обработке изображений в Mathematica, так и статистические функции. Детекция кожи — первое, что пришло мне в голову.
Оттенки кожи и внешность могут варьироваться, что усложняет задачу детекции. Детектор, который я хотел разработать, основывается на вероятностных моделях для цветов пикселей. Для каждого пикселя изображения, поданного на вход, детектор кожи выдаёт вероятность того, что этот пиксель принадлежит области кожи.
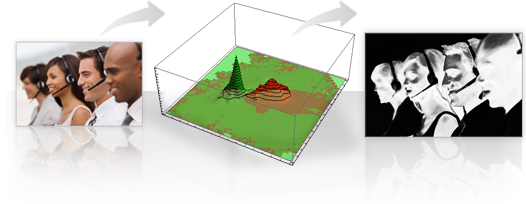
Давайте рассмотрим эту задачу с точки зрения теории вероятностей. Мы хотели бы оценить вероятность того, что пиксель принадлежит области с кожей заданного цвета. Используя формулу Байеса, мы можем выразить это так (назовём это уравнением 1):
Обратите внимание на то, что в этом посте вероятности обозначаются заглавной P[.].
Три условия в правой части уравнения могут быть представлены в вычислимой форме. Тут нам пригодятся вероятностный подход и эти два обучающих набора данных: первый состоит из пикселей, принадлежащих областям с кожей, а второй — из пикселей не принадлежащих. Мы обучим статистическую модель и получим формулу для P[color|skin]. Оценка априорной P[skin] может быть произвольной в том смысле, что она зависит от конечного приложения, для которого разрабатывается детектор кожи. Мы пойдём простым путём и определим априорную вероятность через отношение количества пикселей из двух обучающих наборов данных. С P[color] сначала будет больше проблем, потому что надежное моделирование вероятностей для каждого возможного цвета потребует огромного обучающего набора данных. К счастью, формула полной вероятности позволяет нам обойти эту проблему путём разложения этого члена следующим образом:
Наконец, наш вероятностный детектор кожи будет реализован формулой (назовём её уравнением 2):
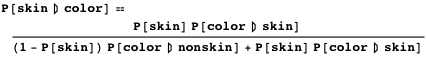
Давайте теперь создадим две подборки изображений и обучим нашу модель на них.
Мне не понаслышке известно, что создание подобных подборок — нечто вроде искусства, и требует большого количества усилий. Однако на этот раз мы не будем особо усердствовать и соберём вместо этого лишь с дюжину изображений, на которых изображена кожа. Конечно, для серьёзных статистически значимых моделей потребовались бы сотни изображений и сложные модели кожи.
Используя меню Graphics в Mathematica, я могу вручную выбрать области с кожей в изображении и повторить процесс для подборок с изображениями — честно говоря, не самая интересная часть моего дня:

Есть сведения, что стандартное цветовое пространство RGB не является лучшим цветовым пространством для реализации моделей с разделением цветов по критерию кожа/не кожа. Большинство проблем может возникать из-за того, что при разном освещении и разных чертах лица кожа выглядит по разному.
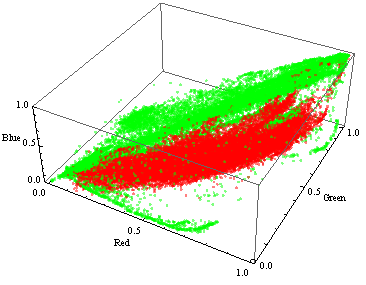
Как можно увидеть, цвета кожи и всего помимо неё (изображённые в красном и зелёном цветах соответственно) не сильно перекрываются в изображениях в выборке, но при этом охватывают большую часть трёхмерного пространства RGB:
Давайте поэкспериментируем с другим цветовым пространством, где подобные изменения в том, как выглядит кожа, моделируются, пожалуй, более надёжно.
В качестве цветового пространства можно выбрать CIE XYZ, а цвета кожи представить в двух цветовых и одной яркостной координатах. Чтобы разработать модели, более устойчивые к изменениям в условиях освещения, мы будем работать лишь с цветовыми координатами x и y, определяемыми как x = X / (X + Y + Z) и y = Y / (X + Y + Z):
Функция colorConvertxy дает двухканальное xy изображение:
![colorConvertxy[img_] := ImageApply[Most[#]/(Total[#] + $MachineEpsilon) &, ColorConvert[img, "XYZ"]]; colorConvertxy[img_] := ImageApply[Most[#]/(Total[#] + $MachineEpsilon) &, ColorConvert[img, "XYZ"]];](https://habrastorage.org/getpro/habr/post_images/15b/68e/1ae/15b68e1ae679d84fde1710521d263d45.png)
Извлечение списка пар xy регионов с кожей осуществляется с использованием самого изображения, маски областей кожи и функций PixelValuePositions и PixelValue. Список пар xy областей изображения без кожи можно получить точно таким же способом.

В двумерном xy цветовом пространстве области с координатами точек кожи для всех тренировочных изображений имеют меньшую площадь, чем в RGB, а разница между областями с кожей и без менее выражена. В представленных ниже распределениях для цветов областей с кожей и без первые представлены в оттенках зелёного, а вторые в оттенках красного.


Работа в двумерном xy цветовом пространстве представляется многообещающей. Давайте вернёмся назад и представим основанные на данных статистические модели для уравнения 2. Для удобства читателя приведём формулу повторно:
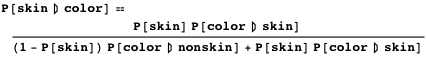
Доля пикселей с кожей среди миллиона пикселей обучающего набора данных составляет примерно 13%. Сохраним это эмпирическое значение в нашей модели для априорной вероятности P[skin]:
Для моделирования функций плотности вероятностей P[color|skin] и P[color|nonskin] приходит на ум использовать некую смесь распределений Гаусса. Эти распределения вполне могут подойти для данных пар xy, представленных выше. Однако на моем ноутбуке вычисления совершаются немного быстрее при выборе модели, основанной на распределениях со сглаженным ядром ядерном (smooth kernel distributions), которые строятся с помощью функции SmoothKernelDistribution:
Наконец, вероятность того, что данный цвет в xy соответствует коже, можно представить через следующую функцию:
![probabilityskin = Function[{x, y}, Evaluate[(pskin PDF[ pcolorskin, {x, y}])/((1 - pskin) PDF[pcolornonskin, {x, y}] + pskin PDF[pcolorskin, {x, y}] + $MachineEpsilon)]]; probabilityskin = Function[{x, y}, Evaluate[(pskin PDF[ pcolorskin, {x, y}])/((1 - pskin) PDF[pcolornonskin, {x, y}] + pskin PDF[pcolorskin, {x, y}] + $MachineEpsilon)]];](https://habrastorage.org/getpro/habr/post_images/e7a/bf9/145/e7abf91454cdaf94256c54e08c14981d.png)

Как будет работать представленная модель? Давайте применим функцию к нескольким тестовым изображениям:
![skinness[image_] := ImageApply[probabilityskin[Sequence @@ #] &, colorConvertxy[image]]; skinness[image_] := ImageApply[probabilityskin[Sequence @@ #] &, colorConvertxy[image]];](https://habrastorage.org/getpro/habr/post_images/b00/103/319/b00103319b5bbe01d42be9590f4b0c3f.png)


Не плохо, не так ли? А вот с другим тестовым изображением ниже получается интересно — размытая область на границе между красной футболкой и зеленой листвой некорректно с высокой вероятностью определяется как кожа.


Всё почти готово. По сути, детекция кожи требует принятия решения о том, принадлежит ли пиксель коже. Для создания подобного бинарного изображения мы могли бы установить порог для полученных нами изображений. Однако какой порог выбрать? Если выбрать слишком высокий, то пиксели кожи могут не обнаружиться. Если выбрать слишком низкий, то велико будет количество определённых как кожа пикселей без кожи. Всё это ведёт к построениям и анализу ROC-кривых. Да, было бы здорово воссоздать подобный функционал с Mathematica, однако я считаю, что данная тема заслуживает большего внимания. В общем, в другой раз, в другом посте.
В альтернативной стратегии предлагается сравнивать вероятности для пикселя быть частью области с кожей или нет. Как и в прошлый раз, давайте воспользуемся вероятностным подходом и пересмотрим уравнение 1: P[skin|color] == P[color|skin]*P[skin]/P[color]. Точно так же можно выразить апостериорную вероятность того, что данный пиксель не принадлежит области с кожей:
Чтобы отсортировать этот цвет по критерию кожа/не кожа, нам нужно просто сравнить полученные апостериорные вероятности и выбрать большую. P[color] можно отбросить, и тогда пиксель будет определяться как принадлежащий области с кожей, если P[color|skin]*P[skin] > P[color|nonskin]*P[nonskin].
Вот как работает на данный момент детектор кожи:

Быстрая оценка тестовых изображений позволяет заключить, что система вполне справляется с поставленной задачей:


Давайте завершим эту тему приложением по детекции кожи:


Изначально моей целью было создать детектор кожи чисто из удовольствия в исследовании взаимодействий между вероятностями, статистикой и обработкой изображений. Практически каждый элемент нашей окончательной версии детектора кожи (например, обучающая выборка, выбор статистических распределений, классификатора, количественной оценки) может быть изучен более детально и улучшен, используя широкий функционал Mathematica.