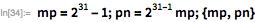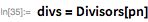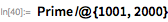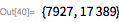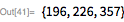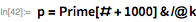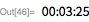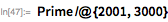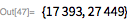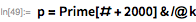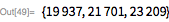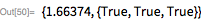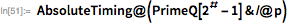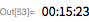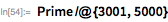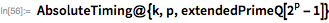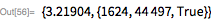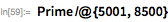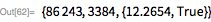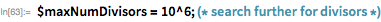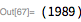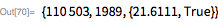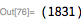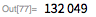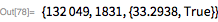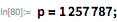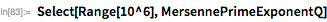Перевод поста Джона Макги (John McGee) "Mersenne Primes and the Lucas–Lehmer Test".
Код, приведенный в статье, можно скачать здесь.
Выражаю огромную благодарность Полине Сологуб за помощь в переводе и подготовке публикации.
Содержание
—
Введение.
—
Теорема множителей Эйлера и Мерсенна
—
Люка и Лемер
—
От  до
до 
—
Совершенные числа
—
21-е, 22-е и 23-е числа Мерсенна
—
24-е, 25-е и 26-е числа Мерсенна.
—
27-е и 28-е числа Мерсенна
—
29-е число Мерсенна
—
30-е и 31-е числа Мерсенна
—
Великий интернет-поиск чисел Мерсенна
—
Факторизация чисел Мерсенна
Введение
Простое число Мерсенна — простое число вида

(значение степени
р также должно быть простым). Эти простые числа получили свое название от имени французского математика и религиозного ученого
Мерсенна, который и составил данный список простых чисел этой формы в первой половине семнадцатого века. Первые четыре из них были известны уже давно:

,

,

и

.
Мерсенн утверждал, что значение

будет простым для простых чисел

, принадлежащих множеству

. Во всем ли он был прав, можно проверить с помощью функции
Wolfram Language —
PrimeQ, в которой используются современные методы тестирования чисел на простоту, для которых не требуется поиска конкретного множителя, чтобы доказать, что число составное.

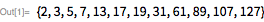
Вполне возможно, что его утверждение о том, что

— простое число, просто опечатка, и на самом деле он имел в виду

. Несложно понять, что проверка на простоту была при жизни Мерсенна делом затруднительным, поскольку проверка делением была одним из немногих доступных инструментов. Например, для

наименьшим множителем оказывается 15-значное число, так что даже с современными методами факторизации его не так-то легко найти. В функции
FactorInteger используются
наиболее совершенные методы, которые позволяют применять метод факторизации в отношении больших целых чисел.
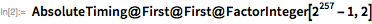

Теорема множителей Эйлера и Мерсенна
Первые важные достижения в области проверки на простоту принадлежат великому математику
Леонарду Эйлеру, который незадолго до 1772 года уточнил, что

является простым. Он сделал это, продемонстрировав, что любой простой делитель

должен быть равен 1 или 62 (mod 248).


Такой относительно короткий список даже во времена Эйлера мог быть проверен с помощью пробного деления (вручную). Ему принадлежит применение
теоремы Мерсенна, в которой говорится, что если

является делителем

, то

,

и

для некоторого целого положительного числа

. Эти факты значительно ограничивают количество возможных делителей

. С помощью функций, представленных ниже, демонстрируется использование этой теоремы с целью предоставления списка возможных делителей

, меньших, чем

.
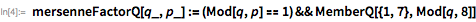
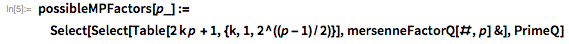


Мы используем эти функции, чтобы быстро найти делитель

. Обратите внимание, что

является делителем

тогда и только тогда, когда

. Это дает возможность использовать функцию
PowerMod, что обеспечивает эффективное возведение в степень по модулю.

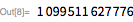





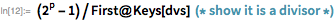

Ниже приводится число Мерсенна с 161649 знаками:.

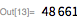
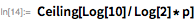



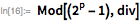

Люка и Лемер
Следующим важным шагом стало открытие
Эдуардом Люка метода для проверки простоты чисел данной формы. Он использовал свой метод в 1876 году для проверки, является ли

(самое большое число Мерсенна "докомпьютерной" эпохи) простым. В начале двадцатого века, когда основы двоичной арифметики и алгебры стали широко известны,
Дерек Генри Лемер усовершенствовал метод Люка. Полученный в результате тест
простоты чисел Люка-Лемера обеспечивал эффективную проверку, если число данной формы являлось простым. Проверка проводилась с помощью сравнения по модулю:

Это означает, что

идентично числу, представленному его

битами низшего порядка, плюс — числами, представленными остальными битами. Это соотношение может применяться рекурсивно до тех пор, пока

.
Рассмотрим следующий пример. Здесь мы покажем, что

для

. Обратите внимание, что

(23 бита низшего порядка) и

— означает, что остальные биты сдвинуты в крайнее нижнее положение.
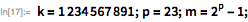


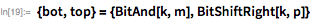


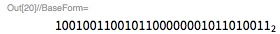




Функция ниже задает этот метод для вычисления

с использованием только битовых операций (без деления). Обратите внимание на то, что

имеет двоичную форму

, при этом нет ни одного 0, и поэтому она также служит в качестве маски для

битов низшего порядка числа

.

Следующая функция реализует тест простоты Люка-Лемера (LLT). Определим последовательность

,

. Тогда

является простым тогда и только тогда, когда

.

Опыт показывает, что основное время выполнения этих функций тратится на целочисленную арифметику.
Чтобы проверить, является ли

простым, лучше сначала проверять простоту на небольших простых делителях и выполнять другие проверки простоты. Сначала мы используем теорему делителей простых чисел Мерсенна, закодированную в
checkMPDivisors, а затем функцию
PrimeQ. Если это не сработает, применим тест Люка-Лемера.

Здесь мы представляем расширенную версию функции
PrimeQ, которая применяет тест Люка-Лемера для больших чисел вида

.

От  до
до 
Первым простым числом Мерсенна, обнаруженным на компьютере с помощью теста Люка-Лемера, стало

, найденное Рафаэлем Робинсоном 30 января 1952 года на базе лампового компьютера SWAC (Standards Western Automatic Computer). Ниже вы видите блок памяти этого компьютера, содержащий 256 слов по 37 бит каждое.

20-е простое число Мерсенна было обнаружено
Александром Гурвицем в ноябре 1961 года в результате проведения 50-минутного теста Люка-Лемера на IBM 7090. Ниже мы воспроизводим эти результаты (на это потребовалось около 151 секунд машинного времени на современном одноядерном ноутбуке).




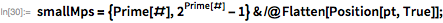


Одной из особенностей Wolfram Language, делающей его пригодным для такого рода работы, является его быстрая целочисленная арифметика. Поиск простых чисел Мерсенна стал настоящим вызовом на рассвете эпохи компьютеризированного поиска. Исследователи адаптировали методы быстрого преобразования Фурье для преобразования задачи умножения двух больших целых чисел в простое поэлементное произведение трансформированных цифр. Быстрое умножение целых чисел необходимо для шага возведения в квадрат в тесте Люка-Лемера. В Wolfram Language используются новейшие алгоритмы, оптимизированые для работы с точными целыми числами с миллиардами символов. Например, убедимся, что последнее из них, —

, — на самом деле простое число Мерсенна, и продемонстрируем все его цифры.



Совершенные числа
Существует интересная связь между простыми числами Мерсенна и совершенными числами.
Совершенное число — это число, равное сумме всех своих делителей (отличных от самого числа). Евклид предполагал, а Эйлер доказал, что все четные совершенные числа, имеют вид

. Функция Wolfram Language
PerfectNumberQ проверяет, является ли число совершенным. Продемонстрируем это свойство на

.




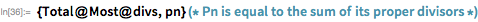



21-е, 22-е и 23-е числа Мерсенна
Перейдем к переоткрытию 21-го, 22-го и 23-го чисел Мерсенна (будем обозначать их далее в форме вида

):

,

,

. Все они были обнаружены Дональдом Гиллисом, который запускал LLT на ILLIAC II всю весну 1963 года (см.
здесь). Для проверки всех чисел вида

для простых чисел в промежутке

нам понадобилось около 6 минут.


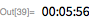

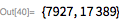

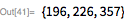




24-е, 25-е и 26-е числа Мерсенна
Далее мы расширяем поиск, чтобы найти

,

,

. Последнее из них было обнаружено в феврале 1979 г. Лэндоном Куртом Ноллом и Лорой Никель. Они искали в диапазоне от

до

на суперкомпьютере CDC Cyber 174 (почитать об этом можно
здесь). Наши расчеты становятся более долгими, так что мы начинаем использовать параллельную обработку. Поскольку тесты независимы, для ускорения работы мы можем использовать
ParallelMap. Проверка диапазона

занимает приблизительно три с половиной минуты (используются 4 ядра).



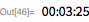



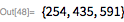
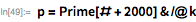
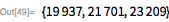
Обратите внимание на то, что специализированный тест Люка-Лемера значительно быстрее, чем более общая функция
PrimeQ (для данных чисел Мерсенна).




27-е и 28-е числа Мерсенна
Далее мы проверили диапазон

, чтобы найти число

. Оно было обнаружено в апреле 1979 года Гарри Нельсоном и его командой (они использовали суперкомпьютер Cray-1). Наш поиск завершился за 15 минут.






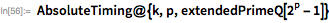
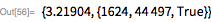
Следующее число Мерсенна,

. Оно был открыто в сентябре 1982 года Дэвидом Словински — также на Cray-1. Этот суперкомпьютер весил около 5 тонн и потреблял около 115 киловатт электроэнергии, а его вычислительная производительность достигала 160
мегафлопс. Он поставлялся с 1 миллионом 64-разрядных слов памяти (8 мегабайт), а стоил около 16000000$ в сегодняшних ценах. Ниже показана деталь его системы охлаждения. Для сравнения:
Raspberry Pi весит несколько унций, работает на 4 Вт, обеспечивает около 410 мегафлопс и снабжен 1Гб оперативной памяти, и это все — за 40$. А еще он поставляется сразу с системой
Mathematica.


Число

содержит 25962 цифры. Это значение мы нашли за 1 час и 14 минут (на моем ноутбуке, а не на Raspberry Pi), проводя испытания в диапазоне

.




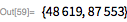

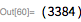

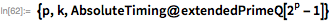

29-е число Мерсенна
Поскольку теперь нам требуется более серьезное компьютерное время, мы также производим отметку времени для каждого прогона. Теперь мы проверяем диапазон

. Через 1 час и 44 минут компьютер показал:

. Это число впервые было обнаружено 29 января 1988 года Уокер Колкуиттом и Люком Уэлшем (суперкомпьютер NEC DX-2; статью можно найти
здесь).







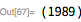
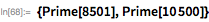
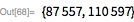





30-е и 31-е числа Мерсенна
Следующие два простых числа Мерсенна:

и

, — были на самом деле обнаружены еще до 29-го (той же командой, которая обнаружила и 28-е). Они использовали Cray X-MP, чтобы найти 30-е число Мерсенна в сентябре 1983 года и 31-е — в сентябре 1985 года. Проверим

с помощью функции поиска в диапазоне

. Для проверки каждого

в этом диапазоне понадобилось 4 часа и 8 минут.









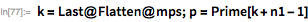
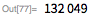
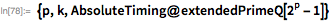



Великий интернет-поиск чисел Мерсенна
С открытием 34-го простого числа Мерсенна —

— в сентябре 1996 года закончилась эпоха суперкомпьютеров для поиска простых чисел Мерсенна. Следующие 15 были найдены добровольцами Великого интернет-поиска простых чисел Мерсенна (
GIMPS), в рамках которого проводится вариант теста Люка-Лемера (в качестве фонового процесса) на персональных компьютерах. Этот масштабный проект распределенных вычислений в настоящее время достигает уровня производительности, эквивалентного приблизительно 300 терафлопс в секунду, причем задействуется время простоя более чем 1,3 миллиона компьютеров.

Проверим 34-е число Мерсенна с помощью теста Люка-Лемера. На этом этапе мы достигли предела возможностей личного компьютера. На тестирование тысячи чисел Мерсенна в этом диапазоне потребуется много дней. Интересно отметить, что тест Люка-Лемера часто используется в качестве
стресс-теста надежности компьютерного оборудования и программного обеспечения, так как даже одна арифметическая ошибка среди миллиардов вычислений, необходимых для тестирования одного большого простого числа, повлечет за собой неправильный вывод, что будет означать потерю числа Мерсенна или ложный ответ. Тот факт, что мы проверили каждое

для простых чисел в промежутке между 2 и 139901, убедительно доказывает надежность арифметики больших чисел и бинарных операций в системе Mathematica и языке Wolfram Language.


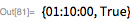
Факторизация чисел Мерсенна
Как мы уже видели, количество возможных множителей в разложении чисел вида

согласно теореме множителей Мерсенна ограниченно. Это позволило провести эффективный компьютеризированный поиск делителей больших чисел этой формы. На момент написания этой статьи все числа Мерсенна (до

) были полностью разложены на множители (иллюстрации можно найти
здесь). Проект GIMPS также привел к открытию крупных множителей многих чисел Мерсенна в качестве побочного продукта проверки простоты чисел. Новую статью, которая представляет собой современный подход к решению этой проблемы (наряду с 17 новыми факторизациями), можно найти
здесь. Наибольшее факторизованное число составило

; его наименьший из найденных делителей имеет 76 десятичных цифр. Его наименьший делитель равен 23. Общее время, необходимое для того, чтобы получить этот результат составляет 7500 лет (речь о компьютерном времени).
Мы можем быстро найти несколько первых множителей

с помощью функции
FactorInteger.
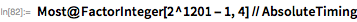

Все простые числа Мерсенна, обнаруженные на сегодняшний день, каталогизированы в Wolfram Language (до 44-го). Доступ к этой информации обеспечивается функциями
MersennePrimeExponent и
MersennePrimeExponentQ.




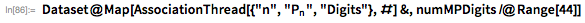

Если вас заинтересовала эта тема, вы можете найти более подробную информацию на следующих веб-сайтах:



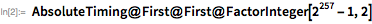

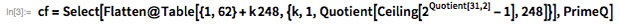

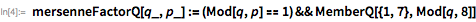
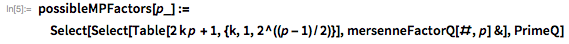


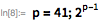
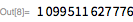


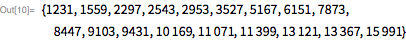

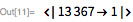
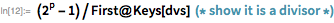
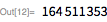


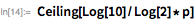


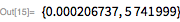
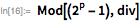


 для
для  (23 бита низшего порядка) и
(23 бита низшего порядка) и  — означает, что остальные биты сдвинуты в крайнее нижнее положение.
— означает, что остальные биты сдвинуты в крайнее нижнее положение.

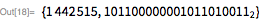
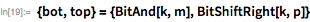



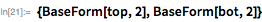
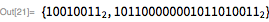

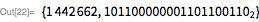




 до
до