В ресторане заиграла почти забытая песня. Вы слушали её в далёком прошлом. Сколько трогательных воспоминаний способны вызвать аккорды и слова… Вы отчаянно хотите послушать эту песню снова, но вот её название напрочь вылетело из головы! Как быть? К счастью, в нашем фантастическом высокотехнологичном мире есть ответ на этот вопрос.
У вас в кармане лежит смартфон, на котором установлена программа для распознавания музыкальных произведений. Эта программа – ваш спаситель. Для того чтобы узнать название песни, не придётся ходить из угла в угол в попытках выудить из собственной памяти заветную строчку. И ведь не факт, что это получится. Программа, если дать ей «послушать» музыку, тут же сообщит название композиции. После этого можно будет слушать милые сердцу звуки снова и снова. До тех пор, пока они не станут с вами единым целым, или – до тех пор, пока вам всё это не надоест.
Мобильные технологии и невероятный прогресс в области обработки звука дают разработчикам алгоритмов возможность создавать приложения для распознавания музыкальных произведений. Одно из самых популярных решений такого рода называется Shazam. Если дать ему 20 секунд звучания, неважно, будет ли это кусок вступления, припева или часть основного мотива, Shazam создаст сигнатурный код, сверится с базой данных и воспользуется собственным алгоритмом распознавания музыки для того, чтобы выдать название произведения.
Как же всё это работает?
Описание базового алгоритма Shazam в 2003-м году опубликовал его создатель, Эвери Ли Чунь Вонг (Avery Li-Chung Wang). В данном материале мы в деталях разберём основы алгоритма распознавания музыки Shazam.
Что такое, на самом деле, звук? Может быть, это некая таинственная бестелесная субстанция, которая проникает в наши уши и позволяет слышать?
Конечно же, всё не так уж и загадочно. Давно известно, то звук – это механические колебания, которые распространяются в твёрдых, жидких и газообразных средах в форме упругих волн. Когда волна достигает уха, в частности – барабанной перепонки, приводятся в движение слуховые косточки, которые передают колебания дальше, к волосковым клеткам, расположенным во внутреннем ухе. В результате механические колебания преобразуются в электрические импульсы, которые передаются по слуховым нервам в мозг.
Устройства для записи звука довольно точно имитируют вышеописанный процесс, конвертируя давление звуковой волны в электрический сигнал. Звуковая волна в воздухе – это непрерывный сигнал, представленный областями сжатия и разрежения. Микрофон, первый электронный компонент, с которым встречается звуковой сигнал, преобразует его в сигнал электрический, который всё ещё остаётся непрерывным. Подобные сигналы в цифровом мире не особо полезны, поэтому, перед хранением и обработкой в цифровых системах, их нужно преобразовать в дискретную форму. Делается это с помощью выборки значений, представляющих значения амплитуды сигнала.
В процессе подобного преобразования производится квантование аналогового сигнала. Здесь не обходится без небольшого количества ошибок. Таким образом, мы имеем дело не с одномоментным преобразованием, аналого-цифровой преобразователь выполняет множество операций по преобразованию очень маленьких частей аналогового сигнала в цифровой. Этот процесс называют дискретизацией или сэмплингом.
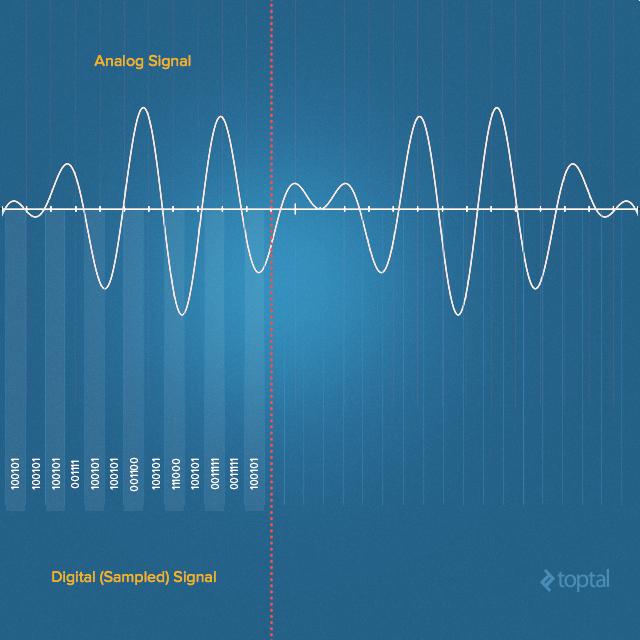
Аналоговый (непрерывный) и цифровой (дискретный) сигналы
Благодаря теореме Котельникова мы знаем, какая частота дискретизации нужна для того, чтобы точно представить непрерывный сигнал, ограниченный некоторой частотой. В частности, для того, чтобы захватить весь частотный спектр звуков, доступных человеческому слуху, мы должны использовать частоту дискретизации, вдвое превышающую верхнюю границу частот, слышимых человеком.
А именно, человек может слышать звуки в диапазоне примерно от 20 Гц до 20000 Гц. В результате звук чаще всего записывают с частотой дискретизации 44100 Гц. Именно эта частота дискретизации используется в компакт-дисках. Она же чаще всего применяется для кодирования звука в группе стандартов MPEG-1 (VCD, SVCD, MP3).
Широкому использованию частоты дискретизации в 44100 Гц мы обязаны, преимущественно, корпорации Sony. В своё время звуковые дорожки, закодированные таким способом, удобно было совмещать с видео в стандартах PAL (25 кадров в секунду) и NTSC (30 кадров в секунду), работать с ними, используя существующее оборудование. Весьма важно и то, что эта частота достаточна для качественной передачи звука в диапазоне до 20000 Гц. Цифровое звуковое оборудование, использующее эту частоту дискретизации, вполне соответствовало по качеству аналоговому оборудованию тех времён, когда происходило становление стандартов цифрового звука. В итоге, выбирая частоту дискретизации звука при записи, вы, вероятнее всего, остановитесь на 44100 Гц.
Записать сэмплированный звуковой сигнал – задача довольно простая. Современные звуковые карты содержат встроенные аналого-цифровые преобразователи. Поэтому достаточно выбрать язык программирования, найти подходящую библиотеку для работы со звуком, указать частоту дискретизации, количество каналов (обычно – один или два, для монофонического и стереофонического звучания, соответственно), выбрать количество битов в одном сэмпле (например, часто используется 16 бит). Затем нужно открыть строку данных со звуковой карты, так же, как открывается любой входной поток, и записать его содержимое в байтовый массив. Вот, как это делается в Java:
Теперь достаточно прочесть данные из объекта класса
В нашем массиве записано цифровое представление звукового сигнала во временной области. То есть, у нас есть сведения о том, как менялась амплитуда сигнала с течением времени.
В 19 веке Жан Батист Джозеф Фурье сделал выдающееся открытие. Заключается оно в том, что любой сигнал во временной области эквивалентен сумме некоторого количества (возможно, бесконечного) простых синусоидальных сигналов, при условии, что каждая синусоида имеет определённую частоту, амплитуду и фазу. Набор синусоид, которые формируют исходный сигнал, называют рядом Фурье.
Другими словами, можно представить практически любой сигнал, развёрнутый во времени, просто задав набор частот, амплитуд и фаз, соответствующих каждой из синусоид, которые этот сигнал формируют. Такое представление сигналов называют набором частотных интервалов. В каком-то смысле, сведения о частотных интервалах являются чем-то вроде «отпечатков пальцев» или сигнатур сигналов, развёрнутых во времени, давая нам статическое представление динамических данных.
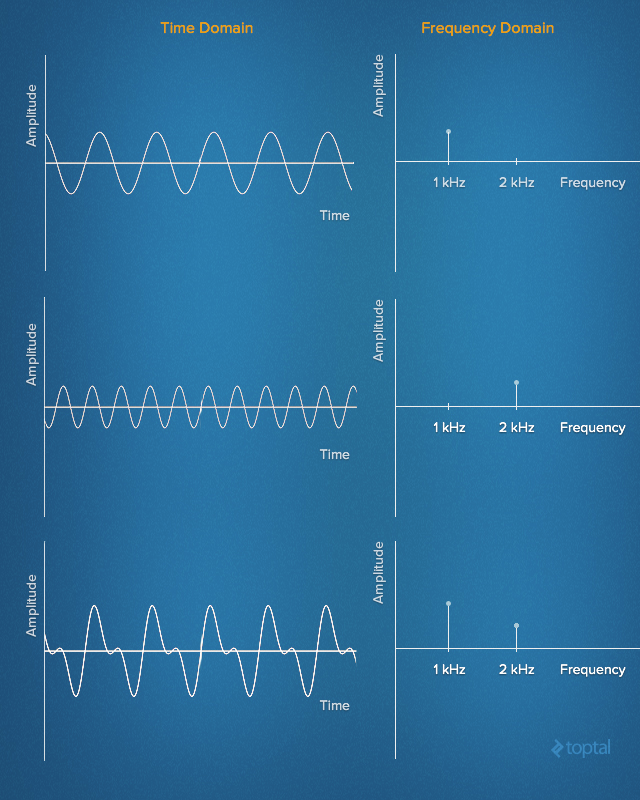
Сигналы, развёрнутые во времени, и их частотные характеристики
Вот как выглядит анимированное представление Ряда Фурье для прямоугольной волны частотой 1 Гц. Здесь же показана аппроксимация исходного сигнала на основе набора синусоид. На верхнем графике сигнал показан в амплитудно-временной области, на нижнем дано его представление в амплитудно-частотном виде.
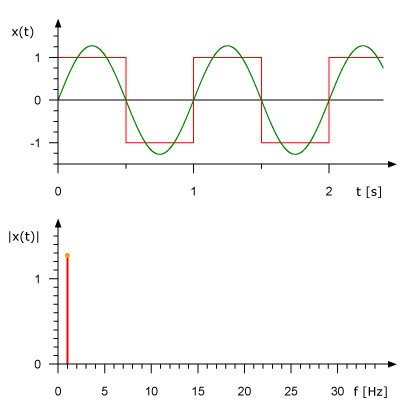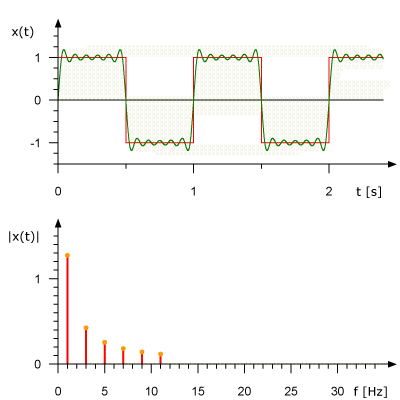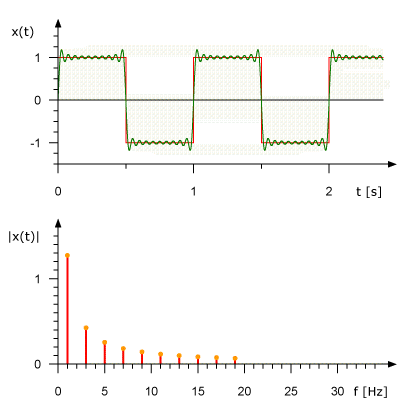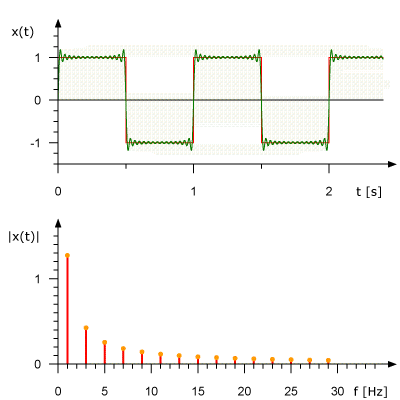
Преобразование Фурье в действии. Источник: Rene Schwarz
Анализ частотных характеристик сигналов значительно облегчает решение множества задач. Оперировать такими характеристиками в сфере обработки цифровых сигналов, очень удобно. Они позволяют изучать спектр сигнала (его частотные характеристики), определять, какие частоты в этом сигнале имеются, а какие – нет. После этого можно произвести фильтрацию, усилить или ослабить некоторые частоты, или просто распознать звук определённой высоты среди имеющегося набора частот.
Итак, нужно найти способ получения частотных характеристик сигналов, развёрнутых во времени. В этом нам поможет дискретное преобразование Фурье (ДПФ, DFT, Discrete Fourier Transform). ДПФ – это математический метод анализа Фурье для дискретных сигналов. С его помощью можно преобразовать конечный набор образцов сигнала, взятых с равными промежутками времени, в список коэффициентов конечной комбинации комплексных синусоид, упорядоченных по частоте, принимая во внимание, что эти синусоиды были дисретизированы с одной и той же частотой.
Один из самых популярных численных алгоритмов для вычисления ДПФ называется быстрое преобразование Фурье (БПФ, FFT, Fast Fourier Transformation). На самом деле, БПФ представлен целым набором алгоритмов. Среди них чаще всего используются варианты алгоритма Кули-Тьюки (Cooley-Tukey). В основе этого алгоритма лежит принцип «разделяй и властвуй». В ходе вычислений используется рекурсивное разложение исходного ДПФ на мелкие части. Прямое вычисление ДПФ для некоторого набора данных n требует O(n2) операций, а использование алгоритма Кули-Тьюки позволяет решить ту же задачу за O(n log n) операций.
Несложно найти подходящую библиотеку, реализующую алгоритм БПФ. Вот несколько таких библиотек для разных языков:
Вот пример функции для вычисления БПФ, написанной на Java. На её вход подаются комплексные числа. Для того чтобы разобраться с взаимоотношениями между комплексными числами и тригонометрическими функциями, полезно почитать о формуле Эйлера.
Вот пример сигнала до и после БПФ-анализа.
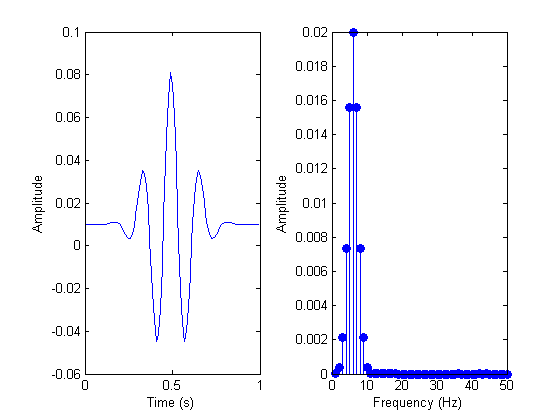
Сигнал до и после БПФ-анализа
Один из неприятных побочных эффектов БПФ заключается в том, что проведя анализ, мы теряем информацию о времени. (Хотя, теоретически, подобного можно избежать, но на практике для этого понадобится огромная вычислительная мощность.) Например, для трёхминутной песни мы можем видеть звуковые частоты и их амплитуды, но вот где именно в произведении эти частоты встречаются, не знаем. А это – важнейшая характеристика, которая делает музыкальное произведение тем, что оно есть! Нам нужно как-то узнать точные значения времени, когда появляется каждая из частот.
Именно поэтому мы будем пользоваться чем-то вроде скользящего окна, или блока данных, и подвергать трансформации лишь ту часть сигнала, которая в это «окно» попадает. Размер каждого блока можно определить с использованием различных подходов. Например, если мы записываем двухканальный звук с размером образца равным 16 бит и с частотой дискретизации 44100 Гц, одна секунда такого звука займёт 176 Кб памяти (44100 образцов * 2 байта * 2 канала). Если мы установим размер скользящего окна, равный 4 Кб, то каждую секунду нам нужно будет проанализировать 44 блока данных. Это – довольно высокое разрешение для детального анализа композиции.
Вернёмся к программированию.
Во внутреннем цикле мы помещаем данные из временной области (образцы звука) в комплексные числа с мнимой частью равной 0. Во внешнем цикле проходим по всем блокам данных и для каждого из них запускаем БПФ-анализ.
Как только у нас будут сведения о частотных характеристиках сигнала, можно приступать к формированию цифровой сигнатуры музыкального произведения. Это – самая важная часть всего процесса распознавания музыки, который реализует Shazam. Главная сложность здесь – выбрать из огромного количества частот именно те, которые важнее всего. Чисто интуитивно мы обращаем внимание на частоты с максимальными амплитудами (обычно их называют пиками).
Однако, в одной песне диапазон «сильных» частот может варьироваться, скажем, от ноты «до» контроктавы (32,70 Гц), до ноты «до» пятой октавы (4186,01 Гц). Это – огромный интервал. Поэтому, вместо того, чтобы за сразу проанализировать весь частотный диапазон, мы можем выбрать несколько более мелких интервалов. Выбор можно сделать, основываясь на частотах, которые обычно присущи важным музыкальным компонентам, и проанализировать их по отдельности. Например, можно воспользоваться интервалами, которые вот этот программист использовал для своей реализации алгоритма Shazam. А именно, это 30 Гц – 40 Гц, 40 Гц – 80 Гц и 80 Гц – 120 Гц для низких звуков (сюда попадает, например, бас-гитара). Для средних и более высоких звуков применяются частоты 120 Гц – 180 Гц и 180 Гц – 300 Гц (сюда входит вокал и большинство других инструментов).
Теперь, когда мы определились с интервалами, можно просто найти в них частоты с самыми высокими уровнями. Эти сведения и формируют сигнатуру для конкретного анализируемого блока данных, а она, в свою очередь, является частью сигнатуры всей песни.
Заметьте, что мы должны учитывать то, что запись выполнена не в идеальных условиях (то есть, не в звукоизолированном помещении). Как результат, надо предусмотреть наличие в записи посторонних шумов и возможное искажение записываемого звука, зависящее от характеристик помещения. К этому вопросу стоит подойти очень серьёзно, в реальных системах стоит реализовать настройку анализа возможных искажений и посторонних звуков (fuzz factor) в зависимости от условий, в которых проводится запись.
Для упрощения поиска музыкальных композиций их сигнатуры используются как ключи в хэш-таблице. Ключам соответствуют значения времени, когда набор частот, для которых найдена сигнатура, появился в произведении, и идентификатор самого произведения (название песни и имя исполнителя, например). Вот вариант того, как подобные записи могут выглядеть в базе данных.
Если обработать таким способом некую библиотеку музыкальных записей, можно будет построить базу данных с полными сигнатурами каждого произведения.
Для того чтобы выяснить, какая же песня играет сейчас в ресторане, надо записать звук с помощью телефона и прогнать его через вышеописанный процесс вычисления сигнатур. Затем можно запустить поиск вычисленных хэш-тегов в базе данных.
Но не всё так просто. Дело в том, что у многих фрагментов различных произведений хэш-тэги совпадают. Например, может оказаться так, что какой-то фрагмент песни A звучит точно так же, как некий участок песни E. И тут нет ничего удивительного. Музыканты и композиторы постоянно «заимствуют» друг у друга удачные музыкальные фигуры.
Всякий раз, когда удаётся обнаружить совпадающий хэш-тег, число возможных совпадений уменьшается, но весьма вероятно, что только лишь эти сведения не позволят нам настолько сузить диапазон поиска, чтобы остановиться на единственной правильной песне. Поэтому в алгоритме распознавания музыкальных произведений нам нужно проверять ещё кое-что. А именно – речь идёт об отметках времени.
Тот фрагмент песни, что записали в ресторане, может быть из любого её места, поэтому мы просто не в состоянии напрямую сравнивать относительное время внутри записанного фрагмента с тем, что есть в базе данных.
Однако если найдено несколько совпадений, можно проанализировать относительный тайминг совпадений, и, таким образом, повысить достоверность поиска.
Например, если взглянуть в вышеприведенную таблицу, можно обнаружить, что хэш-тег 30 51 99 121 195 относится и к песне A, и к песне E. Если секундой спустя мы будем проверять хэш-тег 34 57 95 111 200, то обнаружим ещё одно совпадение с песней A, к тому же, в подобном случаем мы будем знать о том, что совпадают и хэш-теги и их распределение во времени.
Пусть i1 и i2 – это отметки времени в записанной песне, j1 и j2 – отметки времени в песне из базы данных. Мы можем говорить о том, что имеются два совпадения, с учётом совпадения разницы во времени, если выполняется следующее условие:
Это даёт возможность не заботиться о том, на какую именно часть песни приходится запись: на начало, середину, или на самый конец.
И, наконец, маловероятно, что каждый обработанный фрагмент записанной в «диких» условиях песни совпадёт с аналогичным фрагментом из базы данных, построенной на основе студийных записей. Запись, на основе которой мы хотим найти название произведения, будет включать в себя много шума, что приведёт к неким расхождениям при сравнении. Поэтому, вместо того, чтобы пытаться исключить из списка совпадений всё, кроме единственной верной композиции, в конце процедуры сопоставления с базой данных мы отсортируем записи, в которых нашлись совпадения. Сортировать будем в убывающем порядке. Чем больше совпадений – тем вероятнее то, что мы нашли нужную композицию. Соответственно, она окажется на вершине списка.
Вот обзор всей процедуры распознавания музыкальных композиций. Пройдёмся по нему от начала до конца.
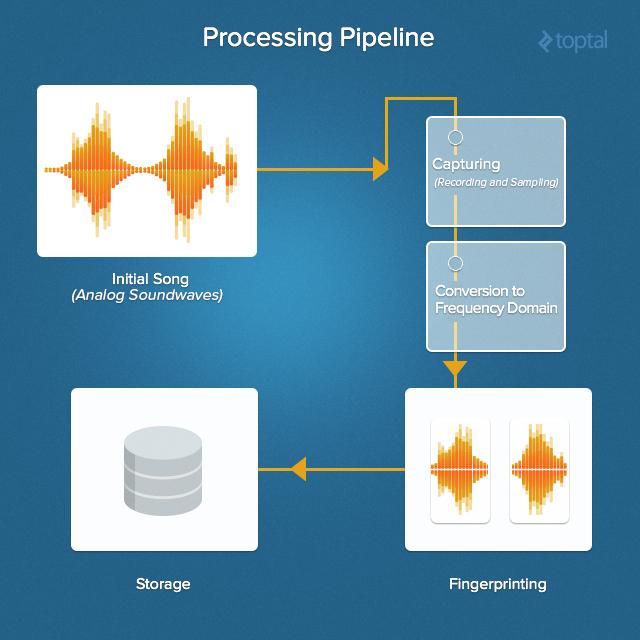
Обзор процедуры распознавания музыки
Всё начинается с исходного звука. Потом его захватывают, находят частотные характеристики, вычисляют хэш-теги и сравнивают их с теми, что хранятся в музыкальной базе данных.
В подобных системах базы данных могут быть просто огромными, поэтому важно использовать решения, которые поддаются масштабированию. В связях таблиц баз данных особенной нужды нет, модель данных очень проста, поэтому здесь вполне подойдёт какая-нибудь разновидность NoSQL-базы данных.
Программы, подобные той, о которой мы здесь говорили, подходят для поиска схожих мест в музыкальных произведениях. Теперь, когда вы понимаете, как работает Shazam, вы можете увидеть, что алгоритмы распознавания музыки применимы не только в роли «напоминалок» названий забытых песен из прошлого, звучащих по радио в такси.
Например, с их помощью можно искать музыкальный плагиат, или задействовать их для того, чтобы найти исполнителей, которые вдохновляли некоторых первопроходцев в блюзе, джазе, в рок-музыке, в поп-музыке, да в любом другом жанре.
Возможно, хорошим экспериментом станет заполнение базы данных классикой – сочинениями Баха, Бетховена, Вивальди, Вагнера, Шопена и Моцарта и поиск схожего в их работах. Так вполне можно выяснить, что даже Боб Дилан, Элвис Пресли и Роберт Джонсон не прочь были что-нибудь позаимствовать у других!
Но можем ли мы их за это винить? Уверен, что нет. Ведь музыка – это всего лишь звуковая волна, которую человек слышит, запоминает и повторяет у себя в голове. Там она развивается, меняется – до тех пор, пока её не запишут в студии и не выпустят на волю, где она вполне может вдохновить очередного гения от музыки.
У вас в кармане лежит смартфон, на котором установлена программа для распознавания музыкальных произведений. Эта программа – ваш спаситель. Для того чтобы узнать название песни, не придётся ходить из угла в угол в попытках выудить из собственной памяти заветную строчку. И ведь не факт, что это получится. Программа, если дать ей «послушать» музыку, тут же сообщит название композиции. После этого можно будет слушать милые сердцу звуки снова и снова. До тех пор, пока они не станут с вами единым целым, или – до тех пор, пока вам всё это не надоест.
Мобильные технологии и невероятный прогресс в области обработки звука дают разработчикам алгоритмов возможность создавать приложения для распознавания музыкальных произведений. Одно из самых популярных решений такого рода называется Shazam. Если дать ему 20 секунд звучания, неважно, будет ли это кусок вступления, припева или часть основного мотива, Shazam создаст сигнатурный код, сверится с базой данных и воспользуется собственным алгоритмом распознавания музыки для того, чтобы выдать название произведения.
Как же всё это работает?
Описание базового алгоритма Shazam в 2003-м году опубликовал его создатель, Эвери Ли Чунь Вонг (Avery Li-Chung Wang). В данном материале мы в деталях разберём основы алгоритма распознавания музыки Shazam.
От аналоговых сигналов к цифровым: дискретизация
Что такое, на самом деле, звук? Может быть, это некая таинственная бестелесная субстанция, которая проникает в наши уши и позволяет слышать?
Конечно же, всё не так уж и загадочно. Давно известно, то звук – это механические колебания, которые распространяются в твёрдых, жидких и газообразных средах в форме упругих волн. Когда волна достигает уха, в частности – барабанной перепонки, приводятся в движение слуховые косточки, которые передают колебания дальше, к волосковым клеткам, расположенным во внутреннем ухе. В результате механические колебания преобразуются в электрические импульсы, которые передаются по слуховым нервам в мозг.
Устройства для записи звука довольно точно имитируют вышеописанный процесс, конвертируя давление звуковой волны в электрический сигнал. Звуковая волна в воздухе – это непрерывный сигнал, представленный областями сжатия и разрежения. Микрофон, первый электронный компонент, с которым встречается звуковой сигнал, преобразует его в сигнал электрический, который всё ещё остаётся непрерывным. Подобные сигналы в цифровом мире не особо полезны, поэтому, перед хранением и обработкой в цифровых системах, их нужно преобразовать в дискретную форму. Делается это с помощью выборки значений, представляющих значения амплитуды сигнала.
В процессе подобного преобразования производится квантование аналогового сигнала. Здесь не обходится без небольшого количества ошибок. Таким образом, мы имеем дело не с одномоментным преобразованием, аналого-цифровой преобразователь выполняет множество операций по преобразованию очень маленьких частей аналогового сигнала в цифровой. Этот процесс называют дискретизацией или сэмплингом.
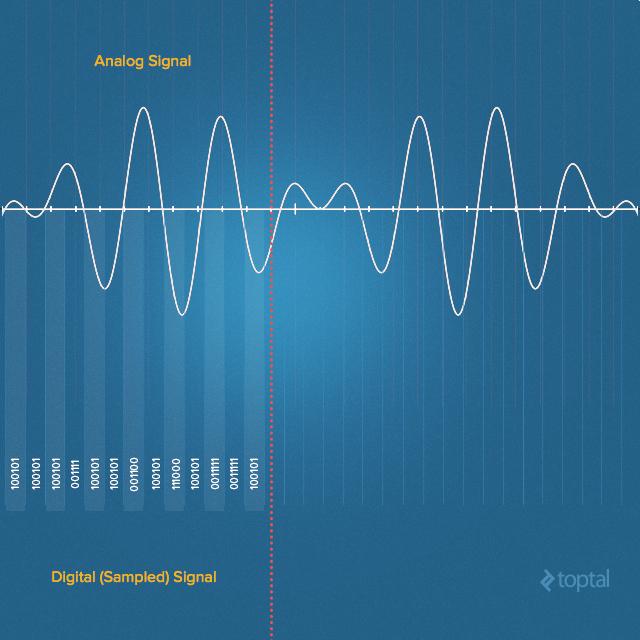
Аналоговый (непрерывный) и цифровой (дискретный) сигналы
Благодаря теореме Котельникова мы знаем, какая частота дискретизации нужна для того, чтобы точно представить непрерывный сигнал, ограниченный некоторой частотой. В частности, для того, чтобы захватить весь частотный спектр звуков, доступных человеческому слуху, мы должны использовать частоту дискретизации, вдвое превышающую верхнюю границу частот, слышимых человеком.
А именно, человек может слышать звуки в диапазоне примерно от 20 Гц до 20000 Гц. В результате звук чаще всего записывают с частотой дискретизации 44100 Гц. Именно эта частота дискретизации используется в компакт-дисках. Она же чаще всего применяется для кодирования звука в группе стандартов MPEG-1 (VCD, SVCD, MP3).
Широкому использованию частоты дискретизации в 44100 Гц мы обязаны, преимущественно, корпорации Sony. В своё время звуковые дорожки, закодированные таким способом, удобно было совмещать с видео в стандартах PAL (25 кадров в секунду) и NTSC (30 кадров в секунду), работать с ними, используя существующее оборудование. Весьма важно и то, что эта частота достаточна для качественной передачи звука в диапазоне до 20000 Гц. Цифровое звуковое оборудование, использующее эту частоту дискретизации, вполне соответствовало по качеству аналоговому оборудованию тех времён, когда происходило становление стандартов цифрового звука. В итоге, выбирая частоту дискретизации звука при записи, вы, вероятнее всего, остановитесь на 44100 Гц.
Запись: захват звука
Записать сэмплированный звуковой сигнал – задача довольно простая. Современные звуковые карты содержат встроенные аналого-цифровые преобразователи. Поэтому достаточно выбрать язык программирования, найти подходящую библиотеку для работы со звуком, указать частоту дискретизации, количество каналов (обычно – один или два, для монофонического и стереофонического звучания, соответственно), выбрать количество битов в одном сэмпле (например, часто используется 16 бит). Затем нужно открыть строку данных со звуковой карты, так же, как открывается любой входной поток, и записать его содержимое в байтовый массив. Вот, как это делается в Java:
private AudioFormat getFormat() {
float sampleRate = 44100;
int sampleSizeInBits = 16;
int channels = 1; //Монофонический звук
boolean signed = true; //Флаг указывает на то, используются ли числа со знаком или без
boolean bigEndian = true; //Флаг указывает на то, следует ли использовать обратный (big-endian) или прямой (little-endian) порядок байтов return new AudioFormat(sampleRate, sampleSizeInBits, channels, signed, bigEndian);
}
final AudioFormat format = getFormat(); //Заполнить объект класса AudioFormat параметрами
DataLine.Info info = new DataLine.Info(TargetDataLine.class, format);
final TargetDataLine line = (TargetDataLine) AudioSystem.getLine(info);
line.open(format);
line.start();Теперь достаточно прочесть данные из объекта класса
TargetDataLine. В примере используется флаг running, это глобальная переменная, на которую возможно воздействие из другого потока. Например, подобная переменная позволит нам остановить захват звука из потока пользовательского интерфейса с помощью кнопки «Стоп».OutputStream out = new ByteArrayOutputStream();
running = true;
try {
while (running) {
int count = line.read(buffer, 0, buffer.length);
if (count > 0) {
out.write(buffer, 0, count);
}
}
out.close();
} catch (IOException e) {
System.err.println("I/O problems: " + e);
System.exit(-1);
}Временная и частотная области
В нашем массиве записано цифровое представление звукового сигнала во временной области. То есть, у нас есть сведения о том, как менялась амплитуда сигнала с течением времени.
В 19 веке Жан Батист Джозеф Фурье сделал выдающееся открытие. Заключается оно в том, что любой сигнал во временной области эквивалентен сумме некоторого количества (возможно, бесконечного) простых синусоидальных сигналов, при условии, что каждая синусоида имеет определённую частоту, амплитуду и фазу. Набор синусоид, которые формируют исходный сигнал, называют рядом Фурье.
Другими словами, можно представить практически любой сигнал, развёрнутый во времени, просто задав набор частот, амплитуд и фаз, соответствующих каждой из синусоид, которые этот сигнал формируют. Такое представление сигналов называют набором частотных интервалов. В каком-то смысле, сведения о частотных интервалах являются чем-то вроде «отпечатков пальцев» или сигнатур сигналов, развёрнутых во времени, давая нам статическое представление динамических данных.
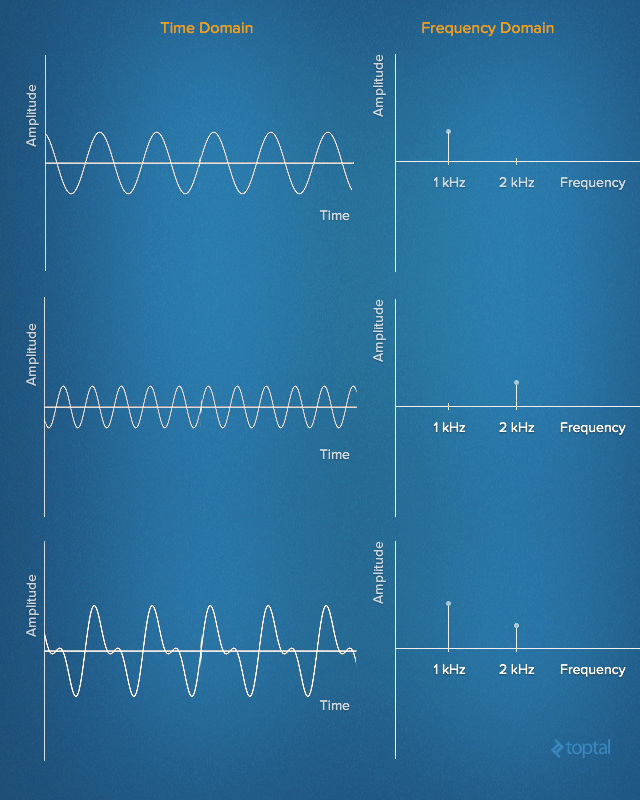
Сигналы, развёрнутые во времени, и их частотные характеристики
Вот как выглядит анимированное представление Ряда Фурье для прямоугольной волны частотой 1 Гц. Здесь же показана аппроксимация исходного сигнала на основе набора синусоид. На верхнем графике сигнал показан в амплитудно-временной области, на нижнем дано его представление в амплитудно-частотном виде.

Преобразование Фурье в действии. Источник: Rene Schwarz
Анализ частотных характеристик сигналов значительно облегчает решение множества задач. Оперировать такими характеристиками в сфере обработки цифровых сигналов, очень удобно. Они позволяют изучать спектр сигнала (его частотные характеристики), определять, какие частоты в этом сигнале имеются, а какие – нет. После этого можно произвести фильтрацию, усилить или ослабить некоторые частоты, или просто распознать звук определённой высоты среди имеющегося набора частот.
Дискретное преобразование Фурье
Итак, нужно найти способ получения частотных характеристик сигналов, развёрнутых во времени. В этом нам поможет дискретное преобразование Фурье (ДПФ, DFT, Discrete Fourier Transform). ДПФ – это математический метод анализа Фурье для дискретных сигналов. С его помощью можно преобразовать конечный набор образцов сигнала, взятых с равными промежутками времени, в список коэффициентов конечной комбинации комплексных синусоид, упорядоченных по частоте, принимая во внимание, что эти синусоиды были дисретизированы с одной и той же частотой.
Один из самых популярных численных алгоритмов для вычисления ДПФ называется быстрое преобразование Фурье (БПФ, FFT, Fast Fourier Transformation). На самом деле, БПФ представлен целым набором алгоритмов. Среди них чаще всего используются варианты алгоритма Кули-Тьюки (Cooley-Tukey). В основе этого алгоритма лежит принцип «разделяй и властвуй». В ходе вычислений используется рекурсивное разложение исходного ДПФ на мелкие части. Прямое вычисление ДПФ для некоторого набора данных n требует O(n2) операций, а использование алгоритма Кули-Тьюки позволяет решить ту же задачу за O(n log n) операций.
Несложно найти подходящую библиотеку, реализующую алгоритм БПФ. Вот несколько таких библиотек для разных языков:
- C – FFTW
- C++ – EigenFFT
- Java – JTransform
- Python – NumPy
- Ruby – Ruby-FFTW3 (интерфейс к FFTW)
Вот пример функции для вычисления БПФ, написанной на Java. На её вход подаются комплексные числа. Для того чтобы разобраться с взаимоотношениями между комплексными числами и тригонометрическими функциями, полезно почитать о формуле Эйлера.
public static Complex[] fft(Complex[] x) {
int N = x.length;
// fft чётных элементов
Complex[] even = new Complex[N / 2];
for (int k = 0; k < N / 2; k++) {
even[k] = x[2 * k];
}
Complex[] q = fft(even);
// fft нечетных элементов
Complex[] odd = even; // повторное использование массива
for (int k = 0; k < N / 2; k++) {
odd[k] = x[2 * k + 1];
}
Complex[] r = fft(odd);
// комбинируем
Complex[] y = new Complex[N];
for (int k = 0; k < N / 2; k++) {
double kth = -2 * k * Math.PI / N;
Complex wk = new Complex(Math.cos(kth), Math.sin(kth));
y[k] = q[k].plus(wk.times(r[k]));
y[k + N / 2] = q[k].minus(wk.times(r[k]));
}
return y;
}Вот пример сигнала до и после БПФ-анализа.
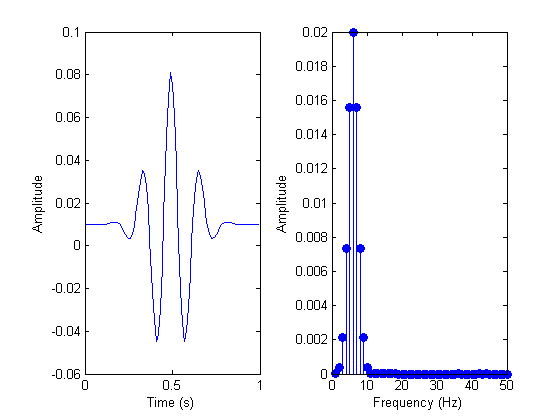
Сигнал до и после БПФ-анализа
Распознавание музыки: сигнатуры песен
Один из неприятных побочных эффектов БПФ заключается в том, что проведя анализ, мы теряем информацию о времени. (Хотя, теоретически, подобного можно избежать, но на практике для этого понадобится огромная вычислительная мощность.) Например, для трёхминутной песни мы можем видеть звуковые частоты и их амплитуды, но вот где именно в произведении эти частоты встречаются, не знаем. А это – важнейшая характеристика, которая делает музыкальное произведение тем, что оно есть! Нам нужно как-то узнать точные значения времени, когда появляется каждая из частот.
Именно поэтому мы будем пользоваться чем-то вроде скользящего окна, или блока данных, и подвергать трансформации лишь ту часть сигнала, которая в это «окно» попадает. Размер каждого блока можно определить с использованием различных подходов. Например, если мы записываем двухканальный звук с размером образца равным 16 бит и с частотой дискретизации 44100 Гц, одна секунда такого звука займёт 176 Кб памяти (44100 образцов * 2 байта * 2 канала). Если мы установим размер скользящего окна, равный 4 Кб, то каждую секунду нам нужно будет проанализировать 44 блока данных. Это – довольно высокое разрешение для детального анализа композиции.
Вернёмся к программированию.
byte audio [] = out.toByteArray()
int totalSize = audio.length
int sampledChunkSize = totalSize/chunkSize;
Complex[][] result = ComplexMatrix[sampledChunkSize][];
for(int j = 0;i < sampledChunkSize; j++) {
Complex[chunkSize] complexArray;
for(int i = 0; i < chunkSize; i++) {
complexArray[i] = Complex(audio[(j*chunkSize)+i], 0);
}
result[j] = FFT.fft(complexArray);
}Во внутреннем цикле мы помещаем данные из временной области (образцы звука) в комплексные числа с мнимой частью равной 0. Во внешнем цикле проходим по всем блокам данных и для каждого из них запускаем БПФ-анализ.
Как только у нас будут сведения о частотных характеристиках сигнала, можно приступать к формированию цифровой сигнатуры музыкального произведения. Это – самая важная часть всего процесса распознавания музыки, который реализует Shazam. Главная сложность здесь – выбрать из огромного количества частот именно те, которые важнее всего. Чисто интуитивно мы обращаем внимание на частоты с максимальными амплитудами (обычно их называют пиками).
Однако, в одной песне диапазон «сильных» частот может варьироваться, скажем, от ноты «до» контроктавы (32,70 Гц), до ноты «до» пятой октавы (4186,01 Гц). Это – огромный интервал. Поэтому, вместо того, чтобы за сразу проанализировать весь частотный диапазон, мы можем выбрать несколько более мелких интервалов. Выбор можно сделать, основываясь на частотах, которые обычно присущи важным музыкальным компонентам, и проанализировать их по отдельности. Например, можно воспользоваться интервалами, которые вот этот программист использовал для своей реализации алгоритма Shazam. А именно, это 30 Гц – 40 Гц, 40 Гц – 80 Гц и 80 Гц – 120 Гц для низких звуков (сюда попадает, например, бас-гитара). Для средних и более высоких звуков применяются частоты 120 Гц – 180 Гц и 180 Гц – 300 Гц (сюда входит вокал и большинство других инструментов).
Теперь, когда мы определились с интервалами, можно просто найти в них частоты с самыми высокими уровнями. Эти сведения и формируют сигнатуру для конкретного анализируемого блока данных, а она, в свою очередь, является частью сигнатуры всей песни.
public final int[] RANGE = new int[] { 40, 80, 120, 180, 300 };
// Функция для определения того, в каком диапазоне находится частота
public int getIndex(int freq) {
int i = 0;
while (RANGE[i] < freq)
i++;
return i;
}
// Результат – это комплексная матрица, полученная на предыдущем шаге
for (int t = 0; t < result.length; t++) {
for (int freq = 40; freq < 300 ; freq++) {
// Получим силу сигнала:
double mag = Math.log(results[t][freq].abs() + 1);
// Выясним, в каком мы диапазоне:
int index = getIndex(freq);
// Сохраним самое высокое значение силы сигнала и соответствующую частоту:
if (mag > highscores[t][index]) {
points[t][index] = freq;
}
}
// сформируем хэш-тег
long h = hash(points[t][0], points[t][1], points[t][2], points[t][3]);
}
private static final int FUZ_FACTOR = 2;
private long hash(long p1, long p2, long p3, long p4) {
return (p4 - (p4 % FUZ_FACTOR)) * 100000000 + (p3 - (p3 % FUZ_FACTOR))
* 100000 + (p2 - (p2 % FUZ_FACTOR)) * 100
+ (p1 - (p1 % FUZ_FACTOR));
}Заметьте, что мы должны учитывать то, что запись выполнена не в идеальных условиях (то есть, не в звукоизолированном помещении). Как результат, надо предусмотреть наличие в записи посторонних шумов и возможное искажение записываемого звука, зависящее от характеристик помещения. К этому вопросу стоит подойти очень серьёзно, в реальных системах стоит реализовать настройку анализа возможных искажений и посторонних звуков (fuzz factor) в зависимости от условий, в которых проводится запись.
Для упрощения поиска музыкальных композиций их сигнатуры используются как ключи в хэш-таблице. Ключам соответствуют значения времени, когда набор частот, для которых найдена сигнатура, появился в произведении, и идентификатор самого произведения (название песни и имя исполнителя, например). Вот вариант того, как подобные записи могут выглядеть в базе данных.
| Хэш-тег |
Время, в секундах |
Песня |
| 30 51 99 121 195 |
53.52 |
Песня A исполнителя A |
| 33 56 92 151 185 |
12.32 |
Песня B исполнителя B |
| 39 26 89 141 251 |
15.34 |
Песня C исполнителя C |
| 32 67 100 128 270 |
78.43 |
Песня D исполнителя D |
| 30 51 99 121 195 |
10.89 |
Песня E исполнителя E |
| 34 57 95 111 200 |
54.52 |
Песня A исполнителя A |
| 34 41 93 161 202 |
11.89 |
Песня E исполнителя E |
Если обработать таким способом некую библиотеку музыкальных записей, можно будет построить базу данных с полными сигнатурами каждого произведения.
Поиск совпадений
Для того чтобы выяснить, какая же песня играет сейчас в ресторане, надо записать звук с помощью телефона и прогнать его через вышеописанный процесс вычисления сигнатур. Затем можно запустить поиск вычисленных хэш-тегов в базе данных.
Но не всё так просто. Дело в том, что у многих фрагментов различных произведений хэш-тэги совпадают. Например, может оказаться так, что какой-то фрагмент песни A звучит точно так же, как некий участок песни E. И тут нет ничего удивительного. Музыканты и композиторы постоянно «заимствуют» друг у друга удачные музыкальные фигуры.
Всякий раз, когда удаётся обнаружить совпадающий хэш-тег, число возможных совпадений уменьшается, но весьма вероятно, что только лишь эти сведения не позволят нам настолько сузить диапазон поиска, чтобы остановиться на единственной правильной песне. Поэтому в алгоритме распознавания музыкальных произведений нам нужно проверять ещё кое-что. А именно – речь идёт об отметках времени.
Тот фрагмент песни, что записали в ресторане, может быть из любого её места, поэтому мы просто не в состоянии напрямую сравнивать относительное время внутри записанного фрагмента с тем, что есть в базе данных.
Однако если найдено несколько совпадений, можно проанализировать относительный тайминг совпадений, и, таким образом, повысить достоверность поиска.
Например, если взглянуть в вышеприведенную таблицу, можно обнаружить, что хэш-тег 30 51 99 121 195 относится и к песне A, и к песне E. Если секундой спустя мы будем проверять хэш-тег 34 57 95 111 200, то обнаружим ещё одно совпадение с песней A, к тому же, в подобном случаем мы будем знать о том, что совпадают и хэш-теги и их распределение во времени.
// Класс, который описывает конкретный момент в произведении
private class DataPoint {
private int time;
private int songId;
public DataPoint(int songId, int time) {
this.songId = songId;
this.time = time;
}
public int getTime() {
return time;
}
public int getSongId() {
return songId;
}
}Пусть i1 и i2 – это отметки времени в записанной песне, j1 и j2 – отметки времени в песне из базы данных. Мы можем говорить о том, что имеются два совпадения, с учётом совпадения разницы во времени, если выполняется следующее условие:
RecordedHash(i1) = SongInDBHash(j1) AND RecordedHash(i2) = SongInDBHash(j2)
AND
abs(i1 - i2) = abs (j1 - j2)Это даёт возможность не заботиться о том, на какую именно часть песни приходится запись: на начало, середину, или на самый конец.
И, наконец, маловероятно, что каждый обработанный фрагмент записанной в «диких» условиях песни совпадёт с аналогичным фрагментом из базы данных, построенной на основе студийных записей. Запись, на основе которой мы хотим найти название произведения, будет включать в себя много шума, что приведёт к неким расхождениям при сравнении. Поэтому, вместо того, чтобы пытаться исключить из списка совпадений всё, кроме единственной верной композиции, в конце процедуры сопоставления с базой данных мы отсортируем записи, в которых нашлись совпадения. Сортировать будем в убывающем порядке. Чем больше совпадений – тем вероятнее то, что мы нашли нужную композицию. Соответственно, она окажется на вершине списка.
Обзор процедуры распознавания музыки
Вот обзор всей процедуры распознавания музыкальных композиций. Пройдёмся по нему от начала до конца.
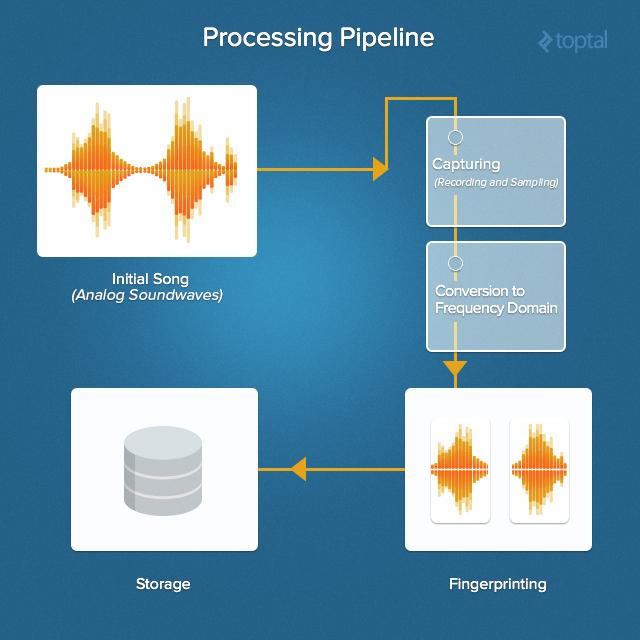
Обзор процедуры распознавания музыки
Всё начинается с исходного звука. Потом его захватывают, находят частотные характеристики, вычисляют хэш-теги и сравнивают их с теми, что хранятся в музыкальной базе данных.
В подобных системах базы данных могут быть просто огромными, поэтому важно использовать решения, которые поддаются масштабированию. В связях таблиц баз данных особенной нужды нет, модель данных очень проста, поэтому здесь вполне подойдёт какая-нибудь разновидность NoSQL-базы данных.
Shazam!
Программы, подобные той, о которой мы здесь говорили, подходят для поиска схожих мест в музыкальных произведениях. Теперь, когда вы понимаете, как работает Shazam, вы можете увидеть, что алгоритмы распознавания музыки применимы не только в роли «напоминалок» названий забытых песен из прошлого, звучащих по радио в такси.
Например, с их помощью можно искать музыкальный плагиат, или задействовать их для того, чтобы найти исполнителей, которые вдохновляли некоторых первопроходцев в блюзе, джазе, в рок-музыке, в поп-музыке, да в любом другом жанре.
Возможно, хорошим экспериментом станет заполнение базы данных классикой – сочинениями Баха, Бетховена, Вивальди, Вагнера, Шопена и Моцарта и поиск схожего в их работах. Так вполне можно выяснить, что даже Боб Дилан, Элвис Пресли и Роберт Джонсон не прочь были что-нибудь позаимствовать у других!
Но можем ли мы их за это винить? Уверен, что нет. Ведь музыка – это всего лишь звуковая волна, которую человек слышит, запоминает и повторяет у себя в голове. Там она развивается, меняется – до тех пор, пока её не запишут в студии и не выпустят на волю, где она вполне может вдохновить очередного гения от музыки.
О, а приходите к нам работать? :)wunderfund.io — молодой фонд, который занимается высокочастотной алготорговлей. Высокочастотная торговля — это непрерывное соревнование лучших программистов и математиков всего мира. Присоединившись к нам, вы станете частью этой увлекательной схватки.
Мы предлагаем интересные и сложные задачи по анализу данных и low latency разработке для увлеченных исследователей и программистов.
Гибкий график и никакой бюрократии, решения быстро принимаются и воплощаются в жизнь.
Присоединяйтесь к нашей команде: wunderfund.io