В этом году исследователи из Google Brain опубликовали статью под названием Exploring the Limits of Language Modeling (Исследование границ языкового моделирования), в которой была описана языковая модель, позволившая значительно снизить перплексию (с примерно 50 до 30) на словаре One Billion Word Benchmark.
В этом посте мы расскажем про самый низкий уровень этой модели — представление символов.
Для начала определим само понятие языковой модели. Языковая модель — это вероятностное распределение на множестве словарных последовательностей. Для предложения вроде “Hello world” или “Buffalo buffalo Buffalo buffalo buffalo buffalo Buffalo buffalo” языковая модель выдаст нам вероятность того, что мы встретим это предложение.
Оценкой качества языковой модели служит перплексия (perplexity) — мера того, насколько хорошо модель предсказывает детали тестовой коллекции (чем меньше перплексия, тем лучше модель).
Языковая модель
("<S>" и "</S>" обозначают начало и конец предложения).
Это сокращенное название сверточной нейронной сети уровня символов (character-level convolutional neural network). Если вы не знаете, что это, — забудьте то, что я сейчас сказал, так как в этом посте мы сосредоточится на том, что происходит то того, как сеть начнет выполнять какие-либо свертки, а именно, на character embedding.
Самый очевидный способ представления символа как входного значения для нашей нейронной сети — это прямое кодирование (one-hot encoding). Например, алфавит, состоящий из латинских букв нижнего регистра, мы представили бы так:
И так далее. Вместо этого мы научимся “плотному” (dense) представлению каждого символа. Если вы уже использовали системы векторного представления слов, подобные word2vec, то этот способ покажется вам знакомым.
Первый слой Char CNN отвечает за перевод необработанных символов входного слова в векторное представление, которое передается на вход сверточным фильтрам.
В
Это довольно сложно осмыслить. Давайте снизим размерность представления символов до двух с помощью алгоритма t-SNE, чтобы представить, где они будут располагаться относительно друг друга. t-SNE так расположит наше представление, что пары с наименьшим расстоянием в 16-мерном векторном пространстве будут также располагаться ближе друг другу в двумерной проекции.

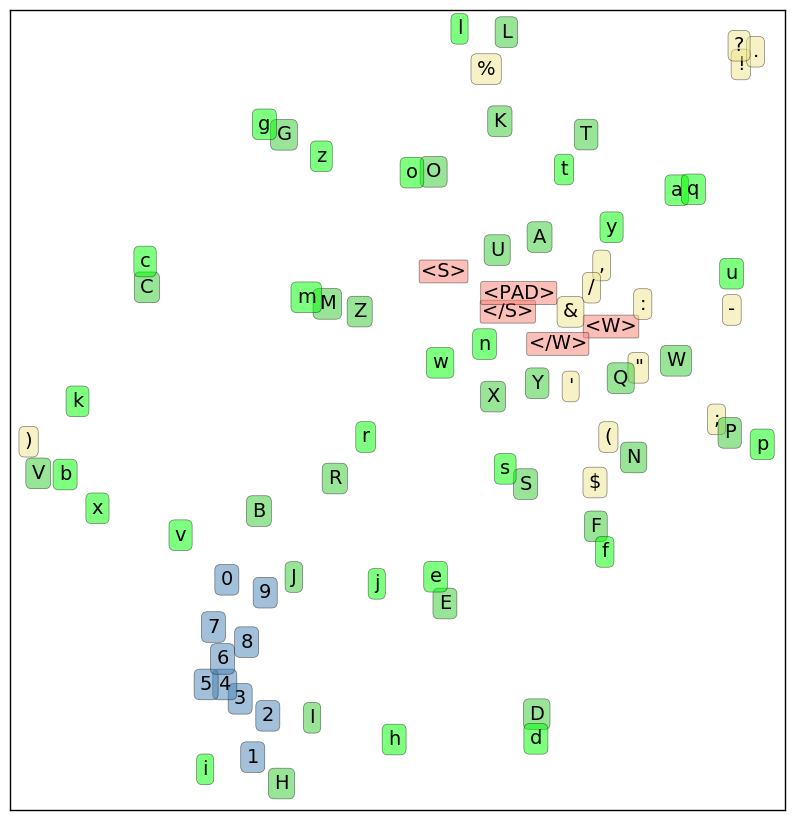
t-SNE представление наиболее частотных символов. Розовые отметки соответствуют специальным мета-символам. <S> и </S> отмечают начало и конец предложения. <W> и </W> отмечают начало и конец слова. <PAD> используется ограничения длины слов 50-ю символами. Желтые отметки — знаки пунктуации, синие — цифры, а светло- и темно-зеленые — буквенные символы верхнего и нижнего регистров.
Здесь бросаются в глаза несколько интересных закономерностей:
Также стоит отметить отсутствие закономерности. Кроме не слишком регулярного соответствия пар строчных/заглавных, в остальном расположение букв кажется случайным. Они достаточно удалены друг от друга и размазаны по всей плоскости проекции. Не наблюдается, к примеру, островков гласных или сонорных согласных. Нет и универсального отделения строчных букв от заглавных.
Возможно, эта информация и отражается в представлении, но у t-SNE просто нет достаточного количества степеней свобод, чтобы отразить эти отличия в двумерной проекции. Может быть, исследовав каждую измерение по очереди, мы могли бы получить больше информации?
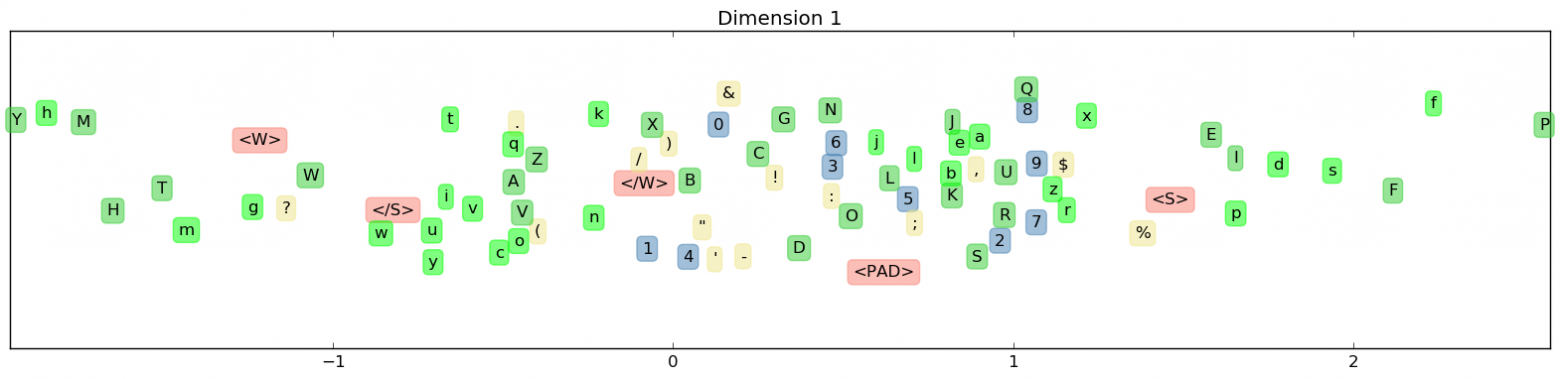
А может быть и нет. Можете взглянуть на графики всех 16-ти измерений здесь — у меня не получилось найти в них какие-либо закономерности.
Возможно, самая известная особенности векторных представлений слов — возможность складывать и вычитать их и (иногда) получать семантически значимые результаты. Например,
Интересно, можем ли мы проделывать то же самое с представлением символов. Здесь не слишком много очевидных аналогий, но как насчет того, чтобы складывать и вычитать “заглавность”?
‘a’ относится к ‘A’ так же, как ‘b’ относится к…
Ладно, не слишком удачное начало. Попробуем еще:
Частичный успех?
Сделав множество попыток, мы то и дело получали верный ответ, но чем этот способ лучше случайного? Не забывайте, что половина строчных букв располагаются в близком соседстве с соответствующими заглавными. Уже поэтому, если мы будем двигаться от буквы в случайном направлении, мы со значительной долей вероятности наткнемся на ее пару.
Думаю, остается попробовать только одно:
Заметка на будущее: никогда не использовать character embedding для расчета чаевых.
Кажется полезным размещать близкие по величине цифры близко друг к другу по причине взаимозаменяемости. “36-летний” можно легко заменить на “37-летний” (или даже “26-летний”), 800 баксов больше похожи на 900 или 700 баксов, чем на 100. Глядя на нашу t-SNE проекцию, можем сказать, что такая модель работает. Но это не означает, что цифры выстроены в линию (начнем хотя бы с того, что модели необходимо выучит некоторые тонкости, связанные с цифрами, например, учесть, что год чаще всего начинается с “19” или “20”).
Прежде чем угадывать, почему определенный символ представлен так, а не иначе, стоит спросить: зачем вообще используют character embedding?
Одной из причин может быть уменьшение сложности модели. Фильтрам выделения признаков в Char CNN для каждого символа будет достаточно запомнить 16 весов вместо 256. Если мы уберем слой векторного представления, количество весов на этапе выделения признаков увеличится в 16 раз, то есть примерно с 460К (4096 фильтров * максимальная ширина 7 * 16-мерное представление) до 7.3М. Кажется, что это много, но ведь общее количество параметров для всей сети (CNN + LSTM + Softmax) составляет 1.04 миллиарда! Так что парочка лишних миллионов не сыграет большой роли.
На самом деле
По-видимому, под лучшей производительностью имелась в виду более низкая перплексия, а не скорость обучения модели, например.
Почему же представление символов улучшает производительность? Хорошо, а почему представление слов улучшает производительность задач области естественных языков? Они улучшают генерализацию. В языке множество слов, и многие из них встречаются редко. Если вы встречаем слова “малина”, “клубника” и “крыжовник” в одинаковом контексте, мы присваиваем им близкие векторы. И если нам не раз встречались словосочетания “варенье из малины” и “варенье из клубники”, можем предположить, что и сочетание “варенье из крыжовника” достаточно вероятно, даже если мы ни разу не встретили его в нашем корпусе.
Начнем с того, что аналогия с векторами слов здесь не вполне уместна. Корпус Billion Word состоит из 800 000 отдельных слов, в то время как мы имеет дело всего с 256 символами. Стоит ли думать о генерализации? И как обобщить, например, ‘g’ на другой символ?
Кажется, ответ будет “никак”. Иногда мы можем делать выводы на основе генерализации для заглавных и строчных версий одной буквы, но в целов буквенные символы обособлены, и все они встречаются так часто, что нас не должна заботить генерализация.
Но нет ли символов, которые встречаются достаточно редко, чтобы генерализация могла сыграть важную роль? Давайте посмотрим.
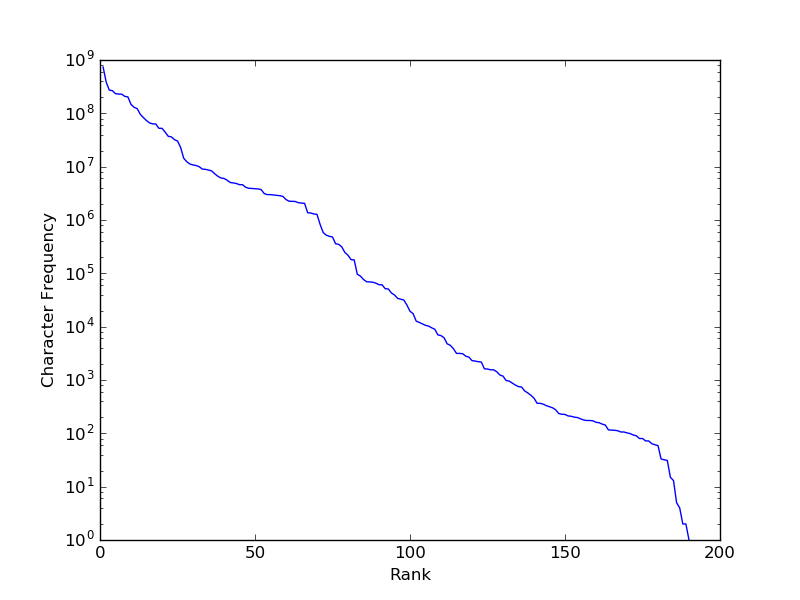
Частота появления n-го наиболее популярного символа. Рассчитано на основе обучающего множества Billion Word Benchmark (около 770 тысяч слов). 50 с лишним символов полностью отсутствуют в корпусе (например, управляющие символы ASCII).
Да, это не совсем закон Ципфа (мы приближаемся к прямой линии, используя только логарифмическую шкалу по оси y вместо двойной логарифмической), но все же видно, что существует большое количество редко используемых символов (в основном это не-ASCII символы и редкие знаки пунктуации).
Возможно, наше векторное представление помогает нам использовать генерализацию для выводов о таких символах. На графике t-SNE выше я изобразил только те символы, которые встречаются достаточно часто (за нижнюю границу я взял наименее частотный буквенный символ ‘x’). Что если мы изобразим представление для символов, встречающихся в корпусе хотя бы 50 раз?
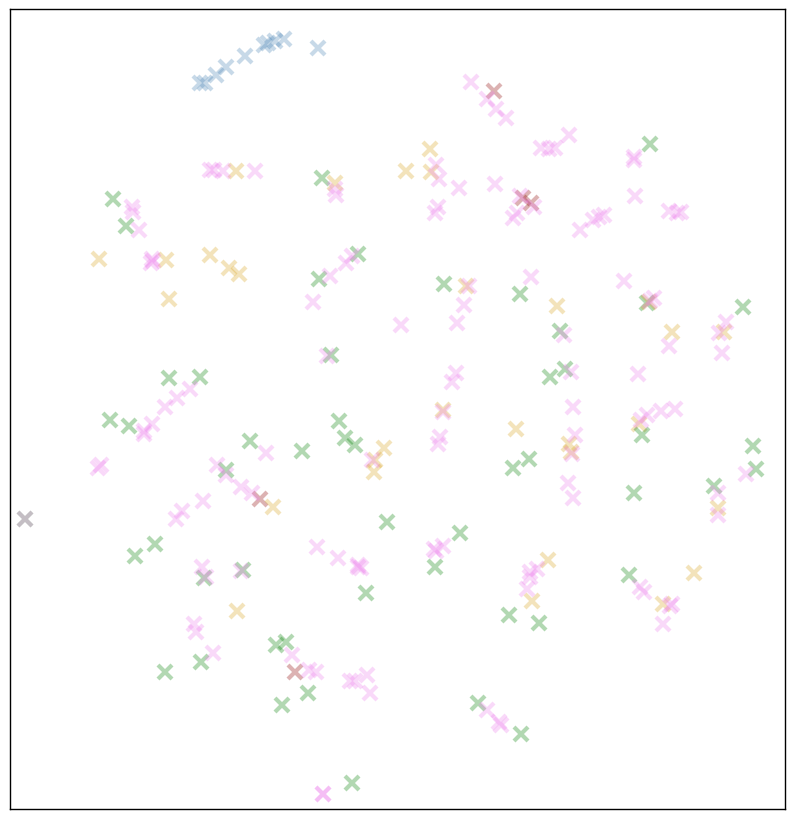
Зеленые=буквы, синие=цифры, желтые=знаки препинания, красно-коричневые=метасимволы. Розовые отметки — байты до 127 и все остальное, что не вошло в предыдущие группы.
Кажется, это подтверждает нашу гипотезу! Буквы, как и прежде, антисоциальны и редко касаются друг друга. Но на нескольких участках наши редкие “розовые” символы формируют плотные кластеры или линии.
Наиболее вероятное предположение: буквенные символы стоят отдельно, в то время как редкие символы, а также символы с высокой степенью взаимозаменяемости (цифры, знаки препинания на конце предложения) имеют свойство располагаться близко друг к другу.
На этом пока все. Спасибо команде Google Brain за выпуск
В следующий раз мы рассмотрим второй этап Char CNN — сверточные фильтры.
В этом посте мы расскажем про самый низкий уровень этой модели — представление символов.

Введение: языковые модели
Для начала определим само понятие языковой модели. Языковая модель — это вероятностное распределение на множестве словарных последовательностей. Для предложения вроде “Hello world” или “Buffalo buffalo Buffalo buffalo buffalo buffalo Buffalo buffalo” языковая модель выдаст нам вероятность того, что мы встретим это предложение.
Оценкой качества языковой модели служит перплексия (perplexity) — мера того, насколько хорошо модель предсказывает детали тестовой коллекции (чем меньше перплексия, тем лучше модель).
Языковая модель
lm_1b берет одно слово из предложения и вычисляет вероятностное распределение следующего слова. Таким образом, она может вычислить вероятность такого предложения, как “Hello, world”, следующим образом:P("<S> Hello world . </S>") = product(P("<S>"), P("Hello" | "<S>"),
P("world" | "<S> Hello"), P("." | "<S> Hello world"),
P("</S>" | "<S> Hello world ."))("<S>" и "</S>" обозначают начало и конец предложения).
Архитектура lm_1b
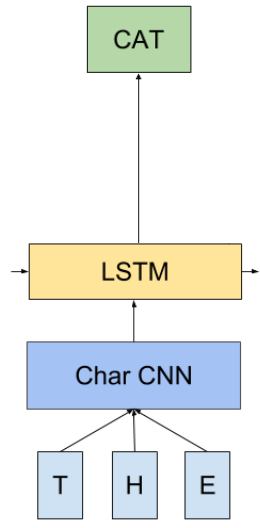
lm_1b состоит из трех основным компонентов (см. рисунок):
- Char CNN (синий прямоугольник) получает на вход символы, из которых состоит слово, выводит векторное представление слова (word embedding).
- LSTM (Long short-term memory) (желтый) получает представление слова, а также вектор состояния (state vector) (например, слова, которые уже встречались в данном предложении) и вычисляет представление следующего слова.
- Последний слой, softmax (зеленый), с учетом информации, полученной от LSTM, вычисляет распределение относительно всех слов словаря.
Char CNN
Это сокращенное название сверточной нейронной сети уровня символов (character-level convolutional neural network). Если вы не знаете, что это, — забудьте то, что я сейчас сказал, так как в этом посте мы сосредоточится на том, что происходит то того, как сеть начнет выполнять какие-либо свертки, а именно, на character embedding.
Character Embedding
Самый очевидный способ представления символа как входного значения для нашей нейронной сети — это прямое кодирование (one-hot encoding). Например, алфавит, состоящий из латинских букв нижнего регистра, мы представили бы так:
onehot('a') = [1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]
onehot('c') = [0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]И так далее. Вместо этого мы научимся “плотному” (dense) представлению каждого символа. Если вы уже использовали системы векторного представления слов, подобные word2vec, то этот способ покажется вам знакомым.
Первый слой Char CNN отвечает за перевод необработанных символов входного слова в векторное представление, которое передается на вход сверточным фильтрам.
В
lm_1b алфавит имеет размерность 256 (не-ASCII символы расширены до нескольких байт, каждый из которых кодируется отдельно) и отображается на пространство размерности 16. Например, символ ‘a’ представлен следующим вектором:array([ 1.10141766, -0.67602301, 0.69620615, 1.96468627, 0.84881932,
0.88931531, -1.02173674, 0.72357982, -0.56537604, 0.09024946,
-1.30529296, -0.76146501, -0.30620322, 0.54770935, -0.74167275,
1.02123129], dtype=float32)Это довольно сложно осмыслить. Давайте снизим размерность представления символов до двух с помощью алгоритма t-SNE, чтобы представить, где они будут располагаться относительно друг друга. t-SNE так расположит наше представление, что пары с наименьшим расстоянием в 16-мерном векторном пространстве будут также располагаться ближе друг другу в двумерной проекции.

t-SNE представление наиболее частотных символов. Розовые отметки соответствуют специальным мета-символам. <S> и </S> отмечают начало и конец предложения. <W> и </W> отмечают начало и конец слова. <PAD> используется ограничения длины слов 50-ю символами. Желтые отметки — знаки пунктуации, синие — цифры, а светло- и темно-зеленые — буквенные символы верхнего и нижнего регистров.
Здесь бросаются в глаза несколько интересных закономерностей:
- Цифры не только сгруппированы вместе, кроме этого они расположены по порядку и “змейкой”.
- В большинстве случаев одни и те же буква в верхнем и нижнем регистре расположены рядом, но некоторые (например, k/K) значительно удалены друг от друга.
- В правом верхнем углу скучились знаки пунктуации, которые могут завершать предложение (
.?!). - Метасимволы (розовые) образуют так называемый рыхлый кластер, а остальные специальные символы — еще более рыхлый (с ‘%’ и ‘)’ в качестве выпадающих значений).
Также стоит отметить отсутствие закономерности. Кроме не слишком регулярного соответствия пар строчных/заглавных, в остальном расположение букв кажется случайным. Они достаточно удалены друг от друга и размазаны по всей плоскости проекции. Не наблюдается, к примеру, островков гласных или сонорных согласных. Нет и универсального отделения строчных букв от заглавных.
Возможно, эта информация и отражается в представлении, но у t-SNE просто нет достаточного количества степеней свобод, чтобы отразить эти отличия в двумерной проекции. Может быть, исследовав каждую измерение по очереди, мы могли бы получить больше информации?

А может быть и нет. Можете взглянуть на графики всех 16-ти измерений здесь — у меня не получилось найти в них какие-либо закономерности.
Векторные вычисления
Возможно, самая известная особенности векторных представлений слов — возможность складывать и вычитать их и (иногда) получать семантически значимые результаты. Например,
vec('woman') + (vec('king') - vec('man')) ~= vec('queen')Интересно, можем ли мы проделывать то же самое с представлением символов. Здесь не слишком много очевидных аналогий, но как насчет того, чтобы складывать и вычитать “заглавность”?
def analogy(a, b, c):
"""a is to b, as c is to ___,
Return the three nearest neighbors of c + (b-a) and their distances.
"""
# ...‘a’ относится к ‘A’ так же, как ‘b’ относится к…
>>> analogy('a', 'A', 'b')
b: 4.2
V: 4.2
Y: 5.1Ладно, не слишком удачное начало. Попробуем еще:
>>> analogy('b', 'B', 'c')
c: 4.2
C: 5.2
+: 5.9
>>> analogy('b', 'B', 'd')
D: 4.2
,: 4.9
d: 5.0
>>> analogy('b', 'B', 'e')
N: 4.7
,: 4.7
e: 5.0Частичный успех?
Сделав множество попыток, мы то и дело получали верный ответ, но чем этот способ лучше случайного? Не забывайте, что половина строчных букв располагаются в близком соседстве с соответствующими заглавными. Уже поэтому, если мы будем двигаться от буквы в случайном направлении, мы со значительной долей вероятности наткнемся на ее пару.
Векторные вычисления (теперь по-настоящему)
Думаю, остается попробовать только одно:
>>> analogy('1', '2', '2')
2: 2.4
E: 3.6
3: 3.6
>>> analogy('3', '4', '8')
8: 1.8
7: 2.2
6: 2.3
>>> analogy('2', '5', '5')
5: 2.7
6: 4.0
7: 4.0
# It'd be really surprising if this worked...
>>> nearest_neighbors(vec('2') + vec('2') + vec('2'))
2: 6.0
1: 6.9
3: 7.1Заметка на будущее: никогда не использовать character embedding для расчета чаевых.
Кажется полезным размещать близкие по величине цифры близко друг к другу по причине взаимозаменяемости. “36-летний” можно легко заменить на “37-летний” (или даже “26-летний”), 800 баксов больше похожи на 900 или 700 баксов, чем на 100. Глядя на нашу t-SNE проекцию, можем сказать, что такая модель работает. Но это не означает, что цифры выстроены в линию (начнем хотя бы с того, что модели необходимо выучит некоторые тонкости, связанные с цифрами, например, учесть, что год чаще всего начинается с “19” или “20”).
К чему все это?
Прежде чем угадывать, почему определенный символ представлен так, а не иначе, стоит спросить: зачем вообще используют character embedding?
Одной из причин может быть уменьшение сложности модели. Фильтрам выделения признаков в Char CNN для каждого символа будет достаточно запомнить 16 весов вместо 256. Если мы уберем слой векторного представления, количество весов на этапе выделения признаков увеличится в 16 раз, то есть примерно с 460К (4096 фильтров * максимальная ширина 7 * 16-мерное представление) до 7.3М. Кажется, что это много, но ведь общее количество параметров для всей сети (CNN + LSTM + Softmax) составляет 1.04 миллиарда! Так что парочка лишних миллионов не сыграет большой роли.
На самом деле
lm_1b включает в себя char embedding, потому что их Char CNN разработана на основе статьи авторства Kim et. al 2015 года, где также использовался char embedding. Сноска в этой статье объясняет:Так как |C| обычно мало, некоторые авторы применяют прямое кодирование для векторного представления символов. Тем не менее, мы обнаружили, что использование представления символов меньших размерностей показываем немного лучшую производительность.
По-видимому, под лучшей производительностью имелась в виду более низкая перплексия, а не скорость обучения модели, например.
Почему же представление символов улучшает производительность? Хорошо, а почему представление слов улучшает производительность задач области естественных языков? Они улучшают генерализацию. В языке множество слов, и многие из них встречаются редко. Если вы встречаем слова “малина”, “клубника” и “крыжовник” в одинаковом контексте, мы присваиваем им близкие векторы. И если нам не раз встречались словосочетания “варенье из малины” и “варенье из клубники”, можем предположить, что и сочетание “варенье из крыжовника” достаточно вероятно, даже если мы ни разу не встретили его в нашем корпусе.
Генерализация символов?
Начнем с того, что аналогия с векторами слов здесь не вполне уместна. Корпус Billion Word состоит из 800 000 отдельных слов, в то время как мы имеет дело всего с 256 символами. Стоит ли думать о генерализации? И как обобщить, например, ‘g’ на другой символ?
Кажется, ответ будет “никак”. Иногда мы можем делать выводы на основе генерализации для заглавных и строчных версий одной буквы, но в целов буквенные символы обособлены, и все они встречаются так часто, что нас не должна заботить генерализация.
Но нет ли символов, которые встречаются достаточно редко, чтобы генерализация могла сыграть важную роль? Давайте посмотрим.

Частота появления n-го наиболее популярного символа. Рассчитано на основе обучающего множества Billion Word Benchmark (около 770 тысяч слов). 50 с лишним символов полностью отсутствуют в корпусе (например, управляющие символы ASCII).
Да, это не совсем закон Ципфа (мы приближаемся к прямой линии, используя только логарифмическую шкалу по оси y вместо двойной логарифмической), но все же видно, что существует большое количество редко используемых символов (в основном это не-ASCII символы и редкие знаки пунктуации).
Возможно, наше векторное представление помогает нам использовать генерализацию для выводов о таких символах. На графике t-SNE выше я изобразил только те символы, которые встречаются достаточно часто (за нижнюю границу я взял наименее частотный буквенный символ ‘x’). Что если мы изобразим представление для символов, встречающихся в корпусе хотя бы 50 раз?
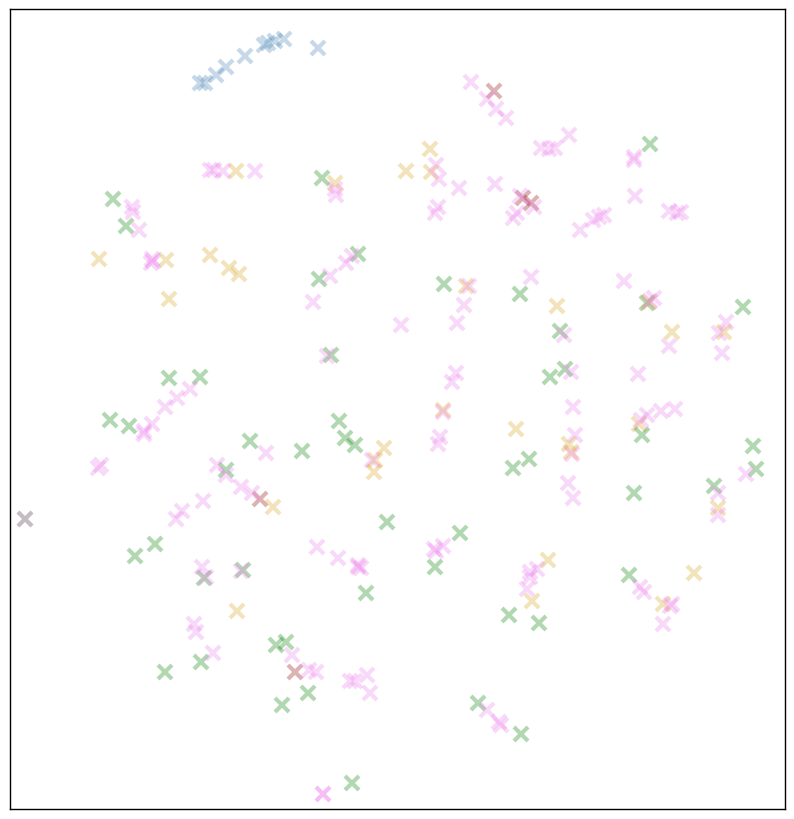
Зеленые=буквы, синие=цифры, желтые=знаки препинания, красно-коричневые=метасимволы. Розовые отметки — байты до 127 и все остальное, что не вошло в предыдущие группы.
Кажется, это подтверждает нашу гипотезу! Буквы, как и прежде, антисоциальны и редко касаются друг друга. Но на нескольких участках наши редкие “розовые” символы формируют плотные кластеры или линии.
Наиболее вероятное предположение: буквенные символы стоят отдельно, в то время как редкие символы, а также символы с высокой степенью взаимозаменяемости (цифры, знаки препинания на конце предложения) имеют свойство располагаться близко друг к другу.
На этом пока все. Спасибо команде Google Brain за выпуск
lm_1b. Если хотите провести свои эксперименты с этой моделью, не забудьте ознакомиться и инструкциями здесь. Я выложил скрипты, с помощью которых делал визуализации для этого поста сюда — не стесняйтесь переиспользовать или изменять их, хотя выглядят они ужасно.В следующий раз мы рассмотрим второй этап Char CNN — сверточные фильтры.
О, а приходите к нам работать? :)wunderfund.io — молодой фонд, который занимается высокочастотной алготорговлей. Высокочастотная торговля — это непрерывное соревнование лучших программистов и математиков всего мира. Присоединившись к нам, вы станете частью этой увлекательной схватки.
Мы предлагаем интересные и сложные задачи по анализу данных и low latency разработке для увлеченных исследователей и программистов. Гибкий график и никакой бюрократии, решения быстро принимаются и воплощаются в жизнь.
Присоединяйтесь к нашей команде: wunderfund.io