16 апреля открылся новый набор в Школу анализа данных Яндекса, который продлится до 15 мая. В этом посте я хочу рассказать вам, как сложилась судьба тех, кто уже закончил ШАД, а также впервые публично разберу все задания нашего письменного вступительного экзамена. Как всегда, желающим надо будет заполнить анкету и выполнить задание на сайте Школы, сдать письменный экзамен и пройти собеседование.
Кстати, если у вас есть знакомые или их дети, которым рано идти в ШАД, но которые подают надежды, расскажите им о факультете Computer Science, который открывается в этом году в Высшей школе экономики при участии Яндекса. Во многом он будет расти из Школы анализа данных, но в неё мы принимаем студентов и выпускников. Поэтому если вы абитуриент, то приходите 27 апреля на презентацию этого факультета, где ректор НИУ ВШЭ Ярослав Кузьминов и сооснователь Яндекса Аркадий Волож расскажут о нём все подробности. Мы всех приглашаем.
С момента создания ШАД её закончили 260 специалистов в области computer science. Мы попросили двух выпускников Школы рассказать о том, что им дало обучение в ней, и дать несколько советов тем, кто решил поступать.
Андрей Петров, разработчик в мюнхенском офисе Google.
Алексей Умнов, выпускник ШАД. Разработчик в группе морфологии Поиска в Яндексе, аспирант ВМК МГУ.
Разбор вступительных задач
На этот раз мы решили впервые публично разобрать все задания письменного вступительного экзамена в Школу анализа данных. К нему допускаются только те, кто успешно справился с заданием в анкете. В прошлом году из 617 человек приглашение на него получили 284, а успешно сдали и дошли до собеседования — 132.
Последовательность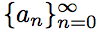 определена рекурсивно.
определена рекурсивно.
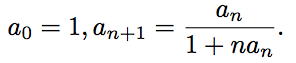
Найдите формулу общего члена последовательности.
Решение
Введем обозначение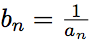 Тогда
Тогда 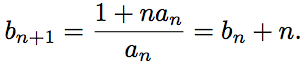
Кроме того,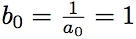 . Получаем, что
. Получаем, что 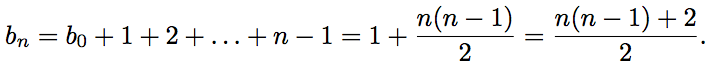
Отсюда получаем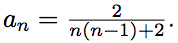
Даём множество A = {1,2,...,n}. Среди всех его подмножеств равновероятно выбираем k его подмножеств A1,…,Ak. Найдите вероятность того, чтоA1 ∩ A2 ∩ … ∩ Ak = ∅ .
Решение
Рассмотрим элемент i ∈ A. Очевидно, подмножеств в A, содержащих i и не содержащих i, равное количество. Таким образом вероятность того, что i лежит в Aj равна 1/2. Эти вероятности независимы для разных j. Получаем, что вероятность того, что i содержится вA1 ∩ A2 ∩ … ∩ Ak равна 1/2k. Соответственно, вероятность того, что i не содержится в A1 ∩ A2 ∩ … ∩ Ak , равна 1 — 1/2k . Эти вероятности независимы в разных i. Получается, что вероятность того, что ни один из номеров i не попал в A1 ∩ A2 ∩ … ∩ Ak равна (1 — 1/2k)n .
Дан массив длины n из нулей и единиц. Найдите в нём подмассив макисмальной длины, в котором количество единиц равно количеству нулей. Ограничения: O(n) по времени и O(n) по дополнительной памяти.
Решение
Обозначим исходный массив через a[・]. Заведём еще четыре массива длины n: b[・], c[・], d[・] и e[・]. Пройдём по возрастанию индексов и заполним массив b[・] по правилу:b[0] = 2 ・ a[0] — 1, b[i] =b[i — 1] + 2a[i] — 1 при i > 0. Иными словами, если в массиве a[・] заменить нули на -1, то в массиве b[・] будут стоять суммы от a[0] до a[i]. Заполним массивы c[・] и d[・] минус единицами. Далее идём по возрастанию номеров по массиву b[・]. Если b[i] = k, то d[k] = i, если при этом выполнено c[k] = -1, то присваиваем c[k] = i.
Далее, когда мы прошли по всему массиву b[・], заполним массив e[・] по правилу e[i] = d[i] — c[i]. Заметим, что если в массиве a[・] есть подмассив от a[m] до a[l], в котором равное количество единиц и нулей, то b[m] = b[l] = k. И тогда c[k] — это минимальный номер i такой, что b[i] = k, а d[k] — максимальный. Соответственно, e[k] — максимальное расстояние между m и l, где b[m] = b[l] = k. Найдём максимум массива e[・]. (Очевидно, это можно сделать за O(n) операций.) пусть он равен e[j]. Тогда искомы подмассив — это подмассив от a[c[j]] до a[d[j]]
Пусть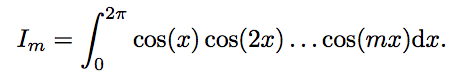
Для каких m ∈ [0, 10] Im≠0?
Решение
Многократно воспользуемся формулой:
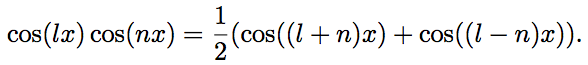
С помощью этой формулы получим:
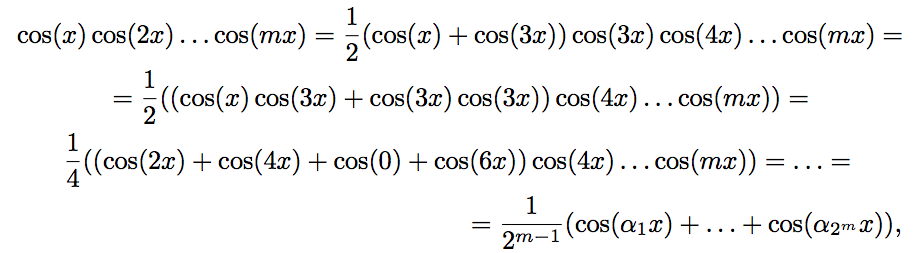 где ai = 1 ± 2 ± 3 … ± m ∈ Z. Несложно убедиться, что чётности всех чисел ai будут одинаковы. Более того, в случаях m = 4k и m = 4k + 3 все ai чётны. Если ai ≠ 0, то
где ai = 1 ± 2 ± 3 … ± m ∈ Z. Несложно убедиться, что чётности всех чисел ai будут одинаковы. Более того, в случаях m = 4k и m = 4k + 3 все ai чётны. Если ai ≠ 0, то 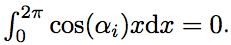
Значит, при m = 4k + 1 и m = 4k + 2, Im = 0. Если же m = 4k или 4k + 3, то среди ai обязательно есть ноль, так как между числами 1, 2, …, m можно так расствить знаки «+» и «—», чтобы получился ноль. Действительно,
(1 − 2 − 3 + 4) + (5 − 6 − 7 + 8) +... + ((4k − 3) − (4k − 2) − (4k − 1) + 4k = 0,
(1 + 2 − 3) + (4 − 5 − 6 + 7) +... + (4k − (4k + 1) − (4k + 2) + (4k + 3)) = 0.
Таким образом, m = 4k и 4k + 3, Im = 0. Ответ: при m = 0,3,4,7,8.
Дан неориентированный граф G без петель. Пронумеруем все его вершины. Матрица смежности графа G с конечным числом вершин n (пронумерованных числами от 1 до n) — это квадратная матрица A размера n, в которой значение элемента aij равно числу рёбер из i-ой вершины графа в j-ю вершину.
Докажите, что матрица A имеет отрицательное собственное значение.
Решение
Утверждение задачи не свосем верно. Если в графе нет рёбер, то матрица нулевая и все собственные значения равны нулю. Если же рёбра есть, то A — симметрическая матрица с неотрицательными элементами и нулями на диагонали. Докажем, что у такой матрицы есть неотрицательное собственное значение.
Известный факт, что симметрическая матрица диагонализуема в вещественном базисе. (Все собственные значения вещественны.) Допустим, что все собственные значения A неотрицательны. Рассмотрим квадратичную форму q с матрицей A в базисе {e1, … ,en}. Тогда эта квадратичная форма неотрицательно определена, так как все собственные значения неотрицательны. То есть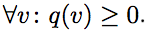 С другой стороны, пусть aij≠ 0. Тогда
С другой стороны, пусть aij≠ 0. Тогда q(ei — ej) = aii — 2aij + ajj= -2aij < 0. Это противоречит неотрицательно определённости q. Значит исходное предположение неверно, и у A есть отрицательное собственное значение.
Рассмотрим бесконечный двумерный массив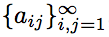 , состоящий из натуральных чисел, причём каждое число встречается ровно 8 раз. Докажите, что
, состоящий из натуральных чисел, причём каждое число встречается ровно 8 раз. Докажите, что ∃ (m,n): amn > mn .
Решение
Допустим, что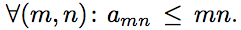 . Выберем некоторое k ∈ N и рассмотрим кривую на плоскости y = k/x. Если i,j ∈ N и точка (i,j) лежит под кривой y=k/x, то aij ≤ ij ≤ i・k/i= k. Таким образом, количество целых точек под кривой y = k/x должно быть не больше 8k. С другой стороны, количество целых точек под этой кривой не меньше, чем
. Выберем некоторое k ∈ N и рассмотрим кривую на плоскости y = k/x. Если i,j ∈ N и точка (i,j) лежит под кривой y=k/x, то aij ≤ ij ≤ i・k/i= k. Таким образом, количество целых точек под кривой y = k/x должно быть не больше 8k. С другой стороны, количество целых точек под этой кривой не меньше, чем 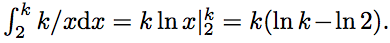 При достаточно большом k это число больше 8k. Таким образом, мы получаем противоречие. Следовательно, найдётся пара (m,n) такая, что : amn>mn.
При достаточно большом k это число больше 8k. Таким образом, мы получаем противоречие. Следовательно, найдётся пара (m,n) такая, что : amn>mn.
Дана матрица из нулей и единиц, причём для каждой строки матрицы верно следующее: если в строке есть единицы, то они все идут подряд (неразрывной группой из единиц). Докажите, что определитель такой матрицы может быть равен ±1 или 0.
Решение
Переставляя строки, мы можем добиться того, чтобы позиции первых (слева) единиц не убывали сверху вниз. При этом определитель либо не изменится, либо поменяет знак. Если у двух строк позиции первых единиц совпадают, то вычтем ту, в которой меньше единиц из той, в которой больше. Определитель при этом не меняется. Такими операциями мы можем добиться того, что позиции первых единиц строго возрастают сверху вниз. При этом либо матрица окажется вырожденной, либо верхнетреугольной с единицами на диагонали. То есть, определитель станет либо 0, либо 1. Так как определитель при наших операциях либо не менялся, либо поменял знак, изначальный определитель был ±1 или 0.
В ШАД преподают известные российские учёные. Например, курс по анализу данных разработал и ведёт Илья Мучник, профессор Rutgers University. Когда-то он был научным руководителем Аркадия Воложа. Теорию машинного обучения, без которого невозможно представить работу с большими объемами данных, преподаёт Алексей Червоненкис, профессор Лондонского университета и один из создателей отечественной школы анализа данных. Программу отделения Computer Science разрабатывал в том числе и Илья Сегалович. Мы создавали ШАД, чтобы вырастить поколение программистов, которые могут применять академические знания в прикладных задачах. Поэтому у нас преподают не только учёные, но и сотрудники Яндекса.
В прошлом году мы получили 617 заявок на поступление, 284 человека были приглашены на письменный экзамен. Но это не последнее испытание для поступающих в Школу. По результатам экзамена мы приглашаем на собеседования. Из 132 человек, которые его успешно сдали и дошли до собеседований, на первый курс было зачислено 97 человек.
Как многие из вас могут помнить, ШАД появилась в 2007 году. Сейчас у нас есть филиалы в Екатеринбурге, Киеве, Минске и Новосибирске. В Санкт-Петербурге отделение ШАД открыто при Computer Science Center.
Обучение на курсах длится два года. Программа разделена на три типа курсов: теоретические («Дискретный анализ», «Комбинаторика», «Вероятность», «Теория сложности»), практические («Обучение программированию на С++», «Java», «Параллельные и распределенные вычисления») и смешанные («Алгоритмы и структуры данных», «Машинное обучение», «Компьютерная лингвистика» и т.д.). Учиться можно и на заочном отделении, общаясь с преподавателями по электронной почте и пользуясь видеолекциями.
Кстати, если у вас есть знакомые или их дети, которым рано идти в ШАД, но которые подают надежды, расскажите им о факультете Computer Science, который открывается в этом году в Высшей школе экономики при участии Яндекса. Во многом он будет расти из Школы анализа данных, но в неё мы принимаем студентов и выпускников. Поэтому если вы абитуриент, то приходите 27 апреля на презентацию этого факультета, где ректор НИУ ВШЭ Ярослав Кузьминов и сооснователь Яндекса Аркадий Волож расскажут о нём все подробности. Мы всех приглашаем.
Истории: одна о гуглере и одна — о сотруднике Яндекса
С момента создания ШАД её закончили 260 специалистов в области computer science. Мы попросили двух выпускников Школы рассказать о том, что им дало обучение в ней, и дать несколько советов тем, кто решил поступать.
Андрей Петров, разработчик в мюнхенском офисе Google.
Когда я был студентом, у меня сложилась иллюзия, что программировать я уже умею, а Computer Science — это просто. Действительно, ведь я создавал сайты с динамическим контентом, писал игры, получал призы на олимпиадах и без проблем сдавал экзамены в университете. Однако это было лишь хобби, а я был любителем. Чтобы начать путь профессионала, я пошёл в школу Яндекса.
Там я вскоре узнал, что разработка — это не написание кода, а соблюдение стиля, использование практик, поддержка документации и тестирование ПО. Там я впервые смог вплотную познакомиться с крайне актуальной наукой машинного обучения, причём как узнать о её строгих математических основаниях, так и провести множество экспериментов на настоящих данных, соревнуясь с коллегами за проценты качества. Там я расширил свой кругозор и ознакомился с отраслями, которые вызвали лишь сожаление от того, что нельзя заниматься ими всеми сразу: это распознавание образов, компьютерная лингвистика, интернет-поиск, современные алгоритмы на графах. В конце концов, там я познакомился с замечательными людьми, многие из которых впоследствии стали моими коллегами и друзьями.
Если вы раздумываете, стоит ли поступать, и пребываете в таких же иллюзиях, как я, то теперь вы знаете, что делать. Даже если никаких иллюзий нет, это всё равно крайне полезно и интересно. И в науке анализа данных, и в IT-индустрии нужны профессионалы. Чтобы примкнуть к их числу, придётся проделать немалый путь, а поступление в ШАД — это серьёзный шаг вперёд в этом направлении.
Алексей Умнов, выпускник ШАД. Разработчик в группе морфологии Поиска в Яндексе, аспирант ВМК МГУ.
В ШАДе я получил множество полезных теоретических и практических знаний. Они пригодились мне как в проектах внутри Яндекса, так и в других областях. Например, в научной деятельности я очень активно использую знания, полученные на курсе машинного обучения, а также различные навыки программирования. Стоит также отметить, что весь материал, даваемый в ШАДе, достаточно современный, что очень важно для такой быстро развивающейся области, как Computer Science.
Будущим студентам я бы посоветовал приготовиться к достаточно большой нагрузке и не совсем привычной форме обучения: чтобы получить хорошую оценку за курс, нужно на протяжении всего семестра сдавать домашние задания, и итоговой контрольной или экзамена для этого недостаточно.
Разбор вступительных задач
На этот раз мы решили впервые публично разобрать все задания письменного вступительного экзамена в Школу анализа данных. К нему допускаются только те, кто успешно справился с заданием в анкете. В прошлом году из 617 человек приглашение на него получили 284, а успешно сдали и дошли до собеседования — 132.
Задача 1
Последовательность
Найдите формулу общего члена последовательности.
Решение
Введем обозначение
Кроме того,
Отсюда получаем
Задача 2
Даём множество A = {1,2,...,n}. Среди всех его подмножеств равновероятно выбираем k его подмножеств A1,…,Ak. Найдите вероятность того, что
Решение
Рассмотрим элемент i ∈ A. Очевидно, подмножеств в A, содержащих i и не содержащих i, равное количество. Таким образом вероятность того, что i лежит в Aj равна 1/2. Эти вероятности независимы для разных j. Получаем, что вероятность того, что i содержится в
Задача 3
Дан массив длины n из нулей и единиц. Найдите в нём подмассив макисмальной длины, в котором количество единиц равно количеству нулей. Ограничения: O(n) по времени и O(n) по дополнительной памяти.
Решение
Обозначим исходный массив через a[・]. Заведём еще четыре массива длины n: b[・], c[・], d[・] и e[・]. Пройдём по возрастанию индексов и заполним массив b[・] по правилу:
Далее, когда мы прошли по всему массиву b[・], заполним массив e[・] по правилу e[i] = d[i] — c[i]. Заметим, что если в массиве a[・] есть подмассив от a[m] до a[l], в котором равное количество единиц и нулей, то b[m] = b[l] = k. И тогда c[k] — это минимальный номер i такой, что b[i] = k, а d[k] — максимальный. Соответственно, e[k] — максимальное расстояние между m и l, где b[m] = b[l] = k. Найдём максимум массива e[・]. (Очевидно, это можно сделать за O(n) операций.) пусть он равен e[j]. Тогда искомы подмассив — это подмассив от a[c[j]] до a[d[j]]
Задача 4
Пусть

Для каких m ∈ [0, 10] Im≠0?
Решение
Многократно воспользуемся формулой:
С помощью этой формулы получим:
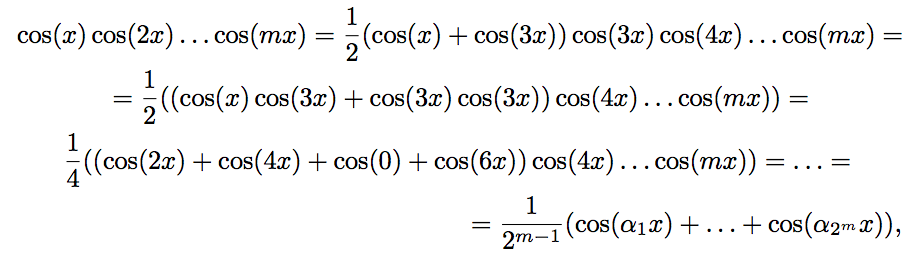 где ai = 1 ± 2 ± 3 … ± m ∈ Z. Несложно убедиться, что чётности всех чисел ai будут одинаковы. Более того, в случаях m = 4k и m = 4k + 3 все ai чётны. Если ai ≠ 0, то
где ai = 1 ± 2 ± 3 … ± m ∈ Z. Несложно убедиться, что чётности всех чисел ai будут одинаковы. Более того, в случаях m = 4k и m = 4k + 3 все ai чётны. Если ai ≠ 0, то Значит, при m = 4k + 1 и m = 4k + 2, Im = 0. Если же m = 4k или 4k + 3, то среди ai обязательно есть ноль, так как между числами 1, 2, …, m можно так расствить знаки «+» и «—», чтобы получился ноль. Действительно,
(1 + 2 − 3) + (4 − 5 − 6 + 7) +... + (4k − (4k + 1) − (4k + 2) + (4k + 3)) = 0.
Таким образом, m = 4k и 4k + 3, Im = 0. Ответ: при m = 0,3,4,7,8.
Задача 5
Дан неориентированный граф G без петель. Пронумеруем все его вершины. Матрица смежности графа G с конечным числом вершин n (пронумерованных числами от 1 до n) — это квадратная матрица A размера n, в которой значение элемента aij равно числу рёбер из i-ой вершины графа в j-ю вершину.
Докажите, что матрица A имеет отрицательное собственное значение.
Решение
Утверждение задачи не свосем верно. Если в графе нет рёбер, то матрица нулевая и все собственные значения равны нулю. Если же рёбра есть, то A — симметрическая матрица с неотрицательными элементами и нулями на диагонали. Докажем, что у такой матрицы есть неотрицательное собственное значение.
Известный факт, что симметрическая матрица диагонализуема в вещественном базисе. (Все собственные значения вещественны.) Допустим, что все собственные значения A неотрицательны. Рассмотрим квадратичную форму q с матрицей A в базисе {e1, … ,en}. Тогда эта квадратичная форма неотрицательно определена, так как все собственные значения неотрицательны. То есть
Задача 6
Рассмотрим бесконечный двумерный массив
Решение
Допустим, что
Задача 7
Дана матрица из нулей и единиц, причём для каждой строки матрицы верно следующее: если в строке есть единицы, то они все идут подряд (неразрывной группой из единиц). Докажите, что определитель такой матрицы может быть равен ±1 или 0.
Решение
Переставляя строки, мы можем добиться того, чтобы позиции первых (слева) единиц не убывали сверху вниз. При этом определитель либо не изменится, либо поменяет знак. Если у двух строк позиции первых единиц совпадают, то вычтем ту, в которой меньше единиц из той, в которой больше. Определитель при этом не меняется. Такими операциями мы можем добиться того, что позиции первых единиц строго возрастают сверху вниз. При этом либо матрица окажется вырожденной, либо верхнетреугольной с единицами на диагонали. То есть, определитель станет либо 0, либо 1. Так как определитель при наших операциях либо не менялся, либо поменял знак, изначальный определитель был ±1 или 0.
Ещё пара слов о школе
В ШАД преподают известные российские учёные. Например, курс по анализу данных разработал и ведёт Илья Мучник, профессор Rutgers University. Когда-то он был научным руководителем Аркадия Воложа. Теорию машинного обучения, без которого невозможно представить работу с большими объемами данных, преподаёт Алексей Червоненкис, профессор Лондонского университета и один из создателей отечественной школы анализа данных. Программу отделения Computer Science разрабатывал в том числе и Илья Сегалович. Мы создавали ШАД, чтобы вырастить поколение программистов, которые могут применять академические знания в прикладных задачах. Поэтому у нас преподают не только учёные, но и сотрудники Яндекса.
В прошлом году мы получили 617 заявок на поступление, 284 человека были приглашены на письменный экзамен. Но это не последнее испытание для поступающих в Школу. По результатам экзамена мы приглашаем на собеседования. Из 132 человек, которые его успешно сдали и дошли до собеседований, на первый курс было зачислено 97 человек.
Как многие из вас могут помнить, ШАД появилась в 2007 году. Сейчас у нас есть филиалы в Екатеринбурге, Киеве, Минске и Новосибирске. В Санкт-Петербурге отделение ШАД открыто при Computer Science Center.
Обучение на курсах длится два года. Программа разделена на три типа курсов: теоретические («Дискретный анализ», «Комбинаторика», «Вероятность», «Теория сложности»), практические («Обучение программированию на С++», «Java», «Параллельные и распределенные вычисления») и смешанные («Алгоритмы и структуры данных», «Машинное обучение», «Компьютерная лингвистика» и т.д.). Учиться можно и на заочном отделении, общаясь с преподавателями по электронной почте и пользуясь видеолекциями.

 Когда я был студентом, у меня сложилась иллюзия, что программировать я уже умею, а Computer Science — это просто. Действительно, ведь я создавал сайты с динамическим контентом, писал игры, получал призы на олимпиадах и без проблем сдавал экзамены в университете. Однако это было лишь хобби, а я был любителем. Чтобы начать путь профессионала, я пошёл в школу Яндекса.
Когда я был студентом, у меня сложилась иллюзия, что программировать я уже умею, а Computer Science — это просто. Действительно, ведь я создавал сайты с динамическим контентом, писал игры, получал призы на олимпиадах и без проблем сдавал экзамены в университете. Однако это было лишь хобби, а я был любителем. Чтобы начать путь профессионала, я пошёл в школу Яндекса. В ШАДе я получил множество полезных теоретических и практических знаний. Они пригодились мне как в проектах внутри Яндекса, так и в других областях. Например, в научной деятельности я очень активно использую знания, полученные на курсе машинного обучения, а также различные навыки программирования. Стоит также отметить, что весь материал, даваемый в ШАДе, достаточно современный, что очень важно для такой быстро развивающейся области, как Computer Science.
В ШАДе я получил множество полезных теоретических и практических знаний. Они пригодились мне как в проектах внутри Яндекса, так и в других областях. Например, в научной деятельности я очень активно использую знания, полученные на курсе машинного обучения, а также различные навыки программирования. Стоит также отметить, что весь материал, даваемый в ШАДе, достаточно современный, что очень важно для такой быстро развивающейся области, как Computer Science.