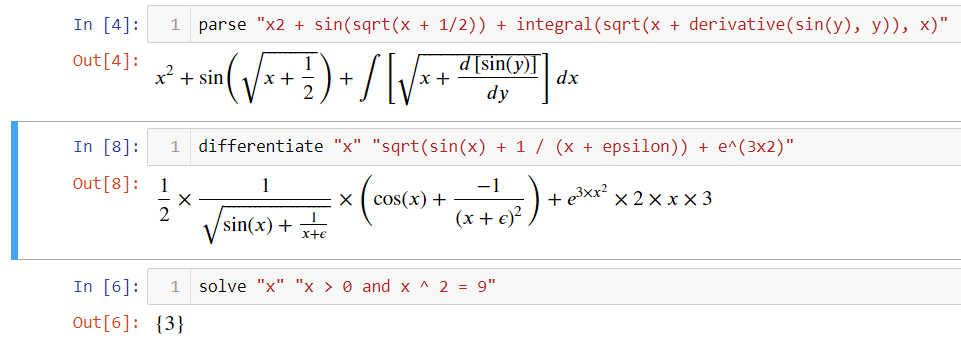
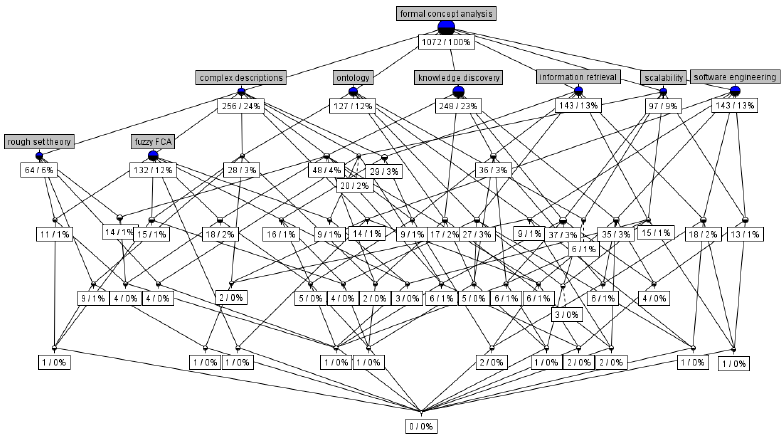
There is one only too obvious problem with relativity of simultaneity in the way it is normally introduced, and I have never found an answer to it – what’s more, I never read or heard anyone formulate it. I will be grateful for an enlightening discussion.
The framework of the thought experiment introducing relativity of simultaneity is this. Two rays of light travel in opposite directions and reach their destination simultaneously in one frame of reference and at different moments in the other.
For example, in the Wikipedia article on the subject you can read:
‘A flash of light is given off at the center of the traincar just as the two observers pass each other. For the observer on board the train, the front and back of the traincar are at fixed distances from the light source and as such, according to this observer, the light will reach the front and back of the traincar at the same time.
‘For the observer standing on the platform, on the other hand, the rear of the traincar is moving (catching up) toward the point at which the flash was given off, and the front of the traincar is moving away from it. As the speed of light is finite and the same in all directions for all observers, the light headed for the back of the train will have less distance to cover than the light headed for the front. Thus, the flashes of light will strike the ends of the traincar at different times’.
I am always not a little surprised at the modesty displayed by the authors of such illustrations. If we grant the statement ‘the light headed for the back of the train will have less distance to cover than the light headed for the front’ to be true – how then do we evaluate the magnitude of the effect? Or, in other words, how much longer is one distance in comparison to the other?