Методы применения алгоритма нахождения максимального потока в сети

Введение

Задача о максимальном потоке является классической и имеет множество применений. Напомню постановку проблемы. Дан взвешенный ориентированный граф с неотрицательными весами (пропускными способностями). Выделены две вершины: исток S и сток T такие, что любая другая вершина лежит на пути из S в T. Потоком назовем функцию F: V x V с такими свойствами

1. Ограничение пропускной способности. Поток по ребру не может быть больше его (ребра) пропускной способности.
2. Антисимметричность. Для каждого ребра (u, v): F(u, v) = -F(v, u).
3. Сохранение потока. Для каждой вершины (кроме S и T), количество входящего потока (отрицательного) равен количеству исходящего потока (положительного). Тоесть, алгебраическая сумма потоков для каждой вершины (кроме S и T) равна нулю.

В этом посте вы можете ознакомиться с реализацией поставленной проблемы.

Перейдем непосредственно к типичным задачам, которые сводятся к алгоритму нахождения максимального потока в сети. Часто выявить в таких задачах поток очень не просто.

Задачи

1. Задача о максимальном паросочетании. На вход дается N — количество мальчиков, M — количество девочек и список, какой мальчик с какой из девочек хочет танцевать (таких может быть несколько). Надо определить максимальное количество одновременно танцующих пар.
   
   
   

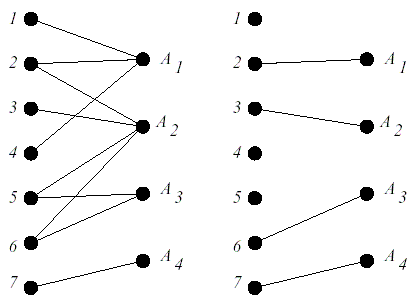
   Решение

   
   Для решения этой задачи можно использовать алгоритм Куна, но раз уж мы взялись сводить все к потоку — давайте это сделаем. Для этого не хватает истока и стока. Давайте их добавим! «Слева» добавим фиктивную вершину и проведем ребра ко всем мальчикам весом в 1. От мальчиков к девочкам уже есть ребра проставим им тоже цену 1. И от девочек ребра к стоку тоже ценой 1. Ответом к задаче является величина максимального потока между истоком и стоком.
2. Испорченный паркет. У паркета NxM, некоторые клетки могут быть испорчены. Их необходимо закрыть новыми плитками. Плитки бывают размером 2х1 (можно поворачивать, но нельзя разрезать) ценой А, и 1х1 ценой B. Спрашивается, какую минимальную сумму нужно потратить, что бы заложить испорченные плитки паркета. Естественно, новые плитки не должны перекрывать никакие другие плитки.
   
   

   Решение

   
   Для начала, убедимся, что 2*B>A. Иначе, все выгодней замостить только плитками 1х1 и больше нечего считать. Далее наша задача максимизировать количество плиток ценой А.
   Раскрасим наш паркет по принципу шахматной доски. Очевидно, что тогда один конец плитки 2х1 будет лежать на черной клетке, другой — на белой. Итак, построим двудольный граф, одна доля которого будет содержать белые клетки, другая — черные. Ребра весом в 1 проведем между граничащими клетками. Добавим исток с ребрами в белые вершины весом в бесконечность (довольно распространенный прием) и сток с ребрами из черных клеток весом тоже в бесконечность. Пускай f — величина найденного максимального потока между истоком и стоком. Тоесть мы нашли количество плиток 2х1. Ответом к задаче будет величина f*A+(K-f)*B, где K — общее количество испорченных клеток.
   Источник: Харьковская зимняя школа по программированию, 2009, День 3
   
3. Задача живопись. Дана матрица N*M с клетками, покрашенными либо в черный, либо в белый цвета. W — цена перекраски черного квадрата в белый, B — белого в черный. После перекраски, между всеми соседними квадратами разных цветов нужно провести серую линию, ценой G. Надо так отпимально перекрасить матрицу (или ничего не делать), что бы потратить минимальную сумму.
   
   
   

   Решение

   
   Крайний случай: если матрица вся одного цвета — ответ 0.
   Добавим фиктивные исток и сток. От истока ко всем белым вершинам проведем ребра, весом в B (цена перекраски в черный). От черных вершин ко стоку проведем ребра, весом в W (цена перекраски в белый). И между всеми соседними вершинами (будь они одного или разных цветов) — ставим ребро весом в G (серая линия). Величина максимального потока будет ответом на задачу.
   Источник: Всеукраинская школьная олимпиада по информатике, 2007, День 1
   
4. Задача с ограничением на вершины. Пусть надо найти величину максимального потока и на вершины наложено ограничение, сколько они могут пропустить.
   
   

   Решение

   
   Все, что нам надо — это разделить каждую вершину на две, и между ними поставить ребро, весом в ограничение пропускной способности данной вершины
5. Минимальный разрез. Дан граф. Сколько вершин надо удалить, что бы не существовало пути из A в B?
   
   

   Решение

   
   В классической задаче о минимальном разрезе удалять нужно ребра. Не проблема! Разобьем вершины на 2, и поставим между ними ребро, весом в 1. Тогда ответ к задаче — нахождение минимального разреза в графе (что и есть максимальным потоком).
   Источник: Харьковская зимняя школа по программированию, 2009, День 3
   
6. Сочинитель стихов. Имеется детерминированный конечный автомат с одним начальным состоянием A и одним конечным B. Каждый переход задается тройкой чисел (i, j, k), переход из состояния i в состояние j по ребру k.
   После перехода по автомату из i в j по ребру k, стираются все переходы из i по ребру k, а также все переходы в j по ребру k. Требуется вывести количество путей из A в B по такому автомату.
   
   

   Решение

   
   Задача сводится к нахождению максимального количества путей, причем из одной вершины не выходят более одного ребра одного цвета. Сведем задачу к нахождения максимального потока. Для каждой вершин создадим k+1 вершину в перестроенной сети. Первая вершина будет входом, остальные вершины будут представлять цвета. Из вершины входа проведем по ребру пропускной способностью 1 в каждую из k вершин, соответствующих цвету. Из вершины соответствующих цвету i проведем все ребра цвета i во входы концов ребер. Найдя максимальный поток в такой сети, получим максимальное количество путей удовлетворяющих требуемому свойству.
   Источник: Харьковская зимняя школа по программированию, 2009, День 4
   
7. Коллекционирование монет. Есть n коллекционеров и m видов монет. Для вступления в клуб, необходимо иметь не меньше одной монеты каждого типа. Вы (у Вас номер 1) можете меняться с коллекционерами имеющимися монетами. Любой коллекционер обменяет монету свою монету a на Вашу монету b, если у него больше одной монеты типа a и нету ни одной монеты типа b. Вы, в свою очередь, можете нарушать это правило. Нужно набрать как можно больше типов монет по известной ситуации у всех коллекционеров.
   
   

   Решение

   
   Построим сеть. Создадим для каждого типа монет по одной вершине. Эти вершины будут соответствовать Вашим монетам. Нужно собрать как можно больше уникальных монет, поэтому проведем ребро пропускной способности 1 в сток из каждой такой вершины. В вершины, соответствующие монетам, которые у Вас есть изначально, проведем ребро, пропускная способность которого равна количеству таких монет у Вас.
   Для каждого члена клуба (кроме 1, тоесть Вас) заведем по одной вершине. Эта вершина может принимать не более одной монеты, которой у него нет и отдавать
   не более k-1 монеты, которых у него k (k > 1). Естественно, член клуба отдает одну монету взамен одной полученной.
   Таким образом, в каждую такую вершину нужно провести ребро пропускной способности 1 из вершин соответствующих монетам, которых нет у этого члена клуба. А из этих вершин нужно провести ребра пропускной способностью k_i — 1 в вершину i, соответствующую монетам, которых у члена клуба больше одной.
   Построенная сеть отражает процессы обмена в клубе. Максимальный поток в такой сети будет равен максимальному количеству монет, которые могуть быть собраны Вами.
   Источник: Харьковская зимняя школа по программированию, 2009, День 4
   
8. Циркуляция. Система охлаждения реактора представляет собой набор труб, соединяющих узлы. По трубам течет жидкость, причем для каждой трубы строго определено направление, в котором она должна по ней течь. Узлы системы охлаждения занумерованы от 1 до N. Система охлаждения должна быть спроектирована таким образом, чтобы для каждого узла за единицу времени количество жидкости, втекающей в узел, было равно количеству жидкости, вытекающей из узла. У каждой трубы имеется пропускная способность c_ij. Кроме того, для обеспечения достаточного охлаждения требуется, чтобы по трубе протекало не менее l_ij единиц жидкости за единицу времени. То есть для трубы, ведущей из i-го узла в j-ый должно выполняться l_ij ≤ f_ij ≤ c_ij.
   Дано описание системы охлаждения. Нужно выяснить, каким образом можно пустить жидкость по трубам, чтобы выполнялись все указанные условия.
   
   

   Решение

   
   Это задача на нахождение циркуляции в сети с заданными нижними ограничениями на ребра. Если по ребру (u, v) должен проходить поток в отрезке [l, r], то в перестроенной сети будет три ребра (откуда, куда, вес): (u, v, r — l), (S, v, l), (u, T, l). S, T — дополнительно введенные сток и исток соответственно. Фактически мы пропускаем по ребру необходимый минимальный поток, после чего балансируем его так, чтобы получить циркуляцию.
   Источник: Харьковская зимняя школа по программированию, 2009, День 4
   
9. Снова танцы. На вечеринку приглашены n мальчиков и n девочек. Они хотят станцевать несколько раундов.
   В каждом раунде гости делятся на n танцующих пар. Каждый гость должен быть в некоторой паре, каждая пара должна состоять из одного мальчика и одной девочки. В каждом раунде каждый мальчик должен танцевать с другой девочкой. Некоторые мальчики и девочки не нравятся друг другу. Каждый мальчик может танцевать не более чем с k девочками, которые ему не нравятся. Аналогично каждая девочка может танцевать не более чем с k мальчиками, которые ей не нравятся.
   Имеется информация о том, нравятся ли друг другу i-ый мальчик и j-ая девочка (1 ≤ i, j ≤ n). Найти наибольшее количество раундов, которое можно станцевать на вечеринке.
   
   

   Решение

   
   Рассмотрим следующую задачу: могут ли танцы продолжаться в точности m раундов? Если мы сможем ответить на этот вопрос, то бинарным поиском найдем наибольшее m, для которого проведение танцев возможно.
   Построим граф, имеющий один исток и один сток (черные вершины). Красные вершины представляют мальчиков, серые – девочек. Если мальчик и девочка нравятся друг другу, то проведем между ними ребро единичной пропускной способности (на рисунке такими являются два ребра – верхнее и нижнее). Иначе добавим синие и зеленые вершины как показано на рисунке и установим пропускную способность ребер между соответствующими синими и зелеными вершинами равную 1.
   Синие и зеленые вершины образуют “защитный” уровень. Связь мальчиков с девочками, которые друг другу не нравятся, будет проходить по ребрам защитного уровня. Каждый мальчик может танцевать не более чем с k девочками, которые ему не нравятся. Установим пропускную способность ребер между красными и синими, зелеными и серыми вершинами равную k. Таким образом, между каждым мальчиком и каждой девочкой будет установлена связь через ребро либо напрямую, либо через вершины защитного уровня.
   Танцы должны продолжаться в точности m раундов. Установим пропускную способность ребер между истоком и красными вершинами, а также между серыми вершинами и стоком равную m.
   
   Находим максимальный поток в графе. Танцы могут продолжаться в точности m раундов тогда и только тогда, когда величина максимального потока будет равна n * m, где n – количество мальчиков.
   Источник: Севастопольская летняя школа по программированию, 2010, День 4
   

Заключение

Мы рассмотрели ничтожно малую часть необъятного множества задач, сводящихся к нахождению максимального потока в сети. И это не затрагивая максимальный поток минимальной стоимости. Такие задачи отличаются своей красотой в решении. Программисту, зная стандартный алгоритм нахождения максимального потока, остается только построить граф, соответствующий поставленной задаче и пустить поток.