 Думаю, многие знакомы с весьма необычной игрой Minecraft (справа — пример сгенерированной в ней карты), в которой игрок находится на (практически) бесконечной поверхности Земли и может исследовать окружающий мир с минимальными ограничениями.
Думаю, многие знакомы с весьма необычной игрой Minecraft (справа — пример сгенерированной в ней карты), в которой игрок находится на (практически) бесконечной поверхности Земли и может исследовать окружающий мир с минимальными ограничениями.Как же автору игры, Notch'у, удалось добиться подобного сходства его случайных «миров» с земными просторами? В этом топике я как раз и рассмотрю один из способов построить искусственный ландшафт такого рода (и вскользь упомяну пару других способов), а также расскажу о моем небольшом усовершенствовании этого алгоритма, позволяющем значительно увеличивать размеры ландшафта без заметных потерь в производительности.
Внутри вас ждет несколько схем и красивых картинок, довольно много букв и ссылка на пример реализации алгоритма.
Общий план действий
Что же в целом подразумевается под генерацией ландшафта? Если говорить о создании (почти в реальном времени) уровня для компьютерной игры — такой как, собственно, Minecraft, то этот процесс состоит из следующих пунктов:
- Создание карты высот. Изначально у нас есть плоская двумерная сетка и каждой её клетке мы присваиваем некоторую высоту. Каким образом? Об этом и пойдет речь далее. Кстати, сетка не обязательно должна быть прямоугольной — например, здесь описан аналогичный алгоритм для сетки, состоящей из треугольников. Тем не менее, в большинстве случаев удобнее сетка, состоящая из квадратных ячеек-пикселей. Вместе с картой высот задаются и области, покрытые водой — как минимум, моря и океаны (как правило, водой становятся просто те клетки, которые лежат ниже определенного уровня).
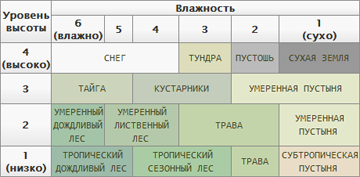
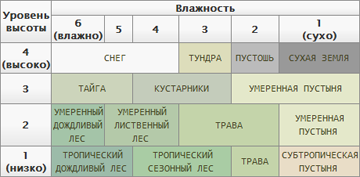 Распределение биомов. Тут понадобятся некоторые знания в географии (впрочем, весь процесс создания ландшафта этого требует). Определить, где должна быть тундра, где пустыня, а где тропический лес — поможет уже созданная карта высот и, например, расстояние от водных пространств или до некоторых предопределенных точек (экватор/полюса). В свою очередь, биомы зададут многие другие параметры — например, травяной покров, количество каменистых участков, растения, количество рек и озер и т.д.
Распределение биомов. Тут понадобятся некоторые знания в географии (впрочем, весь процесс создания ландшафта этого требует). Определить, где должна быть тундра, где пустыня, а где тропический лес — поможет уже созданная карта высот и, например, расстояние от водных пространств или до некоторых предопределенных точек (экватор/полюса). В свою очередь, биомы зададут многие другие параметры — например, травяной покров, количество каменистых участков, растения, количество рек и озер и т.д.- Землю мы создали, океаны и моря тоже, географические зоны распределили. Что забыли? Пустить реки, конечно же! Кроме собственно вод, которые будут течь с гор и спускаться в моря или образовывать озера в ложбинах, следует проэмулировать их воздействие на поверхность земли — образовать русла рек и произвести перенос песка и мягкого грунта по течению с образованием пляжей на берегах озер и других водоемов. К сожалению, этот процесс, называемый водной эрозией, как и другие виды эрозий, я вынужден оставить за рамками данной статьи. Тем не менее, в списке использованной литературы есть пара ссылок на очень хорошие материалы по этой теме.
- Дополнительные действия. Фактически, ландшафт уже создан, но есть ещё много вещей, которые можно на нем улучшить — например, в Minecraft пространство под землей сплошь изрыто естественными пещерами, а на поверхности растет множество деревьев. Кроме того, разумеется, в зависимости от биомов можно разнообразить флору и фауну — если ставится целью максимально приблизиться к тому, что происходит в настоящей природе.
Наконец, сгенерированный ландшафт останется только отрисовать. Здесь хочется заметить только одну деталь — в то время как упомянутая выше треугольная сетка оказалась бы кстати при традиционной визуализации трехмерной карты, для квадратных ячеек очень кстати может оказаться использование вокселей. Впрочем, это уже совсем другая история.
Способы построения карты высот
Итак, займемся самым важным этапом построения ландшафта — определением того, на какой высоте находится каждая точка поверхности земли. Самая банальная идея — пробежаться по обоим координатам и сделать map[x][y] = random() — как ни странно, не даст приемлемых результатов, поэтому нужно использовать кое-что похитрее.
Создание холмов «вручную»
Довольно простой алгоритм: изначально считаем, что все точки находятся на одном уровне и начинаем добавлять в произвольных местах эдакие «выпуклости» — холмы различной высоты. В результате аккуратного наложения этих холмов друг на друга (и, возможно, добавления небольшого шума, упомянутого выше) уже можно получить нечто похожее на правду. Но куда более реалистичных ландшафтов можно достичь перечисленными ниже алгоритмами, поэтому на методе «холмов» я не буду останавливаться.
Ландшафт на базе диаграммы Вороного
На самом деле, до недавнего времени следующий подход для меня был совершенно неизвестен и я был весьма удивлен тем, что он способен давать весьма впечатляющие результаты.
 Начинается всё со случайного бросания точек на карту. Затем по этим точкам строится диаграмма Вороного (и, соответственно, триангуляция Делоне), а на ней выполняется несколько итераций релаксации Ллойда, чтобы избавиться от слишком мелких полигонов.
Начинается всё со случайного бросания точек на карту. Затем по этим точкам строится диаграмма Вороного (и, соответственно, триангуляция Делоне), а на ней выполняется несколько итераций релаксации Ллойда, чтобы избавиться от слишком мелких полигонов.Если вам оказался непонятен предыдущий абзац — не страшно, его суть сводится к созданию примерно такой сетки, как на рисунке справа. Главное её свойство — это её нерегулярность. Это позволяет построенному на её основе ландшафту не выглядеть слишком «квадратным».
 Дальнейшие действия тривиальны — мы случайным образом выбираем полигоны, подлежащие заполнению водой, а высоту точек, принадлежащих остальным полигонам, делаем равной кратчайшему расстоянию до моря-окияна. Осталось добавить всё тот же шум (причем как к собственно высоте, так и к границам полигонов) — и мы получим весьма симпатичный остров (или материк, в зависимости от масштабов).
Дальнейшие действия тривиальны — мы случайным образом выбираем полигоны, подлежащие заполнению водой, а высоту точек, принадлежащих остальным полигонам, делаем равной кратчайшему расстоянию до моря-окияна. Осталось добавить всё тот же шум (причем как к собственно высоте, так и к границам полигонов) — и мы получим весьма симпатичный остров (или материк, в зависимости от масштабов).Реализацией данного алгоритма я не занимался и для упрощения статьи опустил несколько деталей и промежуточных. С подробной статьей (из которой были позаимствованы картинки и большая часть информации), можно ознакомиться по ссылке (на английском), там же есть замечательное swf-демо, крайне наглядно иллюстрирующее все этапы процесса.
Алгоритм diamond-square
Самым же распространенным и дающим одни из самых реалистичных результатов является алгоритм diamond-square (или square-diamond), расширение одномерного алгоритма midpoint displacement на двумерную плоскость. Ландшафты, получающиеся с его помощью, как правило, называют фрактальными, хотя, следует признать, на самом деле они не так уж самоподобными — напротив, как мы увидим ниже, их не очень приятным свойством является то, что в крупном масштабе они становятся относительно гладкими, а в мелком превращаются в подобие наждачной бумаги.

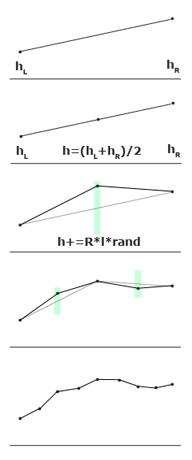 Начнем с более простого алгоритма midpoint displacement. Как уже сказано, он работает не на двумерной плоскости, а на одномерном отрезке (поэтому с его помощью можно, например, создать линию горизонта).
Начнем с более простого алгоритма midpoint displacement. Как уже сказано, он работает не на двумерной плоскости, а на одномерном отрезке (поэтому с его помощью можно, например, создать линию горизонта).То, что роднит этот алгоритм с фракталами — это его рекурсивное поведение. Изначально мы любым образом задаем высоту на концах отрезка и разбиваем его точкой посередине на два под-отрезка. Эту точку мы смещаем на случайную величину и повторяем разбиение и смещение для каждого из полученных под-отрезков. И так далее — пока отрезки не станут длиной в один пиксель. Вот и весь алгоритм (см. рисунок справа). Ах, да — важное замечание: случайные смещения должны быть пропорциональны длинам отрезков, на которых произведятся разбиения. Например, мы разбиваем отрезок длиной l — тогда точка посередине него должна иметь высоту
h = (hL + hR) / 2 + random(- R * l, R * l)
(hL и hR — высоты на левом и правом конце отрезка, а константа R определяет «шероховатость» (roughness) получающейся ломаной и является главным параметром в данном алгоритме).
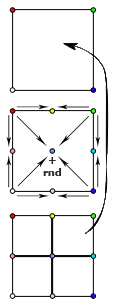 Попробуем обобщить этот алгоритм для двумерной карты высот. Начнем с присвоения случайных высот четырем углам всей карты целиком и разобъем её (для удобства я предполагаю, что мы работаем с квадратной картой, причем её сторона является степенью двойки) на четыре равных квадрата. В каждом из них известно значение в одном из углов. Где взять остальные?
Попробуем обобщить этот алгоритм для двумерной карты высот. Начнем с присвоения случайных высот четырем углам всей карты целиком и разобъем её (для удобства я предполагаю, что мы работаем с квадратной картой, причем её сторона является степенью двойки) на четыре равных квадрата. В каждом из них известно значение в одном из углов. Где взять остальные?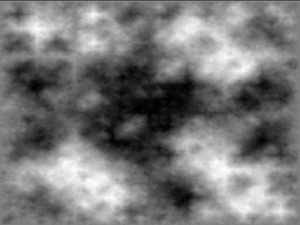
Всё той же интерполяцией, как и в одномерном midpoint displacement — точка в центре получается усреднением высот всех 4 угловых точек, а каждая серединная точка на стороне большого квадрата — усреднением пары точек, лежащих на концах соответствующей стороны. Осталось привнести немного шума — сдвинуть случайным образом центральную точку вверх или вниз (в пределах, пропорциональных стороне квадрата) — и можно повторять рекурсивно наши действия для полученных под-квадратиков. Всё? Всё, да не всё.
Это ещё не diamond-square — данный алгоритм, как правило, тоже называют алгоритмом midpoint displacement и несмотря на то, что он дает уже относительно приемлимые результаты, в получившейся картинке без особого труда можно заметить её «прямолинейную» натуру.
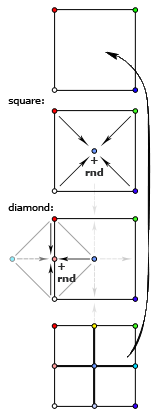 Алгоритм diamond-square — тот самый, который позволяет получать «настоящие» фрактальные ландшафты — отличается от двумерного midpoint displacement тем, что состоит из двух шагов. Первый — т. н. «square» — точно так же определяет центральную точку в квадрате путем усреднения угловых и добавлением собственно displacement'а — случайного отклонения. Второй же шаг — «diamond» — призван определить высоту точек, лежащих на серединах сторон. Здесь усредняются не две точки — «сверху» и «снизу» (если говорить о точках на вертикальной стороне), но и пара точек «слева» и «справа» — то есть еще две полученных на шаге «square» центральных точки. Важно заметить, что эти две высоты, которые достались нам на предыдущем шаге, должны быть уже посчитаны — поэтому обсчет нужно вести «слоями», сначала для всех квадратов выполнить шаг «square» — затем для всех ромбов выполнить шаг «diamond» — и перейти к меньшим квадратам.
Алгоритм diamond-square — тот самый, который позволяет получать «настоящие» фрактальные ландшафты — отличается от двумерного midpoint displacement тем, что состоит из двух шагов. Первый — т. н. «square» — точно так же определяет центральную точку в квадрате путем усреднения угловых и добавлением собственно displacement'а — случайного отклонения. Второй же шаг — «diamond» — призван определить высоту точек, лежащих на серединах сторон. Здесь усредняются не две точки — «сверху» и «снизу» (если говорить о точках на вертикальной стороне), но и пара точек «слева» и «справа» — то есть еще две полученных на шаге «square» центральных точки. Важно заметить, что эти две высоты, которые достались нам на предыдущем шаге, должны быть уже посчитаны — поэтому обсчет нужно вести «слоями», сначала для всех квадратов выполнить шаг «square» — затем для всех ромбов выполнить шаг «diamond» — и перейти к меньшим квадратам.Объяснения, думаю, могут показаться запутанными, поэтому советую внимательно изучить приложенные схемы — по ним должно стать яснее, высоты каких точек вычисляются на каждом этапе.
Кроме необходимости использовать, скажем так, обход в ширину вместо обхода в глубину, есть ещё одна тонкость — ситуация на краях ландшафта. Дело в том, что на этапе «diamond» алгоритм использует высоту точек, которых находятся за пределами текущего квадрата и, возможно, всей карты. Как быть? Варианта два (хотя вы можете придумать и свой собственный, конечно): либо считать эти высоты равными 0 (или 1, или любой другой константе; это, кстати, удобно для погружения краев нашего ландшафта под воду), либо представить что наша плоскость свернута в тор (тороидальная планета, хм...) и пытаясь узнать высоту точки, лежащей на 64 пикселя левее левой границы карты, мы узнаем высоту точки, отстоящей на 64 точки от правой границы. Реализуется очень просто (как, впрочем, и первый вариант) — нам поможет взятие координат по модулю, равному размеру карты.
 Итак, таковы основные алгоритмы построения карт высот для искусственно генерируемых ландшафтов. На мой взгляд, наиболее реалистичные результат дает последний из них, diamond-square — хотя и он не лишен некоторых недостатков. Например, создав карту, которая хорошая выглядит при сильном приближении — при просмотре целиком вы увидите множество мелких островков (а то и вовсе сплошной шум, с которого мы начинали) вместо нескольких больших материков и океанов. Самоподобия не выходит. Исправить это можно различным комбинированием фрактальных ландшафтов разного масштаба. Их значения можно перемножать, складывать, использовать различные коэффициенты или, например, привнести данные, полученные с помощью диаграммы Вороного — в общем, простор для экспериментов достаточно велик. Кстати, даже используя только один diamond-square, полученные значения (предварительно нормализованные, то есть в диапазоне от 0.0 до 1.0) полезно возвести в квадрат — это сделает равнины более пологими, а склоны гор более крутыми (помните про эрозию?).
Итак, таковы основные алгоритмы построения карт высот для искусственно генерируемых ландшафтов. На мой взгляд, наиболее реалистичные результат дает последний из них, diamond-square — хотя и он не лишен некоторых недостатков. Например, создав карту, которая хорошая выглядит при сильном приближении — при просмотре целиком вы увидите множество мелких островков (а то и вовсе сплошной шум, с которого мы начинали) вместо нескольких больших материков и океанов. Самоподобия не выходит. Исправить это можно различным комбинированием фрактальных ландшафтов разного масштаба. Их значения можно перемножать, складывать, использовать различные коэффициенты или, например, привнести данные, полученные с помощью диаграммы Вороного — в общем, простор для экспериментов достаточно велик. Кстати, даже используя только один diamond-square, полученные значения (предварительно нормализованные, то есть в диапазоне от 0.0 до 1.0) полезно возвести в квадрат — это сделает равнины более пологими, а склоны гор более крутыми (помните про эрозию?).Модификация алгоритма diamond-square для больших карт
Ну и напоследок — несколько слов о моей реализации алгоритма diamond-square. Главный вопрос, которым задаешься при генерации ландшафта — как сделать так, чтобы можно было значительно увеличить его размеры? Стандартная реализация обсуждаемого алгоритма позволяет легко увеличивать детализацию (двигаться «вглубь»), но не размеры («вширь»).
Данная проблема была решена мною следующим образом. Не знаю — возможно, это решение окажется общеизвестным или вполне очевидным для кого-то — но до этого я с ним не сталкивался и придумать его получилось не сразу (более того — «на пустом месте» возникла одна неожиданная заминка, которую разрешить «правильно» так и не удалось — об этом ниже).
Итак, подход таков: пусть наш ландшафт изначально задуман гигантских размеров (например, 16777216x16777216 пикселей, хотя это далеко не предел). Важно то, что мы не собираемся узнавать высоту в каждой точке, а вместо этого у нас будет некое значительно меньшее «окно» (например, 128x128 пикселей), которое мы будем по необходимости перемещать над нашей картой высот. Оказывается, исходный алгоритм легко модифицируется так, что нам будет требоваться на просчет «окна» число операций, пропорциональное размеру окна, но мало зависящее от размера ландшафта. Именно поэтому мы можем изначально задать ландшафт почти сколь угодно большим.
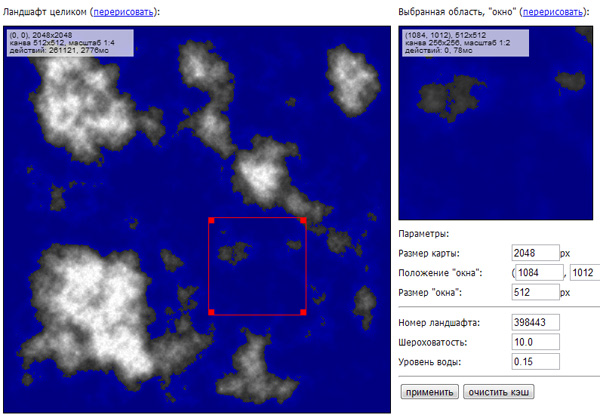
На помощь нам придет методика под названием ленивая динамика. Тем, кто знает, о чем речь, думаю, уже стало всё понятно, для несведущих в вопросе поясню. Мы «выворачиваем» весь процесс наизнанку — вместо того, чтобы начинать с больших квадратов и спускаться вниз к каждому пикселю, мы принимаем запрос вида «узнать высоту в точке (x, y)» и дальше поднимаемся вверх: наша точка, как мы знаем, была получена усреднением четырех других точек и случайным сдвигом. Самое сложное — понять, какими были эти 4 точки. После того, как мы это поймем, нам будет достаточно повторить запрос «узнать высоту», но уже для каждой из этих точек. Эти запросы, в свою очередь, поднимутся еще на уровень выше — и так далее, пока не дойдут до самого верха, до угловых точек карты (у меня они, как и точки за пределами карты, равны 0.0). В исходнике всё это выглядит примерно так:
function val(x, y, v) {
if (typeof(v) != 'undefined')
data[x + '_' + y] = Math.max(0.0, Math.min(1.0, v));
else {
if (x <= 0 || x >= size || y <= 0 || y >= size) return 0.0;
if (data[x + '_' + y] == null) {
// К этому блоку мы ещё вернемся ниже.
base = 1;
while (((x & base) == 0) && ((y & base) == 0))
base <<= 1;
if (((x & base) != 0) && ((y & base) != 0))
squareStep(x, y, base);
else
diamondStep(x, y, base);
}
return data[x + '_' + y];
}
}
function displace(v, blockSize, x, y) {
return (v + (randFromPair(x, y, seed) - 0.5) * blockSize * 2 / size * roughness);
}
function squareStep(x, y, blockSize) {
if (data[x + '_' + y] == null) {
val(x, y,
displace((val(x - blockSize, y - blockSize) +
val(x + blockSize, y - blockSize) +
val(x - blockSize, y + blockSize) +
val(x + blockSize, y + blockSize)) / 4, blockSize, x, y));
}
}
function diamondStep(x, y, blockSize) {
if (data[x + '_' + y] == null) {
val(x, y,
displace((val(x - blockSize, y) +
val(x + blockSize, y) +
val(x, y - blockSize) +
val(x, y + blockSize)) / 4, blockSize, x, y));
}
}
Главное — на ходу запоминать (и складывать в какой-нибудь кэш) все значения высот, которые мы уже вычислили. Это позволит нам не заниматься одним и тем же много раз. Собственно, даже вычислив первую точку в нашем «окне», мы попутно узнаем и ряд других точек, тоже принадлежащих этому «окну». По сути, пробежавшись по всем точкам «окна», мы сделаем не так много лишних операций — хотя их точное количество сильно зависит от того, было ли выравнено «окно» (его верхний левый угол и размер) по степеням двойки.
Как уже было сказано, в алгоритме есть несколько магических строк — вот они:
base = 1;
while (((x & base) == 0) && ((y & base) == 0))
base <<= 1;
if (((x & base) != 0) && ((y & base) != 0))
squareStep(x, y, base);
else
diamondStep(x, y, base);Здесь определяется, является ли текущая точка центром квадрата или ромба и каков размер этой фигуры. Если честно — данный код был написан просто по наитию, его точное математическое обоснование я дать не могу. Мы просто находим наименее значащий бит, который отличен от нуля хотя бы у одной из координат — он и будет искомым размером. А чтобы определить, была ли фигура квадратом — проверяем, что у обоих координат был выставлен этот бит. Обе координаты здесь нуль-индексированные.
И, наконец, неожиданный подводный камень: генератор псевдослучайных чисел. В моем коде к нему предъявлялись необычные требования: для каждой точки (x, y) всегда хочется получать одно и то же случайное число, и делать это быстро. Многие языки программирования в генераторе случайных чисел имеют возможность указать т.н. «зерно» (seed), от которого будет зависеть вся следующая последовательность генерируемых чисел (в JavaScript этого нет, но для него есть реализация распространенного вихря Мерсенна). Проблема в том, что последовательность нас не устраивает — при сдвиге окна (и очистке кэша) мы подойдем к одной точке совсем с другой стороны и случайный сдвиг станет иным. Мы же хотим статичный ландшафт, при каких бы условиях мы его ни рассматривали. Попытка инициализировать вихрь Мерсенна каждый раз «зерном», зависящим от обоих координат, провалилась: его инициализация длится слишком долго.
После некоторых размышлений я пришел к выводу, что быстрого способа преобразовать две координаты в число, которое было бы мало скоррелировано с ними, в принципе невозможно. В итоге я остановился на такой функции, которая дает приемлимые результаты из-за многократного взятия чисел по простым модулям:
function randFromPair(x, y) {
for (var i = 0; i < 80; i++) {
var xm7 = x % 7;
var xm13 = x % 13;
var xm1301081 = x % 1301081;
var ym8461 = y % 8461;
var ym105467 = y % 105467;
var ym105943 = y % 105943;
y = x + seed;
x += (xm7 + xm13 + xm1301081 + ym8461 + ym105467 + ym105943);
}
return (xm7 + xm13 + xm1301081 + ym8461 + ym105467 + ym105943) / 1520972.0;
}Кроме того, в эту функцию удалось без труда привнести «глобальное зерно», определяющее весь ландшафт целиком, а из-за взятия остатков её возращаемые значения оказались достаточно равномерно распределены по диапазону [0, 1). Впрочем, я уверен, что можно придумать более быстрое элегантное решение — можете считать это «домашним заданием» в данной статье :)
Как уже все, наверное, догадались, реализацию я написал на JavaScript, что позволяет одинаково легко поэкспериментировать как со значениями, так и с исходным кодом. Собственно страница доступна по адресу http://denull.ru/exp/diamond-square/, а весь код расположился в файле http://denull.ru/exp/diamond-square/terrain.js. Для просмотра потребуется браузер, поддерживающий html5 (скажу честно — тестировал только в Google Chrome), поскольку отрисовка идет в canvas (и, надо заметить, на собственно отрисовку тоже тратится некоторое время).
Материалы по теме
- Realtime Procedural Terrain Generation (PDF, 1,52 Мб). Очень подробный и интересный материал по созданию ландшафтов — как с помощью диаграммы Вороного, так и алгоритмом diamond-square, с описанием способов эрозии и множеством иллюстраций и формул.
- Polygonal Map Generation, замечательная статья о построении ландшафта на основе диаграммы Вороного. Хорошо проиллюстрировано, имеется демонстрационный swf-файлик, множество ссылок на другие материалы.
- Fast Hydraulic Erosion Simulation and Visualization on GPU. Статья про оптимизацию симуляции водной эрозии, в наличии не только PDF и изображения, но и несколько видеороликов, помогающих понять, о чем речь. Безотносительно идеи оптимизировать процесс, переложив нагрузку на GPU, — в документе достаточно информации об механизмах эрозии.
- Несколько коротких статей о фрактальных алгоритмах: Generating Random Fractal Terrain, Fractal landscape, Fractal Terrains, Diamond-square algorithm.
 Распределение
Распределение