Дорогие друзья, доброго времени суток!
Уже не один раз здесь обсуждалась такая разновидность оптимизационных алгоритмов, как генетические алгоритмы. Однако, существуют и другие способы поиска оптимального решения в задачах с многими степенями свободы. Один из них (и, надо сказать, один из наиболее эффективных) — метод имитации отжига, о котором здесь ещё не рассказывали. Я решил устранить эту несправедливость и как можно более простыми словами познакомить вас с этим замечательным алгоритмом, а заодно привести пример его использования для решения несложной задачки.
Я понимаю, почему генетические алгоритмы пользуются такой большой популярностью: они очень образны и, следовательно, доступны для понимания. В самом деле, несложно и крайне интересно представить решение некой задачи, как реальный биологический процесс развития популяции живых существ с определёнными свойствами. Между тем, алгоритм отжига также имеет свой прототип в реальном мире (это понятно и из самого названия). Правда, пришёл он не из биологии, а из физики. Процесс, имитируемый данным алгоритмом, похож на образование веществом кристаллической структуры с минимальной энергией во время охлаждения и затвердевания, когда при высоких температурах частицы хаотично движутся, постепенно замедляясь и застывая в местах с наименьшей энергией. Только в случае математической задачи роль частиц вещества выполняют параметры, а роль энергии — функция, характеризующая оптимальность набора этих параметров.
Для начала тем, кто забыл, напомню, что же за вид задач мы пытаемся решать такими экзотическими методами. Существует целый ряд задач, чьё точное решение крайне трудно найти в силу большого количества изменяемых параметров. В общем случае у нас есть функция F, чей минимум (максимум) нам нужно найти, и набор её параметров x1..xn, каждый из которых может независимо меняться в своих пределах. Параметры и, соответственно, функция могут изменяться как дискретно, так и непрерывно. Ясно, что у такой функции, скорее всего, будет сложная зависимость от входных данных, имеющая множество локальных минимумов, тогда как мы ищем минимум глобальный. Конечно, всегда остаётся вариант решить задачу полным перебором, но он работает только в дискретном случае и при крайне ограниченном наборе входов. Вот тут и начинают действовать оптимизационные алгоритмы.
Чтобы не быть сухим, сразу расскажу о задаче, которую я буду решать в рамках этой статьи. Представим себе клетчатую доску размером m на l. Сторона клетки равна единице. На доске нужно найти такую расстановку n точек, чтобы длина минимальной ломаной, соединяющей эти точки, была максимальной. Обычная минимаксная задача. Очевидно, что в данном случае функция F считает длину минимальной ломаной для определённой расстановки точек, а параметрами её являются x и y координаты точек, т.е. 2*n параметров.
Итак, есть функция, характеризующая систему, и множество координат, на котором эта функция задана. Прежде всего нужно задать начальное состояние системы. Для этого берётся просто любое случайное состояние. Далее на каждом k-ом шаге мы
Зачем же нужна такая сложная схема с вероятностями переходов из точки в точку? Почему нельзя просто передвигаться строго от большей энергии к меньшей? Всё дело в уже упоминавшихся локальных минимумах, в которых решение может просто застрять. Чтобы выбраться из них и найти минимум глобальный, необходимо время от времени повышать энергию системы. При этом общая тенденция к поиску наименьшей энергии сохраняется. В этом и состоит суть метода имитации отжига.
Теперь, когда общая схема алгоритма ясна, вернёмся к нашим баранам. Будем реализовывать задачу на java. Для начала опишем доску с точками на ней.
Доска:
Ну что ж, все приготовления выполнены. Теперь мы можем начинать реализовывать сам алгоритм.
Вернувшись к общей схеме, мы встретим там упоминание о двух распределениях, зависящих от координат и температуры. Их нужно каким-то образом определить. Кроме того, нам нужен закон, по которому будет изменяться температура от итерации к итерации. Выбрав эти три функции, мы составим конкретную схему метода отжига. Надо сказать, что существует несколько модификаций алгоритма, отличающихся друг от друга распределениями и законом изменения температур. Они имеют свои плюсы и минусы, такие как быстрота, гарантия нахождения глобального минимума, сложность исполнения.
Я выбрал для своей задачи модификацию под названием сверхбыстрый отжиг («Very Fast Annealing»). Для начала определим распределение вероятности принятия нового состояния.

или в коде:
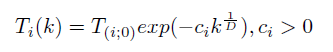
Где D — количество координат (т.е. 2*n), k — номер хода. Однако для простоты сделаем всё-таки общую температуру:
Наконец, распределение для новой координаты. Следующая величина характеризует относительное изменение одной координаты:
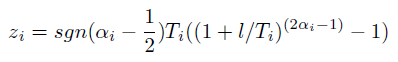
Где альфа — равномерно распределённая на отрезке [0, 1] величина. Если новая координата не укладывается в рамки своего изменения (в нашем случае — выходит за пределы доски), то расчёт производится снова.
Нужно отметить, что некоторые модификации метода имитации отжига дают статистическую гарантию нахождения оптимального решения. Это значит, что при верном выборе параметров алгоритм найдёт оптимальное решение за разумное время без перебора всех входов. Данная реализация находит ответ для доски 12x12 и 5 точек примерно за 15000 итераций. Напомню, что полное число вариантов расстановки равно 12^10. Очевидно, что трудности настройки параметров стоят такого выигрыша. Кстати, метод отжига по быстроте и точности по крайней мере не проигрывает генетическому алгоритму, а чаще всего опережает его.
Напоследок наглядный результат действия алгоритма.

Использованная литература:
А. Лопатин «Метод отжига»
Уже не один раз здесь обсуждалась такая разновидность оптимизационных алгоритмов, как генетические алгоритмы. Однако, существуют и другие способы поиска оптимального решения в задачах с многими степенями свободы. Один из них (и, надо сказать, один из наиболее эффективных) — метод имитации отжига, о котором здесь ещё не рассказывали. Я решил устранить эту несправедливость и как можно более простыми словами познакомить вас с этим замечательным алгоритмом, а заодно привести пример его использования для решения несложной задачки.
Я понимаю, почему генетические алгоритмы пользуются такой большой популярностью: они очень образны и, следовательно, доступны для понимания. В самом деле, несложно и крайне интересно представить решение некой задачи, как реальный биологический процесс развития популяции живых существ с определёнными свойствами. Между тем, алгоритм отжига также имеет свой прототип в реальном мире (это понятно и из самого названия). Правда, пришёл он не из биологии, а из физики. Процесс, имитируемый данным алгоритмом, похож на образование веществом кристаллической структуры с минимальной энергией во время охлаждения и затвердевания, когда при высоких температурах частицы хаотично движутся, постепенно замедляясь и застывая в местах с наименьшей энергией. Только в случае математической задачи роль частиц вещества выполняют параметры, а роль энергии — функция, характеризующая оптимальность набора этих параметров.
Для начала тем, кто забыл, напомню, что же за вид задач мы пытаемся решать такими экзотическими методами. Существует целый ряд задач, чьё точное решение крайне трудно найти в силу большого количества изменяемых параметров. В общем случае у нас есть функция F, чей минимум (максимум) нам нужно найти, и набор её параметров x1..xn, каждый из которых может независимо меняться в своих пределах. Параметры и, соответственно, функция могут изменяться как дискретно, так и непрерывно. Ясно, что у такой функции, скорее всего, будет сложная зависимость от входных данных, имеющая множество локальных минимумов, тогда как мы ищем минимум глобальный. Конечно, всегда остаётся вариант решить задачу полным перебором, но он работает только в дискретном случае и при крайне ограниченном наборе входов. Вот тут и начинают действовать оптимизационные алгоритмы.
Чтобы не быть сухим, сразу расскажу о задаче, которую я буду решать в рамках этой статьи. Представим себе клетчатую доску размером m на l. Сторона клетки равна единице. На доске нужно найти такую расстановку n точек, чтобы длина минимальной ломаной, соединяющей эти точки, была максимальной. Обычная минимаксная задача. Очевидно, что в данном случае функция F считает длину минимальной ломаной для определённой расстановки точек, а параметрами её являются x и y координаты точек, т.е. 2*n параметров.
Собственно, алгоритм
Итак, есть функция, характеризующая систему, и множество координат, на котором эта функция задана. Прежде всего нужно задать начальное состояние системы. Для этого берётся просто любое случайное состояние. Далее на каждом k-ом шаге мы
- сравниваем текущее значение F с наилучшим найденным; если текущее значение лучше — меняем глобальное наилучшее
- случайным образом генерируем новое состояние; распределение вероятности для него должно зависеть от текущего состояния и текущей температуры
- вычисляем значение функции для сгенерированной точки
- принимаем или не принимаем сгенерированное состояние в качестве текущего; вероятность этого решения должна зависеть от разности функций сгенерированного и текущего состояний и, конечно, от температуры (чем выше температура, тем больше вероятность принять состояние хуже текущего)
- если новое состояние не принято, генерируем другое и повторяем действия с третьего пункта, если принято — переходим к следующей итерации, понизив температуру (но чаще переход к следующему шагу производят в любом случае, чтобы избежать долгого зацикливания)
Зачем же нужна такая сложная схема с вероятностями переходов из точки в точку? Почему нельзя просто передвигаться строго от большей энергии к меньшей? Всё дело в уже упоминавшихся локальных минимумах, в которых решение может просто застрять. Чтобы выбраться из них и найти минимум глобальный, необходимо время от времени повышать энергию системы. При этом общая тенденция к поиску наименьшей энергии сохраняется. В этом и состоит суть метода имитации отжига.
И снова о точках на доске
Теперь, когда общая схема алгоритма ясна, вернёмся к нашим баранам. Будем реализовывать задачу на java. Для начала опишем доску с точками на ней.
Доска:
public class Board {
private Point[] points;
private int N;
private int width;
private int height;
public Board(int n, int w, int h) {
points = new Point[n];
N = n;
width = w;
height = h;
}
public Board(Board board) {
points = new Point[board.points.length];
for (int i = 0; i < points.length; i++)
points[i] = new Point(board.points[i].getX(), board.points[i].getY());
this.width = board.width;
this.height = board.height;
}
public int getPointsCount() {
return points.length;
}
public int getWidth() {
return width;
}
public int getHeight() {
return height;
}
public Point getPoint(int index) {
return points[index];
}
public void setPoint(int index, Point p) {
points[index] = p;
}
}
public class Point {
private int x;
private int y;
public Point(int x, int y) {
this.x = x;
this.y = y;
}
public double dist(Point p) {
return Math.sqrt((x - p.x) * (x - p.x) + (y - p.y) * (y - p.y));
}
public void move(int dx, int dy, int xBorder, int yBorder){
if(((x + dx) < xBorder) && ((x + dx) >= 0))
x += dx;
if(((y + dy) < yBorder) && ((y + dy) >= 0))
y += dy;
}
public int getX(){
return x;
}
public int getY(){
return y;
}
}
public class Polyline {
public Point p[];
public int N = 5;
public Polyline(int Num) {
N = Num;
p = new Point[N];
}
public double dist() {
double d = 0;
for (int i = 0; i < (N - 1); i++) {
d += p[i].dist(p[i + 1]);
}
return d;
}
}public class MinPolyline {
private double bestDist;
private Polyline bestMinPolyl;
private Board board;
public Polyline F(Board b) {
N = b.getPointsCount();
board = b;
int[] perm = new int[N];
boolean used[] = new boolean[N];
for (int i = 0; i < N; i++) {
perm[i] = i + 1;
used[i] = false;
}
bestDist = Double.MAX_VALUE;
permute (0, perm, used);
return bestMinPolyl;
}
void permute(int first_index, int[] perm, boolean[] used) {
if (first_index == N) {
Polyline polyl = new Polyline(N);
for (int i = 0; i < N; i++){
polyl.p[i] = board.getPoint(perm[i] - 1);
}
if (bestDist > polyl.dist()){
bestDist = polyl.dist();
bestMinPolyl = polyl;
}
return;
}
for (int i = 1; i < N+1; i++) {
if (used[i - 1]) continue;
perm[first_index] = i;
used[i - 1] = true;
permute(first_index + 1, perm, used);
used[i - 1] = false;
}
}
}Ну что ж, все приготовления выполнены. Теперь мы можем начинать реализовывать сам алгоритм.
Реализация алгоритма
Вернувшись к общей схеме, мы встретим там упоминание о двух распределениях, зависящих от координат и температуры. Их нужно каким-то образом определить. Кроме того, нам нужен закон, по которому будет изменяться температура от итерации к итерации. Выбрав эти три функции, мы составим конкретную схему метода отжига. Надо сказать, что существует несколько модификаций алгоритма, отличающихся друг от друга распределениями и законом изменения температур. Они имеют свои плюсы и минусы, такие как быстрота, гарантия нахождения глобального минимума, сложность исполнения.
Я выбрал для своей задачи модификацию под названием сверхбыстрый отжиг («Very Fast Annealing»). Для начала определим распределение вероятности принятия нового состояния.

или в коде:
h = 1 / (1 + Math.exp(-(minPolyl.F(board).dist()- maxDist) / T));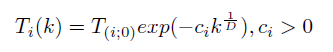
Где D — количество координат (т.е. 2*n), k — номер хода. Однако для простоты сделаем всё-таки общую температуру:
T = To * Math.exp(-decrement * Math.pow(i, (double)(1) / (2*(double)N)));Наконец, распределение для новой координаты. Следующая величина характеризует относительное изменение одной координаты:
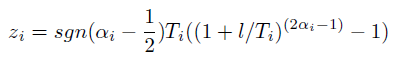
Где альфа — равномерно распределённая на отрезке [0, 1] величина. Если новая координата не укладывается в рамки своего изменения (в нашем случае — выходит за пределы доски), то расчёт производится снова.
z = (Math.pow((1 + 1/T), (2 * alpha - 1)) - 1) * T;
x = board.getPoint(moveNum).getX() + (int)(z * border);public class AnnealingOptimizer {
public int N;
public int width;
public int height;
public AnnealingOptimizer(int n, int width, int height) {
N = n;
this.width = width;
this.height = height;
}
public Board optimize(double To, double Tend, double decrement){
Board board = new Board(N, width, height);
Board bestBoard = new Board(N, width, height);
Random r = new Random();
double maxDist = 0;
double T = To;
double h;
MinPolyline minPolyl = new MinPolyline();
for (int j = 0; j < N; ++j){
board.setPoint(j, new Point(r.nextInt(height), r.nextInt(width)));
bestBoard.setPoint(j, board.getPoint(j));
}
int i = 1;
while (T > Tend){
for (int moveNum = 0; moveNum < board.getPointsCount(); ++moveNum){
NewX(board, moveNum, T, width, true);
NewX(board, moveNum, T, height, false);
}
if (minPolyl.F(board).dist() > maxDist){
bestBoard = new Board(board);
}else{
h = 1 / (1 + Math.exp(-(minPolyl.F(board).dist()- maxDist) / T));
if (r.nextDouble() > h){
board = new Board(bestBoard);
}else{
bestBoard = new Board(board);
}
}
maxDist = minPolyl.F(board).dist();
T = To * Math.exp(-decrement * Math.pow(i, (double)(1) / (2*(double)N)));
++i;
}
return bestBoard;
}
private void NewX (Board board, int moveNum, double T, int border, boolean xCoord) {
Random r = new Random();
int x;
double z;
double alpha = r.nextDouble();
z = (Math.pow((1 + 1/T), (2 * alpha - 1)) - 1) * T;
if (xCoord){
x = board.getPoint(moveNum).getX() + (int)(z * border);
if ((x < border) && (x >= 0)) {
board.getPoint(moveNum).move((int)(z * border), 0, width, height);
} else {
NewX(board, moveNum, T, border, xCoord);
}
} else {
x = board.getPoint(moveNum).getY() + (int)(z * border);
if ((x < border) && (x >= 0)) {
board.getPoint(moveNum).move(0, (int)(z * border), width, height);
} else {
NewX(board, moveNum, T, border, xCoord);
}
}
}
}Нужно отметить, что некоторые модификации метода имитации отжига дают статистическую гарантию нахождения оптимального решения. Это значит, что при верном выборе параметров алгоритм найдёт оптимальное решение за разумное время без перебора всех входов. Данная реализация находит ответ для доски 12x12 и 5 точек примерно за 15000 итераций. Напомню, что полное число вариантов расстановки равно 12^10. Очевидно, что трудности настройки параметров стоят такого выигрыша. Кстати, метод отжига по быстроте и точности по крайней мере не проигрывает генетическому алгоритму, а чаще всего опережает его.
Напоследок наглядный результат действия алгоритма.
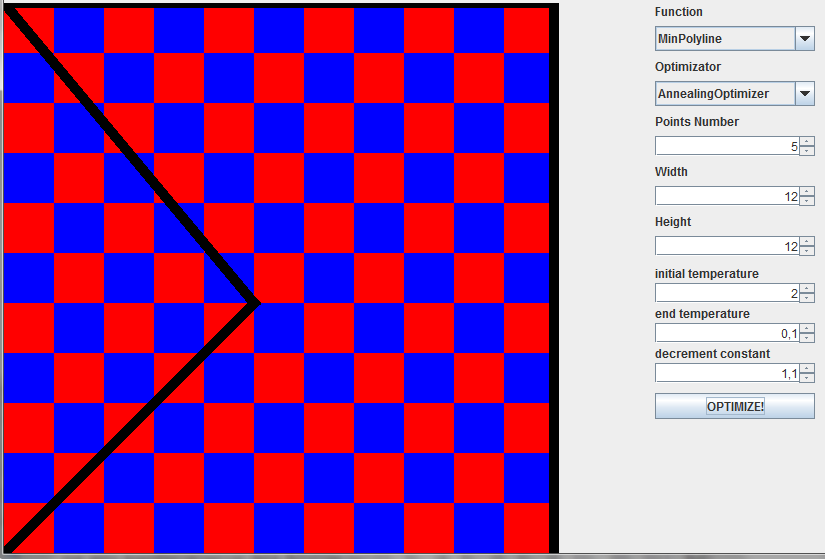
Использованная литература:
А. Лопатин «Метод отжига»