На самом деле никому не открою ничего нового, но то что находил, было с хитрой математикой (точнее не такой уж хитрой, но все равно лично для меня сложноватой для восприятия), а тут вроде получился простой свой велосипед.
И так что у нас уже есть:
Поиск на обычной прямоугольной сетке.
Что нам надо:
Поиск по гексагональной сетке с минимальными усилиями.
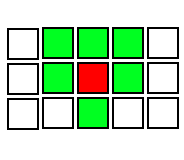
Первая же идея просто через столбец все сместить:
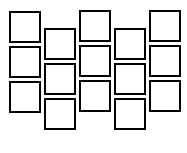
Тогда соседи текущей клетки выглядят примерно так:
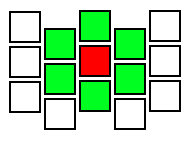
Как видно, связи между клетками по идее должны образовывать как раз гекс:

Но сразу же закрадывается подозрения, что тут должны быть совсем не квадраты, а прямоугольники:

Как не трудно посчитать k на рисунке будет равно sqrt(3)/2
В результате получаем сетку

Где размеры каждой клетки соотвествено w=sqrt(3)/2, h= 1, при это каждый нечетный столбец(если начинать отсчет с 0) смещен на 0,5
Дальше все идет проще, чтобы перевести координаты в номер клетки с поправкой на четный/нечетный столбец:
Чтобы наоборот, клетку поля перевести в координаты:
Теперь нам надо получить всех соседей выбранной клетки.
Они будут выглядеть примерно так, для четных столбцов(и симметрично для нечетных).

Теперь для полноценной реализации не хватает только способа нахождения расстояния между двумя клетками, можно конечно использовать банально Евклида, но это не наш вариант. За базовую основу возьмем диагональное расстояние на обычной сетке:
У нас ситуация ситуация похожая(тоже есть диагональные ходы), только чтобы сместится по вертикали(рассматривая ориентацию сетки как в примере), можно либо сделать один шаг по вертикали, либо 2 по горизонтали.
Но и тут есть маленькая деталь, если расстояние измеряется между двумя клетками из разных столбцов, то там будет еще не учтенное смещение в пол клетки. Поэтому yd надо определять чуть иначе:
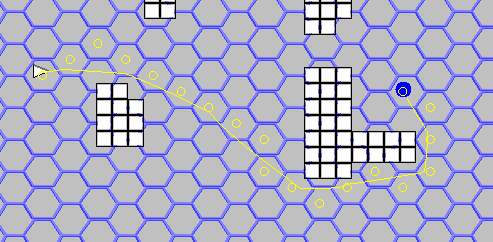
Теперь осталось натравить A* на это все, например как я это сделал тут, и тадам:

Конечно же существуют более красивые математические способы манипулирования гексагональной сеткой, но данный способ получился по моему мнению достаточно простым, чтобы иметь право на жизнь(и плюс в тесте производительности показал вполне хорошие результаты).
И так что у нас уже есть:
Поиск на обычной прямоугольной сетке.
Что нам надо:
Поиск по гексагональной сетке с минимальными усилиями.
Общая структура сетки
Первая же идея просто через столбец все сместить:
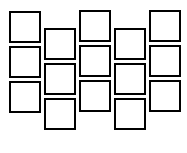
Тогда соседи текущей клетки выглядят примерно так:
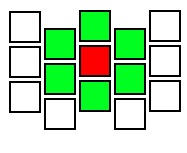
Как видно, связи между клетками по идее должны образовывать как раз гекс:
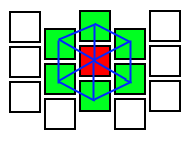
Но сразу же закрадывается подозрения, что тут должны быть совсем не квадраты, а прямоугольники:
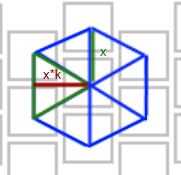
Как не трудно посчитать k на рисунке будет равно sqrt(3)/2
В результате получаем сетку
Где размеры каждой клетки соотвествено w=sqrt(3)/2, h= 1, при это каждый нечетный столбец(если начинать отсчет с 0) смещен на 0,5
Трансформация координат
Дальше все идет проще, чтобы перевести координаты в номер клетки с поправкой на четный/нечетный столбец:
(x,y)=>(x/w, (y-(x/w)%2)/h)Чтобы наоборот, клетку поля перевести в координаты:
(i,k)=>(i*w, k*h+h/2*(i%2))Соседи
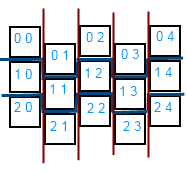
Теперь нам надо получить всех соседей выбранной клетки.
Они будут выглядеть примерно так, для четных столбцов(и симметрично для нечетных).
(i,k)=>(
(i+1,k),
(i-1,k),
(i,k+1),
(I,k-1),
(i+1,k+(1-2*i%2)),
(i-1,k+(1-2*i%2)))
Расстояние между двумя клетками
Теперь для полноценной реализации не хватает только способа нахождения расстояния между двумя клетками, можно конечно использовать банально Евклида, но это не наш вариант. За базовую основу возьмем диагональное расстояние на обычной сетке:
xd = abs(p1.X - p2.X);
yd = abs(p1.Y - p2.Y);
diagonal = min(xd, yd);
straight = xd + yd;
result = sqrt(2) * diagonal + (straight - (2 * diagonal)));
У нас ситуация ситуация похожая(тоже есть диагональные ходы), только чтобы сместится по вертикали(рассматривая ориентацию сетки как в примере), можно либо сделать один шаг по вертикали, либо 2 по горизонтали.
//если хватает горизонтального расстояния
if (xd >= yd * 2)
{
result = xd;
}
//если всеже придется идти строго вверх
else
{
result = xd + (yd – xd/2);
}
Но и тут есть маленькая деталь, если расстояние измеряется между двумя клетками из разных столбцов, то там будет еще не учтенное смещение в пол клетки. Поэтому yd надо определять чуть иначе:
yd =abs((p1.Y + (p1.X%2)/2) – (p2.Y + (p2.X%2)/2));Теперь осталось натравить A* на это все, например как я это сделал тут, и тадам:
Вместо послесловия
Конечно же существуют более красивые математические способы манипулирования гексагональной сеткой, но данный способ получился по моему мнению достаточно простым, чтобы иметь право на жизнь(и плюс в тесте производительности показал вполне хорошие результаты).