Сегментация изображения
Одной из основных задач обработки и анализа изображений является сегментация, т.е. разделение изображения на области, для которых выполняется определенный критерий однородности, например, выделение на изображении областей приблизительно одинаковой яркости. Понятие области изображения используется для определения связной группы элементов изображения, имеющих определенный общий признак (свойство).
Один из основных и простых способов — это построение сегментации с помощью порога. Порог — это признак (свойство), которое помогает разделить искомый сигнал на классы. Операция порогового разделения заключается в сопоставлении значения яркости каждого пикселя изображения с заданным значением порога.

Бинаризация
Операция порогового разделения, которая в результате дает бинарное изображение, называется бинаризацией. Целью операции бинаризации является радикальное уменьшение количества информации, содержащейся на изображении. В процессе бинаризации исходное полутоновое изображение, имеющее некое количество уровней яркости, преобразуется в черно-белое изображение, пиксели которого имеют только два значения – 0 и 1
Пороговая обработка изображения может проводиться разными способами.
Бинаризация с нижним порогом
Бинаризация с нижним порогом
Бинаризация с нижним порогом является наиболее простой операцией, в которой используется только одно значение порога:

Все значения вместо критерия становятся 1, в данном случае 255 (белый) и все значения(амплитуды) пикселей, которые больше порога t — 0 (черный).
Бинаризации с верхним порогом
Иногда можно использовать вариант первого метода, который дает негатив изображения, полученного в процессе бинаризации. Операция бинаризации с верхним порогом:
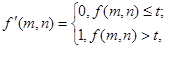
Бинаризация с двойным ограничением
Для выделения областей, в которых значения яркости пикселей может меняться в известном диапазоне, вводится бинаризация с двойным ограничением (t1<t2):
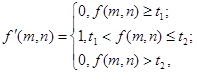
Так же возможны другие вариации с порогами, где пропускается только часть данных (средне полосовой фильтр).
Неполная пороговая обработка
Данное преобразование дает изображение, которое может быть проще для дальнейшего анализа, поскольку оно становится лишенным фона со всеми деталями, присутствующими на исходном изображении.

Многоуровневое пороговое преобразование
Данная операция формирует изображение, не являющееся бинарным, но состоящее из сегментов с различной яркостью.
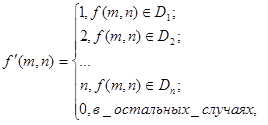
Что касается бинаризации, то по сути все. Хотя можно добавить, что есть глобальная, которая используется для всего изображения и так же существует локальная, которая захватывает часть картинки (изображения).
Локальная пороговая обработка
Метод Отса
Метод использует гистограмму распределения значений яркости пикселей растрового изображения. Строится гистограмма по значениям pi=ni/N, где N – это общее кол-во пикселей на изображении, ni – это кол-во пикселей с уровнем яркости i. Диапазон яркостей делится на два класса с помощью порогового значения уровня яркости k,k — целое значение от 0 до L. Каждому классу соответствуют относительные частоты ω0ω1:

Средние уровни для каждого из двух классов изображения:
Далее вычисляется максимальное значение оценки качества разделения изображения на две части:
где (σкл)2=ω0ω1(μ1-μ0)2, – межклассовая дисперсия, а (σобщ)2 – это общая дисперсия для всего изображения целиком.

Определение порога на основе градиента яркости изображения
Предположим, что анализируемое изображение можно разделить на два класса – объекты и фон. Алгоритм вычисления порогового значения состоит из следующих 2 шагов:
1. Определяется модуль градиента яркости для каждого пикселя
изображения
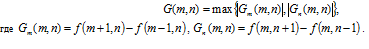
2. Вычисление порога:

Метод использования энтропии гистограммы
Метод приобрел свои различные формы описания и возможные вариации. Распределения общей массы порогов на определенное количество с использованием различных законов и форм распределения.
Глобальная пороговая обработка
Метод Бернсена
1. Обычная квадратная апертура с нечетным числом пикселей пробегает в цикле по всем пикселям исходного изображения. На каждом шаге находится Min и Max.
2. Находится среднее значение Avg= (Min + Max) /2.
3. Если текущий пиксель больше Avg<E — он становится белым, иначе — чёрным. E — некая константа заданная пользователем.
4. Если среднее меньше порога контраста — то текущий пиксель становится того цвета, который задавался параметром «цвет сомнительного пикселя».
Имеет ряд недостатков: после обработки монотонных областей яркости формируются сильные паразитные помехи, в некоторых случаях приводит к появлению ложных черных пятен
Метод Эйквила
Одним из самых производительных методов является метод Эйквеля. Его часто применяют для обработки четких и контрастных изображений. Согласно данному методу изображение обрабатывается с помощью двух концентрических окон: маленького – S, и большого L. Обычно форма окон принимается квадратной. Оба окна последовательно слева направо сверху вниз накладываются на изображение с шагом равным стороне маленького окна S. Для окна L рассчитывается порог B так, чтобы поделить пиксели на два кластера. Если математические ожидания уровня яркости в двух кластерах имеют разницу, превышающую некоторый заданный пользователем уровень /μ1-μ2/≥l, то все пиксели внутри окна S бинаризуются в соответствии с порогом T. В противном случае, яркость пикселей из окна S заменяется некоторым близким значением.
Метод Ниблэка
Идея данного метода состоит в варьировании порога яркости B бинаризации от точки к точке на основании локального значения стандартного отклонения. Порог яркости в точке (x, y) рассчитывается так:
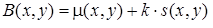
где μ(x, y) – среднее и s(x, y) — среднеквадратичное отклонение выборки для некоторой окрестности точки. Размер окрестности должен быть минимальным, но таким, чтобы сохранить локальные детали изображения. В то же время размер должен быть достаточно большим, чтобы понизить влияние шума на результат. Значение k определяет, какую часть границы объекта взять в качестве самого объекта. Значение k=-0.2 задает достаточно хорошее разделение объектов, если они представлены черным цветом, а значение k=+0.2, – если объекты представлены белым цветом.
Метод Яновица и Брукштейна
В качестве пороговой поверхности бинаризации используется поверхность потенциалов, строящаяся на основе локальной максимизации градиента яркости. начение градиента яркости часто рассчитывается с помощью контурного оператора Собеля или Кэнни. Изображение фильтруется с целью получения контурных линий толщины в 1 пиксель, а затем усредняющим фильтром 3×3. Потенциальная поверхность, теперь, строится по итерационной интерполирующей схеме. Расчет поверхности идет в порядке, начиная от контурных пикселей. Для каждого не контурного пикселя рассчитывается интерполяционный остаток R(x, y) и новое значение пикселя P(x, y) на n+1-ом шаге должно рассчитываться в соответствии с формулами:
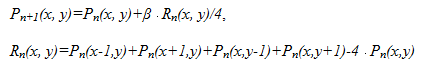
β в пределах 1≤β≤2 для быстрой сходимости.
Итого
Что нашел с радостью выложил вам, в дальнейшем, если получится и будет время, постараюсь реализовать часть алгоритмов. Это лишь малая часть всего, что сегодня существует, но я рад поделится и этим.
Спасибо за внимание.