На днях нужно было написать программу, вычисляющую среднеквадратичное приближение функции, заданной таблично, по степенному базису — методом наименьших квадратов. Сразу оговорюсь, что тригонометрический базис я не рассматривал и в этой статье его брать не буду. В конце статьи можно найти исходник программы на C#.
Пусть значения приближаемой функции f(x) заданы в N+1 узлах f(x0), ..., f(xN). Аппроксимирующую функцию будем выбирать из некоторого параметрического семейства F(x, c), где c = (c0, ..., cn)T — вектор параметров, N > n.
Принципиальным отличием задачи среднеквадратичного приближения от задачи интерполяции является то, что число узлов превышает число параметров. В данном случае практически всегда не найдется такого вектора параметров, для которого значения аппроксимирующей функции совпадали бы со значениями аппроксимируемой функции во всех узлах.
В этом случае задача аппроксимации ставится как задача поиска такого вектора параметров c = (c0, ..., cn)T, при котором значения аппроксимирующей функции как можно меньше отклонялись бы от значений аппроксимируемой функции F(x, c) в совокупности всех узлов.
Графически задачу можно представить так
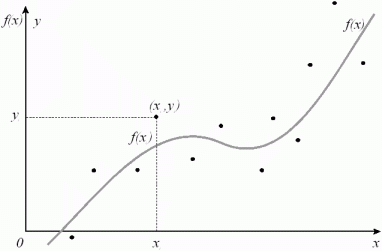
Запишем критерий среднеквадратичного приближения для метода наименьших квадратов:
J( c) = √ (Σi=0N[f(xi) — F(x, c) ]2) →min
Подкоренное выражение представляет собой квадратичную функцию относительно коэффициентов аппроксимирующего многочлена. Она непрерывна и дифференцируема по c0, ..., cn. Очевидно, что ее минимум находится в точке, где все частные производные равны нулю. Приравнивая к нулю частные производные, получим систему линейных алгебраических уравнений относительно неизвестных (искомых) коэффициентов многочлена наилучшего приближения.
Метод наименьших квадратов может быть применен для различных параметрических функций, но часто в инженерной практике в качестве аппроксимирующей функции используются многочлены по какому-либо линейно независимому базису {φk(x), k=0,...,n}:
F(x, c) = Σk=0n[ckφk(x)].
В этом случае система линейных алгебраических уравнений для определения коэффициентов будет иметь вполне определенный вид:
a00c0 + a01c1 +… + a0ncn = b0
a10c0 + a11c1 +… + a1ncn = b1
…
an0c0 + an1c1 +… + anncn = bn
akj = Σi=0N [φk(xi)φj(xi) ], bj = Σi=0N[f(xi)φj(xi) ]
Чтобы эта система имела единственное решение необходимо и достаточно, чтобы определитель матрицы А (определитель Грама) был отличен от нуля. Для того, чтобы система имела единственное решение необходимо и достаточно чтобы система базисных функций φk(x), k=0,...,n была линейно независимой на множестве узлов аппроксимации.
В этой статье рассматривается среднеквадратичное приближение многочленами по степенному базису {φk(x) = xk, k=0,...,n}.
А теперь перейдем к примеру. Требуется вывести эмпирическую формулу для приведенной табличной зависимости f(х), используя метод наименьших квадратов.
Примем в качестве аппроксимирующей функцию
y = F(x) = c0 + c1x + c2x2, то есть, n=2, N=4
Система уравнений для определения коэффициентов:
a00c0 + a01c1 +… + a0ncn = b0
a10c0 + a11c1 +… + a1ncn = b1
…
an0c0 + an1c1 +… + anncn = bn
akj = Σi=0N[φk(xi)φj(xi) ], bj = Σi=0N[f(xi)φj(xi) ]
Коэффициенты вычисляются по формулам:
a00 = N + 1 = 5, a01 = Σi=0Nxi = 11,25, a02 = Σi=0Nxi2 = 30,94
a10 = Σi=0Nxi = 11,25, a11 = Σi=0Nxi2 = 30,94, a12 = Σi=0Nxi3 = 94,92
a20 = Σi=0Nxi2 = 30,94, a21 = Σi=0Nxi3 = 94,92, a22 = Σi=0Nxi4 = 303,76
b0 = Σi=0Nyi = 11,25, b1 = Σi=0Nxiyi = 29, b2 = Σi=0Nxi2yi = 90,21
Решаем систему уравнений и получаем такие значения коэффициентов:
c0 = 4,822, c1 = -3,882, c2 = 0,999
Таким образом
y = 4,8 — 3,9x + x2
График получившейся функции
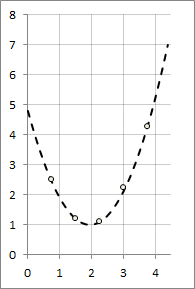
А теперь перейдем к тому, как написать код, который бы строил такую матрицу. А тут, оказывается, все совсем просто:
На входе функция получает таблицу значений функций — матрицу, в первом столбце которой содержатся значения x, во втором, соответственно, y, а также значение степенного базиса.
Сначала выделяется память под матрицу, в которую будут записаны коэффициенты для решения системы линейных уравнений. Затем, собственно, составляем матрицу — в sumA записываются значения коэффициентов aij, в sumB — bi, все по формуле, указанной выше в теоретической части.
Для решения составленной системы линейных алгебраических уравнений в моей программе используется метод Гаусса. Архив с проектом можно скачать по ссылке.
Скриншот работы программы на примере, решенном выше:

Используемые источники:
Сулимова В.В. Методические указания по курсу «Вычислительный практикум» — Тула, ТулГУ, 2009 — 65 с.
Теория
Пусть значения приближаемой функции f(x) заданы в N+1 узлах f(x0), ..., f(xN). Аппроксимирующую функцию будем выбирать из некоторого параметрического семейства F(x, c), где c = (c0, ..., cn)T — вектор параметров, N > n.
Принципиальным отличием задачи среднеквадратичного приближения от задачи интерполяции является то, что число узлов превышает число параметров. В данном случае практически всегда не найдется такого вектора параметров, для которого значения аппроксимирующей функции совпадали бы со значениями аппроксимируемой функции во всех узлах.
В этом случае задача аппроксимации ставится как задача поиска такого вектора параметров c = (c0, ..., cn)T, при котором значения аппроксимирующей функции как можно меньше отклонялись бы от значений аппроксимируемой функции F(x, c) в совокупности всех узлов.
Графически задачу можно представить так

Запишем критерий среднеквадратичного приближения для метода наименьших квадратов:
J( c) = √ (Σi=0N[f(xi) — F(x, c) ]2) →min
Подкоренное выражение представляет собой квадратичную функцию относительно коэффициентов аппроксимирующего многочлена. Она непрерывна и дифференцируема по c0, ..., cn. Очевидно, что ее минимум находится в точке, где все частные производные равны нулю. Приравнивая к нулю частные производные, получим систему линейных алгебраических уравнений относительно неизвестных (искомых) коэффициентов многочлена наилучшего приближения.
Метод наименьших квадратов может быть применен для различных параметрических функций, но часто в инженерной практике в качестве аппроксимирующей функции используются многочлены по какому-либо линейно независимому базису {φk(x), k=0,...,n}:
F(x, c) = Σk=0n[ckφk(x)].
В этом случае система линейных алгебраических уравнений для определения коэффициентов будет иметь вполне определенный вид:
a00c0 + a01c1 +… + a0ncn = b0
a10c0 + a11c1 +… + a1ncn = b1
…
an0c0 + an1c1 +… + anncn = bn
akj = Σi=0N [φk(xi)φj(xi) ], bj = Σi=0N[f(xi)φj(xi) ]
Чтобы эта система имела единственное решение необходимо и достаточно, чтобы определитель матрицы А (определитель Грама) был отличен от нуля. Для того, чтобы система имела единственное решение необходимо и достаточно чтобы система базисных функций φk(x), k=0,...,n была линейно независимой на множестве узлов аппроксимации.
В этой статье рассматривается среднеквадратичное приближение многочленами по степенному базису {φk(x) = xk, k=0,...,n}.
Пример
А теперь перейдем к примеру. Требуется вывести эмпирическую формулу для приведенной табличной зависимости f(х), используя метод наименьших квадратов.
| x | 0,75 | 1,50 | 2,25 | 3,00 | 3,75 |
| y | 2,50 | 1,20 | 1,12 | 2,25 | 4,28 |
Примем в качестве аппроксимирующей функцию
y = F(x) = c0 + c1x + c2x2, то есть, n=2, N=4
Система уравнений для определения коэффициентов:
a00c0 + a01c1 +… + a0ncn = b0
a10c0 + a11c1 +… + a1ncn = b1
…
an0c0 + an1c1 +… + anncn = bn
akj = Σi=0N[φk(xi)φj(xi) ], bj = Σi=0N[f(xi)φj(xi) ]
Коэффициенты вычисляются по формулам:
a00 = N + 1 = 5, a01 = Σi=0Nxi = 11,25, a02 = Σi=0Nxi2 = 30,94
a10 = Σi=0Nxi = 11,25, a11 = Σi=0Nxi2 = 30,94, a12 = Σi=0Nxi3 = 94,92
a20 = Σi=0Nxi2 = 30,94, a21 = Σi=0Nxi3 = 94,92, a22 = Σi=0Nxi4 = 303,76
b0 = Σi=0Nyi = 11,25, b1 = Σi=0Nxiyi = 29, b2 = Σi=0Nxi2yi = 90,21
Решаем систему уравнений и получаем такие значения коэффициентов:
c0 = 4,822, c1 = -3,882, c2 = 0,999
Таким образом
y = 4,8 — 3,9x + x2
График получившейся функции
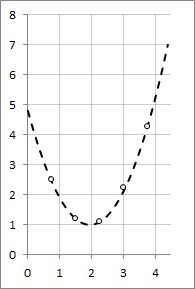
Релизация на C#
А теперь перейдем к тому, как написать код, который бы строил такую матрицу. А тут, оказывается, все совсем просто:
private double[,] MakeSystem(double[,] xyTable, int basis)
{
double[,] matrix = new double[basis, basis + 1];
for (int i = 0; i < basis; i++)
{
for (int j = 0; j < basis; j++)
{
matrix[i, j] = 0;
}
}
for (int i = 0; i < basis; i++)
{
for (int j = 0; j < basis; j++)
{
double sumA = 0, sumB = 0;
for (int k = 0; k < xyTable.Length / 2; k++)
{
sumA += Math.Pow(xyTable[0, k], i) * Math.Pow(xyTable[0, k], j);
sumB += xyTable[1, k] * Math.Pow(xyTable[0, k], i);
}
matrix[i, j] = sumA;
matrix[i, basis] = sumB;
}
}
return matrix;
}На входе функция получает таблицу значений функций — матрицу, в первом столбце которой содержатся значения x, во втором, соответственно, y, а также значение степенного базиса.
Сначала выделяется память под матрицу, в которую будут записаны коэффициенты для решения системы линейных уравнений. Затем, собственно, составляем матрицу — в sumA записываются значения коэффициентов aij, в sumB — bi, все по формуле, указанной выше в теоретической части.
Для решения составленной системы линейных алгебраических уравнений в моей программе используется метод Гаусса. Архив с проектом можно скачать по ссылке.
Скриншот работы программы на примере, решенном выше:
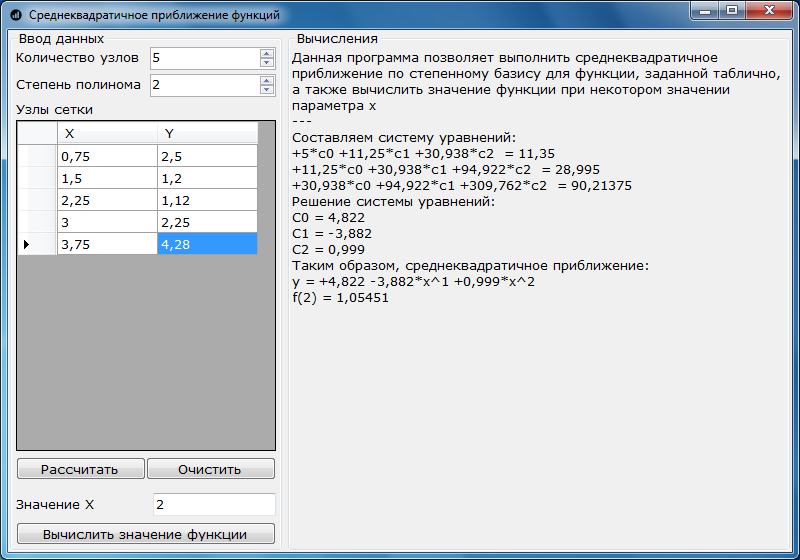
Используемые источники:
Сулимова В.В. Методические указания по курсу «Вычислительный практикум» — Тула, ТулГУ, 2009 — 65 с.