Фильтр Калмана — это, наверное, самый популярный алгоритм фильтрации, используемый во многих областях науки и техники. Благодаря своей простоте и эффективности его можно встретить в GPS-приемниках, обработчиках показаний датчиков, при реализации систем управления и т.д.
Про фильтр Калмана в интернете есть очень много статей и книг (в основном на английском), но у этих статей довольно большой порог вхождения, остается много туманных мест, хотя на самом деле это очень ясный и прозрачный алгоритм. Я попробую рассказать о нем простым языком, с постепенным нарастанием сложности.
Любой измерительный прибор обладает некоторой погрешностью, на него может оказывать влияние большое количество внешних и внутренних воздействий, что приводит к тому, что информация с него оказывается зашумленной. Чем сильнее зашумлены данные тем сложнее обрабатывать такую информацию.
Фильтр — это алгоритм обработки данных, который убирает шумы и лишнюю информацию. В фильтре Калмана есть возможность задать априорную информацию о характере системе, связи переменных и на основании этого строить более точную оценку, но даже в простейшем случае (без ввода априорной информации) он дает отличные результаты.
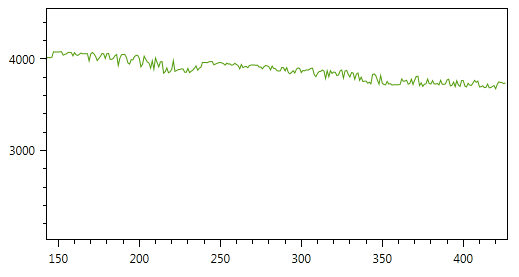
Рассмотрим простейший пример — предположим нам необходимо контролировать уровень топлива в баке. Для этого в бак устанавливается емкостный датчик, он очень прост в обслуживании, но обладает некоторыми недостатками — например, зависимость от заправляемого топлива (диэлектрическая проницаемость топлива зависит от многих факторов, например, от температуры), большое влияние «болтанки» в баке. В итоге, информация с него представляет типичную «пилу» с приличной амплитудой. Такого рода датчики часто устанавливаются на тяжелой карьерной технике (не смущайтесь объемам бака):

Немного отвлечемся и познакомимся с самим алгоритмом. Фильтр Калмана использует динамическую модель системы (например, физический закон движения), известные управляющие воздействия и множество последовательных измерений для формирования оптимальной оценки состояния. Алгоритм состоит из двух повторяющихся фаз: предсказание и корректировка. На первом рассчитывается предсказание состояния в следующий момент времени (с учетом неточности их измерения). На втором, новая информация с датчика корректирует предсказанное значение (также с учетом неточности и зашумленности этой информации):
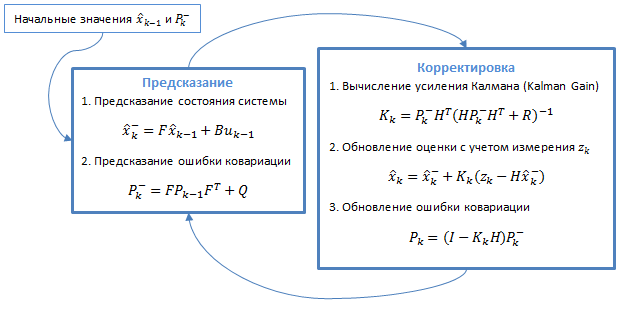
Уравнения представлены в матричной форме, если вы не знаете линейную алгебру — ничего страшного, дальше будет упрощенная версия без матриц для случая с одной переменной. В случае с одной переменной матрицы вырождаются в скалярные значения.
Разберемся сначала в обозначениях: подстрочный индекс обозначает момент времени: k — текущий, (k-1) — предыдущий, знак «минус» в верхнем индексе обозначает, что это предсказанное промежуточное значение.
Описание переменных представлены на следующих изображениях:

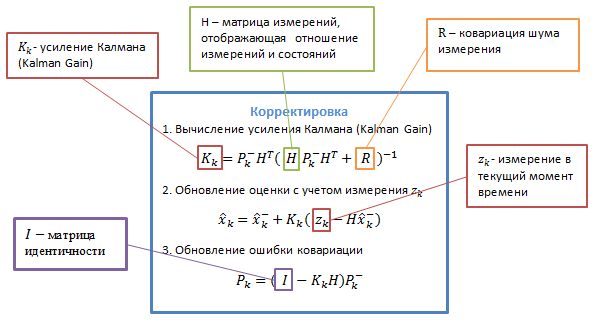
Можно долго и нудно описывать, что означают все эти таинственные матрицы переходов, но лучше, на мой взгляд, на реальном примере попробовать применить алгоритм — чтобы абстрактные значения обрели реальный смысл.
Вернемся к примеру с датчиком уровня топлива, так как состояние системы представлено одной переменной (объем топлива в баке), то матрицы вырождаются в обычные уравнения:

Для того, чтобы применить фильтр, необходимо определить матрицы/значения переменных определяющих динамику системы и измерений F, B и H:
F — переменная описывающая динамику системы, в случае с топливом — это может быть коэффициент определяющий расход топлива на холостых оборотах за время дискретизации (время между шагами алгоритма). Однако помимо расхода топлива, существуют ещё и заправки… поэтому для простоты примем эту переменную равную 1 (то есть мы указываем, что предсказываемое значение будет равно предыдущему состоянию).
B — переменная определяющая применение управляющего воздействия. Если бы у нас были дополнительная информация об оборотах двигателя или степени нажатия на педаль акселератора, то этот параметр бы определял как изменится расход топлива за время дискретизации. Так как управляющих воздействий в нашей модели нет (нет информации о них), то принимаем B = 0.
H — матрица определяющая отношение между измерениями и состоянием системы, пока без объяснений примем эту переменную также равную 1.
R — ошибка измерения может быть определена испытанием измерительных приборов и определением погрешности их измерения.
Q — определение шума процесса является более сложной задачей, так как требуется определить дисперсию процесса, что не всегда возможно. В любом случае, можно подобрать этот параметр для обеспечения требуемого уровня фильтрации.
Чтобы развеять оставшиеся непонятности реализуем упрощенный алгоритм на C# (без матриц и управляющего воздействия):
Результат фильтрации с данными параметрами представлен на рисунке (для настройки степени сглаживания — можно изменять параметры Q и R):
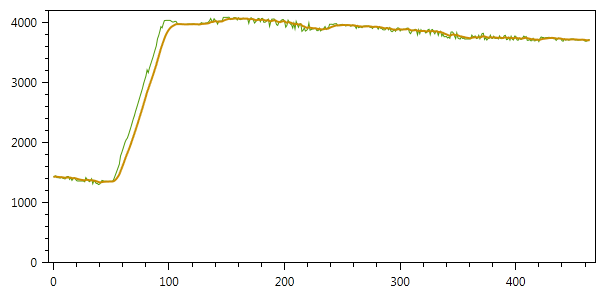
За рамками статьи осталось самое интересное — применение фильтра Калмана для нескольких переменных, задание взаимосвязи между ними и автоматический вывод значений для ненаблюдаемых переменных. Постараюсь продолжить тему как только появится время.
Надеюсь описание получилось не сильно утомительным и сложным, если остались вопросы и уточнения — добро пожаловать в комментарии )
UPD: Список источников:
CS373 — PROGRAMMING A ROBOTIC CAR — очень рекомендую
Википедия (русская)
Википедия (англ.)
На хабре: 1 и 2
Более серьезные источники:
Greg Welch, Gary Bishop, «An Introduction to the Kalman Filter», 2001
M.S.Grewal, A.P. Andrews, «Kalman Filtering — Theory and Practice Using MATLAB», Wiley, 2001
UPD2: приведенный в статье пример — чисто демонстрационный. Основное применение фильтра более сложные системы. Например, в случае определение координат автомобиля можно связать gps-координаты, угол поворота руля, обороты двигателя… и все это даст повышение точности координат.
Про фильтр Калмана в интернете есть очень много статей и книг (в основном на английском), но у этих статей довольно большой порог вхождения, остается много туманных мест, хотя на самом деле это очень ясный и прозрачный алгоритм. Я попробую рассказать о нем простым языком, с постепенным нарастанием сложности.
Для чего он нужен?
Любой измерительный прибор обладает некоторой погрешностью, на него может оказывать влияние большое количество внешних и внутренних воздействий, что приводит к тому, что информация с него оказывается зашумленной. Чем сильнее зашумлены данные тем сложнее обрабатывать такую информацию.
Фильтр — это алгоритм обработки данных, который убирает шумы и лишнюю информацию. В фильтре Калмана есть возможность задать априорную информацию о характере системе, связи переменных и на основании этого строить более точную оценку, но даже в простейшем случае (без ввода априорной информации) он дает отличные результаты.
Рассмотрим простейший пример — предположим нам необходимо контролировать уровень топлива в баке. Для этого в бак устанавливается емкостный датчик, он очень прост в обслуживании, но обладает некоторыми недостатками — например, зависимость от заправляемого топлива (диэлектрическая проницаемость топлива зависит от многих факторов, например, от температуры), большое влияние «болтанки» в баке. В итоге, информация с него представляет типичную «пилу» с приличной амплитудой. Такого рода датчики часто устанавливаются на тяжелой карьерной технике (не смущайтесь объемам бака):
Фильтр Калмана
Немного отвлечемся и познакомимся с самим алгоритмом. Фильтр Калмана использует динамическую модель системы (например, физический закон движения), известные управляющие воздействия и множество последовательных измерений для формирования оптимальной оценки состояния. Алгоритм состоит из двух повторяющихся фаз: предсказание и корректировка. На первом рассчитывается предсказание состояния в следующий момент времени (с учетом неточности их измерения). На втором, новая информация с датчика корректирует предсказанное значение (также с учетом неточности и зашумленности этой информации):

Уравнения представлены в матричной форме, если вы не знаете линейную алгебру — ничего страшного, дальше будет упрощенная версия без матриц для случая с одной переменной. В случае с одной переменной матрицы вырождаются в скалярные значения.
Разберемся сначала в обозначениях: подстрочный индекс обозначает момент времени: k — текущий, (k-1) — предыдущий, знак «минус» в верхнем индексе обозначает, что это предсказанное промежуточное значение.
Описание переменных представлены на следующих изображениях:
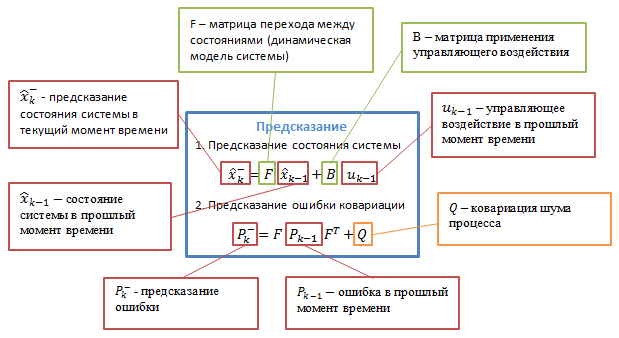
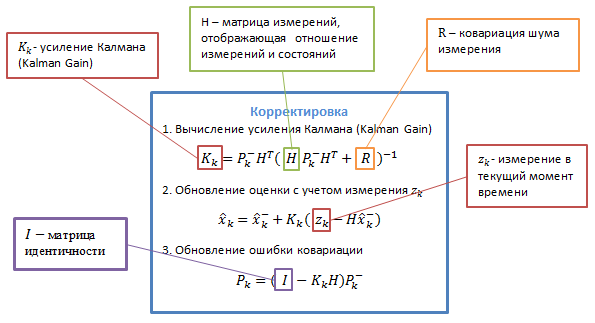
Можно долго и нудно описывать, что означают все эти таинственные матрицы переходов, но лучше, на мой взгляд, на реальном примере попробовать применить алгоритм — чтобы абстрактные значения обрели реальный смысл.
Опробуем в деле
Вернемся к примеру с датчиком уровня топлива, так как состояние системы представлено одной переменной (объем топлива в баке), то матрицы вырождаются в обычные уравнения:
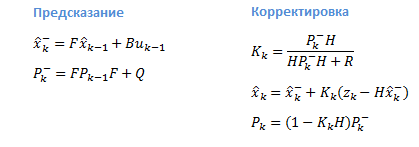
Определение модели процесса
Для того, чтобы применить фильтр, необходимо определить матрицы/значения переменных определяющих динамику системы и измерений F, B и H:
F — переменная описывающая динамику системы, в случае с топливом — это может быть коэффициент определяющий расход топлива на холостых оборотах за время дискретизации (время между шагами алгоритма). Однако помимо расхода топлива, существуют ещё и заправки… поэтому для простоты примем эту переменную равную 1 (то есть мы указываем, что предсказываемое значение будет равно предыдущему состоянию).
B — переменная определяющая применение управляющего воздействия. Если бы у нас были дополнительная информация об оборотах двигателя или степени нажатия на педаль акселератора, то этот параметр бы определял как изменится расход топлива за время дискретизации. Так как управляющих воздействий в нашей модели нет (нет информации о них), то принимаем B = 0.
H — матрица определяющая отношение между измерениями и состоянием системы, пока без объяснений примем эту переменную также равную 1.
Определение сглаживающих свойств
R — ошибка измерения может быть определена испытанием измерительных приборов и определением погрешности их измерения.
Q — определение шума процесса является более сложной задачей, так как требуется определить дисперсию процесса, что не всегда возможно. В любом случае, можно подобрать этот параметр для обеспечения требуемого уровня фильтрации.
Реализуем в коде
Чтобы развеять оставшиеся непонятности реализуем упрощенный алгоритм на C# (без матриц и управляющего воздействия):
class KalmanFilterSimple1D
{
public double X0 {get; private set;} // predicted state
public double P0 { get; private set; } // predicted covariance
public double F { get; private set; } // factor of real value to previous real value
public double Q { get; private set; } // measurement noise
public double H { get; private set; } // factor of measured value to real value
public double R { get; private set; } // environment noise
public double State { get; private set; }
public double Covariance { get; private set; }
public KalmanFilterSimple1D(double q, double r, double f = 1, double h = 1)
{
Q = q;
R = r;
F = f;
H = h;
}
public void SetState(double state, double covariance)
{
State = state;
Covariance = covariance;
}
public void Correct(double data)
{
//time update - prediction
X0 = F*State;
P0 = F*Covariance*F + Q;
//measurement update - correction
var K = H*P0/(H*P0*H + R);
State = X0 + K*(data - H*X0);
Covariance = (1 - K*H)*P0;
}
}
// Применение...
var fuelData = GetData();
var filtered = new List<double>();
var kalman = new KalmanFilterSimple1D(f: 1, h: 1, q: 2, r: 15); // задаем F, H, Q и R
kalman.SetState(fuelData[0], 0.1); // Задаем начальные значение State и Covariance
foreach(var d in fuelData)
{
kalman.Correct(d); // Применяем алгоритм
filtered.Add(kalman.State); // Сохраняем текущее состояние
}
Результат фильтрации с данными параметрами представлен на рисунке (для настройки степени сглаживания — можно изменять параметры Q и R):
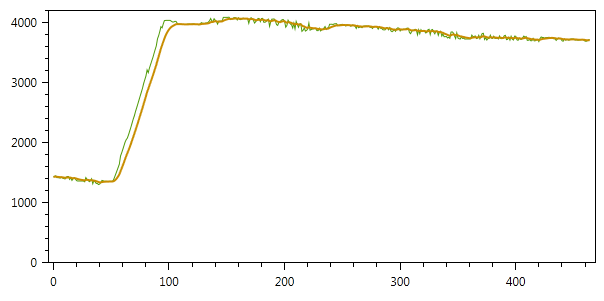
За рамками статьи осталось самое интересное — применение фильтра Калмана для нескольких переменных, задание взаимосвязи между ними и автоматический вывод значений для ненаблюдаемых переменных. Постараюсь продолжить тему как только появится время.
Надеюсь описание получилось не сильно утомительным и сложным, если остались вопросы и уточнения — добро пожаловать в комментарии )
UPD: Список источников:
CS373 — PROGRAMMING A ROBOTIC CAR — очень рекомендую
Википедия (русская)
Википедия (англ.)
На хабре: 1 и 2
Более серьезные источники:
Greg Welch, Gary Bishop, «An Introduction to the Kalman Filter», 2001
M.S.Grewal, A.P. Andrews, «Kalman Filtering — Theory and Practice Using MATLAB», Wiley, 2001
UPD2: приведенный в статье пример — чисто демонстрационный. Основное применение фильтра более сложные системы. Например, в случае определение координат автомобиля можно связать gps-координаты, угол поворота руля, обороты двигателя… и все это даст повышение точности координат.