Итак в статье Перцептрон Розенблатта — что забыто и придумано историей? в принципе как и ожидалось всплыло некоторая не осведомленность о сути перцептрона Розенблатта (у кого-то больше, у кого-то меньше). Но честно говоря я думал будет хуже. Поэтому для тех кто умеет и хочет слушать я обещал написать как так получается, что случайные связи в первом слое выполняют такую сложную задачу отображения не сепарабельного (линейно не разделимого) представления задачи в сепарабельное (линейно разделимое).
Честно говоря, я мог сослаться просто на теорему сходимости Розенблатта, но так как сам не люблю когда меня «посылают в гугл», то давайте разбираться. Но я исхожу из-то, что Вы знаете по подлинникам, что такое перцептрон Розенблатта (хотя проблемы в понимании всплыли, но я все же надеюсь что только у отдельных людей).
Начнем с матчасти
Итак, первое что нам нужно знать это, что такое А-матрица перцептрона и G-матрица перцептрона. Дам ссылки на википедию, писал сам поэтому доверять можно (прямо из оригинала):
1. А-матрица перцептрона
2. G-матрица перцептрона, тут надо обратить внимание на Связь А и G — матриц перцептрона
кто это не освоит, прошу дальше не читать, закройте статью и покурите — эта статья не для вас. Не спешите, не все сразу в жизни становится понятно, у меня тоже ушло на изучение нюансов перцептрона пару лет. Читать тут мало — делайте эксперименты.
Далее поговорим о теории сходимости перцептрона. О ней много говорят, но уверен 50% её в глаза не видели.
Итак, из одной моей научной статьи:
Доказательства я естественно рассматривать не буду (см. оригинал), но что нам далее будет важно — схождение перцептрона математически не гарантируется (не гарантируется не означает не будет — при простых входных данных будет, даже если нарушить, речь идет именно о произвольных входных данных) в двух случаях:
1. Если число примеров в обучающей выборке будет больше чем число нейронов в среднем слое (А-элементов)
2. Если у G матрицы детерминант равен нулю
По первой части, все просто, мы всегда можем выставить число А-элементов равным числу примеров в обучающей выборке.
А вот, вторая часть особенно интересна в свете нашего вопроса. Если вы справились с пониманием, что же это за G-матрица, то ясно, что как раз она зависит от входных данных и того какие связи образовались случайно в первом слое.
И теперь мы переходим к вопросу:
Вероятность активности А – элементов
Дальше я немного пропущу детали и дам сразу рисунок:
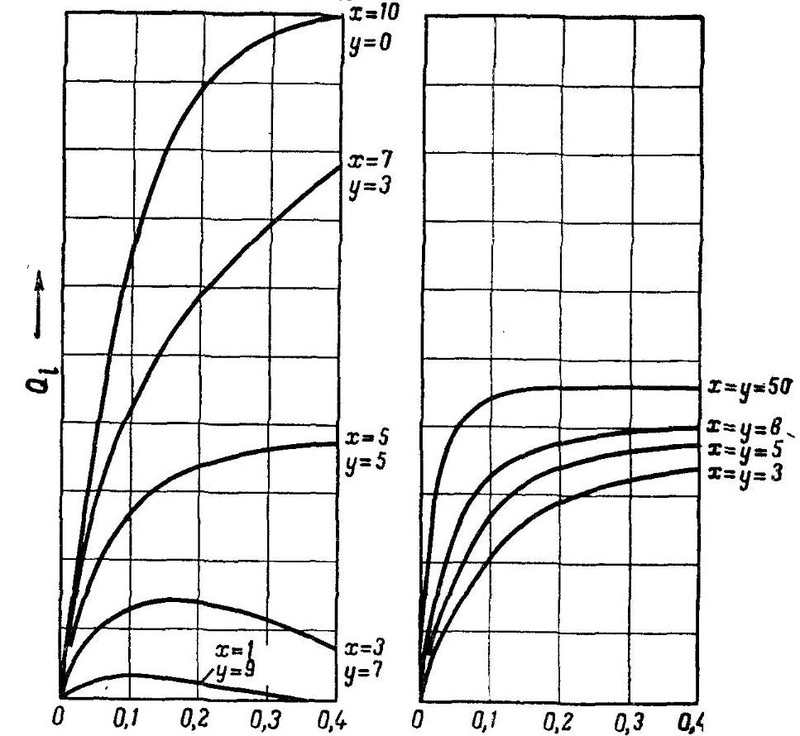
это т.н. Q-функции проанализированные Розенблаттом. В детали я вдаваться не буду, но тут важно, что:
x это число возбуждающих связей в первом слое, подходящие к одному А-элементу (вес +1) и y число тормозящих (вес -1). По оси y на рисунке показана величина этой Q-функции, которая зависит от относительного числа освещенных элементов на сетчатке (1 на входе).
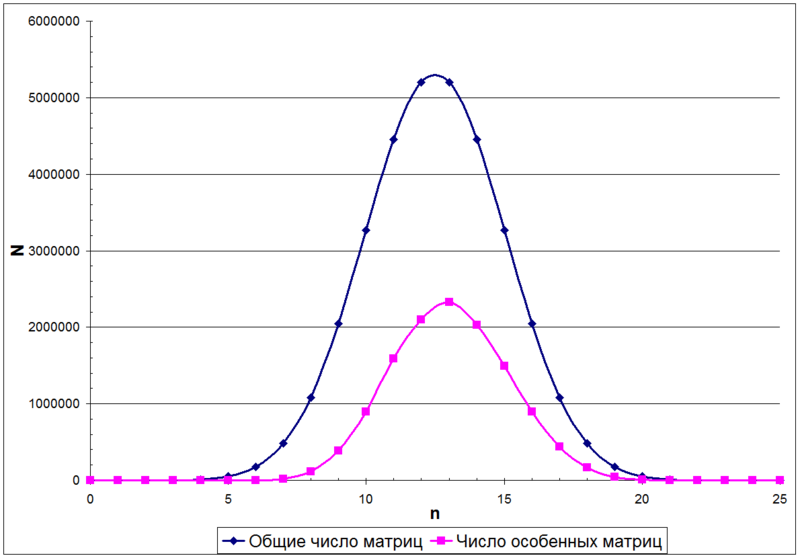
А этом случае число единиц в матрице А будет описываться биномиальным распределением. Для примера, на следующем рисунке показано распределение числа матриц N в зависимости от количества единиц n в матрице, размером 5х5
И наконец, какова вероятность того, что А матрица особенная?
И вот что получается видно на следующем рисунке (это вероятности появления не особенных матриц в зависимости от их размера):
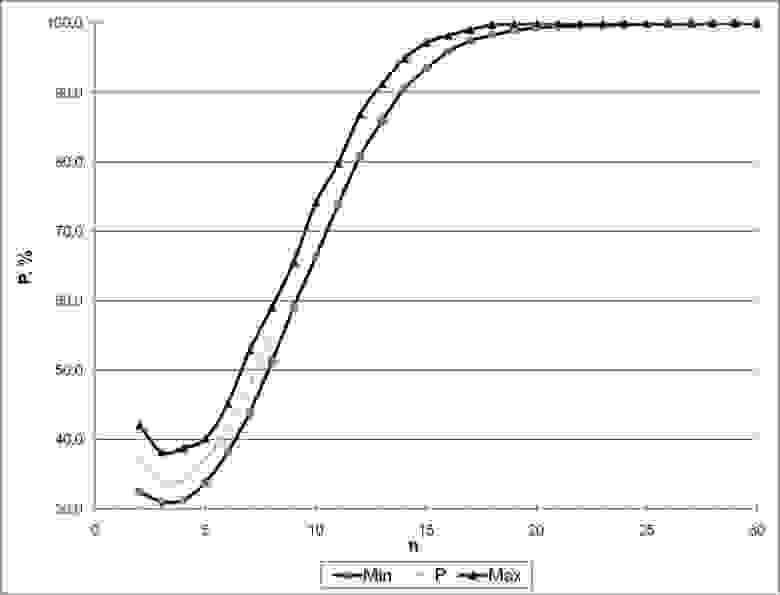
Итак, отсюда видно, что уже при размере матрицы 30 x 30 (т.е. когда число А-элементов 30 и больше) можно говорить почти о 100% уверенности, что случайно полученная матрица будет не особенная. Это и является тем окончательным практическим условием, при котором перцептрон Розенблатта будет формировать пространство, удовлетворяющее гипотезе компактности. Практически же надежнее иметь минимум порядка 100 А-элементов для исключения случая, когда G-матрица становится особенной.
И в заключение. А теперь задайтесь вопросом: а гарантирует ли MLP+BackProp, то о чем я вам здесь изложил в отношении перцептрона Розенблатта? Убедительных доказательств этому я нигде не нашел (только не кидайте ссылки на мат. доказательства сходимости градиентного спуска — это к этому не относится, лучше всего моим оппонентам советую написать свою вразумительную статью на этот счет: "на Хабрахабре приветствуются мысли из своей головы" — будет конструктивнее). Но исходя из наличия проблемы попадания в локальные минимумы при использовании BackProp — тут похоже не все чисто и гладко, как с перцептроном Розенблатта.
upd. что я несколько упустил из вида в изложении, и в ходе диалога мы тут уточнили. Спасибо retran и justserega за наводящие вопросы.
Резюме. В следствиях 1 и 2, говорится, что в определенных условиях решение невозможно. Тут я доказал, что такие условия при n > 30 не наступают (Розенблатт этим не занимался). Но у читателей возникло два вопроса
1. Хорошо А-матрица (а через неё и G) пригодна с высокой вероятностью. Но как это помогает перейти в другое пространство?. Действительно, не очень очевидно. Поясняю. А-матрица это и есть «другое пространство» — пространство признаков. Факт того, что матрица не является особенной и эта матрица на одну размерность больше чем исходная — и есть признак того, что она может быть разделена линейно. (это следует из следствий и теоремы 3)
2. "есть ли доказательства, что алгоритм коррекции ошибки в перцептроне Розенблатта сойдется?". Действительно, теорема №3 говорит только о том, что решение существует. Это уже означает, что это решение существует в пространстве признаков, т.е. после работы случайного первого слоя. Алгоритм же коррекции ошибки обучает второй слой, и существует у Розенблатта теорема №4, в которой он доказывает, что существующие возможные решения (теорема 3, что они вообще есть) могут быть достигнуты именно при применении алгоритма обучения с коррекцией ошибки.
Еще важный момент следует из того, что А-матрица зависит с одной стороны от входных данных, а с другой от случайной матрицы связей. Точнее происходит отображение входной матрицы в матрицу А через случайный оператор (образованные случайно связи ). Если ввести меру случайности, как скорость появления подпоследовательностей которые будут повторяться (псевдослучайность), то окажется: (1) если это совсем не случайная, а построенный по некоторым правилам оператор (т.е. соединения первого слоя), то существенно возрастает вероятность получить А-матрицу особенной (2) если же после умножения входной матрицы на полученную нами псевдослучайность А-матрица имеет не регулярный, а хаотический разброс единиц (назовем это условие R) — то это как раз то, что выше мы в статье анализировали.
Здесь я вам открою мною опробованную вещь. По идеи биномиальной модели случайности при создании связей (это когда берется А-элемент и от него случайно проводятся N возбуждающих и M тормозяцих связей к S-элементам) достаточно, чтобы выполнить условие R. Но чтобы ускорить процесс схождения, можно получить больший уровень хаоса в матрице А. Как это сделать — нам как раз расказывает криптография. Вот такая связь с криптографией тут еще нарисовалась.
Честно говоря, я мог сослаться просто на теорему сходимости Розенблатта, но так как сам не люблю когда меня «посылают в гугл», то давайте разбираться. Но я исхожу из-то, что Вы знаете по подлинникам, что такое перцептрон Розенблатта (хотя проблемы в понимании всплыли, но я все же надеюсь что только у отдельных людей).
Начнем с матчасти
Итак, первое что нам нужно знать это, что такое А-матрица перцептрона и G-матрица перцептрона. Дам ссылки на википедию, писал сам поэтому доверять можно (прямо из оригинала):
1. А-матрица перцептрона
2. G-матрица перцептрона, тут надо обратить внимание на Связь А и G — матриц перцептрона
кто это не освоит, прошу дальше не читать, закройте статью и покурите — эта статья не для вас. Не спешите, не все сразу в жизни становится понятно, у меня тоже ушло на изучение нюансов перцептрона пару лет. Читать тут мало — делайте эксперименты.
Далее поговорим о теории сходимости перцептрона. О ней много говорят, но уверен 50% её в глаза не видели.
Итак, из одной моей научной статьи:
Была доказана следующая теорема:
«''Теорема 3.'' Даны элементарный перцептрон, пространство стимулов W и какая-то классификация C(W). Тогда для существования решения необходимо и достаточно, чтобы существовал некоторый вектор u, лежащий в том же ортанте, что и C(W), и некоторый вектор x, такой, что Gx=u .»
а также два прямых следствия из этой теоремы:
«''Следствие 1.'' Даны элементарный перцептрон и пространство стимулов W. Тогда, если G — особенная матрица (детерминант которой равен нулю), то имеется некоторая классификация C(W), для которой решения не существует.»
«''Следствие 2.'' Если число стимулов в пространстве W больше числа А – элементов элементарного перцептрона, то существует некоторая классификация C(W), для которой решения не существует».
Пространством стимулов Розенблатт называет пространство исходных данных.
Доказательства я естественно рассматривать не буду (см. оригинал), но что нам далее будет важно — схождение перцептрона математически не гарантируется (не гарантируется не означает не будет — при простых входных данных будет, даже если нарушить, речь идет именно о произвольных входных данных) в двух случаях:
1. Если число примеров в обучающей выборке будет больше чем число нейронов в среднем слое (А-элементов)
2. Если у G матрицы детерминант равен нулю
По первой части, все просто, мы всегда можем выставить число А-элементов равным числу примеров в обучающей выборке.
А вот, вторая часть особенно интересна в свете нашего вопроса. Если вы справились с пониманием, что же это за G-матрица, то ясно, что как раз она зависит от входных данных и того какие связи образовались случайно в первом слое.
И теперь мы переходим к вопросу:
Но так как первый слой связей в перцептроне выбирается случайным образом и не обучается, часто возникает мнение, что с равной вероятностью перцептрон может работать, а может не работать при линейно неразделимых исходных данных, и только линейные исходные данные гарантируют его безупречную работу. Другими словами, — матрица перцептрона с равной вероятностью может быть как особенной, так и не особенной. Здесь будет показано, что такое мнение ошибочно. (тут и далее, цитаты из моих научных статей)
Вероятность активности А – элементов
Из определения матрицы А видим, что она бинарная, и принимает значение 1, когда активен соответствующий А – элемент. Нас будет интересовать, какова вероятность появления в матрице единицы и, соответственно, какова вероятность нуля.
Дальше я немного пропущу детали и дам сразу рисунок:
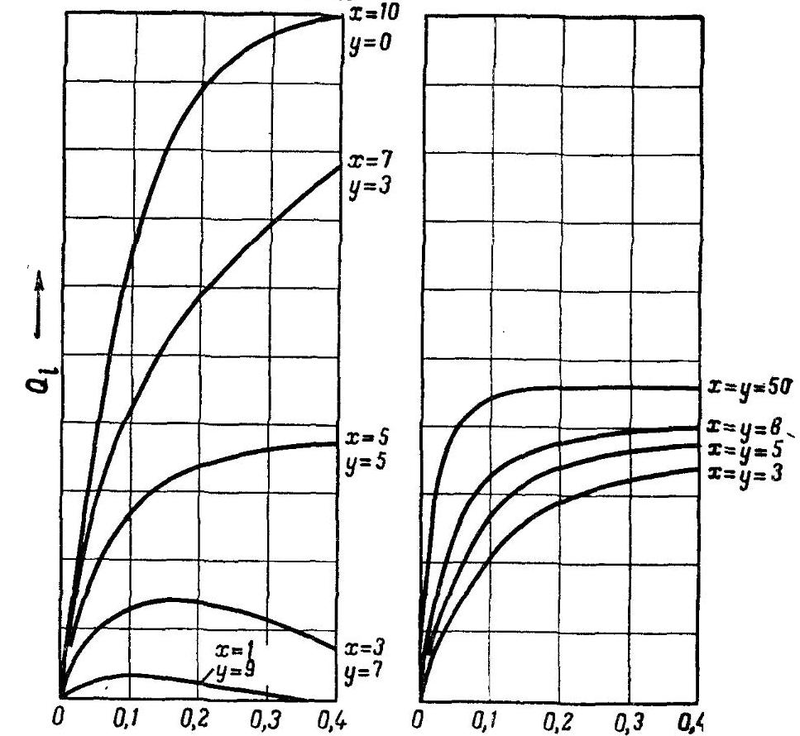
это т.н. Q-функции проанализированные Розенблаттом. В детали я вдаваться не буду, но тут важно, что:
x это число возбуждающих связей в первом слое, подходящие к одному А-элементу (вес +1) и y число тормозящих (вес -1). По оси y на рисунке показана величина этой Q-функции, которая зависит от относительного числа освещенных элементов на сетчатке (1 на входе).
На рисунке показана зависимость вероятности активности А — элемента Qi от величины освещенной площадки сетчатки. Заметим, что для моделей, у которых имеются только возбуждающие связи (y=0) при высоком числе освещенных S — элементов значение Qi приближается к 1. То есть вероятность активности А – элементов находится в прямой зависимости от числа освещенных S — элементов, что плохо влияет на распознавание относительно малых и больших изображений. Как будет показано ниже, это происходит из-за большой вероятности того, что А – матрица будет особенной. Поэтому для стабильности распознавания образов любых геометрических размеров надо так выбрать отношение x:y, чтобы вероятность активности А – элементов как можно меньше бы зависела от числа освещенных S -элементов.
… видно, что при x=y значение Qi остается примерно постоянной во всей области, за исключением очень малого или очень большого числа освещенных S — элементов. А если увеличить общее число связей, то область, в которой Qi остается постоянной, расширяется. При малом пороге и равных x и y приближается к значению 0.5, т.е. равно вероятному возникновению активности А – элемента на произвольный стимул. Таким образом, найдены условия, при которых появление единицы и нуля в матрице А равновероятно.
А этом случае число единиц в матрице А будет описываться биномиальным распределением. Для примера, на следующем рисунке показано распределение числа матриц N в зависимости от количества единиц n в матрице, размером 5х5
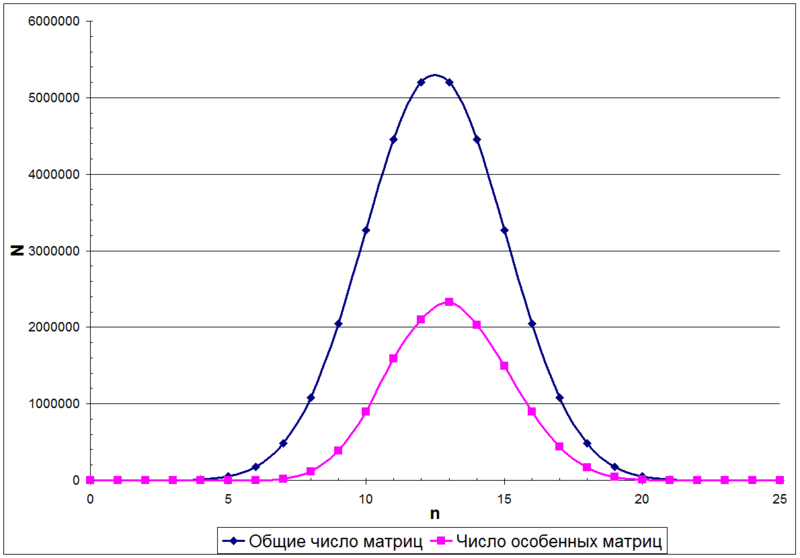
И наконец, какова вероятность того, что А матрица особенная?
Из биноминального распределения можно узнать, как распределено общее число матриц с разным числом единиц в матрице (верхняя кривая на предыдущем рисунке). Но для числа неособенных матриц (нижняя кривая на предыдущем рисунке) математической формулы на данный момент не существует.
Но есть последовательность А055165 [6], дающая вероятность именно того, что матрица размером n x n не особенная. Но посчитать ее можно лишь перебором и это сделано до случаев n <=8. Но последующие значения можно получить методом Монте-Карло…
И вот что получается видно на следующем рисунке (это вероятности появления не особенных матриц в зависимости от их размера):
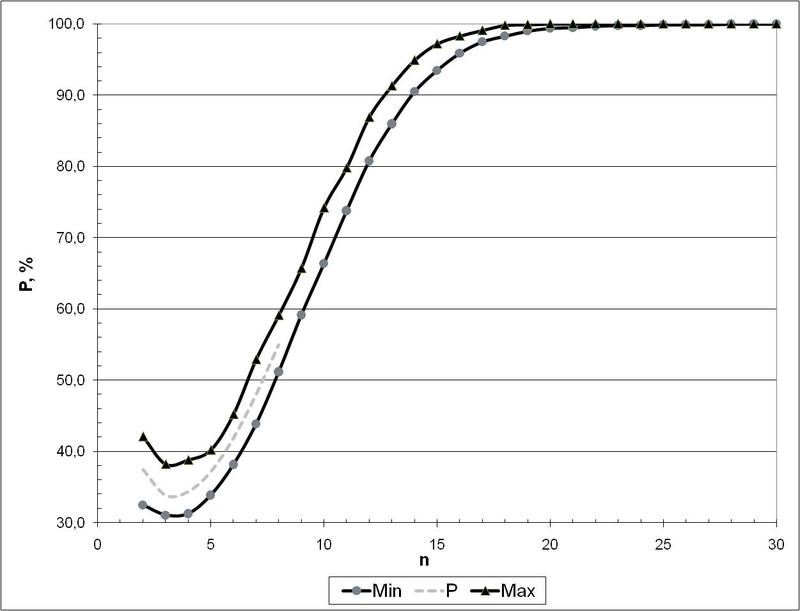
Итак, отсюда видно, что уже при размере матрицы 30 x 30 (т.е. когда число А-элементов 30 и больше) можно говорить почти о 100% уверенности, что случайно полученная матрица будет не особенная. Это и является тем окончательным практическим условием, при котором перцептрон Розенблатта будет формировать пространство, удовлетворяющее гипотезе компактности. Практически же надежнее иметь минимум порядка 100 А-элементов для исключения случая, когда G-матрица становится особенной.
И в заключение. А теперь задайтесь вопросом: а гарантирует ли MLP+BackProp, то о чем я вам здесь изложил в отношении перцептрона Розенблатта? Убедительных доказательств этому я нигде не нашел (только не кидайте ссылки на мат. доказательства сходимости градиентного спуска — это к этому не относится, лучше всего моим оппонентам советую написать свою вразумительную статью на этот счет: "на Хабрахабре приветствуются мысли из своей головы" — будет конструктивнее). Но исходя из наличия проблемы попадания в локальные минимумы при использовании BackProp — тут похоже не все чисто и гладко, как с перцептроном Розенблатта.
upd. что я несколько упустил из вида в изложении, и в ходе диалога мы тут уточнили. Спасибо retran и justserega за наводящие вопросы.
Резюме. В следствиях 1 и 2, говорится, что в определенных условиях решение невозможно. Тут я доказал, что такие условия при n > 30 не наступают (Розенблатт этим не занимался). Но у читателей возникло два вопроса
1. Хорошо А-матрица (а через неё и G) пригодна с высокой вероятностью. Но как это помогает перейти в другое пространство?. Действительно, не очень очевидно. Поясняю. А-матрица это и есть «другое пространство» — пространство признаков. Факт того, что матрица не является особенной и эта матрица на одну размерность больше чем исходная — и есть признак того, что она может быть разделена линейно. (это следует из следствий и теоремы 3)
2. "есть ли доказательства, что алгоритм коррекции ошибки в перцептроне Розенблатта сойдется?". Действительно, теорема №3 говорит только о том, что решение существует. Это уже означает, что это решение существует в пространстве признаков, т.е. после работы случайного первого слоя. Алгоритм же коррекции ошибки обучает второй слой, и существует у Розенблатта теорема №4, в которой он доказывает, что существующие возможные решения (теорема 3, что они вообще есть) могут быть достигнуты именно при применении алгоритма обучения с коррекцией ошибки.
Еще важный момент следует из того, что А-матрица зависит с одной стороны от входных данных, а с другой от случайной матрицы связей. Точнее происходит отображение входной матрицы в матрицу А через случайный оператор (образованные случайно связи ). Если ввести меру случайности, как скорость появления подпоследовательностей которые будут повторяться (псевдослучайность), то окажется: (1) если это совсем не случайная, а построенный по некоторым правилам оператор (т.е. соединения первого слоя), то существенно возрастает вероятность получить А-матрицу особенной (2) если же после умножения входной матрицы на полученную нами псевдослучайность А-матрица имеет не регулярный, а хаотический разброс единиц (назовем это условие R) — то это как раз то, что выше мы в статье анализировали.
Здесь я вам открою мною опробованную вещь. По идеи биномиальной модели случайности при создании связей (это когда берется А-элемент и от него случайно проводятся N возбуждающих и M тормозяцих связей к S-элементам) достаточно, чтобы выполнить условие R. Но чтобы ускорить процесс схождения, можно получить больший уровень хаоса в матрице А. Как это сделать — нам как раз расказывает криптография. Вот такая связь с криптографией тут еще нарисовалась.