Проведя небольшое научное исследование (проще говоря, выполнив поиск на сайте), обнаружил, что на хабре имеется всего две статьи с тегом вычислительная геометрия, причем одна из них оказалась моей. Т.к. в последнее время я несколько заинтересовался этой тематикой, то решил продолжить тему алгоритмической геометрии рассмотрением задачи построения так называемых минимальных выпуклых оболочек. Хотя рисунок справа и дает проницательному хаброчитателю исчерпывающее объяснение того, что это такое, тем не менее под катом будут даны чуть более формальные определения и описаны два классических алгоритма построения минимальных выпуклых оболочек.
Понятие минимальной выпуклой оболочки
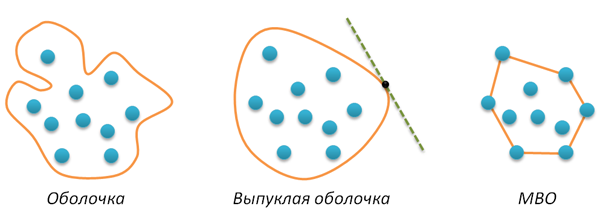
Пусть на плоскости задано конечное множество точек A. Оболочкой этого множества называется любая замкнутая линия H без самопересечений такая, что все точки из A лежат внутри этой кривой. Если кривая H является выпуклой (например, любая касательная к этой кривой не пересекает ее больше ни в одной точке), то соответствующая оболочка также называется выпуклой. Наконец, минимальной выпуклой оболочкой (далее кратко МВО) называется выпуклая оболочка минимальной длины (минимального периметра). Я не проверял (похоже, это можно доказать от противного), но кажется очевидным, что минимальная оболочка просто обязана быть выпуклой. Все введенные понятия иллюстрируются следующим рисунком.
Главной особенностью МВО множества точек A является то, что эта оболочка представляет собой выпуклый многоугольник, вершинами которого являются некоторые точки из A. Поэтому задача поиска МВО в конечном итоге сводится к отбору и упорядочиванию нужных точек из A. Упорядочивание является необходимым по той причине, что выходом алгоритма должен быть многоугольник, т.е. последовательность вершин. Наложим дополнительно условие на порядок расположения вершин — направление обхода многоугольника должно быть положительным (напомню, что положительным называется обход фигуры против часовой стрелки).
Задача построения МВО считается одной из самых простых задач вычислительной геометрии, для нее существует много различных алгоритмов. Ниже мы рассмотрим два таких алгоритма — Грэхема (Graham scan) и Джарвиса (Jarvis march). Их описание иллюстрируется кодом на Питоне. Обоим алгоритмам потребуется функция rotate, побробно описанная в предыдущем моем посте. Напомню, что эта функция определяет, с какой стороны от вектора AB находится точка C (положительное возвращаемое значение соответствует левой стороне, отрицательное — правой).
def rotate(A,B,C):
return (B[0]-A[0])*(C[1]-B[1])-(B[1]-A[1])*(C[0]-B[0])
Алгоритм Грэхема (Graham scan)
Этот алгоритм является трехшаговым. На первом шаге ищется любая точка в A, гарантированно входящая в МВО. Нетрудно сообразить, что такой точкой будет, например, точка с наименьшей x-координатой (самая левая точка в A). Эту точку (будем называть ее стартовой) перемещаем в начало списка, вся дальнейшая работа будет производиться с оставшимися точками. По некоторым соображениям, исходный массив точек A нами меняться не будет, для всех манипуляций с точками будем использовать косвенную адресацию: заведем список P, в котором будут хранится номера точек (их позиции в массиве A). Итак, первый шаг алгоритма заключается в том, чтобы первой точкой в P оказалась точка с наименьшей x-координатой. Код:
def grahamscan(A):
n = len(A) # число точек
P = range(n) # список номеров точек
for i in range(1,n):
if A[P[i]][0]<A[P[0]][0]: # если P[i]-ая точка лежит левее P[0]-ой точки
P[i], P[0] = P[0], P[i] # меняем местами номера этих точек
Второй шаг в алгоритме Грэхема — сортировка всех точек (кроме P[0]-ой), по степени их левизны относительно стартовой точки R=AP[0]. Будем говорить, что B<C, если точка С находится по левую сторону от вектора RB.

Для выпонения такого упорядочивания можно применять любой алгоритм сортировки, основанный на попарном сравнении элементов, например, быструю сортировку. По некоторым причинам (главная из которых — корявость* рук), я буду использовать сортировку вставками.
*я буду очень признателен тем, кто сможет мне объяснить, как применить в данном случае встроенную питоновскую сортировку...
Итак, сортировка вставками (не забываем про косвенную адресацию и про то, что нулевая точка не сортируется):
for i in range(2,n):
j = i
while j>1 and (rotate(A[P[0]],A[P[j-1]],A[P[j]])<0):
P[j], P[j-1] = P[j-1], P[j]
j -= 1
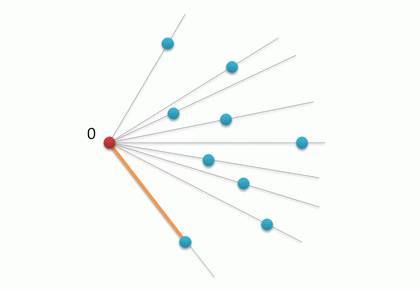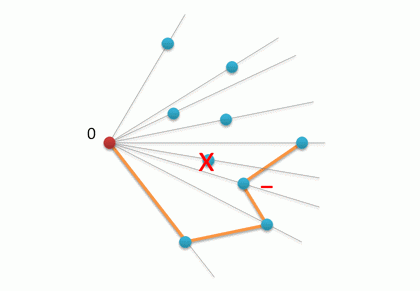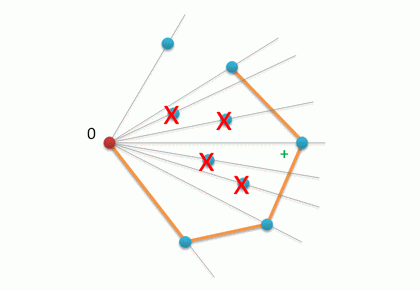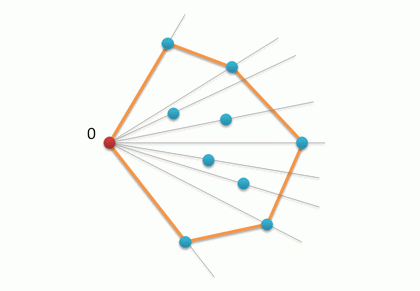
Результат сортировки можно проиллюстрировать следующим рисунком.
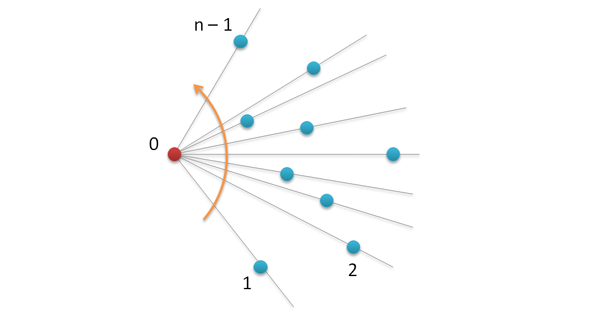
Если мы теперь соединим точки в полученном порядке, то получим многоугольник, который, однако, не является выпуклым.
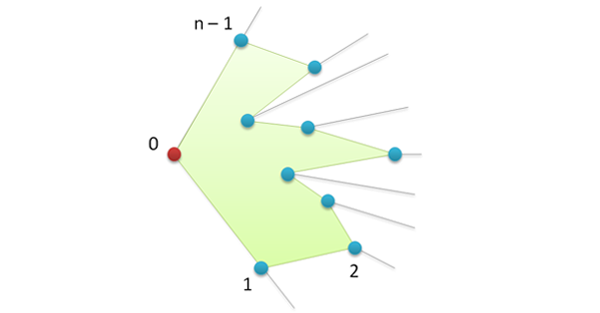
Переходим к третьему действию. Все, что нам осталось сделать, так это срезать углы. Для этого нужно пройтись по всем вершинам и удалить те из них, в которых выполняется правый поворот (угол в такой вершине оказывается больше развернутого). Заводим стек S (реально список) и помещаем в него первые две вершины (они, опять же, гарантированно входят в МВО).
S = [P[0],P[1]]
Затем просматриваем все остальные вершины, и отслеживаем направление поворота в них с точки зрения последних двух вершин в стеке S: если это направление отрицательно, то можно срезать угол удалением из стека последней вершины. Как только поворот оказывается положительным, срезание углов завершается, текущая вершина заносится в стек.
for i in range(2,n):
while rotate(A[S[-2]],A[S[-1]],A[P[i]])<0:
del S[-1] # pop(S)
S.append(P[i]) # push(S,P[i])
В итоге в стеке S (который теперь можно рассматривать, как список) оказывается искомая последовательность вершин, причем в нужной нам ориентации, определяющая МВО заданного множества точек A.
return S
Сложность первого и последнего шагов алгоритма является линейной по n (хотя в последнем случае имеется вложенный цикл, однако, каждая вершина внутри этого цикла ровно один раз заносится в стек, и не более одного раза оттуда удаляется), следовательно, сложность всего алгоритма определяется вторым шагом — сортировкой, именно поэтому сортировка вставкой оказывается не лучшим вариантом при больших n. Если ее заменить на быструю сортировку, то получим суммарную сложность алгоритма O(nlogn). Можно ли улучшить это время? Если алгоритм основан на попарном сравнении точек (как у нас), то доказано, что данная оценка в общем случае не улучшаема. С этой точки зрения алгоритм Грэхема оптимален. Тем не менее у него имеется не очень хорошая особенность — он не является адаптивным в том смысле, что не важно, сколько вершин в итоге войдет в МВО (три, пять, десять или n), все равно время будет линейно-логарифмическим. Такой адаптивностью обладает алгоритм Джарвиса, к рассмотрению которого мы плавно и переходим.
Полный код алгоритма Грэхема
def grahamscan(A):
n = len(A) # число точек
P = range(n) # список номеров точек
for i in range(1,n):
if A[P[i]][0]<A[P[0]][0]: # если P[i]-ая точка лежит левее P[0]-ой точки
P[i], P[0] = P[0], P[i] # меняем местами номера этих точек
for i in range(2,n): # сортировка вставкой
j = i
while j>1 and (rotate(A[P[0]],A[P[j-1]],A[P[j]])<0):
P[j], P[j-1] = P[j-1], P[j]
j -= 1
S = [P[0],P[1]] # создаем стек
for i in range(2,n):
while rotate(A[S[-2]],A[S[-1]],A[P[i]])<0:
del S[-1] # pop(S)
S.append(P[i]) # push(S,P[i])
return S
Алгоритма Джарвиса
Алгоритм Джарвиса (другое название — алгоритм заворачивания подарков) концептуально устроен проще алгоритма Грэхема. Он является двухшаговым и не требует сортировки. Первый шаг точно такой же — нам нужна стартовая точка, которая гарантированно входит в МВО, берем самую левую точку из A.
def jarvismarch(A):
n = len(A)
P = range(n)
for i in range(1,n):
if A[P[i]][0]<A[P[0]][0]:
P[i], P[0] = P[0], P[i]
На втором шаге алгоритма строится МВО. Идея: делаем стартовую вершину текущей, ищем самую правую точку в A относительно текущей вершины, делаем ее текущей и т.д. Процесс завершается, когда текущей вновь окажется стартовая вершина. Как только точка попала в МВО, больше ее можно не учитывать. Поэтому заведем еще один список H, в котором в правильном порядке будут храниться вершины МВО. В этот список сразу же заносим стартовую вершину, а в списке P эту вершину переносим в конец (где мы ее в конце концов найдем и завершим алгоритм).
H = [P[0]]
del P[0]
P.append(H[0])
Теперь организуем бесконечный цикл, на каждой итерации которого ищем самую левую точку из P относительно последней вершины в H. Если эта вершина стартовая, то прерываем цикл, если нет — то переносим найденную вершину из P в H. После завершения цикла в H находится искомая оболочка, которую мы и возвращаем в качестве результата.
while True:
right = 0
for i in range(1,len(P)):
if rotate(A[H[-1]],A[P[right]],A[P[i]])<0:
right = i
if P[right]==H[0]:
break
else:
H.append(P[right])
del P[right]
return H
Хм, мне удалось рассказать об алгоритме Джарвиса, не используя картинок. Следующий рисунок иллюстрирует все!

Оценим сложность алгоритма Джарвиса. Первый шаг линеен по n. Со вторым все интереснее. У нас имеется вложенный цикл, число внешних итераций равно числу вершин h в МВО, число внутренних итераций не превышает n. Следовательно, сложность всего алгоритма равна O(hn). Необычным в этой формуле является то, что сложность определяется не только длиной входных данных, но и длиной выхода (output-sensitive algorithm). А дальше как
**Машина времени вообще полезная штука с точки зрения алгоритмов, любая задача, требующая триллиона лет вычислений, с ее помощью может быть решена практически мгновенно — запускаем программу, садимся в машину времени, «летим» в будущее, считываем результат, возвращаемся назад. Осталось придумать, как обеспечить бесперебойную работу компьютера на пару триллионов лет...
Полный код алгоритма Джарвиса
def jarvismarch(A):
n = len(A)
P = range(n)
# start point
for i in range(1,n):
if A[P[i]][0]<A[P[0]][0]:
P[i], P[0] = P[0], P[i]
H = [P[0]]
del P[0]
P.append(H[0])
while True:
right = 0
for i in range(1,len(P)):
if rotate(A[H[-1]],A[P[right]],A[P[i]])<0:
right = i
if P[right]==H[0]:
break
else:
H.append(P[right])
del P[right]
return H
Вместо заключения
На мой взгляд, задача построения минимальных выпуклых оболочек — хороший способ войти в тему вычислительной геометрии, достаточно легко придумать свой собственный алгоритм (однако, наверняка это будет вариация алгоритма Джарвиса). Утверждается, что приложений у этой задачи много, большая их часть связана с распознаванием образов, кластеризацией и т.п. Кроме того, задача построения МВО используется в качестве вспомогательного средства при решении более сложных задач вычислительной геометрии. Да, стоит отметить, что у этой задачи имеется весьма интересное трехмерное обобщение.
Спасибо всем за внимание!