Однажды, пролистывая популярный Q&A по математике (math.stackexchange.com), я обнаружил вопрос про расчет мультиномиальных коэффициентов и он меня заинтересовал. На заметку, для тех, кто не знает что это такое, существует статья в википедии. Итак, нужно вычислить следующее выражение:
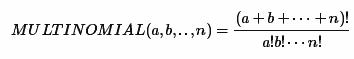
Казалось, зачем на хабре выкладывать решение такой простой задачи? Ответ заключается в том, что самый простой наивный способ, заключающийся в перемножении факториала суммы с последующим делением его на произведение факториалов, не подойдет из-за того, что промежуточные вычисления выйдут за разрядную сетку типа uint и даже ulong, хотя результат может оказаться в пределах значений этих типов. Мне понравилась эта задача, и я сразу же сел за ее решение и придумал три способа. Остальные два способа я позаимствовал из других ответов. Итак, статья будет об описании и сравнении всех реализованных мною методов на C# под .NET.
Далее я опишу каждый метод.
Конечно же первое, что пришло на ум — это использование специального типа BigInteger, способного хранить числа с произвольным количеством цифр. Но это, во-первых, не спортивно, а, во-вторых, не все языки имеют поддержку таких типов (хотя конечно можно самому написать), зато данный способ уж точно всегда возвращает правильный результат, в отличие от других методов, в которых присутствует округление. Кстати, данное свойство позволяет тестировать точность остальных методов, о которой будет рассказано позже.
Код данного метода ничем не отличается от наивной реализации, за исключением того, что вместо типов uint везде стоит BigInteger. Поэтому особого интереса не представляет.
Заключается в подсчете всех мультиномиальных коэффициентов от заданных аргументов в Microsoft Excel, wolframalpha.com или других сторонних программах/сервисах и занесением рассчитанных коэффициентов в исходный код или отдельный файл. Недостатки данного подхода очевидны: большой расход памяти, расчет коэффициентов не от всех допустимых возможных значений аргументов. Хотя производительность данного метода, конечно, на высоте. Так или иначе, данный метод мною даже не был реализован.
Данный метод заключается в разложении выражения мультиномиального коэффициента на произведение нескольких биномиальных коэффициентов по следующей формуле:

Но здесь, опять таки, возможно переполнение уже при вычислении последних биномиальных коэффициентов. Для того, чтобы это не произошло, используется алгоритм рекурсивного вычисления каждого биномиального коэффициента по следующие формуле:

Код на C# же выглядит следующим образом:
Данный способ заключается в разложении исходной формулы на сумму и разность логарифмов следующим образом:

В самом конце, естественно, необходимо возвести e в получившуюся степень, что и будет являться результатом. Также была выполнена небольшая оптимизация, которая заключалась в отбрасывании максимального факториала знаменателя из числителя и знаменателя. В целях ускорения последующих вычислений, все логарифмы кэшируются в список (в конце статьи тестируется производительность данной оптимизации).
Данный способ почти не отличается от предыдущего за исключением того, что вместо разложения логарифма факториала на сумму логарифмов, используется специальная функция логарифма от гамма функции, реализация которой была взята из alglib. На самом деле есть и другие, более короткие реализации (например в Math.NET), но мне показалось, что если в alglib размер кода реализации самый большой, то сама реализация является самой точной.
Мой метод заключается в применение последовательности следующих операций:
Тестирование всех методов проходило в два этапа: это тест на максимальное число, которое может быть вычислено каким-либо методом без переполнения и ошибок округления, а также тест на скорость.
Легко доказать, что мультиномиального коэффициент — коммутативная операция, т.е. например M(a, b, c) = M(a, c, b) = M(c, b, a) и т.д. А значит для проверки всех комбинаций чисел с заданным количеством аргументов можно использовать перестановки с повторениями (permutations with repetitions). Для этих целей была использована библиотека для генерации данных и других комбинаций из codeproject. Таким образом, все комбинации были выстроены в лексикографическом порядке.
На двух графиках ниже показана зависимость номера перестановки максимально возможного вычислимого числа от количества аргументов в мультиномиальной функции.
Для лучшего понимания объясню первое множество значений с количеством аргументов 2:
В тесте выше видно, что например максимальное ulong значение, которое может быть вычислено с помощью логарифмов, это 59481941558292. Оно было вычислено из аргументов 6 и 588, что соответствует перестановке 6481, если генерировать их в лексикографическом порядке. Данное число и отображено на зеленом графике. Термин rounding говорит о том, что если взять следующую перестановку, т.е. (6,589), то данный метод будет считать мультиномиальный коэффициент с ошибкой 1. А термин overflow говорит о том, что если вычислять коэффициент от следующей перестановки (например если взять (1,63) для Binom), то где-то внутри метода произойдет переполнение.
Так как разница между первыми и последними номерами перестановок слишком велика, я разбил график на две части (с количество аргументов 2-10 и 11-20). На двадцати одном и более аргументе все функции дают неверный результат даже на первой перестановке (оно и понятно, ведь Multinomial(1,1,...,1) = 21!, а это число больше, чем максимальное ulong. Дальнейшее увеличение любого аргумента только увеличит результат. Данное утверждение я оставлю без доказательства).
Оранжевый график показывает идеальный результат, т.е. вообще самый максимальный ulong, который только может быть вычислен мультиномиальной функцией с заданным количеством аргументов. Т.е. дальнейший инкремент перестановки приведет к тому, что результат выйдет за пределы ulong типа. Значения для этого графика были вычислены с помощью больших целых чисел, о которых говорилось в самом начале статьи.


Итак, мой метод, как это видно из обоих графиков, позволяет вычислять больший коэффициент практически во всех случаях, за исключением 12 и 13 аргументов. Несмотря на большие ожидания от биномиальных коэффициентов, оказалось, что они покрывают небольшой набор значений в случае их небольшого количества (от 2 до 8). Начиная с 9, они начинают охватывать больший диапазон, чем Log и LogGamma, а на 12 и 13 даже обходят мой метод. После 13 они рассчитываются идеально, впрочем как они рассчитываются и моем методе.
Методы Log и LogGamma охватывают примерно одинаковый диапазон, особенно при большом количестве аргументах. То, что Log все-таки опережает LogGamma на 1-12 видимо объясняется тем, что функция Log(N!) рассчитывается менее точно, чем сумма вещественных чисел (логарифмов). И простой метод даже оказался эффективней логарифмов на 15-19 количестве аргументов.
Стоит отметить, что картина особо не изменялась при изменении абсолютной ошибки Max Error (т.е. максимально допустимой ошибки при округлении), поэтому другие графики с Max Error равной 10 и 100 я приводить не стал.
Для замера скорости каждого метода я использовал два тестовых набора. Первый покрывает довольно большие числа, на котором простой метод Naive вылетает с ошибкой overflow, поэтому он не учитывался. BigInteger также не учитывался. Каждый набор прогонялся 20000 раз, и данное время расчета и замерялось.
Также данные методы были протестированы с предварительным расчетом (prefetch) и без. Это актуально только для методов Log и LogGamma, поскольку только в них используются заранее рассчитанные логарифмы и логарифмы от факториалов.

Как видим, мой метод здесь оказался хуже остальных методов раза в 3.
То, что Binom рассчитал все быстрее всех объясняется тем, что в нем используется только целочисленная арифметика, которая априори быстрее.
Небольшое опережение LogGamma по сравнению с Log объясняется тем, что в нем повторно не складываются логарифмы, а запоминается сразу логарифм от факториала, т.е. например вместо Ln(2) + Ln(3) + Ln(4) используется Ln(4!).
Также видно, что prefetch, как оказалось, практически не влияет на скорость Log и LogGamma, а это говорит о том, что видимо вычисление данных функций сопоставимо с извлечением уже вычисленных значений или о том, что время их вычисления слишком мало, по сравнению с суммарным временем остальных операций.
Следующий набор предназначался даже для самой простой наивной функции. Большие числа также были включены в следующую диаграмму:
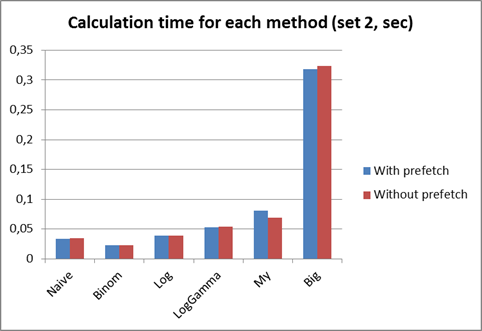
Как видно, в данном случае мой метод показал меньшее отставание от остальных функций (за исключением Big), а метод с большими числами оказался раза в 4 хуже даже моего метода. Это объясняется тем, что реализация больших чисел в .NET далеко от идеала. Декомпиляция некоторых методов библиотеки System.Numerics с помощью ILSpy подтвердила мои предположения (в коде видно, что даже для такой простой операции, как сложение, используется большое количество безопасного кода):
Эксперименты показали, что мой метод оказался лучше остальных в контексте максимально вычислимого числа (но при этом все равно хуже идеального), но хуже в контексте производительности (но при этом гораздо лучше реализации с большими числами в .NET). Также можно сделать вывод, что реализация арифметики больших чисел далека от идеала в .NET и если есть возможность заменить ее другим методом, то лучше использовать его.
Метод с биномиальным коэффициентами оказался самым быстрым, даже быстрее простой реализации, но это вполне очевидно, поскольку в нем используется только целочисленная арифметика. С другой стороны, данный метод охватывает не такой уж большой диапазон значений, особенно при малом количестве аргументов.
Также эксперименты показали, что повторное использование вычисленных значений логарифмов и логарифмов от факториалов не дают существенного выигрыша в производительности, так что их можно не использовать.
Я надеюсь, что проделанная работа с экспериментами окажется интересной и полезной не только для меня, поэтому я выкладываю исходный код вместе с юнит-тестами и тестами на github: Multinimonal-Coefficient.
UPDATE

Казалось, зачем на хабре выкладывать решение такой простой задачи? Ответ заключается в том, что самый простой наивный способ, заключающийся в перемножении факториала суммы с последующим делением его на произведение факториалов, не подойдет из-за того, что промежуточные вычисления выйдут за разрядную сетку типа uint и даже ulong, хотя результат может оказаться в пределах значений этих типов. Мне понравилась эта задача, и я сразу же сел за ее решение и придумал три способа. Остальные два способа я позаимствовал из других ответов. Итак, статья будет об описании и сравнении всех реализованных мною методов на C# под .NET.
- Большие числа
- Табличный способ
- Перемножение биномиальных коэффициентов
- Сумма и разность логарифмов
- Сумма и разность фукнций «логарифм факториала»
- Мой способ
Далее я опишу каждый метод.
Большие числа
Конечно же первое, что пришло на ум — это использование специального типа BigInteger, способного хранить числа с произвольным количеством цифр. Но это, во-первых, не спортивно, а, во-вторых, не все языки имеют поддержку таких типов (хотя конечно можно самому написать), зато данный способ уж точно всегда возвращает правильный результат, в отличие от других методов, в которых присутствует округление. Кстати, данное свойство позволяет тестировать точность остальных методов, о которой будет рассказано позже.
Код данного метода ничем не отличается от наивной реализации, за исключением того, что вместо типов uint везде стоит BigInteger. Поэтому особого интереса не представляет.
BigInteger source
public static BigInteger BigAr(uint[] numbers)
{
BigInteger numbersSum = 0;
foreach (var number in numbers)
numbersSum += number;
BigInteger nominator = Factorial(numbersSum);
BigInteger denominator = 1;
foreach (var number in numbers)
denominator *= Factorial(new BigInteger(number));
return nominator / denominator;
}
public static BigInteger Factorial(BigInteger n)
{
BigInteger result = 1;
for (ulong i = 1; i <= n; i++)
result = result * i;
return result;
}
Табличный метод
Заключается в подсчете всех мультиномиальных коэффициентов от заданных аргументов в Microsoft Excel, wolframalpha.com или других сторонних программах/сервисах и занесением рассчитанных коэффициентов в исходный код или отдельный файл. Недостатки данного подхода очевидны: большой расход памяти, расчет коэффициентов не от всех допустимых возможных значений аргументов. Хотя производительность данного метода, конечно, на высоте. Так или иначе, данный метод мною даже не был реализован.
Биномиальные коэффициенты
Данный метод заключается в разложении выражения мультиномиального коэффициента на произведение нескольких биномиальных коэффициентов по следующей формуле:
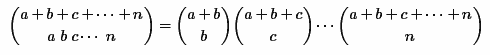
Но здесь, опять таки, возможно переполнение уже при вычислении последних биномиальных коэффициентов. Для того, чтобы это не произошло, используется алгоритм рекурсивного вычисления каждого биномиального коэффициента по следующие формуле:
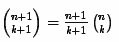
Код на C# же выглядит следующим образом:
Binomial source
public static ulong BinomAr(uint[] numbers)
{
if (numbers.Length == 1)
return 1;
ulong result = 1;
uint sum = numbers[0];
for (int i = 1; i < numbers.Length; i++)
{
sum += numbers[i];
result *= Binominal(sum, numbers[i]);
}
return result;
}
public static ulong Binominal(ulong n, ulong k)
{
ulong r = 1;
ulong d;
if (k > n) return 0;
for (d = 1; d <= k; d++)
{
r *= n--;
r /= d;
}
return r;
}
Логарифмы
Данный способ заключается в разложении исходной формулы на сумму и разность логарифмов следующим образом:
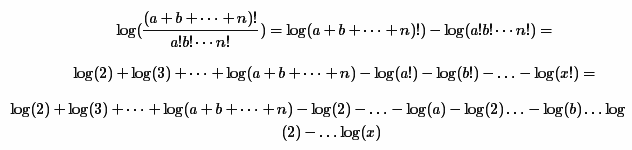
В самом конце, естественно, необходимо возвести e в получившуюся степень, что и будет являться результатом. Также была выполнена небольшая оптимизация, которая заключалась в отбрасывании максимального факториала знаменателя из числителя и знаменателя. В целях ускорения последующих вычислений, все логарифмы кэшируются в список (в конце статьи тестируется производительность данной оптимизации).
Log source
static List<double> Logarithms = new List<double>();
public static ulong Log(params uint[] numbers)
{
return LogAr(numbers);
}
public static ulong LogAr(uint[] numbers)
{
int maxNumber = (int)numbers.Max();
uint numbersSum = 0;
foreach (var number in numbers)
numbersSum += number;
double sum = 0;
for (int i = 2; i <= numbersSum; i++)
{
if (i <= maxNumber)
{
if (i - 2 >= Logarithms.Count)
{
var log = Math.Log(i);
Logarithms.Add(log);
}
}
else
{
if (i - 2 < Logarithms.Count)
sum += Logarithms[i - 2];
else
{
var log = Math.Log(i);
Logarithms.Add(log);
sum += log;
}
}
}
var maxNumberFirst = false;
foreach (var number in numbers)
if (number == maxNumber && !maxNumberFirst)
maxNumberFirst = true;
else
for (int i = 2; i <= number; i++)
sum -= Logarithms[i - 2];
return (ulong)Math.Round(Math.Exp(sum));
}
Логарифмы от факториалов
Данный способ почти не отличается от предыдущего за исключением того, что вместо разложения логарифма факториала на сумму логарифмов, используется специальная функция логарифма от гамма функции, реализация которой была взята из alglib. На самом деле есть и другие, более короткие реализации (например в Math.NET), но мне показалось, что если в alglib размер кода реализации самый большой, то сама реализация является самой точной.
LogGamma source
static Dictionary<uint, double> LnFacts = new Dictionary<uint, double>();
public static ulong LogGammaAr(uint[] numbers)
{
int maxNumber = (int)numbers.Max();
double value;
double denom = 0;
uint numbersSum = 0;
foreach (var number in numbers)
{
numbersSum += number;
if (LnFacts.TryGetValue(number, out value))
denom += value;
else
{
value = LnGamma(number + 1);
LnFacts.Add(number, value);
denom += value;
}
}
double numer;
if (LnFacts.TryGetValue(numbersSum, out value))
numer = value;
else
{
value = LnGamma(numbersSum + 1);
LnFacts.Add(numbersSum, value);
numer = value;
}
return (ulong)Math.Round(Math.Exp(numer - denom));
}
public static double LnGamma(double x)
{
double sign = 1;
return LnGamma(x, ref sign);
}
public static double LnGamma(double x, ref double sgngam)
{
double result = 0;
double a = 0;
double b = 0;
double c = 0;
double p = 0;
double q = 0;
double u = 0;
double w = 0;
double z = 0;
int i = 0;
double logpi = 0;
double ls2pi = 0;
double tmp = 0;
sgngam = 0;
sgngam = 1;
logpi = 1.14472988584940017414;
ls2pi = 0.91893853320467274178;
if ((double)(x) < (double)(-34.0))
{
q = -x;
w = LnGamma(q, ref tmp);
p = (int)Math.Floor(q);
i = (int)Math.Round(p);
if (i % 2 == 0)
{
sgngam = -1;
}
else
{
sgngam = 1;
}
z = q - p;
if ((double)(z) > (double)(0.5))
{
p = p + 1;
z = p - q;
}
z = q * Math.Sin(Math.PI * z);
result = logpi - Math.Log(z) - w;
return result;
}
if ((double)(x) < (double)(13))
{
z = 1;
p = 0;
u = x;
while ((double)(u) >= (double)(3))
{
p = p - 1;
u = x + p;
z = z * u;
}
while ((double)(u) < (double)(2))
{
z = z / u;
p = p + 1;
u = x + p;
}
if ((double)(z) < (double)(0))
{
sgngam = -1;
z = -z;
}
else
{
sgngam = 1;
}
if ((double)(u) == (double)(2))
{
result = Math.Log(z);
return result;
}
p = p - 2;
x = x + p;
b = -1378.25152569120859100;
b = -38801.6315134637840924 + x * b;
b = -331612.992738871184744 + x * b;
b = -1162370.97492762307383 + x * b;
b = -1721737.00820839662146 + x * b;
b = -853555.664245765465627 + x * b;
c = 1;
c = -351.815701436523470549 + x * c;
c = -17064.2106651881159223 + x * c;
c = -220528.590553854454839 + x * c;
c = -1139334.44367982507207 + x * c;
c = -2532523.07177582951285 + x * c;
c = -2018891.41433532773231 + x * c;
p = x * b / c;
result = Math.Log(z) + p;
return result;
}
q = (x - 0.5) * Math.Log(x) - x + ls2pi;
if ((double)(x) > (double)(100000000))
{
result = q;
return result;
}
p = 1 / (x * x);
if ((double)(x) >= (double)(1000.0))
{
q = q + ((7.9365079365079365079365 * 0.0001 * p - 2.7777777777777777777778 * 0.001) * p + 0.0833333333333333333333) / x;
}
else
{
a = 8.11614167470508450300 * 0.0001;
a = -(5.95061904284301438324 * 0.0001) + p * a;
a = 7.93650340457716943945 * 0.0001 + p * a;
a = -(2.77777777730099687205 * 0.001) + p * a;
a = 8.33333333333331927722 * 0.01 + p * a;
q = q + a / x;
}
result = q;
return result;
}
Мой метод
Мой метод заключается в применение последовательности следующих операций:
- Подсчет степеней чисел в знаменателе. Например для аргументов (5, 5, 5) они будет следующими: denomFactorPowers[6] = {0, 0, 2, 2, 2, 2}. Т.е. если перемножить все факториалы в знаменателе, то получится 3^2 * 4^2 * 5^2 * 6^2. А степень именно вторая, потому что часть степеней сократилось с числителем, и в числителе стало 6 *… * 15, вместо 1 *… * 15.
- Инициализация result = 1 (результат функции); tempDenom = 1 (результат перемножения чисел в знаменателе); currentFactor (текущий множитель в знаменателе).
- Цикл переменной i по всем оставшимся числам числителя (maxNumber + 1… numbersSum).
- Вычисление tempDenom до тех пор, пока tempDenom < result и в знаменателе не закончились числа (currentFactor < denomFactorPowers.Length).
- Если tempDenom > result или в знаменателе закончились числа (currentFactor >= denomFactorPowers.Length), то вычислять результат следующим образом: result = result / tempDenom * i. Данная методика позволяет вычислять результат максимально точно и без переполнения, потому что result / tempDenom → 1.
My method source
public static ulong MyAr(uint[] numbers)
{
uint numbersSum = 0;
foreach (var number in numbers)
numbersSum += number;
uint maxNumber = numbers.Max();
var denomFactorPowers = new uint[maxNumber + 1];
foreach (var number in numbers)
for (int i = 2; i <= number; i++)
denomFactorPowers[i]++;
for (int i = 2; i < denomFactorPowers.Length; i++)
denomFactorPowers[i]--; // reduce with nominator;
uint currentFactor = 2;
uint currentPower = 1;
double result = 1;
for (uint i = maxNumber + 1; i <= numbersSum; i++)
{
uint tempDenom = 1;
while (tempDenom < result && currentFactor < denomFactorPowers.Length)
{
if (currentPower > denomFactorPowers[currentFactor])
{
currentFactor++;
currentPower = 1;
}
else
{
tempDenom *= currentFactor;
currentPower++;
}
}
result = result / tempDenom * i;
}
return (ulong)Math.Round(result);
}
Тестирование
Тестирование всех методов проходило в два этапа: это тест на максимальное число, которое может быть вычислено каким-либо методом без переполнения и ошибок округления, а также тест на скорость.
Тест на максимально возможное вычислимое число
Легко доказать, что мультиномиального коэффициент — коммутативная операция, т.е. например M(a, b, c) = M(a, c, b) = M(c, b, a) и т.д. А значит для проверки всех комбинаций чисел с заданным количеством аргументов можно использовать перестановки с повторениями (permutations with repetitions). Для этих целей была использована библиотека для генерации данных и других комбинаций из codeproject. Таким образом, все комбинации были выстроены в лексикографическом порядке.
На двух графиках ниже показана зависимость номера перестановки максимально возможного вычислимого числа от количества аргументов в мультиномиальной функции.
Для лучшего понимания объясню первое множество значений с количеством аргументов 2:
Arg count: 2
Naive(1,19) = 20; #18; overflow
Binom(1,61) = 62; #60; overflow
LogGamma(5,623) = 801096582000; #4612; rounding(error = 1)
Log(6,588) = 59481941558292; #5572; rounding(error = 1)
My(7,503) = 1708447057008120; #6481; rounding(error = 1)
Big(8,959) = 18419736117819661560; #7930
В тесте выше видно, что например максимальное ulong значение, которое может быть вычислено с помощью логарифмов, это 59481941558292. Оно было вычислено из аргументов 6 и 588, что соответствует перестановке 6481, если генерировать их в лексикографическом порядке. Данное число и отображено на зеленом графике. Термин rounding говорит о том, что если взять следующую перестановку, т.е. (6,589), то данный метод будет считать мультиномиальный коэффициент с ошибкой 1. А термин overflow говорит о том, что если вычислять коэффициент от следующей перестановки (например если взять (1,63) для Binom), то где-то внутри метода произойдет переполнение.
Так как разница между первыми и последними номерами перестановок слишком велика, я разбил график на две части (с количество аргументов 2-10 и 11-20). На двадцати одном и более аргументе все функции дают неверный результат даже на первой перестановке (оно и понятно, ведь Multinomial(1,1,...,1) = 21!, а это число больше, чем максимальное ulong. Дальнейшее увеличение любого аргумента только увеличит результат. Данное утверждение я оставлю без доказательства).
Оранжевый график показывает идеальный результат, т.е. вообще самый максимальный ulong, который только может быть вычислен мультиномиальной функцией с заданным количеством аргументов. Т.е. дальнейший инкремент перестановки приведет к тому, что результат выйдет за пределы ulong типа. Значения для этого графика были вычислены с помощью больших целых чисел, о которых говорилось в самом начале статьи.
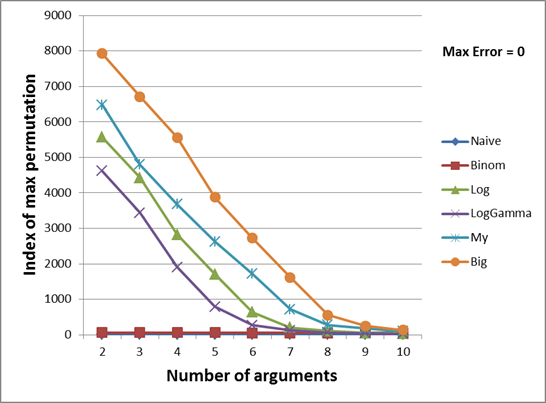
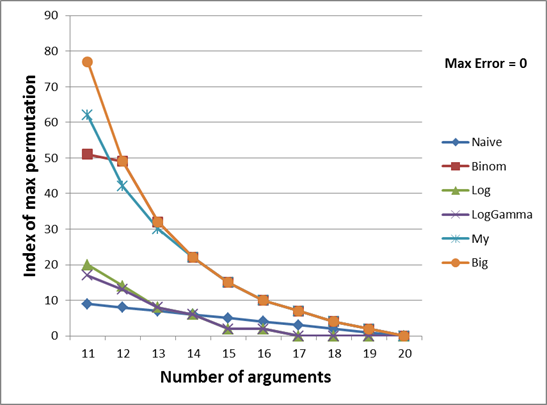
Итак, мой метод, как это видно из обоих графиков, позволяет вычислять больший коэффициент практически во всех случаях, за исключением 12 и 13 аргументов. Несмотря на большие ожидания от биномиальных коэффициентов, оказалось, что они покрывают небольшой набор значений в случае их небольшого количества (от 2 до 8). Начиная с 9, они начинают охватывать больший диапазон, чем Log и LogGamma, а на 12 и 13 даже обходят мой метод. После 13 они рассчитываются идеально, впрочем как они рассчитываются и моем методе.
Методы Log и LogGamma охватывают примерно одинаковый диапазон, особенно при большом количестве аргументах. То, что Log все-таки опережает LogGamma на 1-12 видимо объясняется тем, что функция Log(N!) рассчитывается менее точно, чем сумма вещественных чисел (логарифмов). И простой метод даже оказался эффективней логарифмов на 15-19 количестве аргументов.
Стоит отметить, что картина особо не изменялась при изменении абсолютной ошибки Max Error (т.е. максимально допустимой ошибки при округлении), поэтому другие графики с Max Error равной 10 и 100 я приводить не стал.
Тест производительности методов
Для замера скорости каждого метода я использовал два тестовых набора. Первый покрывает довольно большие числа, на котором простой метод Naive вылетает с ошибкой overflow, поэтому он не учитывался. BigInteger также не учитывался. Каждый набор прогонялся 20000 раз, и данное время расчета и замерялось.
Также данные методы были протестированы с предварительным расчетом (prefetch) и без. Это актуально только для методов Log и LogGamma, поскольку только в них используются заранее рассчитанные логарифмы и логарифмы от факториалов.
Первый тестовый набор аргументов
(1, 1)
(1, 2)
(2, 1)
(2, 2)
(5, 5, 5)
(10, 10, 10)
(5, 10, 15)
(6, 6, 6, 6)
(5, 6, 7, 8)
(2, 3, 4, 5, 7)

Как видим, мой метод здесь оказался хуже остальных методов раза в 3.
То, что Binom рассчитал все быстрее всех объясняется тем, что в нем используется только целочисленная арифметика, которая априори быстрее.
Небольшое опережение LogGamma по сравнению с Log объясняется тем, что в нем повторно не складываются логарифмы, а запоминается сразу логарифм от факториала, т.е. например вместо Ln(2) + Ln(3) + Ln(4) используется Ln(4!).
Также видно, что prefetch, как оказалось, практически не влияет на скорость Log и LogGamma, а это говорит о том, что видимо вычисление данных функций сопоставимо с извлечением уже вычисленных значений или о том, что время их вычисления слишком мало, по сравнению с суммарным временем остальных операций.
Второй тестовый набор аргументов
Следующий набор предназначался даже для самой простой наивной функции. Большие числа также были включены в следующую диаграмму:
(1, 1)
(1, 2)
(2, 1)
(2, 2)
(5, 5, 5)
(1, 1, 1, 1, 1, 1, 1, 1, 2)
(1, 2, 3, 4, 5, 4)

Как видно, в данном случае мой метод показал меньшее отставание от остальных функций (за исключением Big), а метод с большими числами оказался раза в 4 хуже даже моего метода. Это объясняется тем, что реализация больших чисел в .NET далеко от идеала. Декомпиляция некоторых методов библиотеки System.Numerics с помощью ILSpy подтвердила мои предположения (в коде видно, что даже для такой простой операции, как сложение, используется большое количество безопасного кода):
Операция сложения для BigInteger в .NET
public static BigInteger operator +(BigInteger left, BigInteger right)
{
if (right.IsZero)
{
return left;
}
if (left.IsZero)
{
return right;
}
int num = 1;
int num2 = 1;
BigIntegerBuilder bigIntegerBuilder = new BigIntegerBuilder(left, ref num);
BigIntegerBuilder bigIntegerBuilder2 = new BigIntegerBuilder(right, ref num2);
if (num == num2)
{
bigIntegerBuilder.Add(ref bigIntegerBuilder2);
}
else
{
bigIntegerBuilder.Sub(ref num, ref bigIntegerBuilder2);
}
return bigIntegerBuilder.GetInteger(num);
}
...
public void Add(ref BigIntegerBuilder reg)
{
if (reg._iuLast == 0)
{
this.Add(reg._uSmall);
return;
}
if (this._iuLast != 0)
{
this.EnsureWritable(Math.Max(this._iuLast, reg._iuLast) + 1, 1);
int num = reg._iuLast + 1;
if (this._iuLast < reg._iuLast)
{
num = this._iuLast + 1;
Array.Copy(reg._rgu, this._iuLast + 1, this._rgu, this._iuLast + 1, reg._iuLast - this._iuLast);
this._iuLast = reg._iuLast;
}
uint num2 = 0u;
for (int i = 0; i < num; i++)
{
num2 = BigIntegerBuilder.AddCarry(ref this._rgu[i], reg._rgu[i], num2);
}
if (num2 != 0u)
{
this.ApplyCarry(num);
}
return;
}
uint uSmall = this._uSmall;
if (uSmall == 0u)
{
this = new BigIntegerBuilder(ref reg);
return;
}
this.Load(ref reg, 1);
this.Add(uSmall);
}
Заключение
Эксперименты показали, что мой метод оказался лучше остальных в контексте максимально вычислимого числа (но при этом все равно хуже идеального), но хуже в контексте производительности (но при этом гораздо лучше реализации с большими числами в .NET). Также можно сделать вывод, что реализация арифметики больших чисел далека от идеала в .NET и если есть возможность заменить ее другим методом, то лучше использовать его.
Метод с биномиальным коэффициентами оказался самым быстрым, даже быстрее простой реализации, но это вполне очевидно, поскольку в нем используется только целочисленная арифметика. С другой стороны, данный метод охватывает не такой уж большой диапазон значений, особенно при малом количестве аргументов.
Также эксперименты показали, что повторное использование вычисленных значений логарифмов и логарифмов от факториалов не дают существенного выигрыша в производительности, так что их можно не использовать.
Я надеюсь, что проделанная работа с экспериментами окажется интересной и полезной не только для меня, поэтому я выкладываю исходный код вместе с юнит-тестами и тестами на github: Multinimonal-Coefficient.
UPDATE
- Обновил метод с биномиальными коэффициентами: ссылка, автор: Mrrl
- Добавлен метод с разложением на степени простых чисел: ссылка, автор: Mrrl
- Добавлен метод с расчетом комбинаций коэффициентов, полученных при разложении степени суммы на слагаемые: описание и исходники