Этот алгоритм является улучшенным алгоритмом поиска пути A*. JPS ускоряет поиск пути, “перепрыгивая” многие места, которые должны быть просмотрены. В отличие от подобных алгоритмов JPS не требует предварительной обработки и дополнительных затрат памяти. Данный алгоритм представлен в 2011 году, а в 2012 получил высокие отклики. Что из себя представляет данный алгоритм и его реализацию можно прочитать дальше в статье.
Алгоритм работает на неориентированном графе единой стоимости. Каждое поле карты имеет <= 8 соседей, которые могут быть проходимы или же нет. Каждый шаг по направлению (по вертикали или по горизонтали) имеет стоимость 1; шаг по диагонали имеет стоимость √2. Движения через препятствия запрещены. Обозначение относится к одному из восьми направлений движения (вверх, вниз, влево и т.д.).
“Прыжковые точки” позволяют ускорить алгоритм поиска пути, рассматривая только “необходимые” точки. Такие точки могут быть описаны двумя простыми правилами выбора соседей при рекурсивном поиске: одно правило для прямолинейного движения и другое – для диагонального. В обоих случаях необходимо доказать, что исключая из набора ближайших соседей вокруг точки, найдётся оптимальный путь из предка текущей точки до каждого из соседей, и этот путь не будет содержать в себе посещенную точку. Рассмотрим случай 1, который отражает основную идею:
Случай 1: Отсечённый сосед
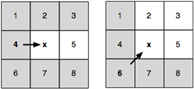
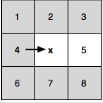
Х – текущая рассматриваемая точка. Стрелка указывает направление движения. И там и там можно сразу отсечь соседей, выделенных серым, т.к. туда можно попасть по оптимальному пути из p(x), никогда не проходя через x.
Будем ссылаться на множество точек, которые остаются после отсечения настоящих соседей текущей точки. Они отмечены белыми на рисунке. В идеале, мы хотим учитывать только настоящих соседей во время просмотра. Тем не менее, в некоторых случаях, наличие препятствий может означать, что мы должны также рассмотреть небольшой набор до K дополнительных точек (0 ≤ K ≤ 2). Мы говорим, что это точки вынужденных соседей текущей позиции.
Случай 2: Принуждённый сосед
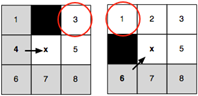
Х – текущая рассматриваемая точка. Стрелка указывает направление движения. Обратите внимание, что, когда х находится рядом с препятствием, выделенные соседи не могут быть отсечены, любой альтернативный оптимальный путь от p(х) в каждом из этих узлов, блокируется.
Эти случаи применяются следующим образом: вместо создания “вынужденных” и “естественных” соседей мы рекурсивно отсекаем список соседей вокруг каждой точки. Таким образом наша цель заключается в ликвидации “симметрии”, рекурсивно “перепрыгивая” через все точки, в которые можно попасть по оптимальному пути, который не проходил через текущую позицию. Рекурсия останавливается при попадании на препятствие или нашли так называемую “прыжковую точку-преемник” (jump point successor). Прыжковые точки интересны тем, что они имеют соседей, которые не могут быть достигнуты альтернативным путём: оптимальный путь должен идти через текущую точку. Таким образом g(y) = g(x) + dist(x; y) – стоимость перемещения.
Для обеспечения оптимальности необходимо только определиться как выбирать соседей (сначала линейные, затем диагональные).
Рассмотрим пример:
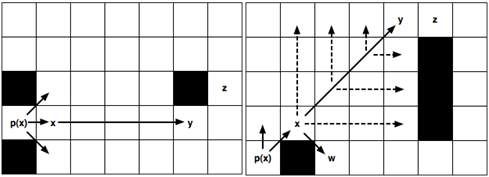
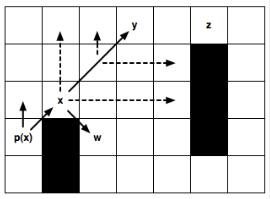
Здесь добавляется точка x для рассмотрения, предком которой является p(x); направление движение от p(x) к x является прямолинейное перемещение вправо.
(Левая картинка): Рекурсивно применяем правило отсечки и получаем у в качестве преемника прыжковой точки х. Эта точка интересна тем, что есть сосед z, в который можно попасть по оптимальному пути только через y. Промежуточные точки не генерируются и не рассматриваются.
(Правая картинка): Рекурсивно принимаем диагональные правила отсечки. Обратите внимание, что перед каждым следующим диагональным шагом необходимо рекурсивно пройтись по прямым линиям (выделены пунктиром). Только если обе “прямые” рекурсии не могут определить точку следующего прыжка, то перемещаемся дальше по диагонали. Точка w – вынужденный сосед х, создаётся как обычный.
Далее опишем, каким образом отсекать множество точек, непосредственно примыкающих к некоторой точке х. Цель заключается в нахождении таких соседей, т.е. neighbours(x), до любых n точек которых нельзя достичь цель оптимально. Мы добиваемся этого путём сравнения двух путей: p, который начинается точкой p(x), посещает x и заканчивается c n и другим путём p’, который так же начинается с p(x), посещает x и заканчивается n, но не содержат х. Кроме того, каждая точка, содержащаяся в p или p’, должна относиться к neighbours(x).
Есть два случая, в зависимости от того, какой переход к х происходит из p(x): прямой ход или диагональный. Стоит учесть, что если x является началом p(x), то p(x) пусто и отсечение не происходит.
Прямые переходы:
Отсекаются любые точки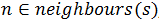 , которые удовлетворяют следующему утверждению:
, которые удовлетворяют следующему утверждению:
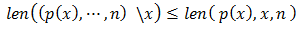 (1)
(1)
 а
а
Здесь p(x) = 4 и мы отсекаем всех соседей кроме n = 5
Диагональные переходы:
Здесь отличия в том, что путь, который исключает х, должен быть строго доминирующим:
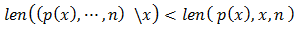 (2)
(2)
 б
б
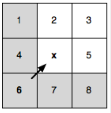
Здесь p(x) = 6 и отсекаются все соседи, кроме n = 2, n = 3 и n = 5.
Предполагая, что neighbours(x) не содержат препятствий, будем ссылаться на точки, которые остаются после прямой или диагональной отсечки (при необходимости), как естественные соседи x. Они соответствуют не серым точкам на а и б рисунках. Когда neighbours(x) содержат препятствия, нельзя отсечь всех не естественных соседей. В этом случае такой сосед считается принуждённым (искусственным).
Определение 1.
Точка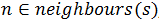 является принуждённой, если
является принуждённой, если
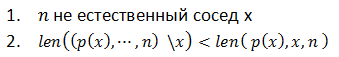
 в
в
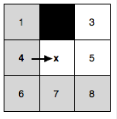
На примере в показан прямой переход, где n = 3 — принуждённый.
 г
г
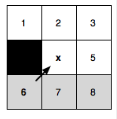
На примере г показан пример диагонального перемещения; здесь n=1 – принуждённый сосед.
Введём определение:
Определение 2.
Точка y является точкой прыжка точки х, в направлении d, если y минимизирует значение k так, что y = x + kd, и выполняется одно из следующих условий:

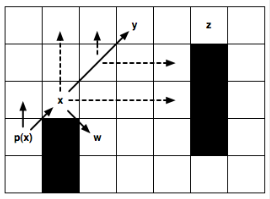
Этот рисунок показывает пример точки прыжка, которая определена условием 3. Здесь мы начинаем в точке х и заканчиваем движение по диагонали, пока не наткнёмся на точку у. Из у в точку z можно попасть с kiшагами по горизонтали. Таким образом, z является преемником точки для прыжка x (по условию 2), а это в свою очередь определяет y как преемник для прыжка точки x.
Алгоритм 1. Определение преемника.
Зададим: х – текущая точка, s – начало, g – цель
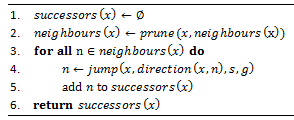
Алгоритм 1 показывает как искать преемника для текущей точки. Сначала обрезается множество соседей, непосредственно примыкающих к текущей точке х (строка 2). Тогда вместо добавления каждого соседа n в множество successors (преемников) для x, попробуем “перепрыгнуть” к точке, которая находится дальше, но которая лежит относительно направлению x к n (строки 3-5). Например, если ребро (x; n) представляет собой движение по прямой вправо от x, то смотрим точку прыжка непосредственно справа от x. Если находится такая точка, то она добавляется в набор преемников вместо n. Если до точки прыжка дойти не получается, то ничего не добавляется. Процесс продолжается до тех пор, пока все соседи не закончатся, и затем алгоритм вернёт список всех преемников для х (строка 6).
Алгоритм 2. Функция прыжка.
Зададим: х – точка отчёта, d – направление, s – начало, g – цель

Для того, чтобы найти отдельных преемников для точки прыжка, воспользуемся алгоритмом 2. Он требует точки отчёта x, направление движения d, а так же начальную точку s и целевую точку g. Алгоритм пытается установить, имеет ли x точку для прыжка среди преемников, перемещаясь по направлению d (строка 1) и проверяет, удовлетворяет ли точка n Определению 2. В этом случае, n обозначается точкой прыжка и возвращается (строки 5, 7 и 11). Если n не является точкой прыжка, алгоритм рекурсивно повторяется и двигается снова в направлении d, но в этот раз n – новая точка отчёта (строка 12). Рекурсия прекращается, когда встречается препятствие и никакие дальнейшие действия не могут быть предприняты (строка 3). Стоит обратить внимание, что перед каждым диагональным шагом алгоритм должен обнаружить точки прыжка по прямым направлениям (строки 9-11). Эта проверка соответствует третьему условию Определения 2 и имеет важное значение для сохранения оптимальности алгоритма.
Описание алгоритма в оригинале: harablog.wordpress.com/2011/09/07/jump-point-search
Реализация на js: qiao.github.com/PathFinding.js/visual (выбрать Jump Point Search и расставить стенки)
Сам код на js: github.com/qiao/PathFinding.js/blob/master/src/finders/JumpPointFinder.js
Benchmark: github.com/Yonaba/Jumper-Benchmark
Подробный визуализатор: zerowidth.com/2013/05/05/jump-point-search-explained.html
Терминология и обозначения
Алгоритм работает на неориентированном графе единой стоимости. Каждое поле карты имеет <= 8 соседей, которые могут быть проходимы или же нет. Каждый шаг по направлению (по вертикали или по горизонтали) имеет стоимость 1; шаг по диагонали имеет стоимость √2. Движения через препятствия запрещены. Обозначение относится к одному из восьми направлений движения (вверх, вниз, влево и т.д.).
- Запись y = x + kd означает, что точка y может быть достигнута через k шагов из x в направлении d. Когда d – движение по диагонали, перемещение делится на два перемещения по прямой d1 и d2.
- Путь p = (n0, n1, …, nk) – упорядоченное перемещение по точкам без циклов из точки n0 до точки nk.
- Обозначение p \ x означает, что точка x не встречается на пути p.
- Обозначение len(p) означает длину или стоимость пути p.
- Обозначение dist(x, y) означает длину или стоимость пути между точками x и y.
Jump points
“Прыжковые точки” позволяют ускорить алгоритм поиска пути, рассматривая только “необходимые” точки. Такие точки могут быть описаны двумя простыми правилами выбора соседей при рекурсивном поиске: одно правило для прямолинейного движения и другое – для диагонального. В обоих случаях необходимо доказать, что исключая из набора ближайших соседей вокруг точки, найдётся оптимальный путь из предка текущей точки до каждого из соседей, и этот путь не будет содержать в себе посещенную точку. Рассмотрим случай 1, который отражает основную идею:
Случай 1: Отсечённый сосед

Х – текущая рассматриваемая точка. Стрелка указывает направление движения. И там и там можно сразу отсечь соседей, выделенных серым, т.к. туда можно попасть по оптимальному пути из p(x), никогда не проходя через x.
Будем ссылаться на множество точек, которые остаются после отсечения настоящих соседей текущей точки. Они отмечены белыми на рисунке. В идеале, мы хотим учитывать только настоящих соседей во время просмотра. Тем не менее, в некоторых случаях, наличие препятствий может означать, что мы должны также рассмотреть небольшой набор до K дополнительных точек (0 ≤ K ≤ 2). Мы говорим, что это точки вынужденных соседей текущей позиции.
Случай 2: Принуждённый сосед

Х – текущая рассматриваемая точка. Стрелка указывает направление движения. Обратите внимание, что, когда х находится рядом с препятствием, выделенные соседи не могут быть отсечены, любой альтернативный оптимальный путь от p(х) в каждом из этих узлов, блокируется.
Эти случаи применяются следующим образом: вместо создания “вынужденных” и “естественных” соседей мы рекурсивно отсекаем список соседей вокруг каждой точки. Таким образом наша цель заключается в ликвидации “симметрии”, рекурсивно “перепрыгивая” через все точки, в которые можно попасть по оптимальному пути, который не проходил через текущую позицию. Рекурсия останавливается при попадании на препятствие или нашли так называемую “прыжковую точку-преемник” (jump point successor). Прыжковые точки интересны тем, что они имеют соседей, которые не могут быть достигнуты альтернативным путём: оптимальный путь должен идти через текущую точку. Таким образом g(y) = g(x) + dist(x; y) – стоимость перемещения.
Для обеспечения оптимальности необходимо только определиться как выбирать соседей (сначала линейные, затем диагональные).
Рассмотрим пример:

Здесь добавляется точка x для рассмотрения, предком которой является p(x); направление движение от p(x) к x является прямолинейное перемещение вправо.
(Левая картинка): Рекурсивно применяем правило отсечки и получаем у в качестве преемника прыжковой точки х. Эта точка интересна тем, что есть сосед z, в который можно попасть по оптимальному пути только через y. Промежуточные точки не генерируются и не рассматриваются.
(Правая картинка): Рекурсивно принимаем диагональные правила отсечки. Обратите внимание, что перед каждым следующим диагональным шагом необходимо рекурсивно пройтись по прямым линиям (выделены пунктиром). Только если обе “прямые” рекурсии не могут определить точку следующего прыжка, то перемещаемся дальше по диагонали. Точка w – вынужденный сосед х, создаётся как обычный.
Правила отсечения соседа
Далее опишем, каким образом отсекать множество точек, непосредственно примыкающих к некоторой точке х. Цель заключается в нахождении таких соседей, т.е. neighbours(x), до любых n точек которых нельзя достичь цель оптимально. Мы добиваемся этого путём сравнения двух путей: p, который начинается точкой p(x), посещает x и заканчивается c n и другим путём p’, который так же начинается с p(x), посещает x и заканчивается n, но не содержат х. Кроме того, каждая точка, содержащаяся в p или p’, должна относиться к neighbours(x).
Есть два случая, в зависимости от того, какой переход к х происходит из p(x): прямой ход или диагональный. Стоит учесть, что если x является началом p(x), то p(x) пусто и отсечение не происходит.
Прямые переходы:
Отсекаются любые точки
 , которые удовлетворяют следующему утверждению:
, которые удовлетворяют следующему утверждению: (1)
(1) а
аЗдесь p(x) = 4 и мы отсекаем всех соседей кроме n = 5
Диагональные переходы:
Здесь отличия в том, что путь, который исключает х, должен быть строго доминирующим:
 (2)
(2) б
бЗдесь p(x) = 6 и отсекаются все соседи, кроме n = 2, n = 3 и n = 5.
Предполагая, что neighbours(x) не содержат препятствий, будем ссылаться на точки, которые остаются после прямой или диагональной отсечки (при необходимости), как естественные соседи x. Они соответствуют не серым точкам на а и б рисунках. Когда neighbours(x) содержат препятствия, нельзя отсечь всех не естественных соседей. В этом случае такой сосед считается принуждённым (искусственным).
Определение 1.
Точка
 является принуждённой, если
является принуждённой, если
 в
вНа примере в показан прямой переход, где n = 3 — принуждённый.
 г
гНа примере г показан пример диагонального перемещения; здесь n=1 – принуждённый сосед.
Описание алгоритма
Введём определение:
Определение 2.
Точка y является точкой прыжка точки х, в направлении d, если y минимизирует значение k так, что y = x + kd, и выполняется одно из следующих условий:
- Точка y – точка назначения.
- У точки y есть хотя бы один сосед, который является принуждённым по определению 1.
- d – движение по диагонали и существует точка z = y + kidi, которая лежит в ki шагах в направлении di ∈ {d1, d2}, таких что z – точка прыжка из y при условии 1 или 2.

Этот рисунок показывает пример точки прыжка, которая определена условием 3. Здесь мы начинаем в точке х и заканчиваем движение по диагонали, пока не наткнёмся на точку у. Из у в точку z можно попасть с kiшагами по горизонтали. Таким образом, z является преемником точки для прыжка x (по условию 2), а это в свою очередь определяет y как преемник для прыжка точки x.
Алгоритм 1. Определение преемника.
Зададим: х – текущая точка, s – начало, g – цель

Алгоритм 1 показывает как искать преемника для текущей точки. Сначала обрезается множество соседей, непосредственно примыкающих к текущей точке х (строка 2). Тогда вместо добавления каждого соседа n в множество successors (преемников) для x, попробуем “перепрыгнуть” к точке, которая находится дальше, но которая лежит относительно направлению x к n (строки 3-5). Например, если ребро (x; n) представляет собой движение по прямой вправо от x, то смотрим точку прыжка непосредственно справа от x. Если находится такая точка, то она добавляется в набор преемников вместо n. Если до точки прыжка дойти не получается, то ничего не добавляется. Процесс продолжается до тех пор, пока все соседи не закончатся, и затем алгоритм вернёт список всех преемников для х (строка 6).
Алгоритм 2. Функция прыжка.
Зададим: х – точка отчёта, d – направление, s – начало, g – цель

Для того, чтобы найти отдельных преемников для точки прыжка, воспользуемся алгоритмом 2. Он требует точки отчёта x, направление движения d, а так же начальную точку s и целевую точку g. Алгоритм пытается установить, имеет ли x точку для прыжка среди преемников, перемещаясь по направлению d (строка 1) и проверяет, удовлетворяет ли точка n Определению 2. В этом случае, n обозначается точкой прыжка и возвращается (строки 5, 7 и 11). Если n не является точкой прыжка, алгоритм рекурсивно повторяется и двигается снова в направлении d, но в этот раз n – новая точка отчёта (строка 12). Рекурсия прекращается, когда встречается препятствие и никакие дальнейшие действия не могут быть предприняты (строка 3). Стоит обратить внимание, что перед каждым диагональным шагом алгоритм должен обнаружить точки прыжка по прямым направлениям (строки 9-11). Эта проверка соответствует третьему условию Определения 2 и имеет важное значение для сохранения оптимальности алгоритма.
Ссылки
Описание алгоритма в оригинале: harablog.wordpress.com/2011/09/07/jump-point-search
Реализация на js: qiao.github.com/PathFinding.js/visual (выбрать Jump Point Search и расставить стенки)
Сам код на js: github.com/qiao/PathFinding.js/blob/master/src/finders/JumpPointFinder.js
Benchmark: github.com/Yonaba/Jumper-Benchmark
Подробный визуализатор: zerowidth.com/2013/05/05/jump-point-search-explained.html