Доброго времени суток, хабражители!
Мне очень нравятся барочные элементы. В очередной раз встретив подобный узор на одном из сайтов, представил, как бы он чудесно смотрелся в анимации, картинка бы ожила. Тем более с приходом html5 оживление должно стать гораздо проще в реализации. Но как по точкам нарисовать кривую? Тут как раз кстати вспомнилась кривая Безье!
На уроках векторной графики я люто ненавидел кривые Безье. Принцип ее работы казался магическим, непостижимым и, как бы не сказать грубее, нелогичным. Складывалось ощущение, что сама кривая не знает как извернуться, и как наглый котяра растягивалась как ей удобнее, а не как мне надо.
На самом деле, как всегда, надо было лишь уделить немного времени теории. Все оказалось просто и довольно интересно. В итоге получилась реализация кривых на яваскрипте с использованием canvas.
Кому интересно как строится эта извилистая бестия добро пожаловать под кат!
Начнем с принципа построения. Кривая Безье строится по нескольким опорным точкам. Образно говоря: кривая начинается в нулевой опорной точке, начинает двигаться к первой, но вдруг замечает вторую — начинает тяготеть к ней, плавно меняет свой маршрут в ее сторону, а тут на горизонте появляется третья, еще более привлекательная… И так пройдя стороной мимо всех точек, кривая останавливает свой выбор на последней опорной точке, куда и приходит. Путь получается как у алкоголика идущего под утро домой.

От лирики перейдем к суровой математике.
Теория нагло заимствована из Википедии:
Кривая Безье является частным случаем многочленов Бернштейна, представляет собой параметрическую кривую и задаётся выражением:
 , где
, где
n — количество опорных точек;
i — номер опорной точки;
t — шаг на котором мы считаем положение кривой. К примеру, при построении кривой по 100 точкам, шаг будет 0,01 (не опорным, а точкам на самой кривой);
Р — в нашем случае координата опорной точки;
b(t) — базисная функция кривой Безье. Этот коэффициент, определяет вес опорной точки. Является собственно полином Бернштейна:

, где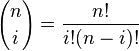 — число сочетаний из n по i, где n — степень полинома, i — порядковый номер опорной вершины.
— число сочетаний из n по i, где n — степень полинома, i — порядковый номер опорной вершины.
На первом и последнем шагах значение полинома Бернштейна равно 1, объяснение здесь. На середину кривой наибольшее влияние оказывают средние опорные точки, в первой трети — опорные точки первой трети и так далее. Полином Бернштейна принимает значения от 0 до 1.
И так, чтобы посчитать координату кривой Безье нам надо:
С теорией вроде разобрались, переходим к практике.
Считаем базисную функцию:
Далее получаем координаты кривой.
Построить кривую Безье можно в трехмерном, четырехмерном пространстве и так далее, но мы остановимся на плоскости.
Рисуем кривую:
Пора пробовать:
Пример на jsfiddle
Ссылки по теме:
Статья на javascript.ru
upd: Стандарт HTML5 поддерживает методы quadraticCurveTo и bezierCurveTo для построения кривых Безье по трем и четырем точкам соответственно. Спасибо lany.
Мне очень нравятся барочные элементы. В очередной раз встретив подобный узор на одном из сайтов, представил, как бы он чудесно смотрелся в анимации, картинка бы ожила. Тем более с приходом html5 оживление должно стать гораздо проще в реализации. Но как по точкам нарисовать кривую? Тут как раз кстати вспомнилась кривая Безье!
На уроках векторной графики я люто ненавидел кривые Безье. Принцип ее работы казался магическим, непостижимым и, как бы не сказать грубее, нелогичным. Складывалось ощущение, что сама кривая не знает как извернуться, и как наглый котяра растягивалась как ей удобнее, а не как мне надо.
На самом деле, как всегда, надо было лишь уделить немного времени теории. Все оказалось просто и довольно интересно. В итоге получилась реализация кривых на яваскрипте с использованием canvas.
Кому интересно как строится эта извилистая бестия добро пожаловать под кат!
Немного теории
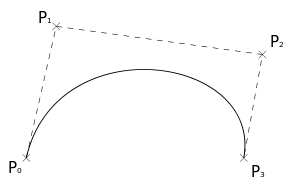
Начнем с принципа построения. Кривая Безье строится по нескольким опорным точкам. Образно говоря: кривая начинается в нулевой опорной точке, начинает двигаться к первой, но вдруг замечает вторую — начинает тяготеть к ней, плавно меняет свой маршрут в ее сторону, а тут на горизонте появляется третья, еще более привлекательная… И так пройдя стороной мимо всех точек, кривая останавливает свой выбор на последней опорной точке, куда и приходит. Путь получается как у алкоголика идущего под утро домой.
От лирики перейдем к суровой математике.
Теория нагло заимствована из Википедии:
Кривая Безье является частным случаем многочленов Бернштейна, представляет собой параметрическую кривую и задаётся выражением:
 , где
, где n — количество опорных точек;
i — номер опорной точки;
t — шаг на котором мы считаем положение кривой. К примеру, при построении кривой по 100 точкам, шаг будет 0,01 (не опорным, а точкам на самой кривой);
Р — в нашем случае координата опорной точки;
b(t) — базисная функция кривой Безье. Этот коэффициент, определяет вес опорной точки. Является собственно полином Бернштейна:

, где
 — число сочетаний из n по i, где n — степень полинома, i — порядковый номер опорной вершины.
— число сочетаний из n по i, где n — степень полинома, i — порядковый номер опорной вершины.На первом и последнем шагах значение полинома Бернштейна равно 1, объяснение здесь. На середину кривой наибольшее влияние оказывают средние опорные точки, в первой трети — опорные точки первой трети и так далее. Полином Бернштейна принимает значения от 0 до 1.
И так, чтобы посчитать координату кривой Безье нам надо:
- Посчитать вес опорной точки;
- Умножить вес на координату этой опорной точки;
- Повторить шаги 1-2 для всех опорных точек;
- Сложить получившиеся значения — это и будет координата кривой.
С теорией вроде разобрались, переходим к практике.
Ура! Практика.
Считаем базисную функцию:
// i - номер вершины, n - количество вершин, t - положение кривой (от 0 до 1)
function getBezierBasis(i, n, t) {
// Факториал
function f(n) {
return (n <= 1) ? 1 : n * f(n - 1);
};
// считаем i-й элемент полинома Берштейна
return (f(n)/(f(i)*f(n - i)))* Math.pow(t, i)*Math.pow(1 - t, n - i);
}
Далее получаем координаты кривой.
Построить кривую Безье можно в трехмерном, четырехмерном пространстве и так далее, но мы остановимся на плоскости.
// arr - массив опорных точек. Точка - двухэлементный массив, (x = arr[0], y = arr[1])
// step - шаг при расчете кривой (0 < step < 1), по умолчанию 0.01
function getBezierCurve(arr, step) {
if (step == undefined) {
step = 0.01;
}
var res = new Array()
for (var t = 0; t < 1 + step; t += step) {
if (t > 1) {
t = 1;
}
var ind = res.length;
res[ind] = new Array(0, 0);
for (var i = 0; i < arr.length; i++) {
var b = getBezierBasis(i, arr.length - 1, t);
res[ind][0] += arr[i][0] * b;
res[ind][1] += arr[i][1] * b;
}
}
return res;
}
Рисуем кривую:
// ctx - rendering context холста, arr - массив точек по которым строим кривую
// delay - задержка перед отрисовкой следующей точки, pause - пауза перед началом рисования,
function drawLines(ctx, arr, delay, pause) {
if (delay == undefined) {
delay = 10;
}
if (pause == undefined) {
pause = delay;
}
var i = 0;
function delayDraw() {
if (i >= arr.length - 1) {
return;
}
ctx.moveTo(arr[i][0],arr[i][1]);
ctx.lineTo(arr[i+1][0],arr[i+1][1]);
ctx.stroke();
++i;
setTimeout(delayDraw, delay);
}
setTimeout(delayDraw, pause);
}
Пора пробовать:
drawC = document.getElementById('bezier');
drawC.width = document.width - 30;
drawC.height = document.height - 30;
if (drawC && drawC.getContext) {
ctx = drawC.getContext('2d');
ctx.fillStyle="#33CC99";
ctx.lineWidth=0.1;
var flow; // Массив координат кривой
var arr = new Array();
arr[0] = new Array(0, 100);
arr[1] = new Array(100, 80);
arr[2] = new Array(150, 150);
arr[3] = new Array(200, 155);
flow = getBezierCurve(new Array(arr[0], arr[1], arr[2], arr[3]), 0.01);
drawLines(ctx, flow, 10);
}
Пример на jsfiddle
Ссылки по теме:
Статья на javascript.ru
upd: Стандарт HTML5 поддерживает методы quadraticCurveTo и bezierCurveTo для построения кривых Безье по трем и четырем точкам соответственно. Спасибо lany.